Z-order vs R-tree, оптимизация и 3D

Ранее (1, 2) мы обосновали и продемонстрировали возможность существования
пространственного индекса, обладающего всеми плюсами обычного B-Tree — индекса и
не уступающего по производительности индексу на основе R-Tree.
Под катом обобщение алгоритма на трёхмерное пространство, оптимизации и бенчмарки.
3D
Зачем вообще нужен этот 3D? Дело в том, что мы живём в трёхмерном мире. Поэтому данные представлены либо в гео-координатах (latitude, longitude) и тогда искажены тем более, чем дальше они от экватора. Либо к ним прилагается проекция, которая адекватна только на определенном пространстве этих координат. Трехмерный индекс позволяет расположить точки на сфере и избежать тем самым существенных искажений. Для получения поискового экстента достаточно определить на сфере центр искомого куба и отступить в стороны по всем координатам на радиус.
Принципиально трёхмерный вариант алгоритма ничем от двухмерного не отличается — разница лишь в работе с ключом:
- чередование разрядов в ключе идет теперь с шагом 3, а не 2 т.е. …z1y1×1z0y0×0
- в ключе теперь 96, а не 64 разряда. Вариант разместить всё в 64-разрядном ключе отвергнут т.к. дает всего 21 разряд на координату, что сделало бы нас немного скованными. Кроме того грядут 4 и 6 мерные ключи (угадайте зачем), а уж там 64 не хватит никак, так зачем оттягивать неизбежное. К счастью, это не так уж и сложно
- следовательно, ключ теперь не bigint, а numeric и в интерфейсе ключа потребуются методы перевода из numeric и обратно
- изменятся методы получения ключа из координат и обратно
- а так же метод расщепления подзапроса. Напомним, для расщепления запроса, который представлен двумя ключами, соответствующими левому нижнему и правому верхнему его углам мы:
- находили в них самый старший различающийся бит m
- правый верхний угол меньшего нового подзапроса получается выставлением в 1 всех битов соответствующей m координаты младше m
- левый нижний угол большего нового подзапроса получается выставлением в 0 всех битов соответствующей m координаты младше m
Numeric
Сам numeric нам напрямую недоступен из extension. Приходится пользоваться универсальным механизмом вызова функций с маршаллингом — DirectFunctionCall[X] из «include/fmgr.h», где X — число аргументов.
Внутри numeric устроен как массив short, каждый из которых содержит 4 десятичные цифры — от 0 до 9999. В его интерфейсе нет сдвигов или деления с возвратом модуля. Равно как и специальных функций для работы со степенями 2 (при таком устройстве они и не к месту). Поэтому, чтобы разобрать numeric на два int64 приходится действовать так:
void bit3Key_fromLong(bitKey_t *pk, Datum dt)
{
Datum divisor_numeric;
Datum divisor_int64;
Datum low_result;
Datum upper_result;
divisor_int64 = Int64GetDatum((int64) (1ULL << 48));
divisor_numeric = DirectFunctionCall1(int8_numeric, divisor_int64);
low_result = DirectFunctionCall2(numeric_mod, dt, divisor_numeric);
upper_result = DirectFunctionCall2(numeric_div_trunc, dt, divisor_numeric);
pk->vals_[0] = DatumGetInt64(DirectFunctionCall1(numeric_int8, low_result));
pk->vals_[1] = DatumGetInt64(DirectFunctionCall1(numeric_int8, upper_result));
pk->vals_[0] |= (pk->vals_[1] & 0xffff) << 48;
pk->vals_[1] >>= 16;
}А для обратного преобразования — так:
Datum bit3Key_toLong(const bitKey_t *pk)
{
uint64 lo = pk->vals_[0] & 0xffffffffffff;
uint64 hi = (pk->vals_[0] >> 48) | (pk->vals_[1] << 16);
uint64 mul = 1ULL << 48;
Datum low_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(lo));
Datum upper_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(hi));
Datum mul_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(mul));
Datum nm = DirectFunctionCall2(numeric_mul, mul_result, upper_result);
return DirectFunctionCall2(numeric_add, nm, low_result);
}Работа с арифметикой произвольной точности вообще вещь не быстрая, тем более когда речь заходит о делениях. Поэтому у автора возникло непреодолимое желание «хакнуть» numeric и разобрать его самостоятельно. Пришлось продублировать локально определения из numeric.c и обрабатывать сырые short«ы. Это было несложно и ускорило работу в десятки раз.
Сплошные подзапросы.
Как мы помним, алгоритм расщепляет подзапросы до тех пор, пока лежащие под ним данные полностью не уместятся на одной дисковой странице. Происходит это так:
- на входе подзапрос, у него есть интервал значений между левым нижним (ближним) и правым верхним (дальним) углами. Координат стало больше, но суть та же
- делаем поиск в BTree по ключу меньшего угла
- добираемся при этом до листовой страницы и проверяем ее последнее значение
- если последнее значение >= значения ключа большего угла, просматриваем всю страницу и заносим в выдачу всё, что попало в поисковый экстент
- если меньше, продолжаем расщеплять запрос
Однако, может так случиться, что подзапрос, данные для которого содержатся на десятках или сотнях страниц полностью расположен внутри исходного поискового экстента. Нет никакого смысла резать его дальше, данные из интервала можно смело без всяких проверок вносить в результат.
Как же распознать такой подзапрос? Довольно просто —
- его размеры по всем координатам должны быть степенями 2 и равны (куб)
- углы должны лежать на соответствующей решетке с шагом в ту же степень 2
Вот так выглядит карта подзапросов до оптимизации кубами:

А вот так после: 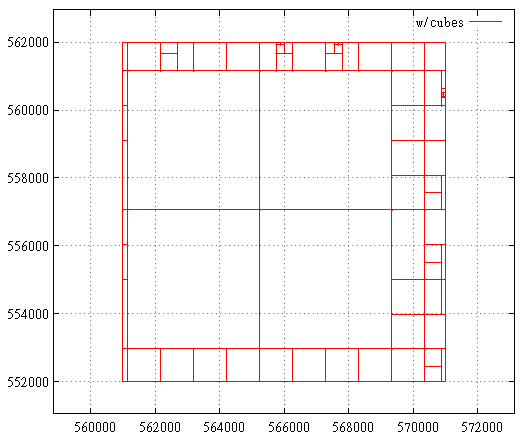
Benchmark
В таблицу сведены сравнительные результаты работы исходного алгоритма, оптимизированного его варианта и GiST R-Tree.
R-Tree двумерное, для сравнения в z-индекс вносились псевдо-3D данные, т.е. (x, 0, z). С точки зрения алгоритма никакой разницы нет, мы всего-лишь даем R-дереву некоторую фору.
Данные — 100 000 000 случайных точек в [0…1 000 000, 0…0, 0…1 000 000].
Замеры проводились на скромной виртуальной машине с двумя ядрами и 4 Гб ОЗУ, поэтому времена не имеют абсолютной ценности, а вот числам прочитанных страниц по прежнему можно доверять.
Времена показаны на вторых прогонах, на разогретом сервере и виртуальной машине. Количества прочитанных буферов — на свеже-поднятом сервере.
| Npoints | Nreq | Type | Time (ms) | Reads | Hits |
|---|---|---|---|---|---|
| 1 | 100 000 | старый новый rtree |
.37 .36 .38 |
1.13154 1.13307 1.83092 |
3.90815 3.89143 3.84164 |
| 10 | 100 000 | старый новый rtree |
.40 .38 .46 |
1.55 1.57692 2.73515 |
8.26421 7.96261 4.35017 |
| 100 | 100 000 | старый новый rtree (*) |
.63 .48 .50… 7.1 |
3.16749 3.30305 6.2594 |
45.598 31.0239 4.9118 |
| 1 000 | 100 000 | старый новый rtree (*) |
2.7 1.2 1.1… 16 |
11.0775 13.0646 24.38 |
381.854 165.853 7.89025 |
| 10 000 | 10 000 | старый новый rtree (*) |
22.3 5.5 4.2… 135 |
59.1605 65.1069 150.579 |
3606.73 651.405 27.2181 |
| 100 000 | 10 000 | старый новый rtree (*) |
199 53.3 35…1200 |
430.012 442.628 1243.64 |
34835.1 2198.11 186.457 |
| 1 000 000 | 1 000 | старый новый rtree (*) |
2550 390 300… 10000 |
3523.11 3629.49 11394 |
322776 6792.26 3175.36 |
Npoints — среднее число точек в выдаче
Nreq — число запросов в серии
Type — «старый» — исходный вариант,
«новый» — с оптимизацией numeric и сплошными подзапросами;
«rtree»- gist only 2D rtree,
(*) — для того, чтобы сравнить время поиска,
приходилось уменьшать серию в 10 раз,
иначе страницы не умещались в кэш
Time (ms) — среднее время выполнения запроса
Reads — среднее число чтений на запрос
Hits — число обращений к буферам
В виде графиков эти данные выглядят так:
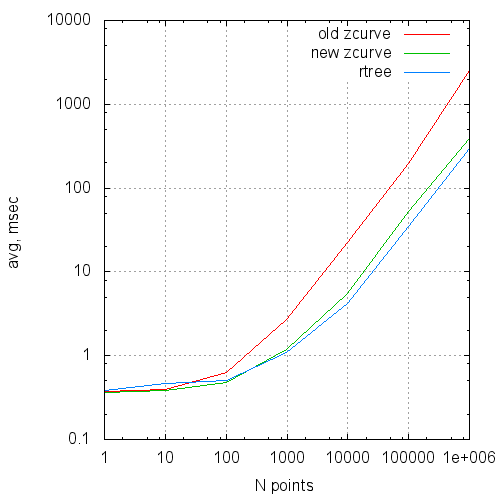
Среднее время выполнения запроса от размера запроса

Среднее число чтений на запрос от размера запроса
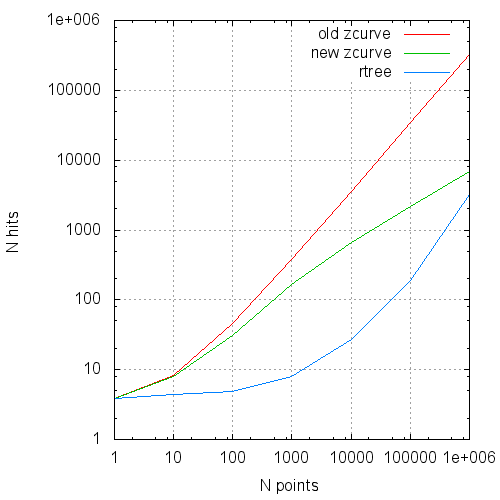
Среднее число обращений к кэшу страниц на запрос от размера запроса
Выводы
Пока всё неплохо. Продолжаем двигаться в направлении использовании для пространственной индексации кривой Гильберта, а так же полноценных замеров на несинтетических данных.
PS: описанные изменения доступны здесь.
