Вычисление коэффициентов прохождения и отражения для плоской волны, падающей на стопку пластин05.05.2017 03:21

Есть стопка стеклянных пластинок и захотелось нам построить для этой стопки частотную характеристику пропускания (или отражения) света. Вот как на рисунке: берем две стеклянные пластинки (отличаются показателем преломления) — строим; потом собираем стопочку из 10 пластин (те же два показателя преломления чередуются) — опять строим;, а в конце делаем стопочку потолще (из 50 пластин) — и снова строим. Интересная же картинка: для толстой стопки есть интервал частот, которые совсем не проходят, Т=0, — вот эта стопка называется «одномерный фотонный кристалл».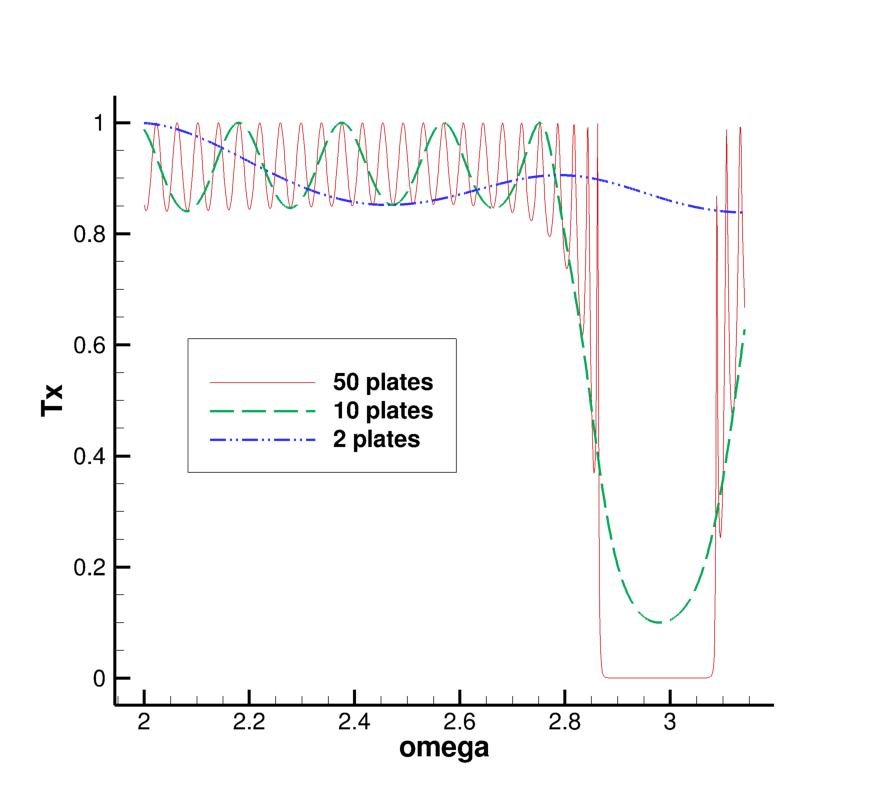
Ну, а как строить-то такую характеристику? А если пластинки поглощающие? А вдруг они еще и анизотропные некоторые? А если не просто анизотропные, а прям холестерические, как в жидкокристаллических мониторах? А если все они вообще разные и каждая со своим дихроизмом? Не беда!

Статья ориентирована на тех, кто захочет написать код функции, поэтому без математических выкладок — всё в стиле «делай, не думай».

Постановка задачи

Отрезок $z \in [0,L]$ разделен на $n$ частей — «одномерных анизотропных пластин холестерического типа». Каждая пластина имеет свой собственный набор параметров: $\varepsilon_{\perp, i}$ , $\varepsilon_{\parallel, i}$ , $\mu_{\parallel, i}$ , $\mu_{\perp, i}$ , $q_i$ , $\varphi_{0, i}$ , а также толщину $$d_i>0:\sum^{n}_{i=1}d_i=L$» />. Номера пластин упорядочены в порядке следования одной за другой слева направо (вдоль возрастания координаты <img src=$ ). Слева и справа от стопки анизотропных пластин находятся изотропные среды с параметрами: $\varepsilon_{0},\mu_{0}$ при $z<0$ и $\varepsilon_{L},\mu_{L}$ при $z>L$» />. Слева на стопку пластин падает плоская электромагнитная волна с частотой <img src= . Требуется найти коэффициент отражения $R$ и коэффициент пропускания $T$ .

Задача решается в безразмерных величинах. Параметр обезразмеривания $r^*_{sgs}$ выбирается исходя из удобства. Безразмерные величины выражаются через размерные в системе $SGS$ следующим образом:

$\vec{r}=\vec{r}_{sgs}/r^*_{sgs},\quad t=t_{sgs}\cdot c_{sgs}/r^*_{sgs},\quad\omega =\omega_{sgs}\cdot r^*_{sgs}/c_{sgs},\quad\sigma=\sigma_{sgs}\cdot 4\pi r^*_{sgs}/c_{sgs},\quad q=q_{sgs}\cdot r^*_{sgs}.$

При обезразмеривании вещественные части величин $\varepsilon,\, \mu$ не изменяются.
Аргументы (уже обезразмеренные)

$\varepsilon_{0}$ , $\mu_{0}$ — диэлектрическая и магнитная проницаемости крайней левой изотропной среды (не обязательно вакуум, индекс значит $z=0$ ),
$\varepsilon_{L}$ , $\mu_{L}$ — диэлектрическая и магнитная проницаемости крайней правой изотропной среды (индекс: $z=L$ ),
$\omega$ — частота падающей волны,

Далее для каждого $i$ -слоя (всего $n\in N$ слоев):

$d_i>0$» /> — толщина слоя, <br /><img src= — пространственная частота холестерической спирали (может принимать отрицательные значения),
$\varphi_{0, i}$ — «начальный» (какой он был бы при $z=0$ , если спираль продолжить назад, — невзирая на истинную начальную координату $i$ -слоя) угол между осью $O_x$ и вектором-директором $\textbf{n}$ (см рис. ниже),
$\varepsilon_{\perp, i}$ , $\varepsilon_{\parallel, i}$ , $\mu_{\parallel, i}$ , $\mu_{\perp, i}\in C$ — в общем случае комплексные продольные и поперечные диэлектрические и магнитные проницаемости.

При этом мнимые части диэлектрических и магнитных проницаемостей отвечают за поглощение: $Im(\varepsilon_{\perp})=-{\sigma_{\perp}}/{\omega}$ , $Im(\varepsilon_{\parallel})=-{\sigma_{\parallel}}/{\omega}$ , $Im(\mu_{\perp})=-{\sigma^*_{\perp}}/{\omega}$ , $Im(\mu_{\parallel})=-{\sigma^*_{\parallel}}/{\omega}$ .

Возвращаемые значения

Всего рассматривается 4 типа падающих волн:

плоская поляризация по ,
плоская поляризация по ,
круговая поляризация правая ,
круговая поляризация левая .

В соответствии с типом падающей волны, функция возвращает 4 коэффициента пропускания и 4 коэффициента отражения (всего 8 значений): $R_x, T_x, R_y, T_y, R_l, T_l, R_r, T_r$ .

Коэффициенты определяются как доли энергии (отраженной, пропущенной) от энергии падающей волны.

При желании, долю поглощенной энергии $A$ в стопке можно вычислить по формуле: $A_{\alpha}=1-(R_{\alpha} + T_{\alpha})$ , где индекс $\alpha$ обозначает тип падающей волны: $x,y,r,l$ .

В основном действия состоят из вычисления и произведения комплексных матриц размерностью $4\times4$ .

Для обозначения каждой матрицы используется открывающая скобка, буква и закрывающая скобка. Например: $[z),~(\beta\},~\{z\rangle$ . Открывающая и закрывающая скобки не всегда одинаковы. Обратные матрицы обозначаются обратным порядком скобок, например: $\{z\rangle:=\langle z\}^{-1}$ . Буквой $z$ в скобках подчеркивается зависимость марицы от координаты. Если матрица не зависит от координаты, то в скобках присутствует другая буква. Таким образом, при обозначении матрицы, значение имеет уникальный набор скобок и их порядок следования.

Обозначения используются для лаконичности записи произведения матриц и удобства проверки правильности записи, выражаемого мнемоническим правилом: соседние перемножаемые матрицы должны иметь одинаковые граничащие скобки, что имеет смысл при переходе из одного пространства в другое. Эти-то 4-мерные пространства и обозначаются скобками: $]$ — пространство «неподвижное декартово», $)$ — пространство «вращающееся декартово», $\}$ — пространство «собственных векторов», $\rangle$ — пространство «количеств и направлений волн». Произведение матрицы на вектор интерпретируется как новое представление вектора: или в другом 4-пространстве, но при той же координате (если скобки матрицы отличаются) или в другой координате, но в том же 4-пространстве (если открывающя и закрывающая скобки одинаковы).

Для каждого слоя вычисляются 4 собственных значения по формуле:

$\lambda=\pm i \sqrt{\eta\pm\tau},$

где

$\eta = \frac{\omega^2}{2}(\varepsilon_{\perp}\mu_{\parallel}+\varepsilon_{\parallel}\mu_{\perp}) + q^2,$

$\tau = \sqrt{\frac{\omega^4}{4}(\varepsilon_{\perp}\mu_{\parallel}-\varepsilon_{\parallel}\mu_{\perp})^2 +\omega^2 q^2(\varepsilon_{\perp}\mu_{\parallel}+\varepsilon_{\parallel}\mu_{\perp} + \varepsilon_{\perp}\mu_{\perp}+\varepsilon_{\parallel}\mu_{\parallel})}.$

Здесь $i$ — мнимая единица.
Каждому собственному значению $\lambda$ соответствует собственный вектор $\vec{\beta}$ : $(m)\vec{\beta}=\lambda\vec{\beta}$ , где

$(m) := \left ( \begin{array}{cccc} 0 & q & 0 & -i\omega\mu_{\perp}\\ -q & 0 & i\omega\mu_{\parallel} & 0\\ 0 & i\omega\varepsilon_{\perp} & 0 & q\\ -i\omega\varepsilon_{\parallel} & 0 & -q & 0 \end{array} \right ).$

Если $\lambda$ кратности 2, то в этой задаче ему соответствует два собственных вектора.
Для каждой $i$ -слоя вычисляется матрица $[D_i]$ . Нумерация слоев слева-направо, по возрастанию координаты $z$ . Формула для вычисления:

$[D_i]=[z_l)(\beta\}\{M_i\}\{\beta)(z_r],$

где

$\{M_i\}= \left ( \begin{array}{cccc} \exp (-\lambda_{1,i} d_i) & 0 & 0 & 0\\ 0 & \exp (-\lambda_{2,i} d_i) & 0 & 0\\ 0 & 0 & \exp (-\lambda_{3,i} d_i) & 0\\ 0 & 0 & 0 & \exp (-\lambda_{4,i} d_i) \end{array} \right ),$

$(\beta\}:= \left ( \begin{array}{llll} \begin{array}{c} {\vdots}\\ \vec{\beta}_1\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_2\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_3\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_4\\ {\vdots} \end{array} \end{array} \right ),$

$[z):= \left ( \begin{array}{cccc} \cos (qz+\varphi_0) & -\sin (qz+\varphi_0) & 0 & 0\\ \sin (qz+\varphi_0) & \cos (qz+\varphi_0) & 0 & 0\\ 0 & 0 & \cos (qz+\varphi_0) & -\sin (qz+\varphi_0)\\ 0 & 0 & \sin (qz+\varphi_0) & \cos (qz+\varphi_0) \end{array} \right ),$

$(z]:= [z)^{-1}$ , $\{\beta):=(\beta\}^{-1}$ , $z_l,z_r$ — координаты соответсвенно левой и правой границы $i$ -слоя: $z_r-z_l=d_i$ .
Формула для вычисления:

$[D] = [D_1]\dots [D_{n-1}][D_n].$

Формула для вычисления:

$\langle U\rangle = \langle 0][D][L\rangle,$

где

$\begin{array}{c} \displaystyle [L\rangle = \left ( \begin{array}{cccc} e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} & 0\\ 0 & e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} \\ 0 & -e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & e^{i\omega\rho_L L}\cdot\rho_L/\mu_L \\ e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & -e^{i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 \end{array} \right ),\\ \displaystyle \langle 0] = \frac{1}{2} \left ( \begin{array}{cccc} 1 & 0 & 0 & \mu_0/\rho_0 \\ 0 & 1 & -\mu_0/\rho_0 & 0\\ 1 & 0 & 0 & -\mu_0/\rho_0 \\ 0 & 1 & \mu_0/\rho_0 & 0 \end{array} \right ), \end{array}$

при $\rho_L = \sqrt{\varepsilon_L\mu_L}$ , $\rho_0 = \sqrt{\varepsilon_0\mu_0}$ .
Предварительные вычисления. Если

$\langle U\rangle = \left ( \begin{array}{cccc} u_{11} & u_{12} & u_{13} & u_{14}\\ u_{21} & u_{22} & u_{23} & u_{24}\\ u_{31} & u_{32} & u_{33} & u_{34}\\ u_{41} & u_{42} & u_{43} & u_{44} \end{array} \right ),$

то вычисляются:

$T:=\left ( \begin{array}{cc} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right )^{-1} = \left ( \begin{array}{cc} t_{11} & t_{12}\\ t_{21} & t_{22} \end{array} \right ),$

$R:= \left ( \begin{array}{cc} u_{31} & u_{32}\\ u_{41} & u_{42} \end{array} \right ) \left ( \begin{array}{cc} t_{11} & t_{12}\\ t_{21} & t_{22} \end{array} \right ) =\left ( \begin{array}{cc} r_{11} & r_{12}\\ r_{21} & r_{22} \end{array} \right ).$

Теперь векторы $\textbf{c}$ записываются:

$\textbf{c}_{x,I} = \left ( \begin{array}{c} 1\\ 0\\ 0\\ 0 \end{array} \right ),\quad \textbf{c}_{x,R} = \left ( \begin{array}{c} 0\\ 0\\ r_{11}\\ r_{21} \end{array} \right ),\quad \textbf{c}_{x,T} = \left ( \begin{array}{c} t_{11}\\ t_{21}\\ 0 \\ 0 \end{array} \right ),$

$\textbf{c}_{y,I}= \left ( \begin{array}{c} 0\\ 1\\ 0\\ 0 \end{array} \right ),\quad \textbf{c}_{y,R}= \left ( \begin{array}{c} 0\\ 0\\ r_{12}\\ r_{22} \end{array} \right ),\quad \textbf{c}_{y,T} = \left ( \begin{array}{c} t_{12}\\ t_{22}\\ 0\\ 0 \end{array} \right ).$

Плоская поляризация Формулы для вычисления:

$\textbf{a}_{x,I}=[0\rangle\textbf{c}_{x,I},\quad \textbf{a}_{x,R}=[0\rangle\textbf{c}_{x,R},\quad \textbf{a}_{x,T}=[L\rangle\textbf{c}_{x,T}.$

$\textbf{a}_{y,I}=[0\rangle\textbf{c}_{y,I},\quad \textbf{a}_{y,R}=[0\rangle\textbf{c}_{y,R},\quad \textbf{a}_{y,T}=[L\rangle\textbf{c}_{y,T}.$

Здесь

$[L\rangle = \left ( \begin{array}{cccc} e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} & 0\\ 0 & e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} \\ 0 & -e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & e^{i\omega\rho_L L}\cdot\rho_L/\mu_L \\ e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & -e^{i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 \end{array} \right ),$

$[0\rangle = \langle 0]^{-1} = \left ( \begin{array}{cccc} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 \\ 0 & -\rho_0/\mu_0 & 0 & \rho_0/\mu_0 \\ \rho_0/\mu_0 & 0 & -\rho_0/\mu_0 & 0 \end{array} \right ),$

при $\rho_L = \sqrt{\varepsilon_L\mu_L}$ , $\rho_0 = \sqrt{\varepsilon_0\mu_0}$ .

Круговая поляризация Формулы для вычисления:

$\textbf{a}_{r,I}=\textbf{a}_{x,I}+i\textbf{a}_{y,I},\quad \textbf{a}_{r,R}=\textbf{a}_{x,R}+i\textbf{a}_{y,R},\quad \textbf{a}_{r,T}=\textbf{a}_{x,T}+i\textbf{a}_{y,T}.$

$\textbf{a}_{l,I}=\textbf{a}_{x,I}-i\textbf{a}_{y,I},\quad \textbf{a}_{l,R}=\textbf{a}_{x,R}-i\textbf{a}_{y,R},\quad \textbf{a}_{l,T}=\textbf{a}_{x,T}-i\textbf{a}_{y,T}.$

Вектор $\textbf{a}$ имеет структуру:

$\textbf{a} := \left ( \begin{array}{c} e_x\\ e_y\\ h_x\\ h_y \end{array} \right ),$

Плотность потока энергии определяется $\langle\textbf{S}\rangle$ — вектором Пойнтинга, усредненным по периоду колебаний:

$\left\langle \textbf{S}(t)\right\rangle = \left\langle\operatorname{Re}[\textbf{E}] \times \operatorname{Re}[\textbf{H}]\right\rangle=\frac{1}{4}\left( \textbf{e} \times \textbf{h}^*+\textbf{e}^* \times \textbf{h} \right),$

где звездочкой ${}^*$ обозначено комплексное сопряжение.

Используя эту формулу вычисляются

$\begin{array}{c} \displaystyle \langle\textbf{S}\rangle_{I,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,I}),\\ \displaystyle \langle\textbf{S}\rangle_{T,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,T}),\\ \displaystyle \langle\textbf{S}\rangle_{R,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,R}), \end{array}$

где $\alpha$ принимает значения $x,y$ (падают волны плоской поляризации) либо $r,l$ (падают волны круговой поляризации).

Для нахождения коэффициента отражения $R$ и коэффициента прохождения $T$ используются формулы:

$T_{\alpha}=\frac{|\langle\textbf{S}\rangle_{T,\alpha}|}{| \langle\textbf{S}\rangle_{I,\alpha}|}, \quad R_{\alpha}=\frac{|\langle\textbf{S}\rangle_{R,\alpha}|}{| \langle\textbf{S}\rangle_{I,\alpha}|}.$

Ну вот. Теперь можно применять. Инструмент забавный. Всем добра.