Вульгаризмы в механике: о вредности термина «замедление»24.04.2017 01:18

Введение
Довольно часто, особенно в обиходе инженерных дисциплин, употребляется понятие «замедление» то есть ускорение, действие которого приводит к уменьшению модуля скорости. При этом такому ускорению приписывается некий отрицательный знак, подчеркивающий этот самый замедляющий эффект.

По моему скромному мнению данное понятие является не только избыточным, но и вредным с методической точки зрения. Оно бросает своего рода мутную вуаль на суть величин, описывающих механическое движение.

На самом деле, чтобы описать то же торможение автомобиля или парашютиста совершенно необязательно приписывать ускорению знак, достаточно понимания, что ускорение есть величина векторная и умения грамотно переходить от операций с векторами к операциям с их проекциями на оси выбранной системы координат.

Статья имеет своей целью развенчать необходимость использования термина «замедление» при решении практических задач механики, и, если читателя не смущает очередная лекция по теормеху, добро пожаловать под кат.

1. Понятие производной от вектора по времени
Рассмотрим вектор $\vec b$ , такой, что

$\vec b = \vec b(t)$

то есть модуль и направление этого вектора зависят от времени. Вычислим изменение изменение этого вектора, произошедшее за промежуток времени $\Delta t$

$(1)$

$\Delta \vec b(t) = \vec b(t + \Delta t) - \vec b(t)$

Теперь, используя тот факт, что для векторов определена операция умножения на число, умножим (1) на величину, обратную приращению времени $\frac{1}{\Delta t}$ . В силу того, что $\Delta t > 0$ мы получим вектор $\frac{1}{\Delta t} \, \Delta \vec b(t)$ , направленный в ту же сторону что и вектор (1) (см. рисунок 1)

Рис. 1. Геометрический смысл производной вектора по времени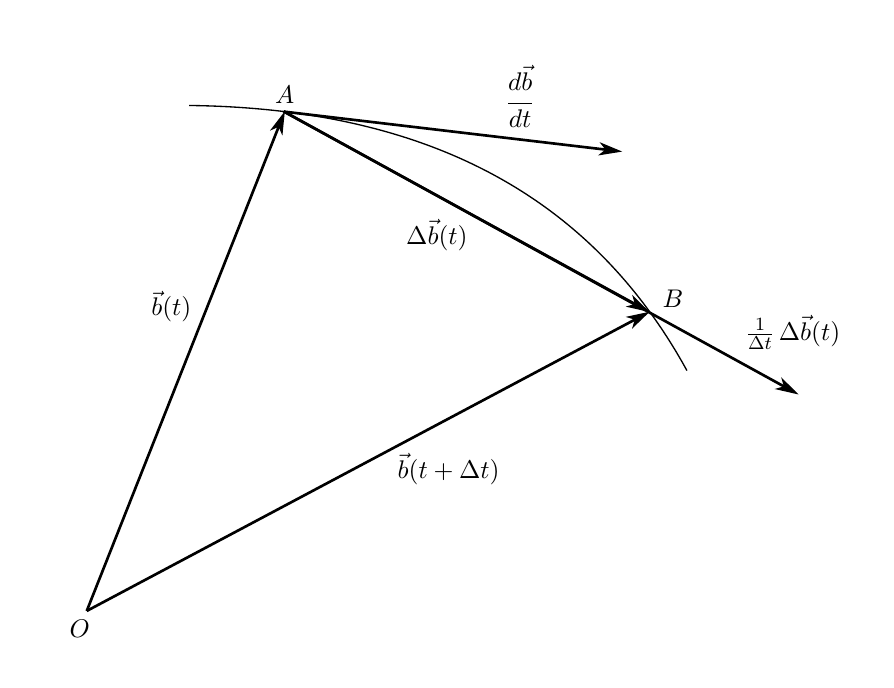

Теперь перейдем к пределу при $\Delta t \to 0$

$(2)$

$\lim_{\Delta t \to 0} \frac{1}{\Delta t} \, \Delta \vec b(t) = \frac{d\vec b}{dt}$

Соотношение (2) есть предел отношения приращения вектор-функции к приращению её аргумента и называется производной вектора по времени. Как видно из наших выкладок производная от вектора по времени также является вектором. Как направлен этот вектор?

Будем рассуждать, глядя на геометрическую интерпретацию на рисунке 1. Вектор $\frac{1}{\Delta t} \, \Delta \vec b(t)$ занимает положение секущей по отношению к траектории, которую описывает конец вектора $\vec b(t)$ за промежуток времени $\Delta t$ . Эта траектория называется годографом вектор-функции $\vec b(t)$ . Секущая пересекает годограф в точках A и B. При стремлении $\Delta t$ к нулю точка A остается неподвижной, а точка B смещается в сторону точки A. В пределе секущая займет положение касательной к годографу в точке A.

То есть, можно ввести следующее определение

Производная от вектора $\vec b(t)$ по времени есть вектор $\frac{d\vec b}{dt}$ , направленный по касательной к годографу вектора $\vec b(t)$

Таким образом, производная от вектора показывает, каким образом меняется как модуль, так и направление вектора. Ни о каком «знаке» производной тут речи не идет в принципе. И не может идти — производная от вектора по времени это так же вектор, а для вектора нет понятия знака.2. Производная от вектора, постоянного по модулю
Допусти теперь что наш вектор обладает неизменной длиной, то есть

$|\vec b(t)| = b = \text{const}$

, а меняется лишь его направление в пространстве. Будет ли у этого вектора отличная от нуля производная? Конечно будет! Умножим вектор скалярно сам на себя

$(3)$

$\vec b \cdot \vec b = |\vec b| \, |\vec b| \, \cos 0 = b^2$

Продифференцируем (3) по времени

$(4)$

$\frac{d}{dt} (\vec b \cdot \vec b) = 2 \, b \, \frac{db}{dt}$

Производная от модуля вектора $\frac{db}{dt}$ равна нулю, ведь модуль не меняется во времени. Тогда, используя правило дифференцирования произведения раскрываем левую часть (4)

$\frac{d\vec b}{dt} \cdot \vec b + \vec b \cdot \frac{d\vec b}{dt} = 0$

используя свойство коммутативности скалярного произведения, получаем

$2 \, \vec b \cdot \frac{d\vec b}{dt} = 0$

или

$\vec b \cdot \frac{d\vec b}{dt} = 0$

То есть, скалярное произведение вектора на собственную производную равно нулю, а значит

$\vec b \perp \frac{d\vec b}{dt}$

Таким образом, производная вектора с постоянной длиной не только не равна нулю, а она есть вектор, перпендикулярный исходному. Годографом такого вектора будет окружность с радиусом, равным длине вектора (рисунок 2).

Мы сталкиваемся с такой ситуацией, когда вычисляем ускорение точки, движущейся равномерно по окружности. У неё есть центростремительное ускорение, перпендикулярное вектору скорости.

Производная от вектора будет равна нулю лишь в том случае, если вектор не меняет ни модуль, ни направление.

Рис 2. Вектор с постоянной длиной, его годограф и производная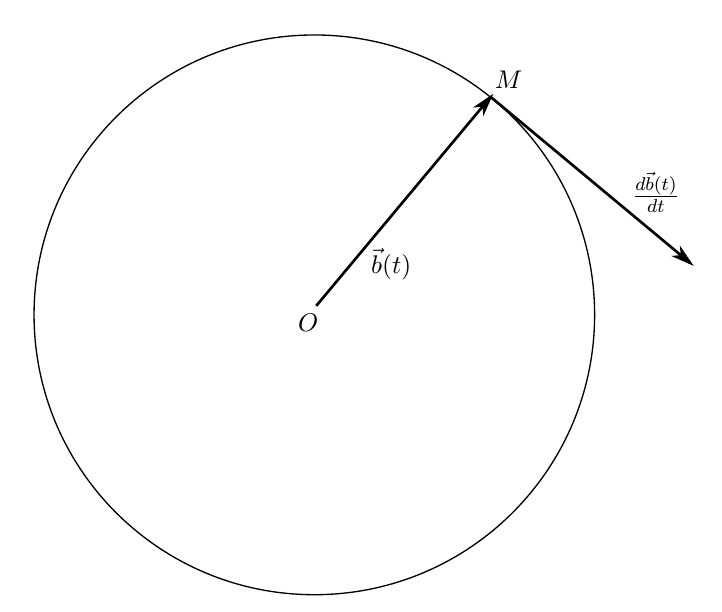

3. Скорость и ускорение
Теперь, исходя из вышеизложенного, дадим определение скорости материальной точки. Пусть положение точки в пространстве характеризуется вектором $\vec r = \vec r(t)$ , называемым радиус-вектором точки (см. рисунок 3). Тогда

Вектором скорости точки $\vec v$ называется первая производная от радиус-вектора точки по времени
$\vec v = \frac{d\vec r}{dt}$

Вектор скорости точки направлен по касательной к её траектории.

Все верно — траектория и есть годограф радиус-вектора, причем выбор начала отсчета O из которого мы выпускаем радиус-вектор роли не играет.

Рис. 3. Векторы скорости и ускорения материальной точки

Аналогичным образом вводится и понятие ускорения

Вектор ускорения точки $\vec a$ есть первая производная от вектора скорости точки по времени
$\vec a = \frac{d\vec v}{dt}$

Вектор ускорения направлен по касательной к годографу вектора скорости.

Геометрическая иллюстрация этих определений показана на рисунке 3. При движении точки по окружности с постоянной по модулю скоростью ускорение направлено точно к центру этой окружности (рисунок 4)

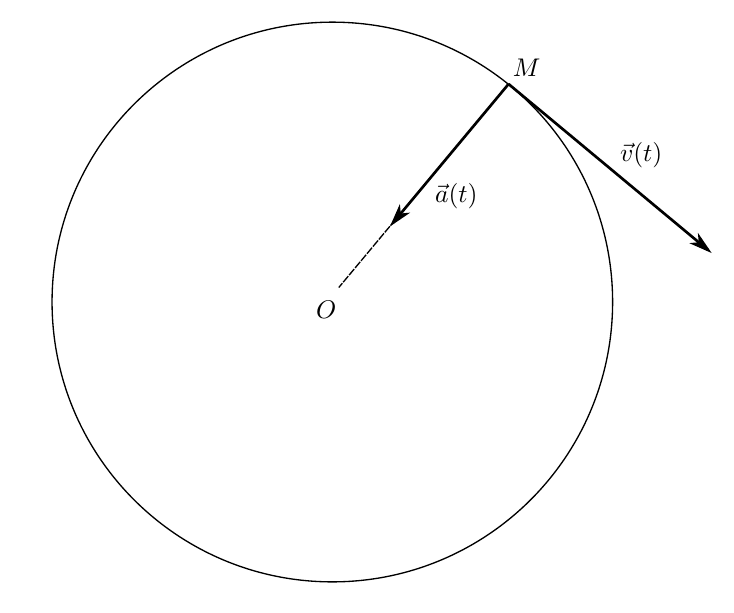
в полном соответствии с определением производной от вектора постоянного по модулю. В этом случае вектор ускорения как раз показывает каким образом меняется направление вектора скорости.

Заключение или откуда всё-таки берется знак
Решая задачу по механике мы неизбежно переходим от векторных уравнений к псевдоскалярным, проецируя векторы на оси выбранной системы координат. И, если вектор ускорения направлен против вектора скорости, то знак его проекции отличается от знака проекции вектора скорости. Причем последняя может быть отрицательной, а проекция ускорения — положительной, все зависит от выбранной системы координат! . Именно в этой ситуации в инженерной практике употребляют термин «замедление».

Однако знак проекции и её именование к механике отношения не имеют, они относятся уже к формальной процедуре вычислений при решении задачи и механического смысла не несут. Так что понятие «замедление» есть результат вольной интерпретации промежуточных результатов вычислений.

Благодарю за проявленное внимание!

Комментарии (16)

NaHCO3

23 апреля 2017 в 18:05

+6

↑

↓

Что-то вы развели панику на пустом месте. Да, ускорение — векторная величина. Что мешает нам ввести классификацию отношений направления вектора ускорения и вектора скорости? Замедление — это когда ускорение направлено в противоположную сторону. Никто же не возражает на классификацию ускорения с делением на тангенциальное и нормальное.
- maisvendoo
  
  23 апреля 2017 в 18:29
  
  0
  
  ↑
  
  ↓
  
  Что мешает нам ввести классификацию отношений направления вектора ускорения и вектора скорости?
  Ничего не мешает нам ввести такую классификацию. Но зачем? Какой смысл во введении избыточных понятий, не несущих физического смысла и являющихся продуктом математических операций, приводящих к решению прикладной задачи.
  И как с такой позиции классифицировать скучай движения точки по окружности с постоянной скоростью? Что это — ускорение или замедление?
  Есть понятие «вектор ускорения», оно предельно просто и включает в себя все прикладные случаи, несет конкретный физический смысл. Зачем плодить лишние сущности?
  - michael_vostrikov
    
    23 апреля 2017 в 20:53
    
    +2
    
    ↑
    
    ↓
    
    Какой смысл во введении избыточных понятий, не несущих физического смысла
    Такой же, как и во введении термина «прямой угол» в отличие от «острого» и «тупого». Есть понятие «угол», оно предельно просто и включает в себя все прикладные случаи. Зачем нам отдельно прямой?
    
    И как с такой позиции классифицировать случай движения точки по окружности с постоянной скоростью? Что это — ускорение или замедление?
    Если это нельзя назвать замедлением, то нельзя назвать и ускорением, так как быстрее она не движется.
    
    Вы не делаете различия между физическим явлением, его частными случаями, и их бытовыми названиями.
    Термин «ускорение» произошел как раз из бытового смысла (а не придуман учеными), как изменение скорости в большую сторону, так как это больше всех интересовало. Обратный случай в быту называют замедлением. В науке оно приобрело более широкий смысл как изменение вектора скорости, не только по значению, но и по направлению. Соответственно, осталось только одно название. Хотя логичнее было бы придумать новый термин.
    
    Для частных случаев часто используются свои названия со своей семантикой, это позволяет более емко и точно передавать информацию. Так что нет никакой проблемы в том, что используется слово «замедление» для описания ситуаций, когда значение скорости уменьшается.
    - maisvendoo
      
      23 апреля 2017 в 21:48 (комментарий был изменён)
      
      0
      
      ↑
      
      ↓
      
      Вы не делаете различия между физическим явлением, его частными случаями, и их бытовыми названиями. Термин «ускорение» произошел как раз из бытового смысла (а не придуман учеными), как изменение скорости в большую сторону, так как это больше всех интересовало.
      «Чойта?» © доктор Быков
      А если мы посмотрим на формулировку второго закона Ньютона, так сказать в оригинале, из «Начал…»
      Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur
      что в переводе с латыни означает: «Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует»
      Отсюда сразу понятно, что Ньютон постулировал связь между изменением количеством движения (суть скоростью при постоянной массе точки) и силой, используя именно векторный характер величин. Причесав всё это своей теорией «флюксий», то есть производных пришел к классической форме уравнений движений точки известной по сей день.
      Так что ввод в науку величин, описывающих механическое движение это сплав эксперимента с хорошей математикой, но никак не плод умозрительного бытового опыта.
      И потом, причем тут быт, когда речь идет о методической постановке вопроса, и правильном понимании смысла вводимых величин, облегчающем оперирование ими
      - maisvendoo
        
        23 апреля 2017 в 22:00
        
        0
        
        ↑
        
        ↓
        
        Оперируя тем же вторым законом и принципом независимости действия сил, можно показать, что ускорение, как продукт действия силы всегда вызывает именно разгон точки в направлении действия силы, поэтому термин «замедление» тут рядом не лежал никак
    - maisvendoo
      
      23 апреля 2017 в 22:05 (комментарий был изменён)
      
      0
      
      ↑
      
      ↓
      
      как изменение скорости в большую сторону
      
      Так что нет никакой проблемы в том, что используется слово «замедление» для описания ситуаций, когда значение скорости уменьшается.
      
      Понятия «больше» и «меньше» к векторным величинам неприменимы. Они применимы к их модулям
- maisvendoo
  
  23 апреля 2017 в 18:32
  
  0
  
  ↑
  
  ↓
  
  Никто же не возражает на классификацию ускорения с делением на тангенциальное и нормальное.
  
  Это не классификация, а форма представления векторного уравнения движения точки в проекциях на естественные оси
- PapaBubaDiop
  
  23 апреля 2017 в 20:11
  
  0
  
  ↑
  
  ↓
  
  А если скорость 0? Вы приплыли…
  - maisvendoo
    
    23 апреля 2017 в 20:14
    
    0
    
    ↑
    
    ↓
    
    Куда я приплыл?
  - maisvendoo
    
    23 апреля 2017 в 20:18
    
    0
    
    ↑
    
    ↓
    
    А если скорость 0?
    
    В какой момент времени? В любой или в какой-то определенный?
    - PapaBubaDiop
      
      23 апреля 2017 в 20:40
      
      0
      
      ↑
      
      ↓
      
      Мяч бросаете. в верхней точке — замедление или ускорение?
      - maisvendoo
        
        23 апреля 2017 в 20:47
        
        0
        
        ↑
        
        ↓
        
        В любой точке траектории мяч движется с ускорением, вектор которого направлен вертикально вниз
        
        PapaBubaDiop
        
        23 апреля 2017 в 21:16
        
        –1
        
        ↑
        
        ↓
        
        Пардон, об этом знает даже мой пятый сын, но мой комментарий был ответом совсем не Вам, а товарищу NaHCO3, чей сомнительный тезис неожиданно заплюсован)
dom1n1k

23 апреля 2017 в 18:27

+3

↑

↓

Не знаю, никогда не встречал на практике, чтобы слово «замедление» использовали как синоним «отрицательному ускорению». Обычно замедление — это бытовое название самого процесса, а не величины, его характеризующей.
- maisvendoo
  
  23 апреля 2017 в 19:06
  
  0
  
  ↑
  
  ↓
  
  Далеко ходить не надо, первая же ссылка по запросу «ускорение и замедление» дает потрясающий опус
  http://av-physics.narod.ru/mechanics/acceleration.htm
  есть и ускорение и замедление и «отрицательное ускорение». Заметьте, не проекция ускорения отрицательна там, а именно ускорение
  Такие подходы популярны в школьных учебниках, например
  - arteast
    
    23 апреля 2017 в 23:15
    
    0
    
    ↑
    
    ↓
    
    Именно так; в учебниках (по крайней мере в том, по которому в свое время учился я) были термины типа «равнозамедленного движения» — с отдельными формулами для них!!! один — и определения типа «если ускорение направлено против направление движения». Потом поверх этого наслаивались задачи в двух измерениях уже в векторах, и картина мира становилась мутной и двоящейся — где там ставить плюсы, где там минусы, и почему?