Второй чемпионат по программированию: разбираем задачи ML-трека
 В октябре состоялся второй чемпионат по программированию. Мы получили 12 500 заявок, более 6000 человек попробовали свои силы в соревнованиях. В этот раз участники могли выбрать один из следующих треков: бэкенд, фронтенд, мобильную разработку и машинное обучение. В каждом треке требовалось пройти квалификационный этап и финал.
В октябре состоялся второй чемпионат по программированию. Мы получили 12 500 заявок, более 6000 человек попробовали свои силы в соревнованиях. В этот раз участники могли выбрать один из следующих треков: бэкенд, фронтенд, мобильную разработку и машинное обучение. В каждом треке требовалось пройти квалификационный этап и финал.
По традиции мы опубликуем разборы треков на Хабре. Начнём с задач квалификационного этапа по машинному обучению. Команда подготовила пять таких задач, из которых составила два варианта по три задачи: в первом варианте были задачи A1, B1 и C, во втором — A2, B2 и C. Варианты случайно распределялись между участниками. Автор задачи C — наш разработчик Павел Пархоменко, остальные задачи составил его коллега Никита Сендерович.
За первую простую алгоритмическую задачу (A1/A2) участники могли получить 50 баллов, правильно реализовав перебор по ответу. За вторую задачу (B1/B2) мы давали от 10 до 100 баллов — в зависимости от эффективности решения. Чтобы получить 100 баллов, требовалось реализовать метод динамического программирования. Третья задача была посвящена построению кликовой модели по предоставленным обучающим данным. В ней требовалось применить методы работы с категориальными признаками и воспользоваться нелинейной моделью обучения (например, градиентным бустингом). За задачу можно было получить до 150 баллов — в зависимости от значения функции потерь на тестовой выборке.
А1. Восстанови длину карусели
Условие
Рекомендательная система должна эффективно определять интересы людей. И помимо методов машинного обучения, для выполнения этой задачи используются специальные интерфейсные решения, которые явным образом спрашивают пользователя, что ему интересно. Одним из таких решений является карусель.
Карусель — это горизонтальная лента из карточек, каждая из которых предлагает подписаться на конкретный источник или тему. Одна и та же карточка может встречаться в карусели несколько раз. Карусель можно прокручивать слева направо, при этом после последней карточки пользователь снова видит первую. Для пользователя переход от последней карточки к первой незаметен, с его точки зрения лента бесконечна.
В какой-то момент любопытный пользователь Василий заметил, что лента на самом деле зациклена, и решил выяснить истинную длину карусели. Для этого он стал прокручивать ленту и последовательно выписывать встречающиеся карточки, для простоты обозначая каждую карточку строчной латинской буквой. Так Василий выписал первые n карточек на листок бумаги. Гарантируется, что он просмотрел все карточки карусели хотя бы один раз. Потом Василий лёг спать, а утром обнаружил, что кто-то пролил стакан с водой на его записи и некоторые буквы теперь невозможно распознать.
По оставшейся информации помогите Василию определить наименьшее возможное количество карточек в карусели.
Формат ввода
В первой строке задано одно целое число n (1 ≤ n ≤ 1000) — количество символов, выписанных Василием.
Вторая строка содержит выписанную Василием последовательность. Она состоит из n символов — строчных букв латинского алфавита и знака #, который обозначает, что букву на этой позиции невозможно распознать.
Формат вывода
Выведите одно целое положительное число — наименьшее возможное количество карточек в карусели.
Пример 1
Пример 2
Пример 3
Пример 4
Примечания
В первом примере все буквы удалось распознать, минимальная карусель могла состоять из 3 карточек — abc.
Во втором примере все буквы удалось распознать, минимальная карусель могла состоять из 3 карточек — abb. Обратите внимание, что вторая и третья карточки в этой карусели одинаковые.
В третьем примере наименьшая возможная длина карусели получается, если предположить, что на третьей позиции находился символ a. Тогда исходная строка — ababa, минимальная карусель состоит из 2 карточек — ab.
В четвёртом примере исходная строка могла быть любой, например ffffff. Тогда карусель могла состоять из одной карточки — f.
Система оценки
Только при прохождении всех тестов за задачу можно получить 50 баллов.
В тестирующей системе тесты 1–4 — примеры из условия.
Решение
Достаточно было перебрать возможную длину карусели от 1 до n и для каждой фиксированной длины проверить, могла ли она быть таковой. При этом понятно, что ответ всегда существует, поскольку значение n гарантированно является возможным ответом. Для фиксированной длины карусели p достаточно проверить, что в переданной строке для всех i от 0 до (p — 1) на всех позициях i, i + p, i + 2p и т. д. находятся одинаковые символы или #. Если хотя бы для какого-то i встречается 2 различных символа из диапазона от a до z, то карусель не может быть длины p. Поскольку в худшем случае для каждого p нужно пробежаться по всем символам строки один раз, сложность такого алгоритма — O (n2).
def check_character(char, curchar):
return curchar is None or char == "#" or curchar == char
def need_to_assign_curchar(char, curchar):
return curchar is None and char != "#"
n = int(input())
s = input().strip()
for p in range(1, n + 1):
is_ok = True
for i in range(0, p):
curchar = None
for j in range(i, n, p):
if not check_character(s[j], curchar):
is_ok = False
break
if need_to_assign_curchar(s[j], curchar):
curchar = s[j]
if not is_ok:
break
if is_ok:
print(p)
breakА2. Восстанови длину карусели
Условие
Рекомендательная система должна эффективно определять интересы людей. И помимо методов машинного обучения, для выполнения этой задачи используются специальные интерфейсные решения, которые явным образом спрашивают пользователя, что ему интересно. Одним из таких решений является карусель.
Карусель — это горизонтальная лента из карточек, каждая из которых предлагает подписаться на конкретный источник или тему. Одна и та же карточка может встречаться в карусели несколько раз. Карусель можно прокручивать слева направо, при этом после последней карточки пользователь снова видит первую. Для пользователя переход от последней карточки к первой незаметен, с его точки зрения лента бесконечна.
В какой-то момент любопытный пользователь Василий заметил, что лента на самом деле зациклена, и решил выяснить истинную длину карусели. Для этого он стал прокручивать ленту и последовательно выписывать встречающиеся карточки, для простоты обозначая каждую карточку строчной латинской буквой. Так Василий выписал первые n карточек. Гарантируется, что он просмотрел все карточки карусели хотя бы один раз. Поскольку Василий отвлекался на содержимое карточек, при выписывании он мог по ошибке заменять одну букву на другую, но известно, что всего он сделал не более k ошибок.
Вам в руки попали записи, сделанные Василием, вы также знаете значение k. Определите, какое наименьшее количество карточек могло быть в его карусели.
Формат ввода
В первой строке заданы два целых числа: n (1 ≤ n ≤ 500) — количество символов, выписанных Василием, и k (0 ≤ k ≤ n) — максимальное число ошибок, которое допустил Василий.
Вторая строка содержит n строчных букв латинского алфавита — выписанная Василием последовательность.
Формат вывода
Выведите одно целое положительное число — наименьшее возможное количество карточек в карусели.
Пример 1
Пример 2
Пример 3
Пример 4
Примечания
В первом примере k = 0, и мы точно знаем, что Василий не ошибался, минимальная карусель могла состоять из 3 карточек — abc.
Во втором примере наименьшая возможная длина карусели получается, если предположить, что Василий по ошибке заменил третью букву a на c. Тогда настоящая строка — ababa, минимальная карусель состоит из 2 карточек — ab.
В третьем примере известно, что Василий мог сделать одну ошибку. Однако размер карусели минимален, если предположить, что он не делал ошибок. Минимальная карусель состоит из 3 карточек — abb. Обратите внимание, что вторая и третья карточки в этой карусели одинаковые.
В четвёртом примере мы можем сказать, что Василий ошибся при вводе всех букв, и исходная строка на самом деле могла быть любой, например ffffff. Тогда карусель могла состоять из одной карточки — f.
Система оценки
Только при прохождении всех тестов за задачу можно получить 50 баллов.
В тестирующей системе тесты 1–4 — примеры из условия.
Решение
Достаточно было перебрать возможную длину карусели от 1 до n и для каждой фиксированной длины проверить, могла ли она быть таковой. При этом понятно, что ответ всегда существует, поскольку значение n гарантированно является возможным ответом, каким бы ни было значение k. Для фиксированной длины карусели p достаточно посчитать независимо для всех i от 0 до (p — 1), какое минимальное количество ошибок допущено на позициях i, i + p, i + 2p и т. д. Это число ошибок минимально, если принять за истинный символ тот, который встречается на этих позициях чаще всех. Тогда число ошибок равно количеству позиций, на которых стоит другая буква. Если для некоторого p общее число ошибок не превосходит k, то значение p является возможным ответом. Поскольку для каждого p нужно пробежаться по всем символам строки один раз, сложность такого алгоритма — O (n2).
n, k = map(int, input().split())
s = input().strip()
for p in range(1, n + 1):
mistakes = 0
for i in range(0, p):
counts = [0] * 26
for j in range(i, n, p):
counts[ord(s[j]) - ord("a")] += 1
mistakes += sum(counts) - max(counts)
if mistakes <= k:
print(p)
breakB1. Оптимальная лента рекомендаций
Условие
Формирование очередной порции персональной выдачи рекомендаций для пользователя — непростая задача. Рассмотрим n публикаций, выбранных из рекомендательной базы по итогам отбора кандидатов. Публикация под номером i характеризуется оценкой релевантности si и набором из k бинарных атрибутов ai1, ai2, …, aik. Каждый из этих атрибутов отвечает некоторому свойству публикации, к примеру, подписан ли пользователь на источник этой публикации, была ли публикация создана за последние 24 часа и т. д. Публикация может обладать сразу несколькими из этих свойств одновременно — в таком случае соответствующие атрибуты принимают значение 1, а может и не обладать ни одним из них — и тогда все её атрибуты равны 0.
Для того чтобы лента пользователя была разнообразной, необходимо выбрать среди n кандидатов m публикаций так, чтобы среди них оказалось не менее A1 публикаций, обладающих первым свойством, не менее A2 публикаций, обладающих вторым свойством, …, Ak публикаций, обладающих свойством под номером k. Найдите максимально возможную суммарную оценку релевантности m публикаций, удовлетворяющих этому требованию, либо определите, что такого набора публикаций не существует.
Формат ввода
В первой строке заданы три целых числа — n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
В следующих n строках заданы характеристики публикаций. Для i-й публикации задано целое число si (1 ≤ si ≤ 109) — оценка релевантности данной публикации, и далее через пробел строка из k символов, каждый из которых равен 0 или 1 — значения каждого из атрибутов данной публикации.
В последней строке заданы k целых чисел, разделённых пробелами — значения A1, …, Ak (0 ≤ Ai ≤ m), определяющие требования к итоговому набору из m публикаций.
Формат вывода
Если не существует набора из m публикаций, удовлетворяющих ограничениям, выведите число 0. Иначе выведите одно целое положительное число — максимально возможную суммарную оценку релевантности.
Пример 1
Пример 2
Примечания
В первом примере необходимо из четырёх публикаций с двумя свойствами выбрать две так, чтобы было не менее одной публикации, обладающей первым свойством, и одной, обладающей вторым свойством. Самую большую сумму релевантностей можно получить, если взять вторую и третью публикации, хотя под ограничения также подходит любой вариант с четвёртой публикацией.
Во втором примере невозможно выбрать две публикации так, чтобы обе обладали вторым свойством, ибо им обладает только первая публикация.
Система оценки
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Прохождение тестов из условия необходимо для получения баллов за группы начиная со второй. Всего за задачу можно получить 100 баллов.
В тестирующей системе тесты 1–2 — примеры из условия.
1. (10 баллов) тесты 3–10: k = 1, m ≤ 3, si ≤ 1000, не требуется прохождение тестов из условия
2. (20 баллов) тесты 11–20: k ≤ 2, m ≤ 3
3. (20 баллов) тесты 21–29: k ≤ 2
4. (20 баллов) тесты 30–37: k ≤ 3
5. (30 баллов) тесты 38–47: нет дополнительных ограничений
Решение
Есть n публикаций, у каждой есть скор и k булевых флажков, требуется выбрать m карточек, таких что сумма релевантностей максимальна и выполнено k требований вида «среди выбранных m публикаций должно быть ≥ Ai карточек с i-ым флажком», либо определить, что такого набора публикаций не существует.
Решение на 10 баллов: если есть ровно один флажок, достаточно взять A1 публикаций с этим флажком, имеющих наибольшую релевантность (если таких карточек меньше, чем A1, то искомого набора не существует), а остальные (m — A1) добрать оставшимися карточками с наилучшей релевантностью.
Решение на 30 баллов: если m не превосходит 3, то можно найти ответ полным перебором всевозможных O (n3) троек карточек, выбрать наилучший по суммарной релевантности вариант, удовлетворяющий ограничениям.
Решение на 70 баллов (на 50 баллов всё то же самое, только проще реализовать): если есть не более 3 флажков, то можно разбить все публикации на 8 непересекающихся групп по набору флажков, которыми они обладают: 000, 001, 010, 011, 100, 101, 110, 111. Публикации в каждой группе нужно отсортировать по убыванию релевантности. Далее можно за O (m4) перебрать, сколько лучших публикаций мы берём из групп 111, 011, 110 и 101. Из каждой берём от 0 до m публикаций, в сумме не более m. После этого становится ясно, сколько публикаций необходимо добрать из групп 100, 010 и 001, чтобы требования удовлетворялись. Остаётся добрать до m оставшимися карточками с наилучшей релевантностью.
Полное решение: рассмотрим функцию динамического программирования dp[i][a]…[z]. Это максимальная суммарная оценка релевантности, которую можно получить, использовав ровно i публикаций, чтобы было ровно a публикаций с флажком A, …, z публикаций с флажком Z. Тогда исходно dp[0][0]…[0] = 0, а для всех остальных наборов параметров значение положим равным -1, чтобы в дальнейшем максимизировать это значение. Далее будем «вводить в игру» карточки по одной и с помощью каждой карточки улучшать значения этой функции: для каждого состояния динамики (i, a, b, …, z) с помощью j-й публикации с флажками (aj, bj, …, zj) можно попробовать совершить переход в состояние (i + 1, a + aj, b + bj, …, z + zj) и проверить, не улучшится ли результат в этом состоянии. Важно: при переходе нас не интересуют состояния, где i ≥ m, поэтому всего состояний у такой динамики не более mk + 1, и итоговая асимптотика — O (nmk + 1). Когда посчитаны состояния динамики, ответом является состояние, которое удовлетворяет ограничениям и даёт наибольшую суммарную оценку релевантности.
С точки зрения реализации для ускорения работы программы полезно хранить состояние динамического программирования и флажки каждой из публикаций в упакованном виде в одном целом числе (см. код), а не в списке или кортеже. Такое решение использует меньше памяти и позволяет эффективно производить апдейты состояний динамики.
Код полного решения:
def pack_state(num_items, counts):
result = 0
for count in counts:
result = (result << 8) + count
return (result << 8) + num_items
def get_num_items(state):
return state & 255
def get_flags_counts(state, num_flags):
flags_counts = [0] * num_flags
state >>= 8
for i in range(num_flags):
flags_counts[num_flags - i - 1] = state & 255
state >>= 8
return flags_counts
n, m, k = map(int, input().split())
scores, attributes = [], []
for i in range(n):
score, flags = input().split()
scores.append(int(score))
attributes.append(list(map(int, flags)))
limits = list(map(int, input().split()))
dp = {0 : 0}
for i in range(n):
score = scores[i]
state_delta = pack_state(1, attributes[i])
dp_temp = {}
for state, value in dp.items():
if get_num_items(state) >= m:
continue
new_state = state + state_delta
if value + score > dp.get(new_state, -1):
dp_temp[new_state] = value + score
dp.update(dp_temp)
best_score = 0
for state, value in dp.items():
if get_num_items(state) != m:
continue
flags_counts = get_flags_counts(state, k)
satisfied_bounds = True
for i in range(k):
if flags_counts[i] < limits[i]:
satisfied_bounds = False
break
if not satisfied_bounds:
continue
if value > best_score:
best_score = value
print(best_score)B2. Приближение функции
Условие
Для оценки степени релевантности документов используются различные методы машинного обучения — например, решающие деревья. k-ичное решающее дерево имеет в каждом узле решающее правило, которое разделяет объекты на k классов по значениям некоторого признака. На практике обычно используются двоичные решающие деревья. Рассмотрим упрощённую версию задачи оптимизации, которую необходимо решать в каждом узле k-ичного решающего дерева.
Пусть дискретная функция f определена в точках i = 1, 2, …, n. Необходимо найти кусочно-постоянную функцию g, состоящую не более чем из k участков постоянства, такую что значение SSE = (g (i) — f (i))2 минимально.
Формат ввода
В первой строке заданы два целых числа n и k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
Во второй строке задано n целых чисел f (1), f (2), …, f (n) — значения приближаемой функции в точках 1, 2, …, n (–106 ≤ f (i) ≤ 106).
Формат вывода
Выведите единственное число — минимальное возможное значение SSE. Ответ считается правильным, если абсолютная или относительная погрешность не превосходит 10–6.
Пример 1
Пример 2
Пример 3
Примечания
В первом примере оптимальная функция g — константа g (i) = 2.
SSE = (2 — 1)2 + (2 — 2)2 + (2 — 3)2 = 2.
Во втором примере есть 2 варианта. Либо g (1) = 1 и g (2) = g (3) = 2.5, либо g (1) = g (2) = 1.5 и
g (3) = 3. В любом случае SSE = 0.5.
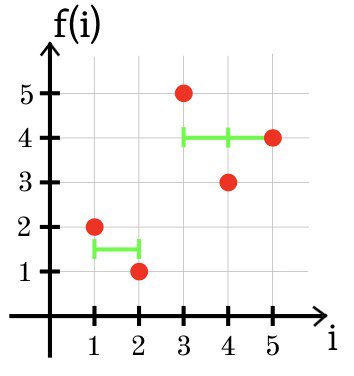
В третьем примере оптимальное приближение функции f с помощью двух участков постоянства изображено ниже: g (1) = g (2) = 1.5 и g (3) = g (4) = g (5) = 4.
SSE = (1.5 + 2)2 + (1.5 — 1)2 + (4 — 5)2 + (4 — 3)2 + (4 — 4)2 = 2.5.
Система оценки
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Прохождение тестов из условия необходимо для получения баллов за группы начиная со второй. Всего за задачу можно получить 100 баллов.
В тестирующей системе тесты 1–3 — примеры из условия.
1. (10 баллов) тесты 4–22: k = 1, не требуется прохождение тестов из условия
2. (20 баллов) тесты 23–28: k ≤ 2
3. (20 баллов) тесты 29–34: k ≤ 3
4. (20 баллов) тесты 35–40: k ≤ 4
5. (30 баллов) тесты 41–46: нет дополнительных ограничений
Решение
Как известно, константа, которая минимизирует значение SSE для набора значений f1, f2, …, fn, — это среднее перечисленных здесь значений. При этом, как нетрудно убедиться путём простых выкладок, само значение SSE = .
Решение на 10 баллов: просто считаем среднее всех значений функции и SSE за O (n).
Решение на 30 баллов: перебираем последнюю точку, относящуюся к первому участку постоянства из двух, для фиксированного разбиения вычисляем SSE и выбираем оптимальное. Кроме того, важно не забыть разобрать кейс, когда участок постоянства только один. Сложность — O (n2).
Решение на 50 баллов: перебираем границы разбиения на участки постоянства за O (n2), для фиксированного разбиения на 3 отрезка вычисляем SSE и выбираем оптимальное. Сложность — O (n3).
Решение на 70 баллов: предподсчитываем суммы и суммы квадратов значений fi на префиксах, это позволит быстро считать среднее и SSE на любом отрезке. Перебираем границы разбиения на 4 участка постоянства за O (n3), с помощью предподсчитанных значений на префиксах за O (1) вычисляем SSE. Сложность — O (n3).
Полное решение: рассмотрим функцию динамического программирования dp[s][i]. Это наименьшее значение SSE, если приближать первые i значений с помощью s отрезков. Тогда
dp[0][0] = 0, а для всех остальных наборов параметров значение положим равным бесконечности, чтобы в дальнейшем минимизировать это значение. Будем решать задачу, постепенно увеличивая значение s. Как вычислить dp[s][i], если уже посчитаны значения динамики для всех меньших s? Достаточно обозначить за t количество первых точек, покрытых предыдущими (s — 1) отрезками, и перебрать все значения t, а остальные (i — t) точек приблизить с помощью оставшегося отрезка. Нужно выбрать наилучшее по итоговому SSE на i точках значение t. Если предподсчитать суммы и суммы квадратов значений fi на префиксах, то это приближение будет производиться за O (1), и значение dp[s][i] удастся вычислить за O (n). Итоговым ответом будет значение dp[k][n]. Итоговая сложность алгоритма — O (kn2).
Код полного решения:
n, k = map(int, input().split())
f = list(map(float, input().split()))
prefix_sum = [0.0] * (n + 1)
prefix_sum_sqr = [0.0] * (n + 1)
for i in range(1, n + 1):
prefix_sum[i] = prefix_sum[i - 1] + f[i - 1]
prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2
def get_best_sse(l, r):
num = r - l + 1
s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2
ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1]
return ss - s_sqr / num
dp_curr = [1e100] * (n + 1)
dp_prev = [1e100] * (n + 1)
dp_prev[0] = 0.0
for num_segments in range(1, k + 1):
dp_curr[num_segments] = 0.0
for num_covered in range(num_segments + 1, n + 1):
dp_curr[num_covered] = 1e100
for num_covered_previously in range(num_segments - 1, num_covered):
dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered))
dp_curr, dp_prev = dp_prev, dp_curr
print(dp_prev[n])C. Предсказание кликов пользователя
Условие
Одним из важнейших сигналов для рекомендательной системы является поведение пользователя. Таких данных зачастую достаточно, чтобы построить бейзлайн приемлемого качества.
В этом задании вам нужно построить рекомендательную систему на основе данных о действиях пользователей в персональной ленте рекомендаций Яндекс.Дзена.
Вам доступны 2 датасета: тренировочный (train.csv) и тестовый (test.csv). Каждая строка в датасетах соответствует взаимодействию некоторого пользователя с некоторым документом, показанным ему в ленте рекомендаций. Датасеты содержат следующие колонки:
— sample_id — числовой id взаимодействия,
— item — числовой id показанного пользователю документа,
— publisher — числовой id автора документа,
— user — числовой id пользователя,
topic_i, weight_i — числовой id i-ой темы документа и степень принадлежности документа данной теме (целое число от 0 до 100) (i = 0, 1, 2, 3, 4),
— target — факт клика пользователя на документ (1 — был клик, 0 — был показ без клика). Этот столбец присутствует только в тренировочном датасете.
Необходимо построить модель для предсказания кликов пользователя и применить её к тестовому датасету.
Гарантируется, что все встречающиеся в тестовом датасете значения столбцов item, publisher, user, topic встречаются и в тренировочном датасете.
В качестве решения нужно отправить csv-файл, состоящий из двух колонок: sample_id и target, где sample_id — id строки из тестового датасета, а target — предсказанная вероятность клика. Количество строк в этом файле должно совпадать с количеством строк в test.csv. Строки в файле с решением должны быть отсортированы по возрастанию значений колонки sample_id (в том же порядке, что и в test.csv). Все значения вероятностей в колонке target должны быть вещественными числами от 0 до 1.
Для оценки качества отправленного решения используется метрика logloss.
За эту задачу можно получить максимум 150 баллов. Для конвертации метрики logloss в баллы используется следующая функция:
$$display$$\begin{equation*} score = \begin{cases} 0 &\text{, logloss > 0.5}\\ min (150,(200 * (0.5 — logloss))^2) &\text{, logloss ≤ 0.5} \end{cases} \end{equation*}$$display$$
При отправке решения logloss вычисляется сразу на всём тестовом датасете и конвертируется в итоговый балл за посылку. Баллы считаются с точностью до 2 знаков после запятой, logloss решения показывается с точностью до 4 знаков после запятой.
Формат ввода
Фрагмент train.csv:
Фрагмент test.csv:
Формат вывода
Фрагмент возможного файла с решением:
Примечания
Датасеты можно скачать по ссылке: yadi.sk/d/pVna8ejcnQZK_A. Там же вы сможете найти бейзлайн, который поможет приступить к задаче.
Для подсчета значения метрики logloss на одном объекте тестового датасета используется следующая функция:
EPS = 1e-4
def logloss (y_true, y_pred):
if abs(y_pred — 1) < EPS:
y_pred = 1 — EPS
if abs(y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log (y_pred) — (1 — y_true) ∗ log (1 — y_pred)
Итоговый logloss за посылку вычисляется как среднее значение logloss по всем объектам тестового датасета.
Для подсчета баллов по logloss используется следующая функция:
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2)
Решение
Нужно предсказать, понравится ли пользователю публикация. Есть разные способы решить задачу. Надо учитывать, что все сущности (документы, пользователи, источники, темы) одинаковые как в тренировочном, так и в тестовом датасете — то есть нет проблем с тем, что о каких-то документах из тестового датасета мы не знаем, как с ними взаимодействуют пользователи.
Мы опишем некоторые подходы участников, набравших 100 и более баллов (из 150).
Самый простой способ — загрузить датасет в CatBoost и аккуратно подобрать гиперпараметры. Поскольку CatBoost умеет хорошо обрабатывать категориальные признаки (которых было большинство в исходном датасете), даже такое простое решение давало хороший результат. Чтобы повысить качество работы метода, можно было сгенерировать больше признаков. К примеру, сделать разные признаки-счётчики: кликабельность документа , пользователя, источника, тем, какие-то парные взаимодействия (как часто пользователь кликает на темы статьи).
Хороший результат можно было получить и с помощью коллаборативных методов. Например, можно было использовать разложение матрицы документ-пользователь или методы, которые учитывают другие доступные данные: FM (Factorization Machines) и FFM (Field-aware Factorization Machines).
Если вы планируете участвовать в соревнованиях по машинному обучению, посмотрите разбор ML-трека первого чемпионата.
