Временные ряды. Простые решения22.04.2021 05:32

Привет, Хабр!

В этой статье мы рассмотрим несколько простых подходов прогнозирования временных рядов.

Материал, изложенный в статье, на мой взгляд, хорошо дополняет первую неделю курса «Прикладные задачи анализа данных» от МФТИ и Яндекс. На обозначенном курсе можно получить теоретические знания, достаточные для решения задач прогнозирования рядов динамики, а в качестве практического закрепления материала предлагается с помощью модели ARIMA библиотеки scipy сформировать прогноз заработной платы в Российской Федерации на год вперед. В статье, мы также будем формировать прогноз заработной платы, но при этом будем использовать не библиотеку scipy, а библиотеку sklearn. Фишка в том, что в scipy уже предусмотрена модель ARIMA, а sklearn не располагает готовой моделью, поэтому нам придется потрудиться ручками. Таким образом, нам для решения задачи, в каком то смысле, необходимо будет разобраться как устроена модель изнутри. Также, в качестве дополнительного материала, в статье, задача прогнозирования решается с помощью однослойной нейронной сети библиотеки pytorch.
Весь код написан на python 3 в jupyter notebook. Более того, notebook устроен таким образом, что вместо данных о заработной плате можно подставить многие другие ряды динамики, например данные о ценах на сахар, поменять период прогнозирования, валидации и обучения, добавить иные внешние факторы и сформировать соответствующий прогноз. Другими словами, в работе используется простенький самописный тренажерчик, с помощью которого можно прогнозировать различные ряды динамики. Код можно посмотреть здесь

План статьи

Краткое описание тренажера.
Решение в лоб — прогнозирование временных рядов с использованием только «сырых» данных прошлых значений рядов динамики.
Добавление экзогенных переменных.
Коррекция гетероскедастичности через логарифмирование исходных данных.
Приведение ряда к стационарному.
Прогнозирование с помощью однослойной нейронной сети.
Сравнение подходов.
Полезные ссылки

Краткое описание тренажера

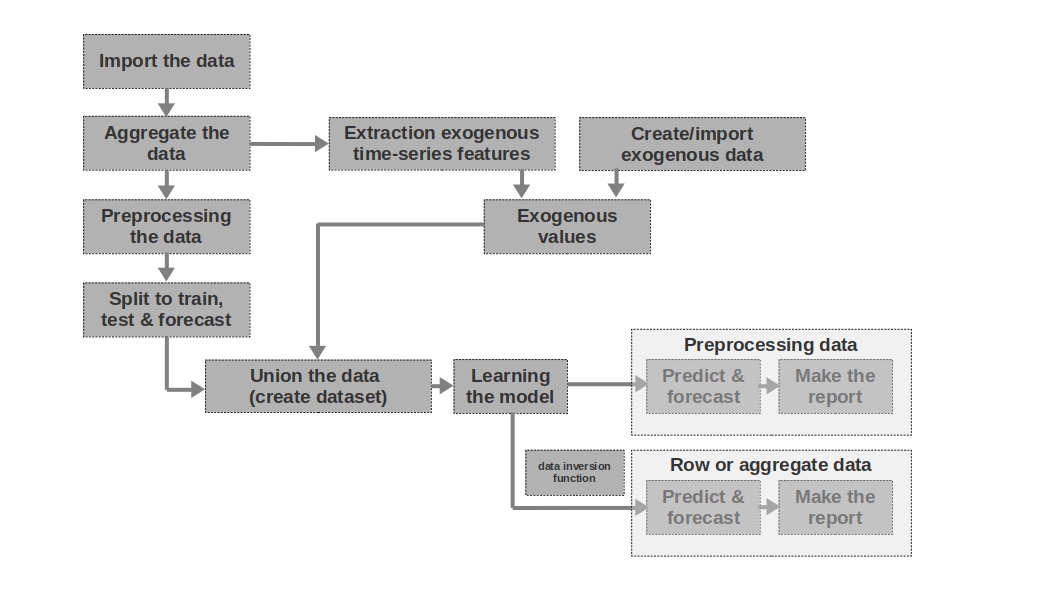
Import the data
Здесь все просто — импортируем данные. Иногда бывает так, что сырых данных достаточно для формирования более-менее внятного прогноза. Именно первый и второй прогнозы в статье моделируются на основании сырых данных, то есть для прогноза заработной платы используются необработанные данные о заработной плате в прошлые периоды.

Aggregate the data
В статье не используется агрегация данных ввиду отсутствия необходимости. Однако зачастую, данные могут быть представлены неравными временными интервалами. В таком случае, просто необходимо их агрегировать. Например, данные с торгов ценными бумагами, валютой и другими финансовыми инструментами необходимо агрегировать. Обычно берут среднее значение в интервале, но можно и максимальное, минимальное, стандартное отклонение и другие статистики.

Preprocessing the data
В нашем случае, речь идет в первую очередь о предобработке данных, благодаря которой, временной ряд приобретает свойство гомоскедастичности (через логарифмирование данных) и становится стационарным (через дифференцирование ряда).

Split to train, test & forecast
В этом блоке кода временные ряды разбиваются на периоды обучения, тестирования и прогнозирования путем добавления нового столбца с соответствующими значениями «train», «test», «forecast». То есть, мы не создаем три отдельных таблицы для каждого периода, а просто добавляем столбец, на основании, которого в дальнейшем будем разделять данные.

Extraction exogenous time-series features
Бывает полезным выделить дополнительные внешние (экзогенные) признаки из временного ряда. Например, указать выходной это день или нет, указать количество дней в месяце (или количество рабочих дней в месяце) и др. Как правило эти признаки «вытаскиваются» из самого временного ряда без какого либо ручного вмешательства.

Create/import exogenous data
Не всю информацию можно «вытащить» из временного ряда. Иногда могут потребоваться дополнительные внешние данные. Например, какие-то эпизодические события, которые оказывают сильное влияние на значения временного ряда. Такими событиями могут быть даты начала военных действий, введения санкций, природные катаклизмы и др. В работе такие факторы не рассматриваются, однако возможность их использования стоит иметь в виду.

Exogenous values
В этом блоке кода мы объединяем все экзогенные данные в одну таблицу.

Union the data (create dataset)
В этом блоке кода мы объединяем значения временного ряда и экзогенных признаков в одну таблицу. Другими словами — готовим датасет, на основании, которого будем обучать модель, тестировать качество и формировать прогноз.

Learning the model
Здесь все понятно — мы просто обучаем модель.

Preprocessing data: predict & forecast
В случае, если мы для обучения модели использовали предобаботанные данные (логарифмированные, обработанные функцией бокса-кокса, стационарный ряд и др.), то качество модели для начала оценивается на предобработанных данных и только потом уже на «сырых» данных. Если, мы данные не предобрабатывали, то данный этап пропускается.

Row data: predict & forecast
Данный этап является заключительным. Если, модель обучалась на предобработанных данных, например, мы их прологарифмировали, то для получения прогноза заработной платы в рублях, а не логарифма рублей, нам следует перевести прогноз обратно в рубли.

Также хотелось бы отметить, что в статье используется одномерный временной ряд для предсказания заработной платы. Однако ничего не мешает использовать многомерный ряд, например добавить данные курса рубля к доллару или какой-либо другой ряд.

Решение в лоб

Будем считать, что данные о заработной плате в прошлом, могут аппроксимировать заработную плату в будущем. Иначе можно сказать — размер заработной платы, например, в январе зависит от того, какая заработная плата была в декабре, ноябре, октябре, …

Давайте возьмем значения заработной платы в 12-ть прошлых месяцев для предсказания заработной платы в 13-й месяц. Другими словами для каждого целевого значения у нас будет 12 признаков.

Признаки будем подавать на вход Ridge Regression библиотеки sklearn. Параметры модели берем по умолчанию за исключением параметра alpha, его установили на 0, то есть по сути мы используем обычную регрессию.

Это и есть решение в лоб — оно самое простое:) Бывают ситуации, когда нужно очень срочно дать хоть какой-то результат, а времени на какую-либо предобработку просто нет или не хватает опыта, чтобы оперативно обработать или добавить данные. Вот в таких ситуациях, можно в качестве baseline использовать сырые данные для построения прогноза. Забегая вперед, отмечу, что качество модели оказалось сопоставимо с качеством моделей, в которых используется предобработка данных.

Давайте посмотрим, что у нас получилось.

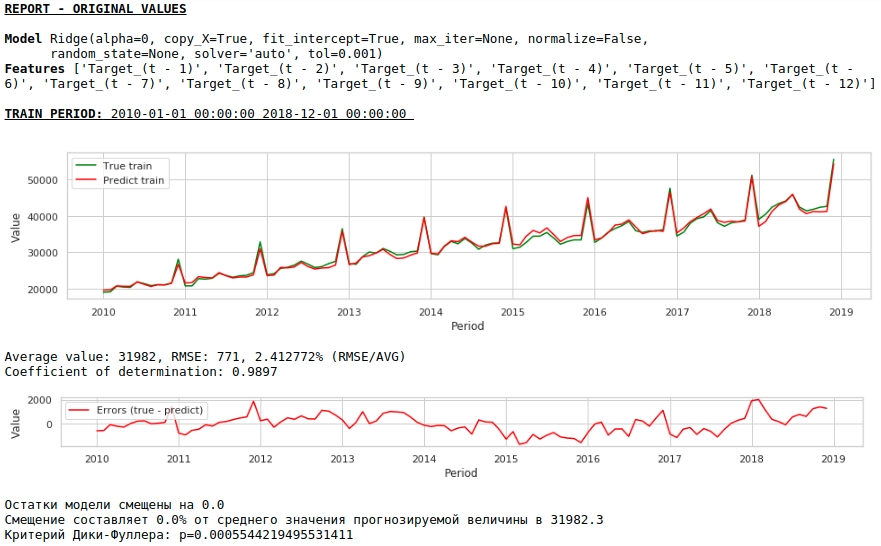
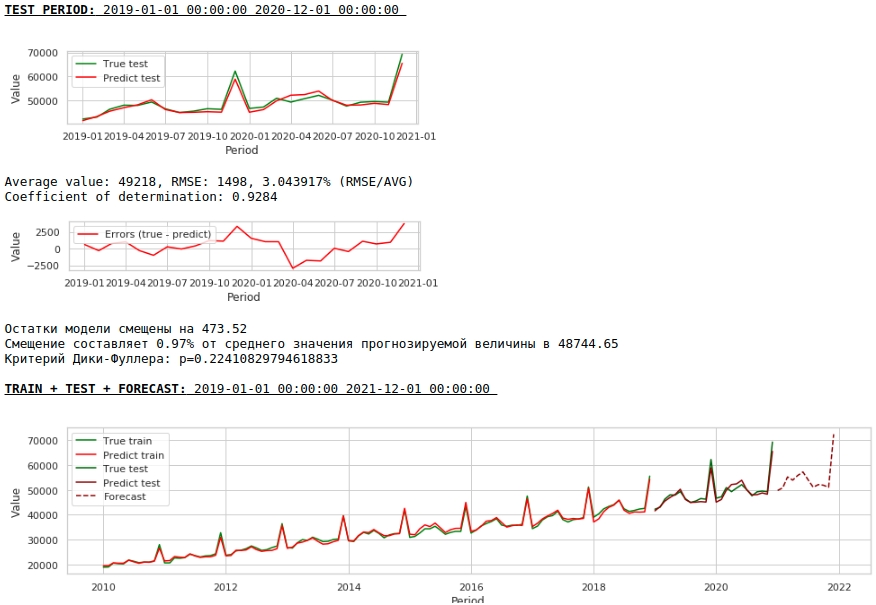
На первый взгляд результат выглядит хоть и неидеально, но близко к действительности.

В соответствии со значениями коэффициентов регрессии, наибольшее влияние на прогноз заработной платы оказывает значение заработной платы ровно год назад.

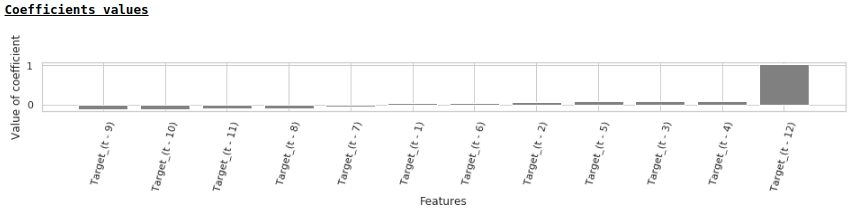
Попробуем добавить в модель экзогенные переменные.

Добавление экзогенных переменных

Мы будем использовать 2 внешних признака: количество дней в месяце и номер месяца (от 1 до 12). Признак «Номер месяца» мы бинаризируем, в итоге у нас получится 12 столбцов для каждого месяца со значениями 0 или 1.

Сформируем новый датасет и посмотрим на качество модели.

Смотрим графики

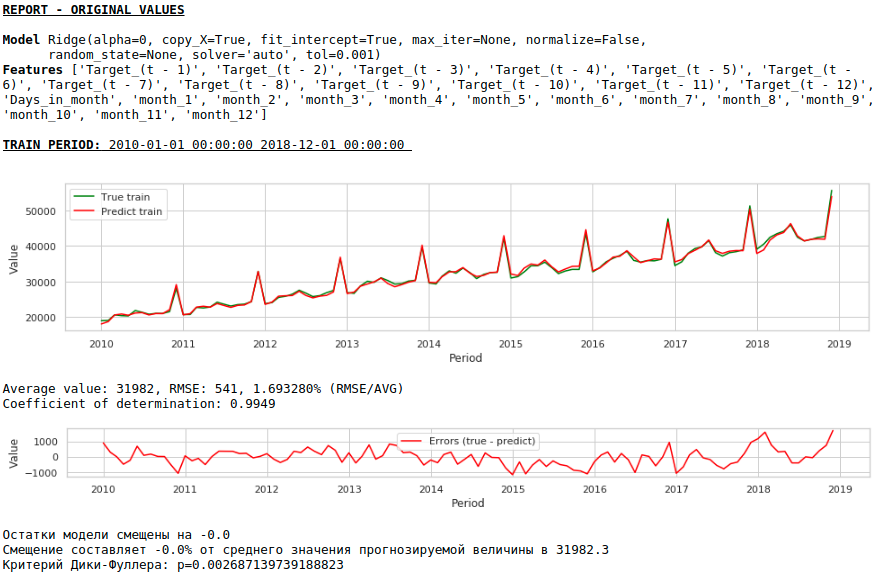
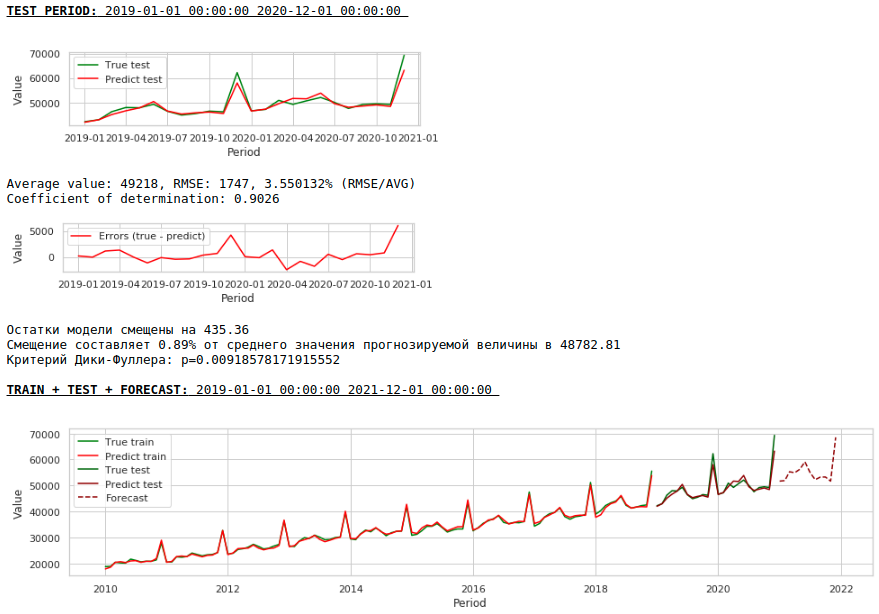
Качество получилось ниже. Визуально заметно, что прогноз выглядит не совсем правдоподобно в части роста заработной платы в декабре.

Давайте теперь проведем первую предобработку данных.

Коррекция гетероскедастичности.

Если мы посмотрим на график заработной платы за период с 2010 по 2020 гг, то мы увидим, что ежегодно разброс заработной платы внутри года между месяцами растет.

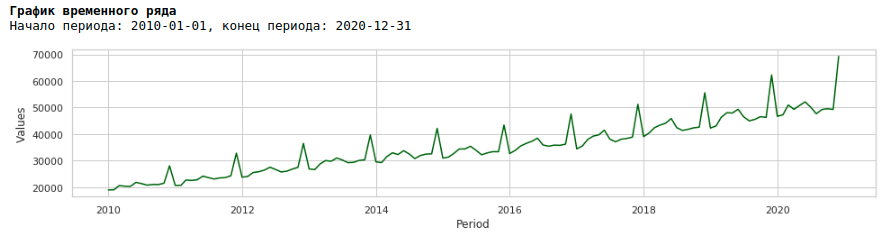
Ежегодный рост дисперсии от месяца к месяцу приводит к гетероскедастичности. Для улучшения качества прогнозирования нам следует избавиться от этого свойства данных и привести их к гомоскедастичности.

Для этого воспользуемся обычным логарифмированием и посмотрим как выглядит прологарифмированный ряд.

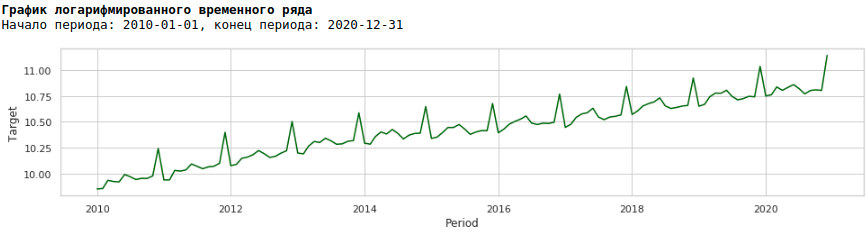
Обучим модель на прологарифмированном ряду

Смотрим графики

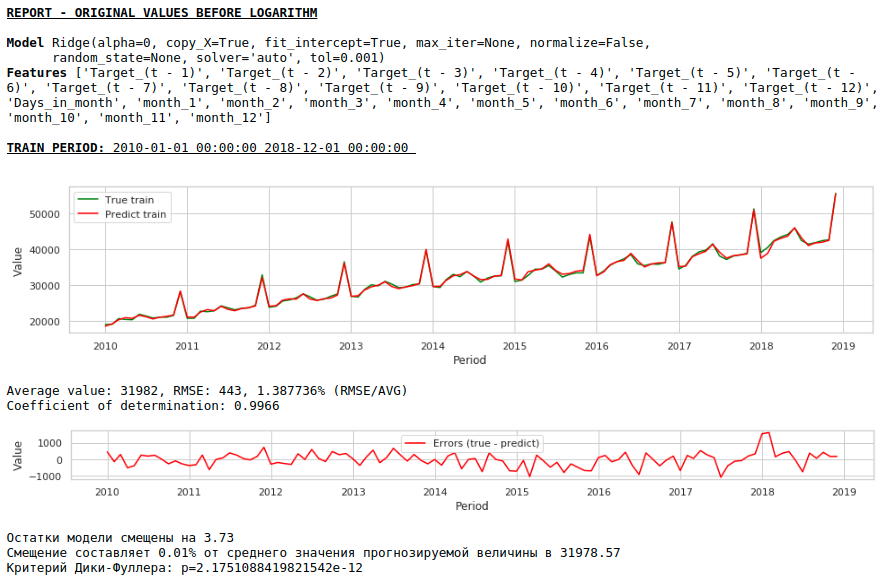
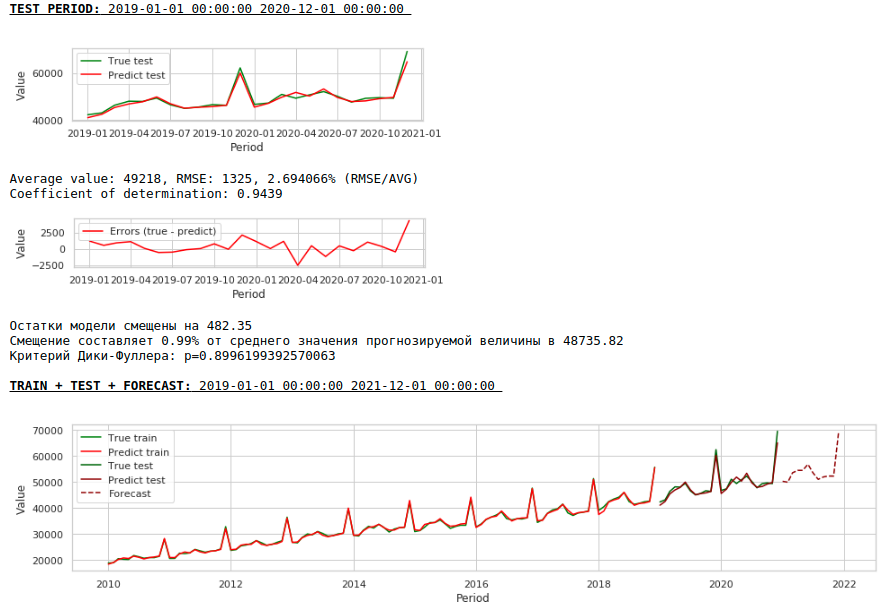
В итоге качество предсказаний на обучающей и тестовой выборках действительно улучшилось, однако прогноз на 2021 год по сравнению с прогнозом первой модели визуально выглядит менее правдоподобным. Скорее всего использование экзогенных факторов ухудшает модель.

Приведение ряда к стационарному

Приводить ряд к стационарному будем следующим образом:

Определяем разницу между целевым значением заработной платы и значением год назад: t — (t-12) = dif_1
Определяем разницу между полученным и смещенным на 1 месяц значением: dif_1 — (dif_1–1) = dif_2

В итоге получаем следующий временной ряд.

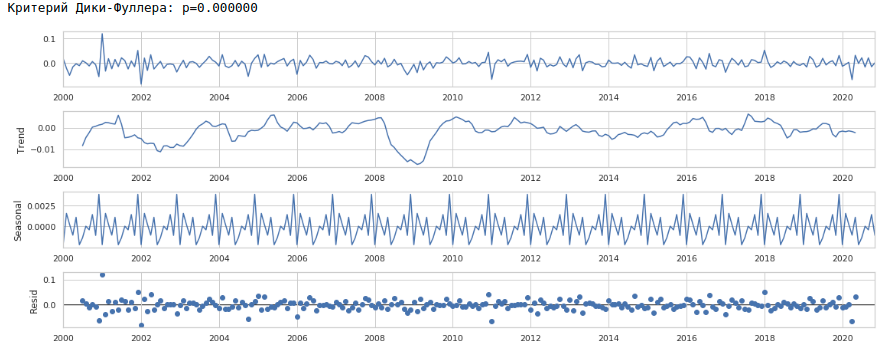
Ряд действительно выглядит стационарным, об этом также говорит значение критерия Дики-Фуллера.

Ожидать хорошее качество предсказаний на обучающей и тестовой выборках на обработанных данных, то есть на стационарном ряду не приходится, так как по сути, в этом случае модель должна предсказывать значения белого шума. Но нам, для прогнозирования заработной платы, уже совсем не обязательно использовать регрессию, так как, приводя ряд к стационарному, мы по-простому говоря, определили формулу аппроксимации целевой переменной. Но мы не будем отходить от канонов и воспользуемся регрессионной моделью, к тому же у нас есть экзогенные факторы.

Давайте посмотрим, что получилось.

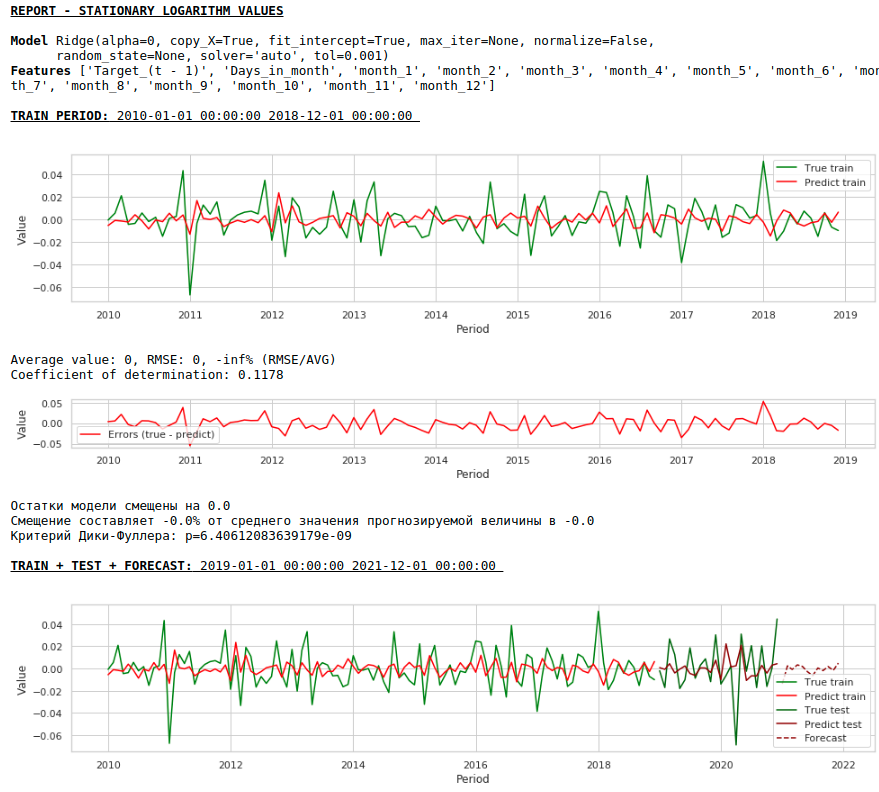
Вот так выглядит предсказание стационарного ряда. Как и ожидали — не очень-то и хорошо :)

А вот предсказание и прогноз заработной платы.

Смотрим графики

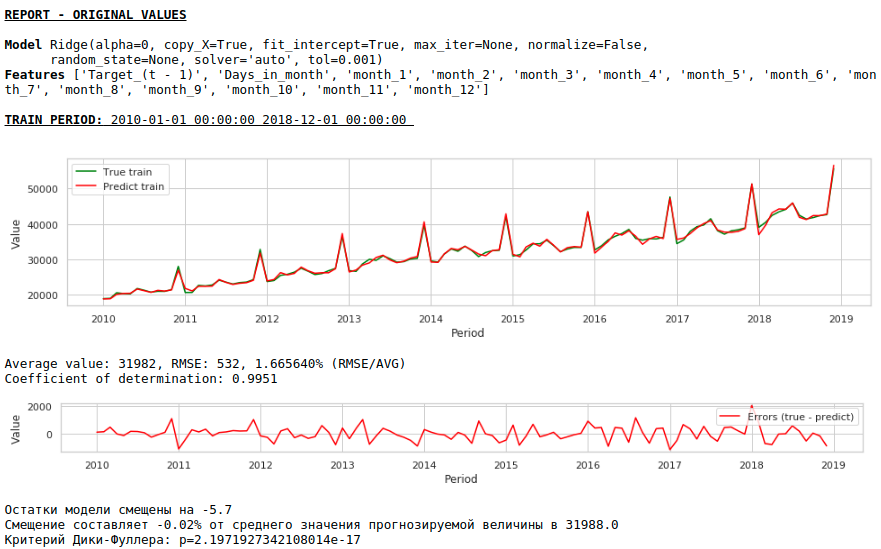
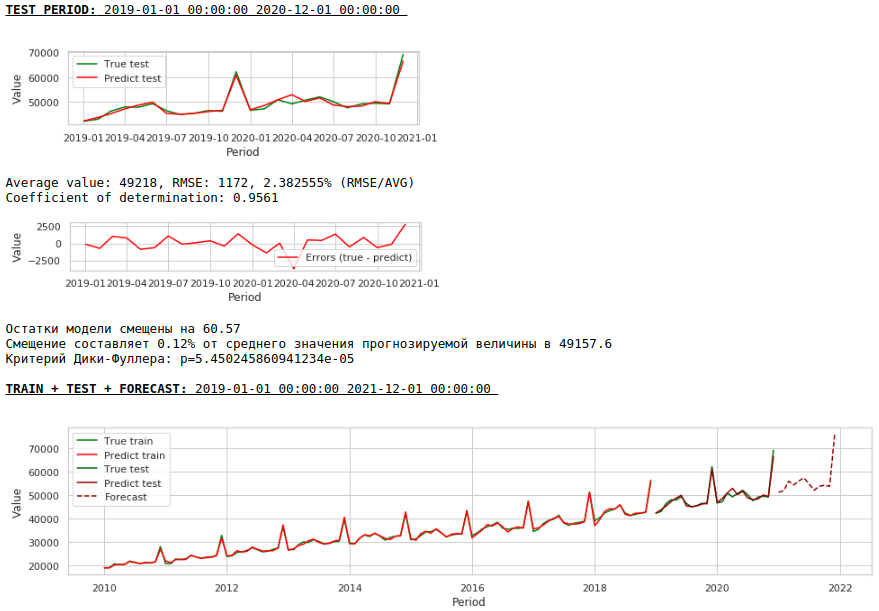
Качество заметно улучшилось и прогноз визуально стал выглядеть правдоподобным.

Теперь сформируем прогноз без использования экзогенных переменных

Смотрим графики

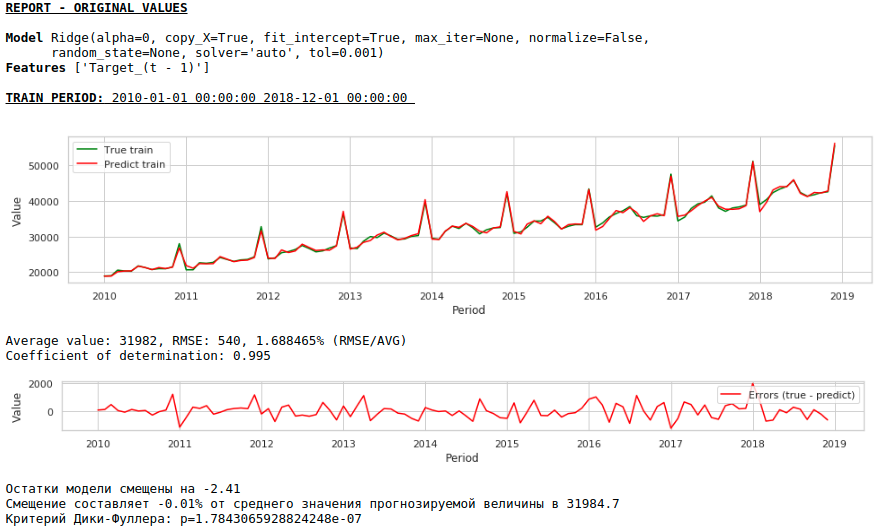
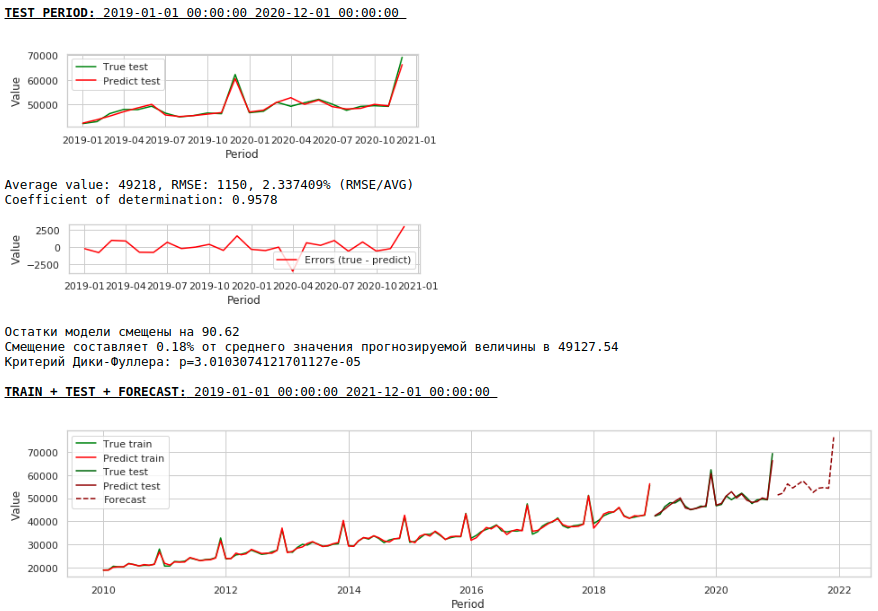
Качество еще улучшилось и правдоподобность прогноза сохранилась :)

Прогнозирование с помощью однослойной нейронной сети

На вход нейронной сети будем подавать имеющиеся датасеты. Так как наша сеть однослойная, то по сути это и есть та же самая линейная регрессия с незамысловатыми модификациями и ожидать сильно большую разницу в качестве предсказаний не стоит.

Для начала посмотрим на саму сеть

Смотрим код

class Model_1(nn.Module):
    def __init__(self, input_size, output_size):
        super(Model_1, self).__init__()
        self.input_size = input_size
        self.output_size = output_size
        self.linear = nn.Linear(self.input_size, self.output_size)
        
    def forward(self, x):
        output = self.linear(x)
        return output

Теперь пару слов о том, как будем ее обучать.

Фиксируем random seed для целей воспроизводимости результата
Инициализируем модель
Задаем функцию потерь — MSELoss
Выбираем в качестве оптимизатора Adam optimizer
Указываем начальный шаг обучения и определяем условие, при котором шаг понижается. Отмечу, что правильный выбор шага и его дальнейшее изменение (обычно уменьшение) приносит хорошие плоды
Указываем количество эпох обучения
Запускаем обучение
На вход сети подаем целиком датасет, так как он очень маленький и разбивать его на батчи не имеет смысла
При обучении, каждую тысячу эпох формируем графики значения функции потерь на обучающей и тестовой выборках. Это позволяет нам контролировать переобучение или не дообучение модели.

Ниже приведен код обучения сети на первом датасете. Для каждого датасета незначительно менялись параметры: количество эпох обучения и шаг обучения.

Смотрим код

# fix the random seed
SEED = 42
random_init(SEED)

# initialization model, loss function, optimizator
model = Model_1(len(features),1)
loss_func = nn.MSELoss()
opt = torch.optim.Adam(model.parameters(), lr=5e-2)

# set the epoch numbers, initialization list for every loss after learning on epoch
epochs = 15000
losses_train = []
losses_test = []
# initialization counter for calculation epoch numbers
counter = 0
# start the learning model
for epoch in range(epochs):
    model.train()
#     make prediction targets on train data
    y_pred_train = model(torch.tensor(X_train.to_numpy(), dtype=torch.float))
#     calculate loss
    loss = loss_func(y_pred_train, 
                     torch.reshape(torch.tensor(y_train.to_numpy(), dtype=torch.float),(-1,1)))
#     bacward loss to model and calculate new parameters (coefficients) with fixed learning rate
    loss.backward()
    opt.step()
    opt.zero_grad()

# add loss to list losses 
    losses_train.append(loss)
    
    model.eval()
    y_pred_test = model(torch.tensor(X_test.to_numpy(), dtype=torch.float))
    loss_test = loss_func(y_pred_test, 
                     torch.reshape(torch.tensor(y_test.to_numpy(), dtype=torch.float),(-1,1)))
    losses_test.append(loss_test)
    
    
# make the mini report for every 1000 epoch    
    if epoch % 1000 == 0 and epoch > 0:
        print ('Epoch:', epoch // 1000)
        print ('Learning rate:', opt.param_groups[0]['lr'])
        print ('Last loss on TRAIN data:', losses_train[-1].cpu().detach().numpy(),
              '              Last loss on TEST data:', losses_test[-1].cpu().detach().numpy())
#         print ('Last loss on TEST data:', losses_test[-1].cpu().detach().numpy())
        fig, (ax1, ax2) = plt.subplots(1, 2)
#         fig.suptitle('MSE on TRAIN & TEST DATA')
        fig.set_figheight(3)
        fig.set_figwidth(12)
        ax1.plot(np.arange(counter,epoch,1), np.array([float(i) for i in losses_train][-1000:]), color = 'darkred')
        plt.xlabel("Epoch")
        plt.ylabel("Loss on TRAIN data")
        ax2.plot(np.arange(counter,epoch,1), np.array([float(i) for i in losses_test][-1000:]), color = 'darkred')
        plt.xlabel("Epoch")
        plt.ylabel("Loss on TEST data")
        plt.show()
        
        counter += 1000
        
#   reduce learning rate
    if epoch == 1000:
        opt = torch.optim.Adam(model.parameters(), lr=7e-3)

Не будем рассматривать качество предсказаний для каждого датасета отдельно (желающие могут посмотреть подробности на гите). Давайте сравним итоговые результаты.

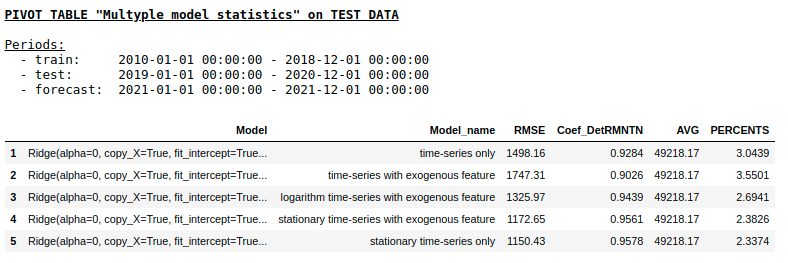
Качество на тестовой выборке с использованием Ridge Regression

Качество на тестовой выборке с использованием Single layer NN

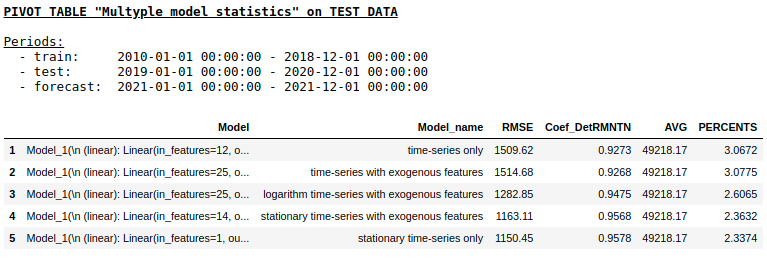
Как мы и ожидали, принципиальной разницы между обычной регрессией и простой однослойной нейронной сетью не оказалось. Конечно, нейронки дают больше маневра для обучения: можно менять оптимизаторы, регулировать шаги обучения, использовать скрытые слои и функции активации, можно пойти еще дальше и использовать рекуррентные нейронные сети — RNN. К слову, лично мне не удалось получить вменяемого качества в данной задаче с использованием RNN, однако на просторах интернета можно встретить много интересных примеров прогнозирования временных рядов с использованием LSTM.

На этом моменте статья подошла к завершению. Надеюсь, материал будет полезен как некий обзор baseline-подходов, применяемых при прогнозировании временных рядов и послужит хорошим практическим дополнением к курсу «Прикладные задачи анализа данных» от МФТИ и Яндекс.

Полезные ссылки

Исходники на гитхабе
Курс «Прикладные задачи анализа данных» от МФТИ и Яндекс
Государственная статистика «ЕМИСС» (данные по заработной плате)
LSTM for time series prediction
Лекция 9. Прогнозирование на основе регрессионной модели. Computer Science Center
Картинка под заголовком взята отсюда :)