Возможно ли мгновенная передача информации? Эксперименты с квантово запутанными частицами
Доброго времени суток всем!
Мы продолжаем рассматривать возможности квантовой механики для передачи информации с использованием корреляции квантово-запутанных частиц. В отличие от классических способов связи, использование квантово запутанных частиц дает потенциальную возможность мгновенно передавать информацию на большие расстояния. Трудность заключается в том, чтобы найти способы кодирования и декодирования передаваемой информации. Данная статья посвящена поиску решений данной задачи и возможности создания экспериментальной установки. Если вас тоже интересует данная задача — добро пожаловать под кат!
Напомню, что в прошлой статье мы рассматривали одну из возможных схем для передачи информации между двумя удаленными объектами. В частности была рассмотрена оптическая схема со светоделителями для получения интерференции, а также схема детектирования и квантового стирания с использованием двух даун-конверторов. В комментариях было множество обсуждений по поводу работоспособности такой схемы, а также критика со стороны хабрапользователей, что применение даун-конверторов приводит к взаимодействию с исходной частицей, сдвигу фаз интерференционного паттерна и прочим неприятным последствиям. Я не исключаю такой возможности, поэтому после детального рассмотрения решил исключить использование даун-конверторов и построить схему с использованием круговых и линейных поляризаторов. Забегая вперед, могу сказать, что у данного решения есть свои трудности, вследствие которых невозможно получить картину интерференции. Для решения этих трудностей мы применим элегантный подход, вытекающий из следствия самой квантовой механики. Я глубоко благодарен всем, кто участвовал в обсуждении прошлой статьи. Ваши доводы и критика помогли мне глубже понять сопутствующие трудности, искать больше информации и находить новые решения.
Для начала рассмотрим реальную экспериментальную установку. Луч лазера попадает на нелинейно-оптическое устройство: кристалл бета-бората бария (BBO), благодаря которому один фотон преобразуется в два запутанных фотона более низкой частоты. Процесс, известен как спонтанное параметрическое рассеяние. Полученная пара фотонов следуют разными путями, один из которых поступает непосредственно на детектор 1, а второй проходит через двойную щель и попадает на детектор 2. Оба детектора подключены к схеме совпадений, гарантируя, что будут учитываться только запутанные пары фотонов. Шаговый двигатель перемещает второй детектор и сканирует целевой область, создавая карту интенсивности, которая формирует знакомую картину интерференции.
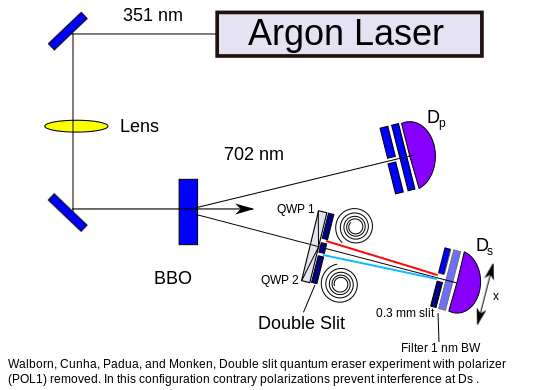
Для фотона, проходящего через двойную щель перед каждой щелью помещаются круговые поляризаторы, создающие поляризацию света по часовой стрелке при прохождении одной щели, и поляризацию против часовой стрелки при прохождении другой щели. Фотоны проходящие через поляризатор по часовой стрелке не могут пройти через поляризатор направленный против часовой стрелки. А фотоны проходящие через поляризатор против часовой стрелки, не могут пройти через поляризатор направленный по часовой стрелке. Круговые поляризаторы «маркируют» фотоны, разрушая интерференционную картину на втором детекторе (Законы Френеля-Араго).
Далее вводится линейный поляризатор на пути первого фотона, позволяющий получить диагональную поляризацию фотонов. Запутывание обеспечивает также дополнительную диагональную поляризацию в своем партнере, которая проходит через двойную щель. Это меняет эффект круговых поляризаторов — теперь каждый фотон способен пройти через круговые поляризаторы по часовой стрелке и против часовой стрелки. Таким образом, больше невозможно определить по какому пути прошли фотоны, и интерференционные полосы восстанавливаются.
Рассмотрим это подробнее на следующем примере. Представим себе Алису, использующую линейную или круговую поляризацию на первом детекторе мгновенно влияя на результаты измерения Боба на втором детекторе. Предположим, что кристалл BBO производит следующее состояние:

Если Алиса помещает круговой поляризатор перед детектором, который отфильтровывает фотоны с поляризацией по часовой стрелке, то каждый раз, когда Алиса измеряет фотон, соответствующий фотон Боба обязательно имеет поляризацию по часовой стрелки:

Поскольку Боб разместил возле каждой щели противоположные поляризационные фильтры, мы знаем, что эти фотоны могут пройти только (скажем) первую щель. Из этой щели они попадают на экран в соответствии с волновой функцией:

где a — расстояние между прорезями, d — расстояние от щелей до экрана, а x — расстояние до середины экрана. Интенсивность света на экране (количество фотонов) будет пропорциональна квадрату амплитуды этой волны, другими словами

Аналогично, когда Алиса измеряет фотон с поляризацией против часовой стрелки, соответствующий фотон Боба оказывается поляризованным против часовой стрелки, который может проходить только через вторую щель и попадать на экран с волновой функцией

Обратите внимание, что единственным отличием является знак a / 2, потому что фотон испускался из другой щели. На экране мы также увидим пятно, —, но это другое пятно, который сдвинут на расстояние a. Здесь есть один важный момент: если Боб никогда не узнает, какую поляризацию применила Алиса, то Боб на самом деле видит на своем экране сумму двух интенсивностей:

поскольку оба они производятся в равных количествах кристаллом. Боб может различать только два пика в своих данных. Только после получения результатов измерения Алисы он сможет увидеть, что для набора фотонов, где Алиса измерила поляризацию по часовой стрелке, подмножество фотонов Боба распределилось согласно 
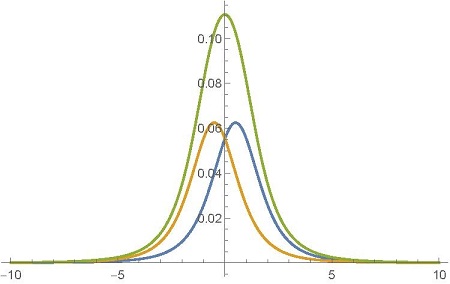
(два пика и их сумма, когда Алиса измеряет поляризацию фотонов с помощью кругового поляризатора)
Теперь рассмотрим ситуацию, когда Алиса будет использовать линейный поляризатор вместо кругового. Первое, что нужно сделать, это записать волновую функцию системы в терминах состояний линейной поляризации:


При использовании Алисой горизонтального поляризатора, волновая функция фотонов Боба окажется в состоянии суперпозиции поляризации по часовой стрелке и против часовой стрелки. Это означает, что фотон действительно сможет проходить через обе щели! При попадании на экран мы получим амплитуду волны

и его интенсивность

где

, а интенсивность

И снова на экране возникает интерференционная картина, но она слегка изменилась от предыдущего из-за разности фаз фотонов, пересекающих горизонтальный и вертикальный поляризатор.
Так может ли Алиса послать сообщение Бобу, кодируя свое сообщения с использованием линейных и круговых поляризаторов? К сожалению нет. Так как Бобу не сообщили, какая поляризация была использована Алисой, все, что он видит, является суммой двух интерференций. Следовательно, результат,

снова является пятном.
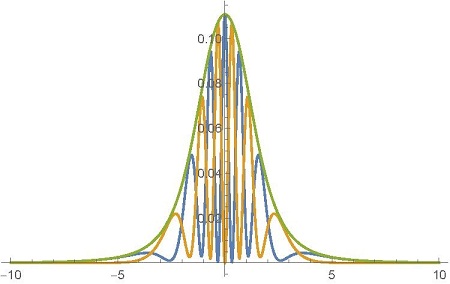
(два шаблона интерференции и их сумма, когда Алиса измеряет поляризацию фотонов с помощью линейного поляризатора)
Корреляции меняются в зависимости от того, какой эксперимент проводит Алиса. Несмотря на то, что общая картина одинакова, два подмножества в итоге дают радикально разные корреляции: если Алиса использует линейную поляризацию, то полная картина на экране формируется из двух интерференционных картин, а если Алиса использует круговую поляризацию, то картина представляет собой сумму двух пиков.
Чтобы обнаружить интерференцию потребуется изменить данный эксперимент следующим образом: вместо двух щелей с круговыми поляризаторами необходимо будет установить интерферометр Маха Цендера. Рассмотрим подробнее принцип работы данного интерферометра и попробуем узнать, что измениться при его использовании.
ИНТЕРФЕРОМЕТР МАХА ЦЕНДЕРА
На входе интерферометра находится полупрозрачное зеркало, расщепляющее световой поток на два луча. Отражаясь от двух непрозрачных зеркал они сводятся вместе во втором полупрозрачном зеркале. Будь фотон классической частицей то с вероятностью 50% он мог бы пройти через первое полупрозрачное зеркало, и с вероятностью 50% отразится от него.
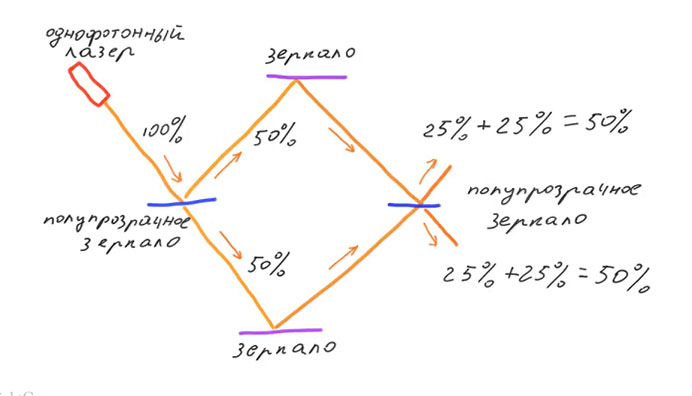
Допустим, фотон прошел первое полупрозрачное зеркало и двигается по нижней ветке. На втором полупрозрачном зеркале он также может пройти или отразиться с вероятностью 50%. То есть вклад нижней ветки таков: 25% от исходного количества фотонов будут двигаться вверх после второго полупрозрачного зеркала и 25% вниз. Если же фотон отразился на первом полупрозрачном зеркале и пошел по верхней ветке, то на втором полупрозрачном зеркале он тоже может либо пройти либо отразиться. Вклад верхней ветки также будет по 25% вверх и вниз. Общая вероятность есть сумма вкладов от двух веток и составляет 50%, что фотон будет двигаться вверх после прохождения второго полупрозрачного зеркала и 50% что вниз.
Если же провести реальный эксперимент, мы увидим, что все фотоны пройдя прибор будут двигаться вниз. Ни один фотон после второго полупрозрачного зеркала не будет двигаться вверх. Дело в том, что пройдя первое полупрозрачное зеркало фотон будет описываться не классическими вероятностями, а квантовой суперпозицией.
Обозначим базисными кет-векторами со стрелочками два возможных направления движения фотона: вверх и вниз. Тогда изначально фотон будет описываться вектором состояния «вниз». После прохождения первого полупрозрачного зеркала фотон будет в суперпозиции базисных векторов «вверх» и «вниз». Эта суперпозиция является еще одной физической реализацией кубита, наравне со спином электрона и поляризацией фотона.
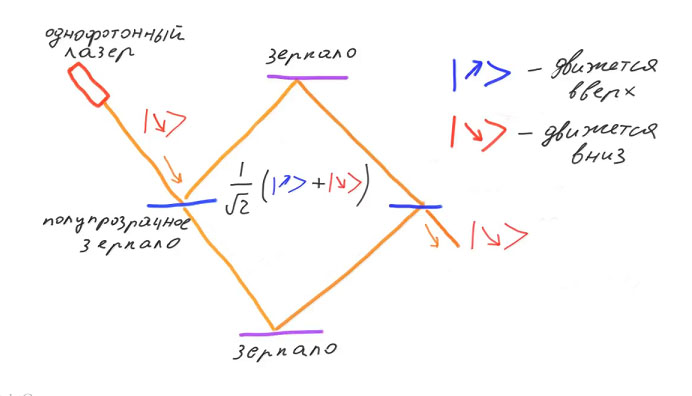
Квадраты абсолютного значения амплитуд вероятности как раз будут классические вероятности прохождения и отражения фотона. После первого полупрозрачного зеркала они будут совпадать с классическими: 50% что фотон движется вверх и 50% что вниз. После прохождения второго полупрозрачного зеркала амплитуды вероятности изменят свои значения. Причем в рамках квантовой механики можно посчитать, что одна из них будет равна нулю, а другая единице. То есть фотон вернется в состояние, описываемое базисным вектором вниз. Со стопроцентной вероятностью после прохождения второго полупрозрачного зеркала фотон будет двигаться вниз.
На выходе второго полупрозрачного зеркала наблюдается ни что иное как интерференция фотона с самим собой. Если мы попытаемся узнать по какому из плечей интерферометра действительно прошел фотон, то интерференция пропадает.
ЭКСПЕРИМЕНТ
Попробуем разместить круговые поляризаторы в интерферометре Маха Цендера. На одном плече интерферометра установим круговой поляризатор по часовой стрелке. На другом плече установим круговой поляризатор против часовой стрелки. Причем на верхнем плече круговой поляризатор устанавливается непосредственно после полупрозрачного зеркала. На нижнем плече круговой поляризатор устанавливается после отражающего зеркала. Дело в том, что фотон с круговой поляризацией отражаясь от зеркала меняет направление поляризации на противоположный. Поэтому для фотонов, которые не отразились от полупрозрачного зеркала, круговая поляризация устанавливается после отражения от зеркала.
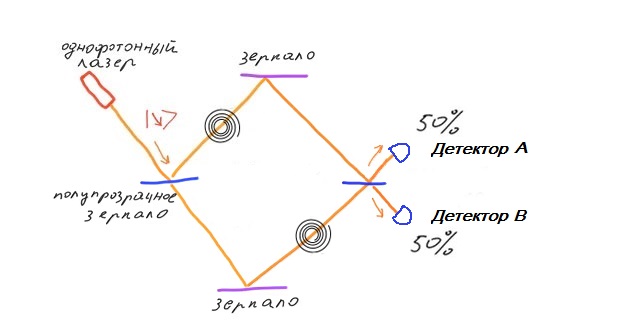
Наличие поляризаторов в интерферометре дает потенциальную возможность определить путь, по которой прошел фотон. Поэтому фотон будет проходит либо по верхнему плечу, либо по нижнему плечу, и никогда не пройдет через оба плеча одновременно. Соответственно мы не наблюдаем интерференцию на выходе. Отсутствие интерференции приводит к тому, что на выходе мы получим 50% фотонов направленных вверх и 50% фотонов направленных вниз.
Ситуация изменится, если использовать квантово-запутанные частицы. Допустим луч лазера попадает на нелинейно-оптическое устройство: кристалл бета-бората бария (BBO), благодаря которому один фотон преобразуется в два запутанных фотона более низкой частоты. Полученная пара фотонов будут следовать разными путями, один из которых проходит круговой поляризатор и попадает непосредственно на детектор 1, а второй проходит через интерферометр с круговыми поляризаторами и попадает на детектор 2 или 3.

Если на пути первого фотона разместить круговой поляризатор мы также не увидим интерференцию. Соответственно, на выходе мы получим 50% фотонов направленных вверх и 50% фотонов направленных вниз.

Но если на пути первого фотона разместить линейный поляризатор расположенный по диагонали, то запутанное состояние обеспечит дополнительную диагональную поляризацию в своем партнере. Наличие дополнительной линейной поляризации позволит фотонам пройти через оба плеча и интерферировать самим собой. При этом интерференция будет иметь разность фаз (фотоны, партнеры которых прошли через линейный поляризатор и партнеры которых не прошли, создадут на экране интерференцию, смещенный друг относительно друга). Полагаю, как и в первом эксперименте, мы не увидим интерференционных полос на выходе интерферометра. Несмотря на это, фотон на выходе из второго полупрозрачного зеркала вернется в состояние, описываемое базисным вектором вниз. Поэтому после прохождения второго полупрозрачного зеркала все фотоны будут двигаться вниз.
Такая схема реализации удобна тем, что не требует устанавливать схему совпадений запутанных частиц, выпускать фотоны поодиночке и анализировать положение каждого фотона на экране. Устанавливая или убирая линейный поляризатор на пути запутанных частиц можно моментально влиять на распределение их партнеров между детекторами 2 и 3. Достаточно сравнить интенсивность светового потока в обоих детекторах и определить передаваемый бит информации. Естественно, на выходе кристалла BBO не все фотоны получаться запутанными. Количество запутанных пар будет составлять несколько десятков процентов из общего числа. Но даже небольшое изменение интенсивности света могут быть зафиксированы детекторами, что позволит расшифровать передаваемую информацию. Второй большой плюс состоит в том, что запутанные пары не находятся в состоянии суперпозиции между собой. Это позволяет им взаимодействовать с окружающей средой и при этом не разрушать передаваемую информацию, в отличии от квантовой телепортации, когда взаимодействие с воздухом или оптическим кабелем разрушает волновую функцию фотона.
СОПУТСТВУЮЩИЕ ПРОБЛЕМЫ
Применение такой схем позволит достичь минимальной задержки при передачи информации на большие расстояния. Скорость передачи информации может существенно превосходить скорость света в вакууме. Некоторые утверждают, что СТО/ОТО запрещает передачу информации со скоростью выше скорости света. Идея конечности скорости света была предложена Пуанкаре и получена из формул Максвелла. При этом изначально речь шла об электромагнитном поле, а затем с лёгкой руки Альберта Германовича была распространена на все массивные и безмассовые материальные объекты. Важно подчеркнуть, что об информации речи не было, если открыть любую книжку по СТО/ОТО, информация не присутствует в математическом формализме. Поэтому когда утверждают о том, что СТО/ОТО запрещает передачу информации выше скорости света, делается неявное предположение, что иного способа, кроме как «посадить информацию» на пучок фотонов/электронов и т.д. не существует.
ЭНТРОПИЯ
Как мы знаем энтропия — это мера беспорядка. Считается, что течение времени приводит к увеличению энтропии. Значит, прошлое должно иметь меньшую энтропию, чем будущее. И если мы попытаемся вернуться в прошлое, то это приведет к проблеме возросшей энтропией. В действительности энтропия никак не связана с передачей информации, поскольку мы не отправляем в прошлое никакие материальные тела. Поэтому проблему возросшей энтропии термодинамических систем нельзя применять к фотонам.
ПРИНЦИП ПРИЧИННОСТИ
Одним из основных проблем мгновенной передачи информации является нарушение принципа причинности. Заметим, что современная физика нигде не требует соблюдения причинности на квантовом уровне, поэтому её среди постулатов физики нет. Существуют квантовые эксперименты, в которых стрела времени вполне может быть повернута вспять. Однако от соблюдения причинности человек пока отказаться не может, т. к. это противоречит нашей логике.
Согласно теории относительности Эйнштейна мгновенная передача информации позволяет получить информацию прежде, чем она будет отправлена. Например, если решим отправить информацию самому себе, то можем провести эксперимент таким образом, чтобы получить информацию до того, как мы его отправим. Допустим, что мы будем передавать информацию с помощью запутанной пары. Тогда один фотон пройдет через интерферометр и попадет на детектор, а второй фотон, например, отправится на Луну, где отразится от зеркала и вернется обратно к нам.
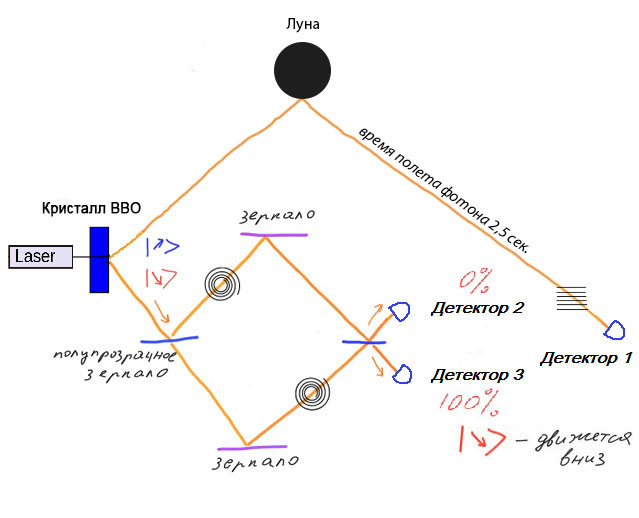
Устанавливая или убирая линейной поляризатор на пути второго фотона, мы можем влиять на результат на выходе интерферометра. Значит, наблюдая за детекторами на выходе интерферометра, мы будем заранее знать, какую информацию решим отправить через 2,5 секунды (время полета фотонов до Луны и обратно). Это может привести к «парадоксу убитой дедушки», когда мы увидели одно значение, а решили отправить противоположное.
Данную проблему позволяет решить теория альтернативных реальностей Хью Эверетта, у которого на сегодняшний день имеется много сторонников. Согласно теории Эверетта, существует бесчисленное множество альтернативных реальностей. При каждой возможности выбора наша реальность делится на несколько альтернативных реальностей, в которых реализуются все возможные варианты выбора. Реальности могут пересекаться и расходится, образуя множество вариантов прошлого и будущего.
По этой теории интерференция на двух щелях — это пересечение двух схожих реальностей без какого либо коллапса волновой функции. В одной реальности фотон проходил через первую щель, в другой реальности фотон проходил через вторую щель. При пересечении двух реальностей получается, что фотон проходил через обе щели. Мы не можем узнать через какую именно щель прошел фотон, потому что прошлое фотона для нас неопределенно. Тоже самое относится к будущему. После излучения фотона мы не можем знать где оно находится. Фотон может находится где угодно, и в каждой версии будущего реализуется один из вероятностей, где траектория фотона точно определена.
Если теория Хью Эверетта верна, то наше решение отправить противоположное значение вместо увиденного не приведет к «парадоксу убитой дедушки». В данном случае мы получим лишь среднее значение из двух возможных вариантов, по которому уже не сможем определить какую информацию решили отправить себе в будущем. Мы можем отправить любой вариант и это не приведет никаким проблемам.
Проведение реальных экспериментов, возможно, позволят нам получить экспериментальное подтверждение данной теории. Хотя косвенное подтверждение теории уже имеется. Например, существует возможность получить фотографию микроскопических объектов, не возмущая исследуемый объект (т.е. не направляя на объект ни единого фотона). Данное явление активно изучается с целью построения новых типов микроскопов.
АНАЛИЗ БУДУЩЕГО
Теория многомировой интерпретации не означает, что нет никакой возможности получить достоверную информацию из будущего. Использование вышеописанной схемы в детерминированных системах позволит получить достоверный прогноз с высокой степенью вероятности. Например, если мы решим узнать «исчезнет ли завтра Луна», то во многих альтернативных вариантах развития событий (расходящихся из нашей сегодняшней реальности) такая вероятность будет минимальна. Соответственно, результаты эксперимента будут указывать преимущественно на один вариант ответа. Можно также получить прогноз погоды с высокой степенью достоверности, минуя огромное количество вычислений в суперкомпьютерах. Возможности применения в области прогнозирования весьма велики. Одним из важных задач для анализа может выступать прогнозирование важных решений и анализ их последствий.
Следует отметить, что до реального использования в области прогнозирования будущего еще далеко. Чтобы получить задержку на сутки, потребуется вывести спутник с зеркалом на границу Солнечной системы и изготовить очень качественный лазер с минимальным углом расходимости. Если использовать многократное переотражение луча, потребуется создание идеально отражающих зеркал. Например, за сутки придется 70000 раз переотразить луч лазера между Землей и Луной. Возможно, решением станет замедление скорости света при помощи сверхохлажденной среды, известной как конденсат Бозе-Эйнштейна. Насколько мне известно, физикам из Роуландовского института научных исследований удалось замедлить скорость света до 17 метров в секунду, а через несколько лет группе ученых из Гарвардского университета удалось даже полностью остановить свет на 10–20 мс.
Источники:
Quantum eraser experiment
Интерференция кубита с самим собой
Реально ли многомирие?

