Визуализация больших графов для самых маленьких04.09.2019 14:19

rh-hypfxdji3hp8hbe5p4cdhcx8.png
Что делать, если вам нужно нарисовать граф, но попавшиеся под руку инструменты рисуют какой-то комок волос или вовсе пожирают всю оперативную память и вешают систему? За последние пару лет работы с большими графами (сотни миллионов вершин и рёбер) я испробовал много инструментов и подходов, и почти не находил достойных обзоров. Поэтому теперь пишу такой обзор сам.

Зачем вообще визуализировать графы?


Найти что искать


На входе у нас обычно просто набор вершин и рёбер, что по сути и есть граф. Мы можем посчитать по нему какие-то статистические характеристики, графовые метрики, но это не даст вам наглядную картину того, что же он из себя представляет. Хорошая визуализация может показать, есть ли в графе кластера или мосты или же он однороден, или может быть он сливается в один комок к какому-то главному центру притяжения.

Похвастаться


Визуализация данных по определению решает представительскую задачу. Если какая-то работа уже проделана, то показать выводы можно на эффектной картинке. Например, если вы делали кластеризацию графа, то можно раскрасить граф по кластерам и показать как разные метки связаны друг с другом.

Получить признаки


Несмотря на то, что алгоритмы визуализации графов в основном разрабатывались только как инструменты для получения изображений, их можно применять в качестве методов снижения размерности. Сам граф если представить его матрицей смежности — это данные в пространстве высокой размерности, а при отрисовке мы получаем две координаты для каждой вершины (иногда три, или более, но это исключение). Близость вершин на визуализации часто выражает и схожесть по свойствам.

В чём проблема с большими графами?


Под большими графами я буду подразумевать размеры, скажем, начиная от 10 тысяч вершин или рёбер. Для меньших размеров обычно никаких проблем нет, потому что почти все инструменты которые можно найти беглым поиском в интернете в основном решают свои задачи хорошо для таких объёмов. Что не так с большими графами? Проблемы две: это читаемость и скорость. Ожидаемо, что чем больше объектов, тем сложнее в них ориентироваться. Для больших графов очень часто получаются картинки, в которых невозможно разобраться. К тому же, графовые алгоритмы в основном очень медленные, многие имеют алгоритмическую сложность пропорциональную квадрату (иногда и кубу) числа вершин и/или рёбер. Даже если вы дождётесь отрисовки, то всё равно не сможете себе позволить перебирать много вариантов, чтобы получить удовлетворительный результат.

Что об этом пишут разные умные люди?


Есть пара работ, на которые я хотел бы обратить внимание:
[1] Helen Gibson, Joe Faith and Paul Vickers: «A survey of two-dimensional graph layout techniques for information visualisation»
Ребята сначала разбирают какие бывают подходы к отрисовке графов, поясняют принципы работы, а потом пытаются все их испробовать. Есть очень подробная таблица с информацией о разных алгоритмах, в том числе об их алгоритмической сложности.

[2] Oh-Hyun Kwon, Tarik Crnovrsanin and Kwan-Liu Ma «What Would a Graph Look Like in This Layout? A Machine Learning Approach to Large Graph Visualization»
Тут наши товарищи очень сильно заморочились и достали все имплементации алгоритмов визуализации графов, какие смогли. Затем визуализировали много графов и дали асессорам на разметку. По результатам научили модель оценивать на что граф будет похож в разных вариантах укладки. Из этой статьи я взял несколько картинок.

Теория


Укладка — это способ сопоставить каждой вершине графа координаты. Обычно речь идёт о координатах на плоскости, хотя вообще говоря это не обязательно должна быть плоскость. Просто использовать больше чем 2 измерения почти никогда не нужно.

Что такое хорошая укладка?


idd1jtfloxpihluaumjbjgp4t9c.png
Очень легко сказать, что что-то выглядит хорошо или плохо, но сложно объяснить машине, как такую оценку дать. Чтобы сделать «хорошую» укладку обычно оптимизируют так называемые «эстетические» метрики, которые формулируются более объективно. Вот некоторые из них:

Минимум пересечений рёбер
Всё просто: когда много пересечений, получается «каша», когда мало, тогда картинка выглядит «чище»

Смежные вершины близки друг к другу, несмежные далеки.
Граф по определению — это множество связей между вершинами и множество вершин. Сделать связанные вершины ближе друг к другу — прямой и логичный способ выразить основные свойства графовых данных.

Сообщества группируются в кластера
Это вытекает из предыдущего пункта. Если существуют множества узлов, которые сильнее связаны друг с другом, чем со всем остальным графом, они образуют «сообщество» и на картинке должны выглядеть как плотный кластер

Минимум наложений вершин и рёбер
Довольно очевидно. Если мы не сможем разобрать, один здесь объект или несколько, то визуализация читается плохо.

Распределение вершин и/или рёбер равномерно
Это условие бывает полезно если свойства графа не позволяют разглядеть хоть какую-то структуру в противном случае. Например, если у нас весь граф — это один плотный кластер, то лучше размазать его по картинке, чтобы разглядеть хотя бы неравномерность связей, чем позволить ему слиться в одно сплошное пятно.

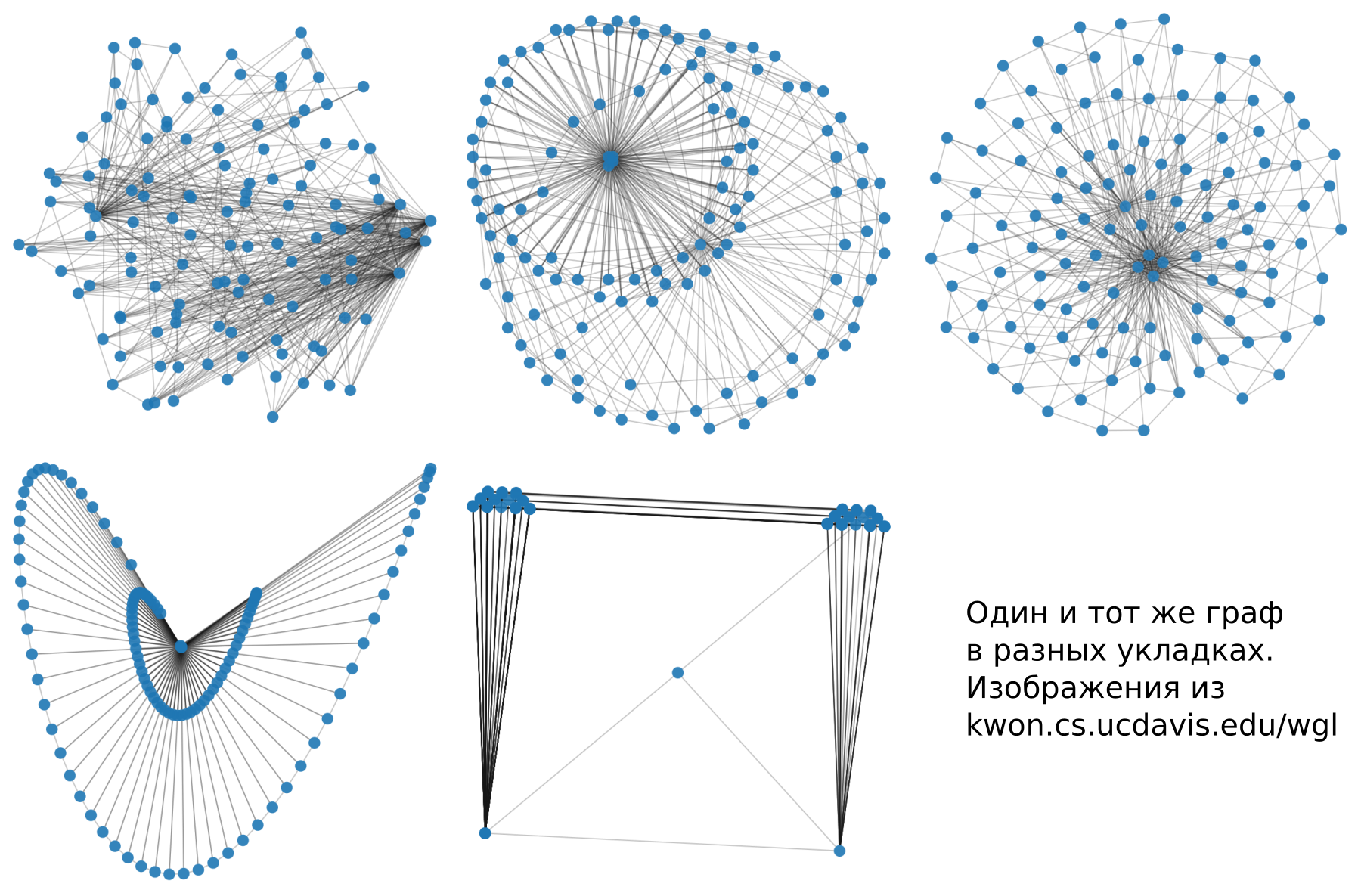
mwgt8fo1yxom-scskzhzp37nrrw.png

Какие бывают укладки


Я считаю важным рассмотреть вот эти три вида укладок, хотя классификаций и типов можно придумать много. Однако, знания этих типов достаточно, чтобы ориентироваться в предмете.

  • Force-directed and Energy-Based
  • Dimension Reduction
  • Node Features

Force-Directed and Energy-Based

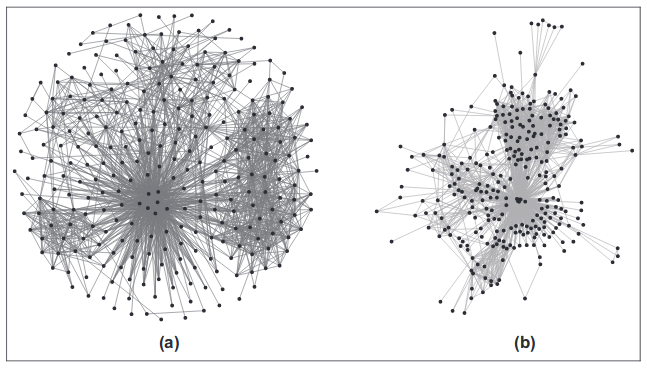
8qxfssvw7y-ouxauvilmnghb3gi.png

Эти методы используют симуляцию физических сил. Вершины представляются как заряженные частицы, которые отталкивают друг друга, а рёбра — как упругие струны, которые стягивают смежные вершины. Потом моделируется движение вершин в такой системе, пока не установится устойчивое состояние. В других подходах пытаются описать потенциальную энергию такой системы и найти положение вершин, которое будет соответствовать минимуму.

Плюсы этого семейства алгоритмов в качестве картинки. Обычно действительно получается хорошая укладка, которая отражает топологию графа. Минусы в числе параметров, которые нужно настраивать. Ну и конечно вычислительная сложность. Для каждой вершины нужно рассчитать силы действующие со стороны всех других вершин.

Важные алгоритмы семейства — Force Atlas, Fruchterman-Reingold, Kamada Kawaii и OpenOrd. Последний алгоритм — использует хитрые оптимизации, например обрубает длинные рёбра для ускорения вычислений, и в качестве побочного эффекта получаются более плотные кластера близких вершин.

Dimension Reduction

v0sh8bb4dgyko_tn6ipxzlqooqa.png

Граф можно задавать матрицей смежности, то есть квадратной матрицей NxN, где N — число вершин. Это можно интерпретировать как N объектов в пространстве размерности N. Такое представление позволяет использовать универсальные методы снижения размерности, вроде tSNE, UMAP, PCA и так далее. Другой подход основывается на том, чтобы рассчитать теоретические расстояния между вершинами, основываясь на весах рёбер и знании локальной топологии, а затем попытаться сохранить соотношения между этими расстояниями при переходе в пространства меньшей размерности.

Feature-Based Layout

kofkfsrmynrjq0p3kv-ldqyuhea.png

Обычно, данные приходят из реального мира, где у нас есть не только информация о смежности вершин. Вершины являются какими-то реальными объектами со своими свойствами. Вспоминая об этом, мы можем использовать свойства вершин для отображения их на плоскости. Для этого можно использовать любые подходы обычно применяемые для табличных данных. Это уже упомянутые выше методы снижения размерности PCA, UMAP, tSNE, Autoencoders. Либо можно рисовать простой scatter plot (диаграмма рассеяния) для пар признаков и рисовать рёбра уже поверх полученного представления. Отдельно можно упомянуть Hive Plot — интересный метод когда значениям признака соответствуют разные оси направленные из центра, на которых располагают вершины, а рёбра рисуют дугами между ними.

Инструменты для визуализации больших графов


285d0801b6c8e1e11f0cc5ba2e9bd89c.jpg
Несмотря на то, что задача визуализации старая и относительно популярная, с инструментами для больших графов большие проблемы. Большинство из них не поддерживаются. Почти каждый имеет какие-то свои тяжёлые недостатки, с которыми приходится мириться. Я расскажу только о тех, которые достойны упоминания и могут использоваться для больших графов. Для маленьких же графов никаких проблем нет — инструменты легко ищутся и в основном неплохо работают.

GraphViz


wueb-pspug6lrnbpzxjhyh7hi7e.png
Транзакции и адреса блокчейна биткоина до 2011-го года

yevaz9a9hr2z7byqvv0xpjt-wwk.png
Настроить параметры бывает сложно

Олдскульный CLI инструмент со своим языком описания графов — dot. На самом деле это пакет с разными укладками на любой случай жизни. Для больших графов там есть инструмент sfdp — относится к классу Force Directed укладок. Преимущества и недостатки этого инструмента в запуске из командной строки. Это очень удобно для воспроизводимости и автоматизации, однако без ползунков и отображения промежуточных результатов настройка параметров становится очень болезненным делом. Ставим параметры, запускаем, ждём без прогрессбара, смотрим результат, меняем параметры, перезапускаем. Умеет писать в svg, png и другие картиночные форматы.

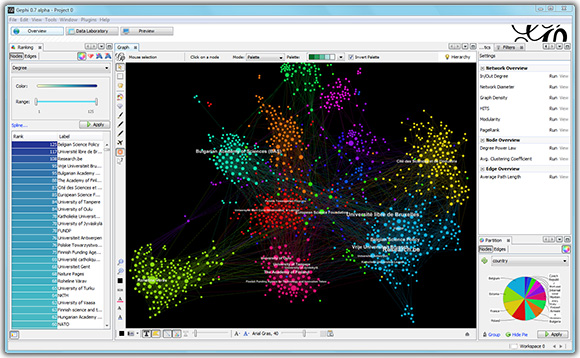
Gephi


4yk_mslprvhi9oodrdtqnxx-yfq.png
myvi8ha3zy9gdywyrlwb2vbrxmo.png
Рекомендации 173 тысяч фильмов с iMDB

vm5smc6reoeuuhdfebz2jzzvux4.png
Несколько миллионов вершин — уже слишком тяжёлая задача

Пожалуй, самый мощный инструмент по своей полноте. Это GUI приложение, которое содержит в себе набор основных укладок, а также множество других инструментов для анализа графов. Сообществом для gephi написано много плагинов, например мой любимый Multigravity Force-Atlas 2 или плагин для экспорта укладки в интерактивную веб-страницу. Также оригинальная имплементация OpenOrd содержится именно в Gephi. В Gephi есть инструменты раскраски вершин и рёбер по их свойствам, настройка подписей, размеров и прочих параметров отрисовки. Есть экспорт в основные форматы изображений, включая векторные.

Очень досадный факт в том, что Gephi уже несколько лет заброшен. Два основных разработчика, не обладают ресурсами чтобы передать свои знания, необходимые для дальнейшей разработки кому-то ещё, заявили что уже не могут больше активно поддерживать Gephi. К другим минусам можно отнести некоторую «дубовость» интерфейса, и отсутствие каких-то очевидных фич, но ничего «подобного только лучше» всё равно никто не написал. Из последних новостей, в блоге проекта появилось заявление о том, что мощности современного WebGL уже обгоняют старый Gephi и есть шансы увидеть его возрождение в виде веб-приложения.

igraph


gidp0gtrx_3wuweqy38htprwr88.png
Граф рекомендаций музыки в lastfm. Источник здесь.

Нельзя не отдать дань этому пакету общего назначения для анализа графов. Одна из самых эффектных графовых визуализаций своего времени была сделана одним из авторов igraph. Он разработал для этого свою укладку DrL. Это был граф рекомендаций музыкальных групп из lastfm. Результат ниже.

К минусам можно отнести отвратительную документацию. Как минимум к python api. Проще сразу читать исходники.

LargeViz


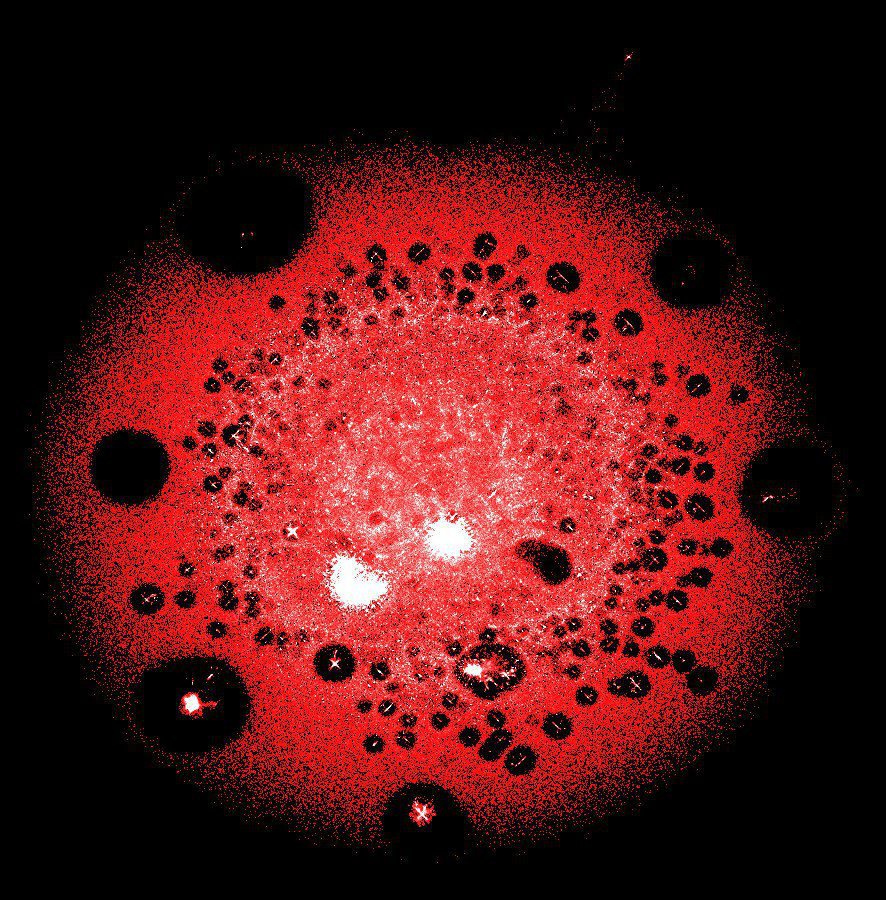
pbzsei2xlducda9zyrfxq28byie.png
Несколько десятков миллионов вершин (транзакций и адресов) в одном из крупнейших кластеров блокчейна биткоина

Настоящее спасение, когда нужно отрисовать гигантский граф. LargeViz относится к алгоритмам снижения размерности и может применяться не только для графов, но и для произвольных табличных данных. Работает из командной строки и отличается великолепной производительностью. Очень экономный по памяти и быстрый.

Graphistry


cdrlwjahosvqugbdaau5gjknfws.png
Адреса, которые можно взломать за неделю, и их транзакции

q7sqylxv6mblsvrvp8vvbe5vtxu.png
Понятный, но очень ограниченный интерфейс, разумные настройки по умолчанию

Единственный в этом списке коммерческий инструмент. Graphistry — это сервис, который принимает ваши данные и выполняет тяжёлые вычисления на своей стороне. Клиент просто смотрит на красивую картинку в браузере. По сути ничем не лучше gephi, кроме разумных параметров по умолчанию и интерактивности. Реализует только одну укладку: что-то похожее на ForceAtlas. Есть ограничение 800 тысяч на максимальное число вершин или рёбер.

Графовые эмбеддинги


Для безумных размеров тоже есть свой подход. Уже начиная с миллиона вершин при отрисовке имеет смысл смотреть только плотность вершин в разных точках пространства, просто потому что ничего другого увидеть не выйдет. Большая часть алгоритмов придуманных специально для отрисовки графов, на десятках миллионов вершин или рёбер будет работать по много часов, если не суток. Из этой ситуации можно выйти решая немного другую задачу. Есть множество методов получения векторных представлений заданной размерности, отражающих свойства вершин графа. После получения таких представлений остаётся только снизить размерность до 2-х, чтобы получить уже картинку.

Node2Vec


1ty8ewo6mmifh_l5qbeda7jjpai.png
Node2Vec + UMAP

Адаптация обычного word2vec для графов. Вместо последовательностей слов берутся последовательности вершин при случайном обходе графа и отправляются в word2vec вместо слов. Метод учитывает только информацию о соседстве вершин. Обычно этого достаточно.

VERSE


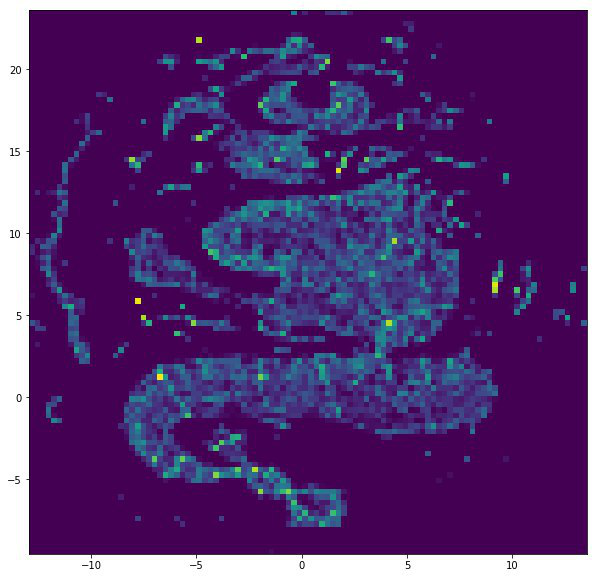
g3arcswamviboy1udut3wn7qqiq.png
VERSE + UMAP

Продвинутый алгоритм для получения графовых эмбеддингов, который стремится получить разностороннее представление для вершин, то есть учесть все роли, которые вершина принимает в графе. Учитывается и соседство вершин и локальная топология графа.

Graph Convolutions


rh-hypfxdji3hp8hbe5p4cdhcx8.png
Graph Convolutions + Autoencoder

Существует много способов определить операцию свёртки на графах, но по сути это «размазывание» информации по графу, так чтобы вершины получали информацию о признаках своих соседей. В эти признаки можно добавить и информацию о локальной топологии.

Бонус: немного подробнее о графовых свёртках


Все описанные подходы опираются на какие-то готовые инструменты. Последний случай — исключение. Чтобы реализовать графовые свёртки, нужно немного подумать и написать чуть-чуть кода.

Подробный разбор свёрток на графах и прочих неевклидовых данных — тема достойная отдельной статьи. Здесь я опишу простейший базовый подход, который не требует специальных графовых фреймворков и легко масштабируется. Итак, мы хотим, чтобы признаки каждой вершины графа содержали информацию о признаках соседей.

Как нам это сделать?


Самый очевидный способ — просто взять среднее по соседям. Если ещё немного порассуждать о том, какие бывают случаи и какую информацию теряет среднее, туда можно добавить прочие статистики, вроде стандартного отклонения, минимума, максимума и так далее.

Как теперь это организовать? Начнём с того, что граф — это по сути множество вершин и множество рёбер. Нас интересуют только связные куски больше чем из одной вершины, поэтому список рёбер в нашем случае полностью определяет граф. Это удобно записать в виде таблицы: в первом столбце вершины из которых выход/т ребро, во втором, куда эти рёбра входят. Дальше нам нужно считать статистики. Это очень общая задача и поэтому можно воспользоваться фреймворками, в которых всё до нас максимально оптимизировано.

Мощь табличных фрейморков в анализе графов


Мы пришли к тому, что у нас есть табличка задающая граф и нам надо считать статистики по каким-то величинам. Таблицы и статистики — это всё есть в pandas, поэтому дальше будет пример реализации именно в нём.

Для начала зададим граф: 

ara = np.arange(101).reshape(-1, 1)
sample = np.vstack((np.hstack((ara[:-1], ara[1:])), # forward links
                    np.hstack((ara[1:], ara[:-1])))) # backward links


Это просто цепочка из 101 вершины связанных друг за другом, как на рисунке.
oxantsns3bhlqlse-xsusotsimg.png

Затем зададим признаки вершин случайным образом: 

feats = np.random.normal(size=(101, 10))

И сделаем из этого всего датафреймы pandas: 

edges = pd.DataFrame(sample, columns=['source', 'target'])
cols = ['col{}'.format(i) for i in range(10)]
feats = pd.DataFrame(feats, columns=cols)
feats['target'] = ara


Теперь зададим саму функцию свёртки: 

def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean',
                      prefix='mean_'):
    """
    edges -- edgelist: pandas dataframe with two columns (arguments by and on)
    feats -- features dataframe with key column (argument on) 
             and features columns (argument cols)
    by -- column in edges to be used as source nodes
    on -- column in edges to be used as neighbor nodes
    size -- number of unique source nodes to be used in one chunk
    agg_f -- can be interpreted as pooling function. 
             Pandas has several optimised functions for basic statistics,
             that can be passed as string arg (see pandas docs),
             but you also can provide any function you like
    prefix -- prefix for new column names             
    """
    res_feats = [] # used to stack result chunks

    # get chunk of unique source nodes
    for chunk in tqdm(chunker(edges[by].unique(), size=size), 
                      total=(len(edges[by].unique()) // size) + 1):
        # for each chunk we get feature matrix for neighbours
        temp = edges[edges[by].isin(chunk)]\
                .merge(feats, on=on, how='left')
        # convolve and pool
        tempgb = temp[cols + [by, on]]\
                .groupby(by).agg({col: agg_f for col in cols}).reset_index()
        res_feats.append(tempgb.rename(columns={c: prefix + c for c in cols}))
    # concat results
    return pd.concat(res_feats, axis=0).reset_index(drop=True)

Что тут происходит:


Сначала мы выбираем кусок вершин для которых будем делать свёртку, берём все их рёбра, конкатенируем его с признаками соседей и записываем в датафрейм temp. Затем группируем по вершинам источникам, и аггрегируем, применяя функцию agg_f, которая по молчанию просто среднее. Добавляем резльтат для текущего куска в список, и в конце просто конкатенируем результаты.

1fk3k65sqmjcnfwgfe9nqmb2wku.png
Для данного графа это будет выглядеть так

Применяем функцию и рисуем результат: 

conv1 = make_conv(edges, feats, cols, 'source', 'target')
plt.figure(figsize=(3, 8))
plt.imshow(np.hstack((feats[cols].values,
                      conv1.values[:, 1:])), cmap='jet');

pu21sgpgddhuvgslpsgw4hguvvg.png
Исходные признаки, затем исходные и результат первой свёртки, затем исходные и результат двух свёрток.

Для примера был специально выбран такой простой случай, чтобы легко было визуально увидеть, как признаки «размазываются» по соседям, если напрямую нарисовать матрицу признаков. В более общем случае процесс выглядит примерно так:
jcvz9ybg9t_8zfl20_xhf6ebem8.png

Если хочется немного больше математики


Если вы раньше слышали про графовые свёртки, то скорее всего это было в контексте графовых свёрточных сетей (Graph Convolutional Networks — GCN). Кому-то фокусы с табличками, которые здесь описаны, могут показаться «не тру». На самом деле, использованию графовых свёрток без глубокого обучения посвящена одна очень интересная статья: «Simplifying Graph Convolutional Networks». В ней даётся такое определение свёртки $H^{(k)} \leftarrow SH^{(k - 1)}$ где $H $ — это матрица признаков, а $S $ — нормализованный лапласиан графа, который задаётся вот так: $S = \tilde{D} ^{- \frac{1}{2}} \tilde{A} \tilde{D} ^{ \frac{1}{2}}$, здесь $\tilde{A}$ — это матрица смежности графа суммированная с единичной матрицей, а $\tilde{D}$ — матрица в диагонали которой записаны степени вершин графа. И всё это записывается парой строк в python с использоаванием scipy и numpy: 

S = sparse.csgraph.laplacian(adj, normed=True)
feats_conv = S @ feats


Здесь sparse — это модуль внутри scipy для работы с разреженными матрицами, adj — матрица смежности, а feats и feats_conv — признаки до и после свёртки. Такой подход более строгий, но очень плохо масштабируется. К тому же, если чуть-чуть вдуматься в смысл происходящего, то это эквивалентно разницы между значением признака в вершине и средним по соседям вершины, то есть вполне решается предыдущей схемой с таблицами, если добавить одну операцию.

Ссылки


Обзоры о визуализации графов
leonidzhukov.net/hse/2018/sna/papers/gibson2013
arxiv.org/pdf/1710.04328.pdf

Simplifying Graph Convolutional Networks
arxiv.org/pdf/1902.07153.pdf

GraphViz
graphviz.org

Gephi
gephi.org

igraph
igraph.org

LargeViz
arxiv.org/abs/1602.00370
github.com/lferry007/LargeVis

Graphistry
www.graphistry.com

Node2Vec
snap.stanford.edu/node2vec
github.com/xgfs/node2vec-c

VERSE
tsitsul.in/publications/verse
github.com/xgfs/verse

Ноутбук с полным кодом свёрток на pandas
github.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynb

Graph Convolutions
Здесь собраны работы о графовых свёрточных сетях: github.com/thunlp/GNNPapers

Суть всей статьи в одной таблице


© Habrahabr.ru