Устранение перспективных искажений и разгибание кривых строк на фотографиях книжных разворотов
Итак, считаем, что мы уже нашли на фотографии линию корешка, воспользуемся этим знанием, чтобы определить ваниш-точки для страниц разворота (vanishing point). Ваниш-точки — это точки схождения параллельных прямых в перспективной проекции книги на плоскость изображения. Они обе должны располагаться на продолжении этой линии, но для каждой из страниц положение точки может быть свое. Схематически это показано на следующей иллюстрации (на самом деле, это лог для отладки). Линия корешка выделена красным, линии, пересекающиеся в ваниш-точках, — зеленым.
Как правило, ваниш-точки двух страниц находятся недалеко друг от друга, но приведенный пример показывает, что так бывает не всегда: для левой страницы этого разворота зеленые линии сходятся очень слабо и ваниш-точка лежит далеко внизу, а для правой — вверху, относительно близко от края изображения.
Каким образом можно найти эти линии на изображении? На помощь нам опять-таки приходит преобразование Хафа (Hough transform), только изображение мы должны для этого подготовить соответствующим образом. Постараемся выделить границы текстовых блоков на изображении максимально простым способом. Для этого выполним следующие несложные действия:
1) Бинаризация;
2) Нормализация изображения по размерам, например до 800 пикселей по длинной стороне;
3) Морфологическое наращивание (dilation, r = 6);
4) Морфологический градиент (r = 1).
Если к полученному изображению применить быстрое преобразование Хафа, мы получим:
На нем отчетливо различимы несколько локальных максимумов, соответствующих границам страниц и текстовых блоков. Линия корешка разделяет эти множества на два (назовем их «левое» и «правое» соответственно), при этом каждое из них хорошо описывается линией в пространстве Хафа. Как известно, линиям в простанстве Хафа соответствуют точки в пространстве изображения. Это и есть искомые ваниш-точки.
Для поиска линий в пространстве Хафа предлагается сначала выделить локальные максимумы с помощью алгоритма non-maximum suppression. Отбрасываем все максимумы слабее 0.2 от наибольшего. В принципе, шум можно фильтровать и по-другому, тут важно оставить лишь точки, соответствующие достаточно протяженным контурам на изображении градиента. Группу максимумов из окрестности точки, соответствующей линии корешка (на рисунке в начале статьи она выделена красным), мы усредняем и добавляем центр этого кластера к «левому» и «правому» множествам точек с увеличенным весом. Применяем метод наименьших квадратов (МНК) для поиска линий, описывающих наши множества точек (на рисунке они выделены зеленым). Таким образом, мы получили ваниш-точки в пространстве исходного изображения. К сожалению, изобразить их на нем не получится, т. к. они лежат далеко за его пределами. Зная положения этих точек, мы нарисовали виртуальные линии, пересекающиеся в них — смотрим еще раз на первую картинку, они там выделены зеленым.
Теперь мы можем распрямить исходную картинку, исправив вертикальную перспективу на ней. Построим виртуальные четырёхугольники страниц на исходном изображении. Нам необходимо каким-то образом задать координаты четырёх углов документа, по которым мы сможем построить проективное преобразование. Стоит отметить, что такое построение не единственно, исходя их природы наблюдаемых вещей, мы выбрали следующий вариант: считаем, что наши четырёхугольники являются трапециями, их основания перпендикулярны линии корешка, которая является одной из боковых сторон, а другая боковая сторона проходит через ваниш-точку и середину боковой стороны изображения. Так, с одной стороны, мы не слишком много отрезаем от картинки, а с другой стороны, не делаем наши четырёхугольники слишком большими. Здесь для примера другая картинка, но принцип от этого не меняется:
Разумеется, можно ставить основания трапеций выше или ниже, внешние стороны сдвигать наружу или внутрь и получать при этом другие проективные преобразования, но нам на этом этапе важно лишь, чтобы корешок стал вертикальным, а строки — одинаковой длины. Применяем полученные проективные преобразования независимо для каждой из страниц, получаем:
Вертикальную перспективу можно считать исправленной. Переходим теперь к разгибанию кривых строк.
Выделяем наклонные «фрагменты» слов на изображении (а для этого картинка бинаризуется, на ней выделяются связные компоненты, строится граф, описывающий их взаимное положение, происходит предварительная сборка слов). Цвет показывает угол наклона фрагмента: если < 0 – зеленый, если > 0 — красный, равный 0 (округленно до 1 градуса) — синий.
Под «фрагментом» мы здесь понимаем «склеившиеся в слово» связные компоненты. Ему может соответствовать как слово целиком, так и какой-то фрагмент слова, это лишь результат предварительного анализа, не претендующий на истину. Можно видеть, что выделились далеко не все слова, но для построения модели страницы этого будет достаточно.
Используем следующую модель страницы:
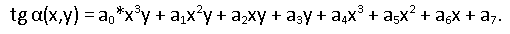
О чем нам говорит эта формула? Тангенс локального угла наклона строк является полиномом 3-й степени по горизонтали и 1-й степени по вертикали (здесь и далее используем обычные декартовы координаты на плоскости). В самом деле, если считать искажения страницы в пространстве цилиндрическими (радиус изгиба листа зависит только от координаты х), то зависимость угла наклона по вертикали при проекции на плоскость изображения будет линейной. В горизонтальном направлении мы считаем, что полином 3-й степени будет описывать меняющийся угол наклона с достаточной точностью. Разумеется, мы пробовали полиномы меньших и больших степеней. Вообще, выбор модели до некоторой степени произволен, важно чтобы она достаточно хорошо описывала наблюдаемые значения углов. А откуда мы их будем брать? Из тех самых наклонных фрагментов слов. У нас есть выборка данных по локальным углам наклона строк для страницы, у каждого фрагмента есть координаты его центра и значение угла наклона, которое мы определяем по набору склеившихся связных компонент.
Используем привычный уже МНК, чтобы найти вектор параметров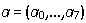 
. Далее, произведем фильтрацию выбросов, т. к. мы могли по ошибке вместо фрагмента слова выделить где-то что-то другое (анализ-то у нас был грубый, предварительный).
Здесь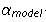 
— значение угла, вычисленное по модели в точке с координатами центра i-го фрагмента, 
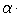— значение угла наклона самого фрагмента (исходные данные), значения углов заданы в радианах. Если в результате фильтрации у нас остается достаточное количество фрагментов, описываемых моделью с заданной погрешностью, мы можем уточнить ее, применяя МНК к оставшимся данным. Таким образом мы получаем предварительную модель страницы. Она достаточно хорошо описывает кривые строки в тех участках изображения, где у нас было выделено достаточное количество фрагментов слов, однако в области корешка решение является неточным. Если мы будем его использовать для разгибания строк, эта область будет искажена.
Попробуем с помощью нашей модели «проследить» строки до конца. Центры фрагментов слов будут служить «затравками» для алгоритма прослеживания.
Подготовим изображение для прослеживания кривых строк:
— бинаризация,
— замыкание по горизонтали (сборка строк),
— размыкание по горизонтали (избавляемся от заглавных, выносных элементов),
— гауссово сглаживание (немного размываем строки по вертикали).
Замыкание и размыкание выполняем окном шириной R = w/100, где w — ширина изображения. Сглаживание выполняем с σ = h/400, где h — высота изображения.
Прослеживаем строки, начиная из центра каждого фрагмента слова в обе стороны.
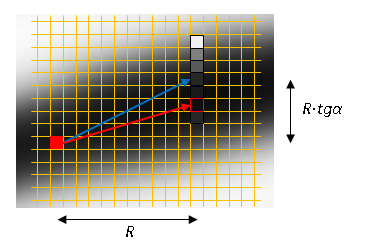
Смещаемся каждый раз на фиксированный шаг R по горизонтали и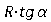 
по вертикали. Значение угла определяем по модели. Делаем поиск локального максимума в вертикальном столбце высотой ±3 пикселя. Продолжаем процесс из уточненного положения. Критерий остановки — отсутствие локального максимума или значение максимума не превосходит шумовой порог (T = 30).
В результате прослеживания получаем гораздо больше данных — отрезков с уточненным значением угла наклона. Уточняем нашу модель с использованием этих данных.
Используя полученную из модели карту углов, строим карту локальных смещений. Учитываем при этом угол горизонтальной перспективы в текущей точке:
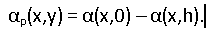
Смещение в любой точке умножаем на 
. Это позволяет «растянуть» буквы в области корешка.
► ► ► 
Получаем изображение, которое уже можно подавать на вход OCR. Для построения приятной для глаз картинки придется еще поработать. Нам хотелось бы получить что-то вроде этого:
Как это сделать (разумеется, автоматически), мы предлагаем поразмыслить читателям. В заключение отметим, что этот алгоритм уже нашел применение в мобильном приложении ABBYY FineScanner, которое теперь умеет обрабатывать фотографии книжных разворотов.
