Трехпутевая поразрядная быстрая сортировка
Сегодня речь пойдет о не самом известном алгоритме сортировки — трехпутевая поразрядная быстрая сортировка.
Этот алгоритм является гибридом широко известных быстрой сортировки и поразрядной сортировки.
Подробности — под катом.
Но для начала, вспомним старое.
Ее знает большинство. Если кратко — берем опорный элемент, обменами делаем так, чтобы с одной стороны от него в массиве остались меньшие элементы, с другой — большие либо равные. Далее запускаем рекурсивно ту же процедуру на получившихся частях. Сам опорный элемент при этом уже оказался на том месте, на котором он будет в отсортированном массиве.
При этом часто говорят об оптимизациях быстрой сортировки.
Самая известная оптимизация — выбирать опорный элемент случайным образом. Таким образом существенно уменьшается вероятность «попадания» в случай, когда быстрая сортировка показывает наихудшую производительность (О (n^2), как мы все помнят).
Вторая по популярности идея — разделять массив не на две, а на три части. Элементы меньше опорного, равные ему и элементы больше опорного. Эта оптимизация заметно ускоряет время выполнения в случаях, когда в исходном массиве много одинаковых элементов — ведь равные опорному элементы также, как и опорный, уже «попали» на свое место в отсортированном массиве, и никаких дополнительных процедур для их сортировки уже не требуется. Уменьшается и количество выполняемых операций и глубина рекурсивных вызовов. В общем, неплохой способ немного сэкономить.
Сложность — O (nlogn) в среднем, O (n^2) в худшем, доп.память — O (1)
Если что, вот тут неплохо и кратко написано.
Поразрядная сортировка (Radix Sort)Чуть менее популярный алгоритм, но достаточно хорошо известный.
Логика его работы проста. Допустим, у нас есть массив чисел.
Сначала отсортируем их по первому (старшему) разряду. Сортировка в таком случае выполняется с помощью сортировки подсчетом (count sort). Сложность — o (n). Мы получили 10 «корзин» — в которых старший разряд 0, 1, 2 и т.д. Далее в каждой из корзин запускаем ту же процедуру, но только рассматриваем уже не старший разряд, а следующий за ним, и т.д.
Шагов столько, сколько разрядов в числах. Соответственно, сложность алгоритма — O (n*k), k — число разрядов.
Есть два вида такой сортировки — MSD (most significant digit — сначала старший разряд) и LSD (least significant digit — сначала младший разряд).
LSD несколько удобнее для сортировки чисел, т.к. не приходится «приписывать» к числам слева незначащие 0 для выравнивания числа разрядов.
MSD же удобнее для сортировки строк.
Алгоритму в такой реализации требуется дополнительная память — O (n).
Прочитать подробнее можно, например, здесь.
Трехпутевая поразрядная сортировкаДопустим, мы выполняем сортировку строк.
Использовать qsort, который активно сравнивает элементы, выглядит слишком накладным — сравнение строк операция долгая. Да, мы можем написать свой компаратор, который будет несколько эффективнее. Но все же.
Использовать radix, который требует дополнительную память, тоже не слишком мотивирует — строки могут быть большими. Да и большая длина строк, т.е. число разрядов, удручающе сказываются на эффективности.
А что если как-либо образом скомбинировать эти алгоритмы?
Логика работы получившегося алгоритма такая:
1. Берем опорный элемент.
2. Разделяем массив на три части, сравнивая элементы с опорным по старшему разряду — на меньшие, равные и большие.
3. В каждой из трех частей процедуру повторяем, начиная с шага №1, до тех пор, не дойдем до пустых частей или частей с 1 элементом.
Только в средней части (т.е. где старший разряд равен старшему разряду опорного элемента) переходим к следующему разряду.
В остальных частях операция начинается без изменения «рабочего» разряда.
Сложность сортировки — O (nlogn). Дополнительная память — O (1).
Минус этого алгоритма в том, что в отличие от поразрядной сортировки, она разбивает массив лишь на три части, что, например, ограничивает возможности многопоточной реализации.
Преимущество над быстрой сортировкой в том, что нам не требуется сравнивать элементы «целиком».
Преимущество над поразрядной сортировкой — нам не нужна дополнительная память.
Отдельно стоит отметить, что такой сортировкой удобно пользоваться, когда элементом исходного массива является другой массив.
Тогда, если исходный массив input, то, например, старший разряд — input[i][0], следующий — input[i][1] и т.д.
Такая сортировка называется многомерной быстрой сортировкой, или же multikey quicksort.
Подробнее и более развернуто — Р. Седжвик, Фундаментальные алгоритмы на С++, ч.3, гл.10, 10.4 «Трехпутевая поразрядная быстрая сортировка»
Схема работы алгоритма: 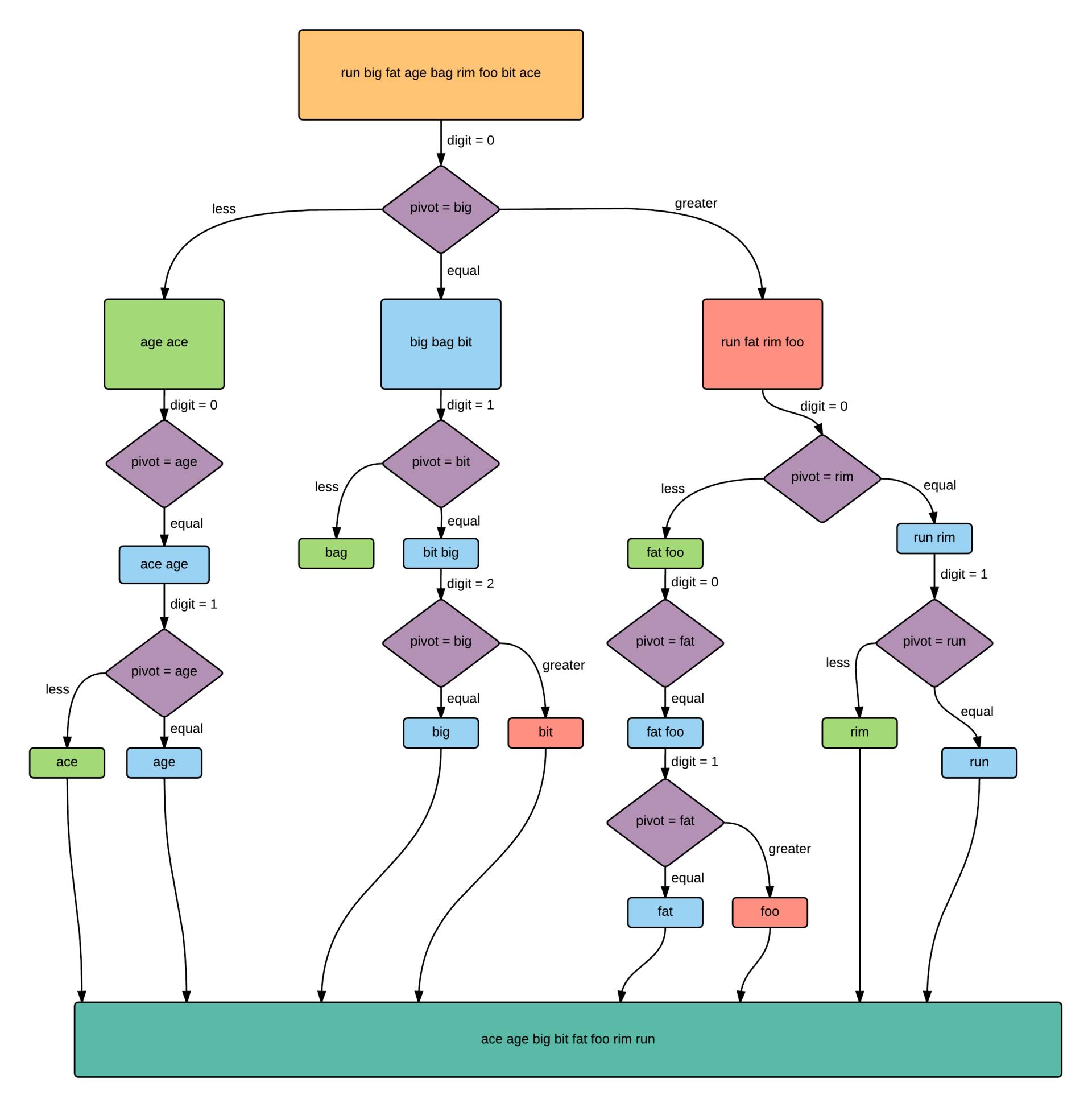
Отметим, что наиболее простой способ реализовать разделение массива на три части относительного опорного — использовать алгоритм Бентли и Макилроя.
Он заключается в том, что в стандартную процедуру разделения qsort вносится следующее дополнение (непосредственно после обмена элементов).
Если обработанный элемент попал в левую часть массива (т.е. он не больше опорного) и он равен опорному, то он помещается в левую часть массива путем обмена с соответствующим элементом (который уже был полностью обработан и соответственно, меньше опорного).
Аналогично, если обработанный элемент попал в правую часть массива и равен опорному, то он помещается в правую часть массива.
После завершения процедуры разделения, когда количество элементов меньше опорного уже точно известно, выполняется перенос равных элементов в середину массива (сразу после элементов, меньших опорного).
Подробно о нем можно прочитать в Р. Седжвик — Фундаментальные алгоритмы на С++, ч.3, гл.7, п.7.6 «Дублированные ключи».
