Типичные задачи аналитика данных. Часть 1. Упала метрика
В прошлой статье мы рассматривали неочевидные проблемы АБ тестирования и как можно с ними справляться. Но часто бывает так, что при внедрении новой функциональности АБ тестирование провести нельзя. Например, это типично для маркетинговых кампаний нацеленных на массовую аудиторию. В данной ситуации существует вероятность того, что пользователи контрольной группы, которым недоступна рекламируемая функциональность, начнут массово перерегистрироваться. Также возможен сценарий, при котором возникнет значительное количество негативных отзывов из-за воспринимаемой дискриминации. Но задача оценки таких нововведений одна из наиболее частых, которые приходится решать аналитикам. Если метрики только улучшаются, то это обычно легко объяснить хорошей работой, а если метрика ухудшилась, то сразу появляется задача на аналитика. В этой заметке мы рассмотрим первую часть задачи -, а действительно ли метрика упала и если да, то имеет ли смысл разбираться дальше?
Первый вопрос на который нужно ответить — на какую именно метрику стоит смотреть? Предположим, что мы являемся аналитиком в компании, специализирующейся на продаже самокатов через веб-сайт. Целый месяц перед новым годом проходила массовая реклама с раздачей промо кодов со скидками на красные самокаты. Как итог — общая прибыль компании упала. Опытный аналитик сразу выявит, что на прибыль повлияли не только промокоды, но и другие факторы, такие как сезонность, внедрение нового сайта, изменение цен и несколько других влияющих факторов, которые совпали во времени с промокодами и могли оказаться не менее значимыми. Поэтому нужна более релевантная метрика, например процент пользователей воспользовавшихся промокодами и процент красных самокатов в доле проданных.
Важно определить, с чем проводить сравнение. Обычно выбирают предыдущий месяц, аналогичный календарный месяц предыдущего года или другую географическую область. Но в отсутствии хорошо спроектированного АБ теста достоверного на 100% сравнения не получится. Поэтому стоит выбирать то, что больше подходит под конкретную задачу.
Далее возникает вопрос, достаточно ли данных для применения хоть какой-то статистики? Если наблюдений всего 5–10, и они сильно зашумлены, то смысл в исследовании теряется. В этом случае чаще всего стоит остановиться с простым выводом — достоверно определить есть ли разница и почему — невозможно.
Посмотрим на типичный график, с которым приходиться работать аналитикам
Python код
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Функция генерации данных
def generate_data(n_samples: int) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=100, scale=10, size=n_samples // 2),
np.random.normal(loc=95, scale=10, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
print(test_data.head())
sns.lineplot(x="time", y="metric", data=test_data)
plt.show()
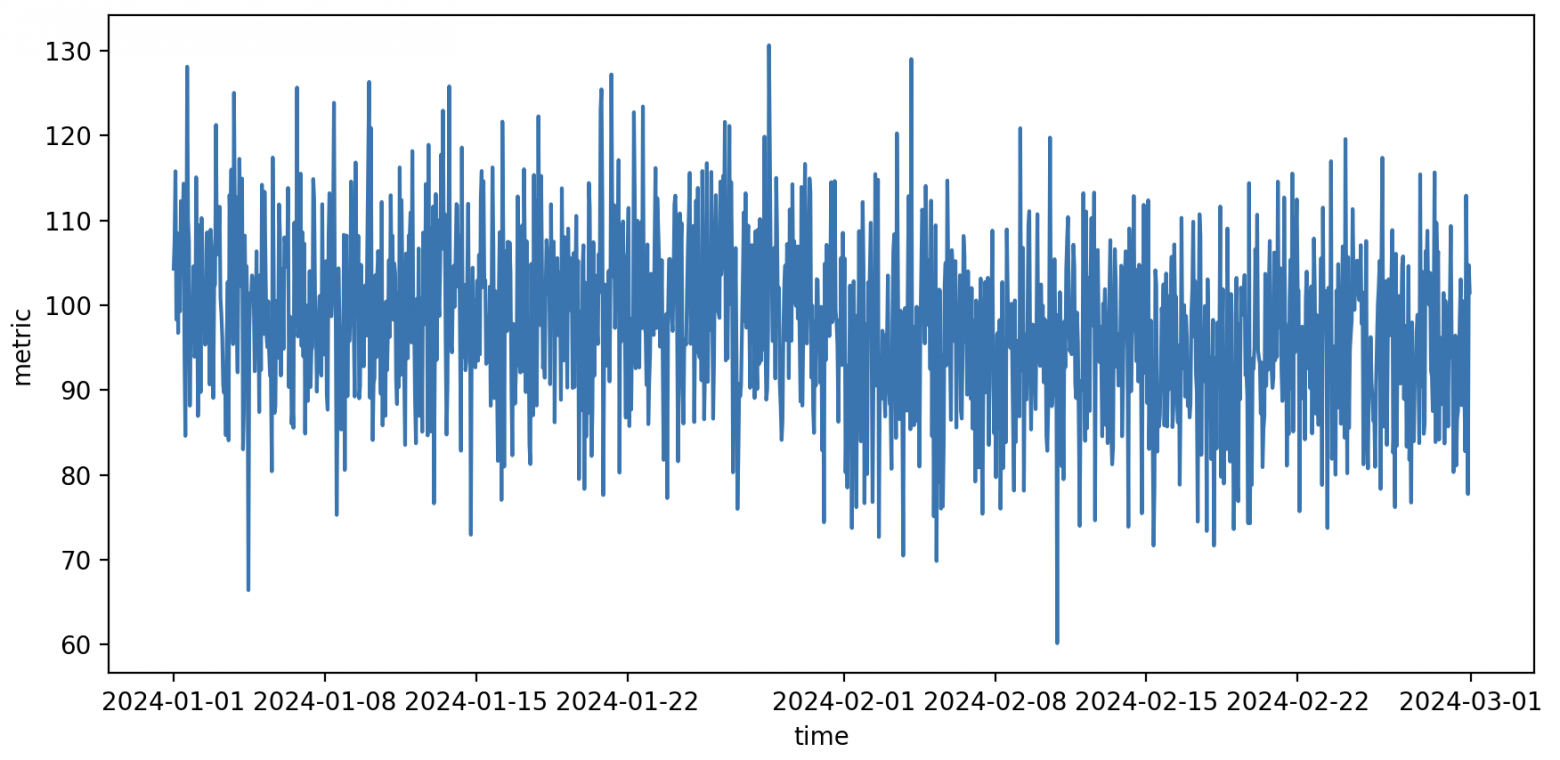
Синтетический пример шумной метрики metric за два месяца измерений.
Метрика шумная, что затрудняет визуальную оценку. При выборе двух точек данных до и после изменений можно наблюдать как увеличение, так и уменьшение значений, в зависимости от конкретных выбранных точек. Тем не менее, общее впечатление состоит в том, что среднее значение стало ниже. Как это проверить?
Простое сравнение средних
Первая идея — найти среднюю на пред периоде, среднюю на пост периоде и сравнить.
Python код
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# Функция генерации данных
def generate_data(n_samples: int) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=100, scale=10, size=n_samples // 2),
np.random.normal(loc=95, scale=10, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
print(test_data.head())
# Вычислим среднее на предпериоде и постпериоде
avg_1m = test_data.iloc[:ONE_MONTH].metric.mean()
avg_2m = test_data.iloc[ONE_MONTH:].metric.mean()
sns.lineplot(x="time", y="metric", data=test_data)
# Горизонтальной линией обозначим среднее значение метрики в первом и втором месяце
plt.hlines(
y=avg_1m,
xmin=test_data.iloc[0].time,
xmax=test_data.iloc[ONE_MONTH - 1].time,
color="red",
)
plt.hlines(
y=avg_2m,
xmin=test_data.iloc[ONE_MONTH].time,
xmax=test_data.iloc[-1].time,
color="red",
)
plt.show()
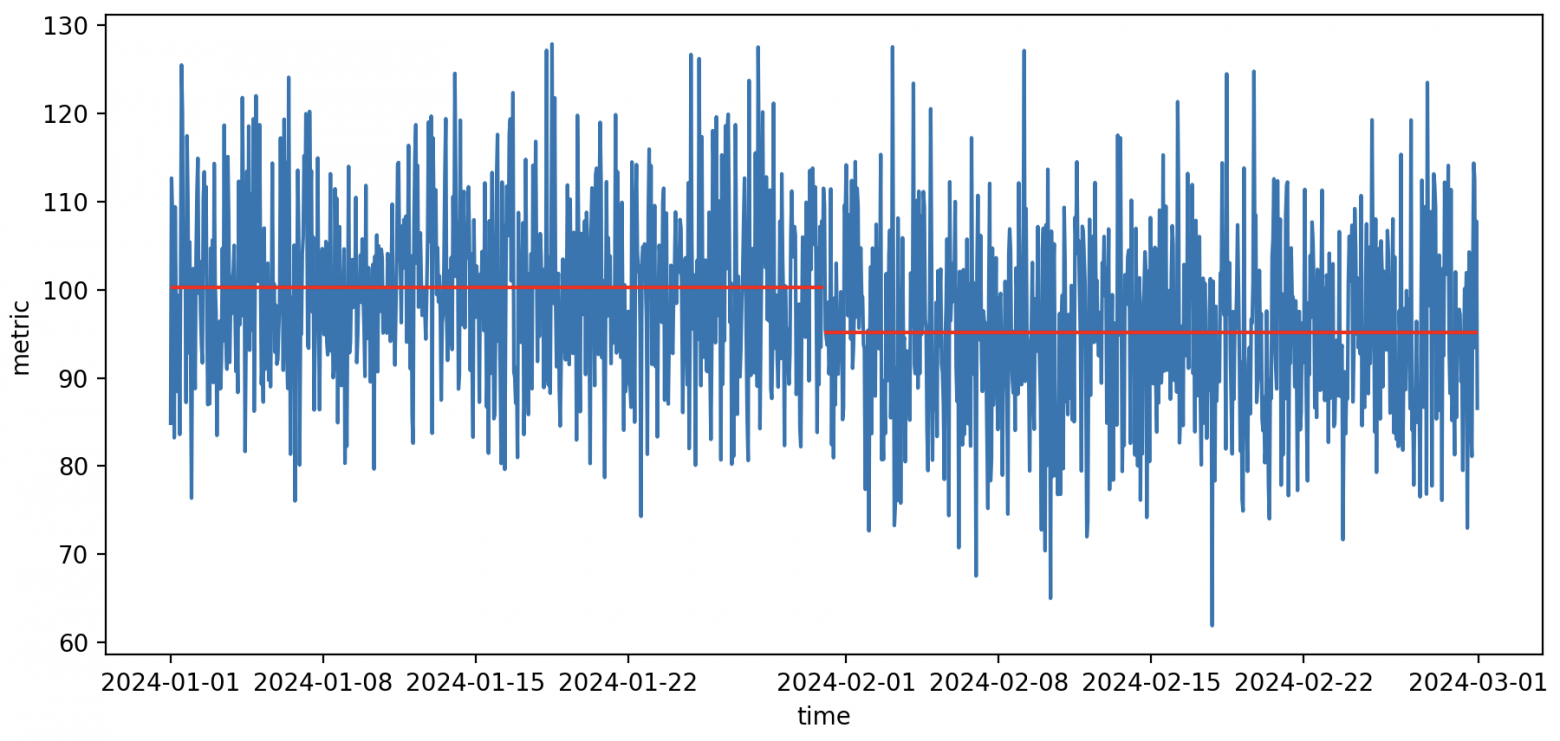
Сравнение метрики для двух соседних месяцев через сравнение средних
Даже при отсутствии реальной разницы между средними значениями, вероятность того, что два средних совпадут практически нулевая. В половине случаев правая средняя будет меньше, просто из-за случайных колебаний. Рассмотрим несколько возможных подходов для более объективного анализа.
Тест Стьюдента
t-тест, является одним из наиболее широко используемых и эффективных методов для сравнения средних значений. При его применении важно проверять условия, при которых ему можно доверять:
нормальность распределения средних
соответствие распределения ошибок хи-квадрат-распределению,
независимость случайных величин
иметь достаточно большой размер выборки для обеспечения статистической мощности теста.
Проверить можно визуально, с помощью, например, QQ-plot, либо с помощью тестов на распределение (Шапиро-Вилка, Колмогорова-Смирнова, и других). Если одно из условий нарушено, то нужно применять другие методы
Python код
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats
import seaborn as sns
# Функция генерации данных
def generate_data(
n_samples: int, loc1: int = 100, scale1: int = 10, loc2: int = 99, scale2: int = 10
) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=loc1, scale=scale1, size=n_samples // 2),
np.random.normal(loc=loc2, scale=scale2, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
data_month1 = test_data.iloc[:ONE_MONTH].metric
data_month2 = test_data.iloc[ONE_MONTH:].metric
# Проведем тест на нормальность распределения средних для первого и второго месяца
# Функция получения средних для сэмплированных подвыборок
def sample_means(data, n_samples=100, n_iterations=1000):
means = np.zeros(n_iterations)
for i in range(n_iterations):
sample = np.random.choice(data, size=n_samples, replace=True)
means[i] = sample.mean()
return means
month_1_means = sample_means(data_month1)
month_2_means = sample_means(data_month2)
if stats.shapiro(month_1_means).pvalue < 0.05:
print("Month 1 means are not normally distributed. Can't use t-test")
if stats.shapiro(month_2_means).pvalue < 0.05:
print("Month 2 means are not normally distributed. Can't use t-test")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# QQ-график для средних в первом месяце
stats.probplot(month_1_means, dist="norm", plot=ax1)
# тест на распределение chi2 средних значений за 1-й и 2-й месяцы
def sample_variances(data, n_iterations=1000):
variances = np.zeros(n_iterations)
for i in range(n_iterations):
sample = np.random.choice(data, size=len(data), replace=True)
variances[i] = sample.var()
return variances
# график распределения выборочной диспресии за месяц 1 по оси ax2
month1_variances = sample_variances(data_month1)
n1 = len(data_month1)
sns.histplot(
month1_variances * (n1 - 1) / data_month1.var(),
stat="density",
label="sample variance",
ax=ax2,
)
# построить график плотности распределения chi2 с n1-1 степенями свободы на ax2
x = np.linspace(500, 1000, 1000)
ax2.plot(x, stats.chi2.pdf(x, n1 - 1), color="red", linewidth=2, alpha=0.5)
ax2.set_xlabel("Sample variance")
ax2.set_ylabel("Density")
plt.show()
print(f"p-value: {stats.ttest_ind(month_1_means, month_2_means).pvalue:.3f}")
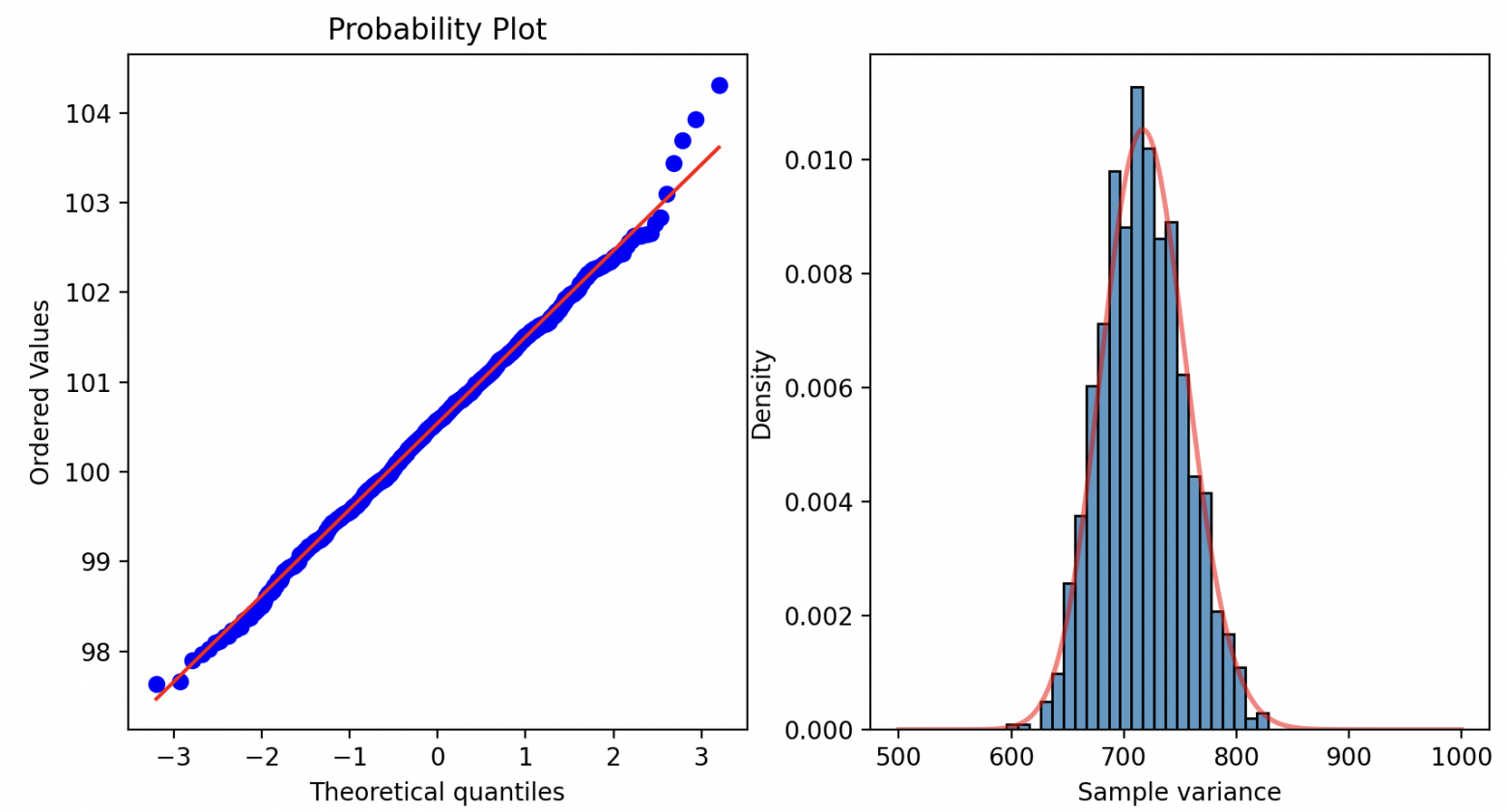
Визуальная проверка условий t-test
В рассмотренном случае различия статистически значимы.
Тест Манна-Уитни
Мана-Уитни, U-test. Этот тест не подходит для сравнения средних. Подробнее можно посмотреть в статье Ниже приведём пример моделирования 1000 тестов двух распределений с одинаковым средним и разными дисперсиями.
Python код
import numpy as np
import pandas as pd
import scipy.stats as stats
# Функция генерации данных
def generate_data(
n_samples: int, loc1: int = 100, scale1: int = 10, loc2: int = 99, scale2: int = 10
) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=loc1, scale=scale1, size=n_samples // 2),
np.random.normal(loc=loc2, scale=scale2, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
ONE_MONTH = 24 * 30
log_false_positives_t = []
log_false_positives_u = []
for _ in range(1000):
test_data = generate_data(ONE_MONTH * 2, loc1=100, loc2=100, scale1=10, scale2=100)
data_month1 = test_data.iloc[:ONE_MONTH].metric
data_month2 = test_data.iloc[ONE_MONTH:].metric
u_test_results = stats.mannwhitneyu(data_month1, data_month2)
t_test_results = stats.ttest_ind(data_month1, data_month2)
log_false_positives_t.append(t_test_results.pvalue < 0.05)
log_false_positives_u.append(u_test_results.pvalue < 0.05)
print(f"False positives for t-test: {np.mean(log_false_positives_t):.3f}")
print(f"False positives for U-test: {np.mean(log_false_positives_u):.3f}")
U-test систематически выдаёт большее количество ложных срабатываний (существенно больше чем в 5% случаев) чем t-test при одинаковом уровне alpha = 0.05. По похожим причинам не подходят тест Колмогорова-Смирнова и некоторые другие тесты, сравнивающие распределения случайных величин, вместо средних.
Бутстрап
Основная идея — генерировать 1000 новых датасетов из исходного случайным сэмплированием с повторениями и определить доверительный интервал через квантили. Применимость бутстрапа очень широка, это связано с тем, что он не требует нормальности распределения средних случайной величины. Бутстрап позволяет построить как доверительные интервалы для пост периода и предпериода в отдельности, так и интервал для разности средних. Если доверительный интервал разности средних не содержит 0, то разница статистически значима. Хорошее описание приведено в книге [Efron B. Bootstrap confidence intervals for a class of parametric problems //Biometrika. — 1985. — Т. 72. — №. 1. — С. 45–58.] https://www.jstor.org/stable/2336334
Когда выборка содержит выбросы или неточности, бутстрап может обеспечить устойчивость при оценке параметров модели, так как этот метод создает множество подвыборок, в каждой из которых могут быть учтены различные комбинации данных, включая выбросы. Анализ статистик, полученных из этих подвыборок, может предоставить информацию о диапазонах возможных значений параметров и их доверительных интервалах.
Однако стоит отметить, что бутстрап не гарантирует полное устранение влияния выбросов или грязи в данных, а также плохо работает на маленьких выборках. В некоторых случаях выбросы могут сохраняться в различных подвыборках, и они могут по-прежнему влиять на оценки модели. Бутстрап предоставляет инструмент для более устойчивой оценки, но не является универсальным средством решения всех проблем с выбросами или неточностями в данных.
Что же касается независимости наблюдений, то стоит отметить, что бутстрап создает новые подвыборки путем случайного выбора элементов из исходной выборки с возвращением, что означает, что одно и то же наблюдение может попасть в несколько подвыборок, а другие могут вовсе не войти. Это может привести к тому, что некоторые наблюдения будут дублироваться в подвыборках, в то время как другие могут быть исключены. Таким образом, бутстрап сохраняет структуру зависимости и независимости, характерную для исходных данных.
Тем не менее, важно, что если исходные данные содержат систематическую зависимость или нарушение независимости (например, временные зависимости), бутстрап может не учитывать этот аспект. В таких случаях более тщательные методы, специфичные для типа данных, могут потребоваться для учета зависимости между наблюдениями.
Python код
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Функция для генерации данных
def generate_data(
n_samples: int, loc1: int = 100, scale1: int = 10, loc2: int = 95, scale2: int = 10
) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=loc1, scale=scale1, size=n_samples // 2),
np.random.normal(loc=loc2, scale=scale2, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
# Генерируем тестовые данные
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
# Функция для выполнения бутстрапа и визуализации результатов
def bootstrap_and_plot(data, num_samples=1000, alpha=0.05):
sample_means_post = []
sample_means_pre = []
sample_diff_means = []
for _ in range(num_samples):
bootstrap_sample = data.sample(frac=1, replace=True)
# Разбиваем выборку на постпериод и предпериод
post_period = bootstrap_sample[bootstrap_sample["time"] >= "2024-02-01"][
"metric"
]
pre_period = bootstrap_sample[bootstrap_sample["time"] < "2024-02-01"]["metric"]
# Рассчитываем средние значения для постпериода и предпериода
sample_mean_post = post_period.mean()
sample_mean_pre = pre_period.mean()
sample_means_post.append(sample_mean_post)
sample_means_pre.append(sample_mean_pre)
# Рассчитываем разницу средних
sample_diff_means.append(sample_mean_post - sample_mean_pre)
# Рассчитываем доверительные интервалы для постпериода, предпериода и разницы средних
lower_bound_post = np.percentile(sample_means_post, (alpha / 2) * 100)
upper_bound_post = np.percentile(sample_means_post, (1 - alpha / 2) * 100)
lower_bound_pre = np.percentile(sample_means_pre, (alpha / 2) * 100)
upper_bound_pre = np.percentile(sample_means_pre, (1 - alpha / 2) * 100)
lower_bound_diff = np.percentile(sample_diff_means, (alpha / 2) * 100)
upper_bound_diff = np.percentile(sample_diff_means, (1 - alpha / 2) * 100)
# Визуализация результатов
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
plt.hist(sample_means_post, bins=30, edgecolor="black", alpha=0.7)
plt.axvline(
lower_bound_post,
color="red",
linestyle="dashed",
linewidth=2,
label=f"Lower Bound ({alpha * 100}% CI)",
)
plt.axvline(
upper_bound_post,
color="green",
linestyle="dashed",
linewidth=2,
label=f"Upper Bound ({(1 - alpha) * 100}% CI)",
)
plt.xlabel("Post-Period Bootstrap Sample Means")
plt.ylabel("Frequency")
plt.legend()
plt.title("Post-Period Bootstrap Sampling Distribution")
plt.subplot(1, 3, 2)
plt.hist(sample_means_pre, bins=30, edgecolor="black", alpha=0.7)
plt.axvline(
lower_bound_pre,
color="red",
linestyle="dashed",
linewidth=2,
label=f"Lower Bound ({alpha * 100}% CI)",
)
plt.axvline(
upper_bound_pre,
color="green",
linestyle="dashed",
linewidth=2,
label=f"Upper Bound ({(1 - alpha) * 100}% CI)",
)
plt.xlabel("Pre-Period Bootstrap Sample Means")
plt.ylabel("Frequency")
plt.legend()
plt.title("Pre-Period Bootstrap Sampling Distribution")
plt.subplot(1, 3, 3)
plt.hist(sample_diff_means, bins=30, edgecolor="black", alpha=0.7)
plt.axvline(
lower_bound_diff,
color="red",
linestyle="dashed",
linewidth=2,
label=f"Lower Bound ({alpha * 100}% CI)",
)
plt.axvline(
upper_bound_diff,
color="green",
linestyle="dashed",
linewidth=2,
label=f"Upper Bound ({(1 - alpha) * 100}% CI)",
)
plt.xlabel("Difference in Bootstrap Sample Means (Post-Period - Pre-Period)")
plt.ylabel("Frequency")
plt.legend()
plt.title("Difference in Bootstrap Sampling Distribution")
plt.tight_layout()
plt.show()
return (
(lower_bound_post, upper_bound_post),
(lower_bound_pre, upper_bound_pre),
(lower_bound_diff, upper_bound_diff),
)
# Выполняем бутстрап и выводим результаты
ci_post, ci_pre, ci_diff = bootstrap_and_plot(test_data)
# Выводим результаты
print(f"Доверительный интервал для постпериода: ({ci_post[0]:.2f}, {ci_post[1]:.2f})")
print(f"Доверительный интервал для предпериода: ({ci_pre[0]:.2f}, {ci_pre[1]:.2f})")
print(
f"Доверительный интервал для разницы средних: ({ci_diff[0]:.2f}, {ci_diff[1]:.2f})"
)
# Проверяем статистическую значимость разницы средних
if ci_diff[0] > 0 or ci_diff[1] < 0:
print("Разница средних статистически значима.")
else:
print("Разница средних не является статистически значимой.")
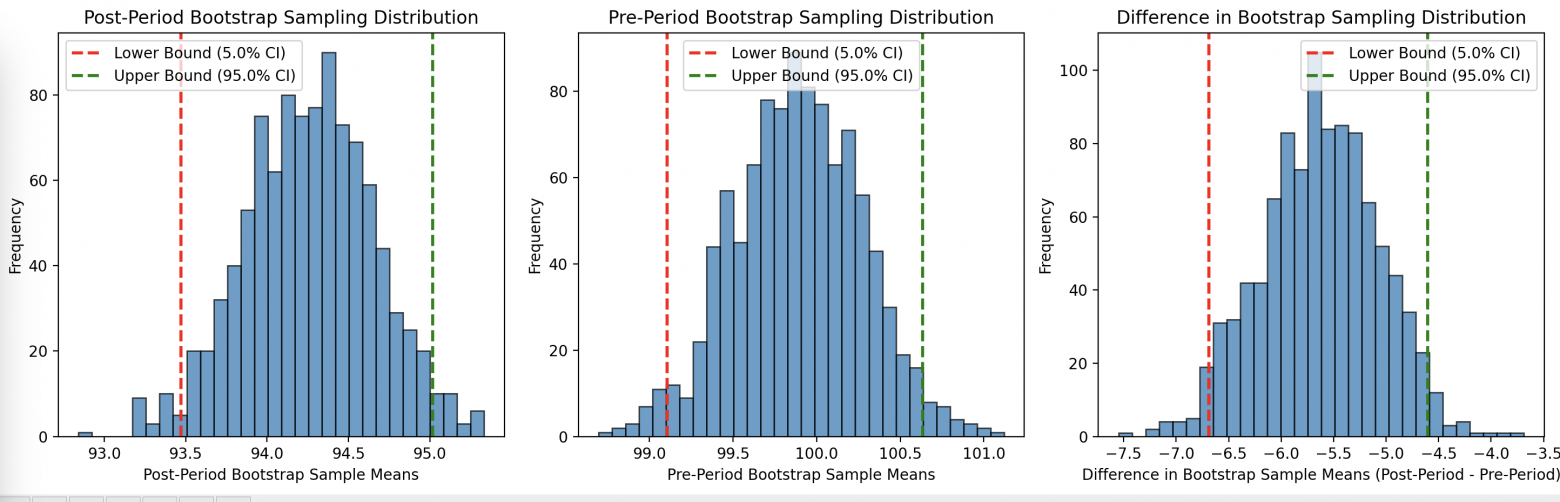
Доверительный интервал для постпериода: (94.03, 95.58)
Доверительный интервал для предпериода: (99.28, 100.73)
Доверительный интервал для разницы средних: (-6.19, -4.20). Различия статистически значимы.
Тест перестановок
В некотором смысле похож на бутстрап, но позволяет работать с выборками разного размера, хотя более вычислительно сложный. Если бутстрап на практике хорошо работает с 1000 итераций семплирования, то для теста перестановок нужно примерно 100000 итераций (подробнее описано в книге Bootstrap Methods And Permutation Tests Companion Chapter 18 To The Practice Of Business Statistics).
Тест перестановок основан на идее того, что при справедливости нулевой гипотезы распределение данных не изменится при случайных перестановках меток групп. Таким образом, сравнение наблюдаемого значения с распределением, полученным путем перестановок, позволяет делать выводы о статистической значимости различий между группами.
Python код
import numpy as np
import pandas as pd
# Функция для генерации данных
def generate_data(
n_samples: int, loc1: int = 100, scale1: int = 10, loc2: int = 95, scale2: int = 10
) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=loc1, scale=scale1, size=n_samples // 2),
np.random.normal(loc=loc2, scale=scale2, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
# Генерируем тестовые данные
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
# Разбиваем выборку на месяц 1 и месяц 2
data_month1 = test_data.iloc[:ONE_MONTH].metric
data_month2 = test_data.iloc[ONE_MONTH:].metric
# Вычисляем разницу между средними значениями
observed_diff = np.mean(data_month1) - np.mean(data_month2)
# Объединяем данные для перестановки
all_data = np.concatenate((data_month1, data_month2))
# Задаем количество перестановок
num_permutations = 100000
np.random.seed(42)
# Выполняем перестановки и считаем разницу между средними значениями для каждой перестановки
permuted_diffs = np.zeros(num_permutations)
for i in range(num_permutations):
np.random.shuffle(all_data)
permuted_diffs[i] = np.mean(all_data[:ONE_MONTH]) - np.mean(all_data[ONE_MONTH:])
# Вычисляем p-значение
p_value = np.sum(permuted_diffs >= observed_diff) / num_permutations
# Выводим результаты
print(f"P-value для перестановочного теста: {p_value:.3f}")
# Проверяем статистическую значимость
alpha = 0.05
if p_value < alpha:
print("Различие статистически значимо.")
else:
print("Различие не является статистически значимым.")
P-значение для перестановочного теста много меньше 0.05. Различие статистически значимо (alpha = 0.05).
Байесовский подход
Предположим, что метрика имеет известное распределение. Тогда можно по данным на предпериоде определить какое значение среднего является наиболее вероятным и какой у него доверительный интервал. Тоже самое можно проделать и для постпериода. Тогда сравнив два доверительных интервала можно сделать вывод о их различии. Альтернативно, можно посчитать вероятность увидеть данные постпериода, при фиксированных параметрах распределения на предпериоде. Такой подход может быть эффективным, если правильно угадать форму и тип распределения данных даже при очень не больших выборках.
Хороший пример и объяснение такого подхода можно найти на странице проекта pymc, а подробный разбор выходит далеко за рамки данной статьи. Далее в примере мы генерировали из нормального распределения, однако, на деле будет не лишним убедиться, что метрика и правда распределена нормально (или же иначе в зависимости от вашей гипотезы).
Python код
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
# Функция для генерации данных
def generate_data(
n_samples: int, loc1: int = 100, scale1: int = 10, loc2: int = 95, scale2: int = 10
) -> pd.DataFrame:
time = pd.date_range("2024-01-01", periods=n_samples, freq="1H")
data = np.concatenate(
(
np.random.normal(loc=loc1, scale=scale1, size=n_samples // 2),
np.random.normal(loc=loc2, scale=scale2, size=n_samples - n_samples // 2),
)
)
return pd.DataFrame({"time": time, "metric": data})
# Генерируем тестовые данные
ONE_MONTH = 24 * 30
test_data = generate_data(ONE_MONTH * 2)
# Разбиваем выборку на предпериод и постпериод
data_prior = test_data.iloc[:ONE_MONTH].metric.values
data_posterior = test_data.iloc[ONE_MONTH:].metric.values
# Байесовская модель для предпериода
with pm.Model() as prior_model:
mu_prior = pm.Normal("mu_prior", mu=np.mean(data_prior), sigma=np.std(data_prior))
sigma_prior = pm.HalfNormal("sigma_prior", sigma=np.std(data_prior))
likelihood_prior = pm.Normal(
"likelihood_prior", mu=mu_prior, sigma=sigma_prior, observed=data_prior
)
prior_trace = pm.sample(2000, tune=1000)
# Байесовская модель для постпериода
with pm.Model() as posterior_model:
mu_posterior = pm.Normal(
"mu_posterior", mu=np.mean(data_posterior), sigma=np.std(data_posterior)
)
sigma_posterior = pm.HalfNormal("sigma_posterior", sigma=np.std(data_posterior))
likelihood_posterior = pm.Normal(
"likelihood_posterior",
mu=mu_posterior,
sigma=sigma_posterior,
observed=data_posterior,
)
posterior_trace = pm.sample(2000, tune=1000)
plt.figure(figsize=(20, 1))
# Сравнение доверительных интервалов
prior_interval_hdi = az.hdi(prior_trace, hdi_prob=0.95)
posterior_interval_hdi = az.hdi(posterior_trace, hdi_prob=0.95)
prior_interval = [
prior_interval_hdi.sel(hdi="lower")["mu_prior"].item(),
prior_interval_hdi.sel(hdi="higher")["mu_prior"].item(),
]
posterior_interval = [
posterior_interval_hdi.sel(hdi="lower")["mu_posterior"].item(),
posterior_interval_hdi.sel(hdi="higher")["mu_posterior"].item(),
]
# Визуализация гистограммы и доверительных интервалов для mu_prior
plt.figure(figsize=(12, 6))
az.plot_posterior(prior_trace, var_names=["mu_prior"], hdi_prob=0.95)
plt.title("Prior Distribution for mu with 95% HDI")
plt.show()
# Визуализация гистограммы и доверительных интервалов для mu_posterior
plt.figure(figsize=(12, 6))
az.plot_posterior(posterior_trace, var_names=["mu_posterior"], hdi_prob=0.95)
plt.title("Posterior Distribution for mu with 95% HDI")
plt.show()
# Вывод результатов
print(f"Предпериод: ({prior_interval[0]:.2f}, {prior_interval[1]:.2f})")
print(f"Постпериод: ({posterior_interval[0]:.2f}, {posterior_interval[1]:.2f})")
if (
prior_interval[1] >= posterior_interval[0]
and prior_interval[0] <= posterior_interval[1]
):
print("Интервалы пересекаются, различие не является статистически значимым.")
# Проверка наличия пересечения интервалов
else:
print("Интервалы не пересекаются, различие статистически значимо.")
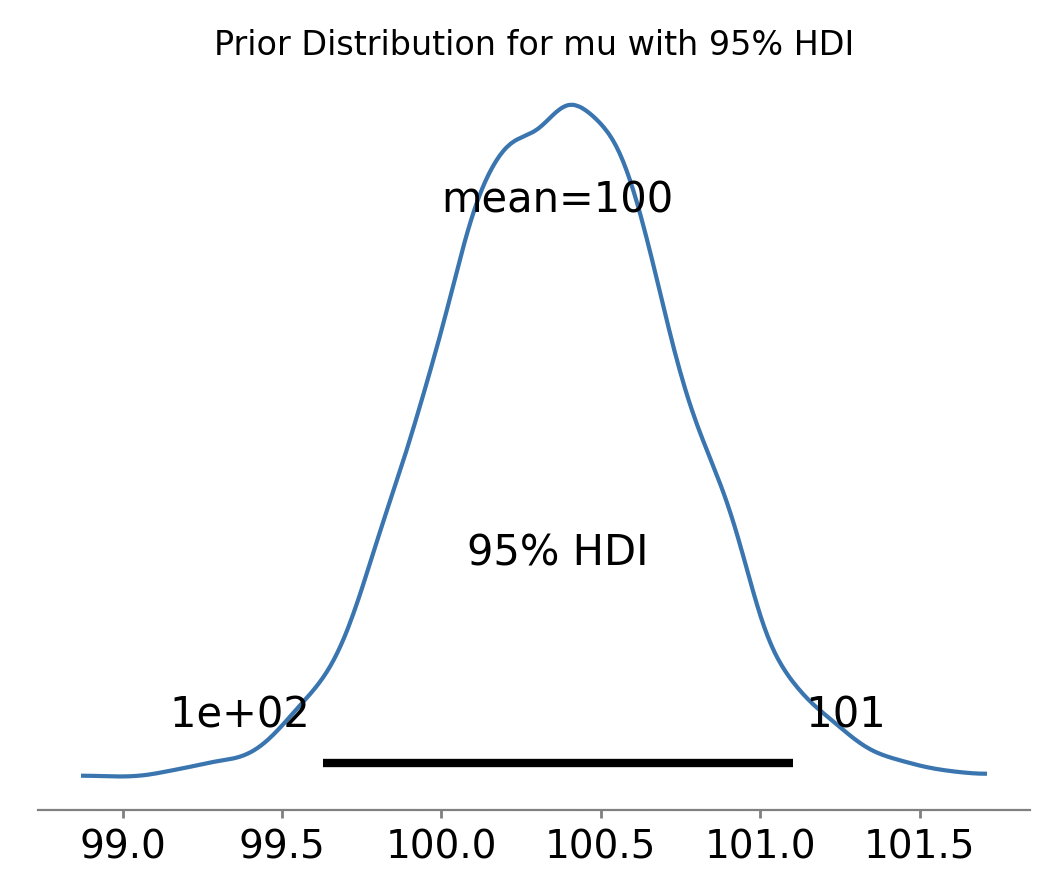
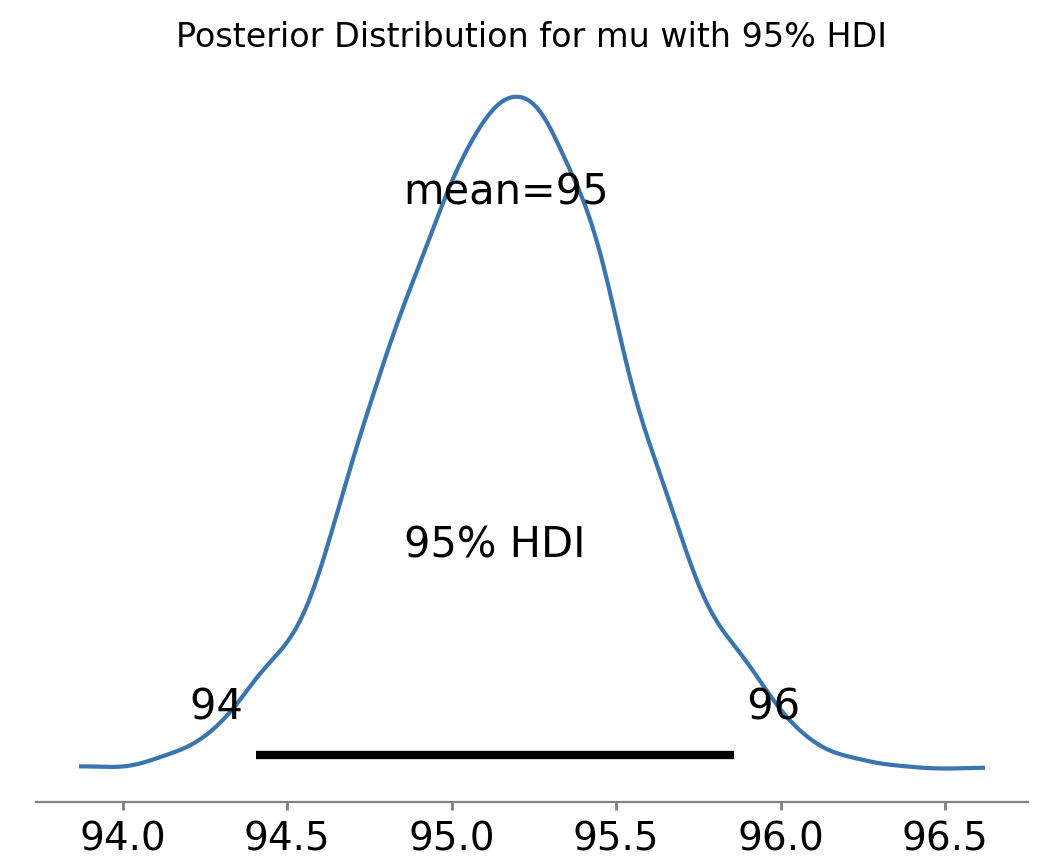
Доверительный интервал для предпериода: (99.48, 100.89)
Доверительный интервал для постпериода: (94.03, 95.50)
Интервалы не пересекаются, различие статистически значимо
Заключение
Мы рассмотрели несколько популярных подходов, но многие современные методы, связанные с машинным обучением, остались в стороне. Например подходы causal inference, Difference in Difference, и некоторые другие методы основанные на конструировании синтетического контроля можно найти например в статье Spotify, «Causal Inference in Statistics: A Primer» by Judea Pearl, «Counterfactuals and Causal Inference: Methods and Principles for Social Research» by Stephen L. Morgan and Christopher Winship, и других.
Опытный аналитик отметит, что если есть устойчивый нисходящий тренд, то при анализе стоит учитывать этот фактор, так как в таком случае на постпериоде мы всегда увидим занижение среднего. Часть указанных выше продвинутых методов позволяют учесть тренд, но для начала нужно определить, а есть ли тренд? В следующей статье мы обсудим подходы к определению тренда и их применимость на практике.
Авторы
Заремба Анастасия
Рудницкий Роман
Юлдашев Марат
