Теория временных рядов, применение трансформеров

Читая главы книг по статистическому анализу, я часто вижу анализ или прогнозирование временных рядов. В этой статье я опишу некоторые основные понятия в теории анализа временных рядов, классические статистические алгоритмы прогнозирования, а так же рассмотрю применение моделей глубоких нейросетей для таких задач .
Поэтому, если Вы готовы погрузиться в одну из интереснейших тем статистики и Вы любитель машинного обучения, продолжайте читать).
Временной ряд отличается от обычной последовательности тем, что каждое его значение взято на одинаково расположенных точках времени. На обложке статьи показан пример.
Стоит упомянуть, что мы можем найти очень большое количество литературы об алгоритмах анализа временных рядов, потому, что необходимость прогнозировать именно этот тип данных возникает задолго до машинного обучения. В промышленности многие специалисты по данным до сих пор используют простые авторегрессионные модели вместо глубокого обучения для предсказания временных рядов. Обычно основными причинами выбора этих методов остаются интерпретируемость, ограниченность данных, простота использования и стоимость обучения. Поэтому, первая часть статьи посвящена статистике: статистические понятия в анализе временных рядов и классические алгоритмы прогнозирования.
Компоненты и временного ряда и аналитические коэффициенты
Основные понятия в статистическом анализе временных рядов:
Тренд — компонента, описывающая долгосрочное изменение уровня ряда.
Сезонность — компонента, обозначаемая как Q, описывает циклические изменения уровня ряда.
Ошибка (random noise) — непрогнозируемая случайная компонента, описывает нерегулярные изменения в данных, необъяснимые другими компонентами.
Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда. Это один из самых важных коэффициентов в анализе временного ряда. Чтобы посчитать автокорреляцию, используется корреляция между временным рядом и её сдвинутой копией от величины временного сдвига. Сдвиг ряда называется лагом.
Автокорреляционная функция— график автокорреляции при разных лагах
 Компоненты ряда
Компоненты ряда
К такому графику, можно добавить также визуализацию автокорреляционной функции.
Стационарный ряд — ряд, в котором свойства не зависят от времени. При таких компонентах ряда, как тренд или сезонность, ряд не является стационарным. Это интуитивное понятие. На практике есть два вида стационарности — строгая и слабая. В следующих алгоритмах, нам достаточно слабой. Она заключается в постоянной дисперсии (без гетероскедастичности) и в постоянности среднего значения ряда.
Гетероскедастичность — не равномерная дисперсия. То есть, не однородность наблюдений.
В python, например, реализованы библиотеки, через которые мы можем проверить ряд на стационарность, гетероскедастичность или построить автокорреляционную функцию.
Статистические модели предсказания
Перейдём к самому интересному — прогнозирование.
Авторегрессионная модель (Auto regression method (AR))
Это линейная модель, в которой прогнозированная величина является суммой прошлых значений, умноженных на числовой множитель.
Скользящее среднее (Moving average method (MA))
Скользящее среднее-это расчет для анализа точек данных путем создания ряда средних значений различных подмножеств полного набора данных. Мне этот метод часто напоминает Тренд ряда. Скользящее среднее часто применяется для анализа временных рядов акций.

Метод скользящего среднего с авторегрессией и интегрированием (Auto regressive integrated moving average (ARIMA)
Существует также модель ARMA. Которая представляет собой сочетание моделей выше. Разница между моделями ARMA и ARIMA описана ниже.
Теорема Волда — утверждение математической статистики, согласно которому каждый временной ряд можно представить в виде скользящего среднего бесконечного порядка
Так как модель ARMA , согласно теореме о разложении Волда , теоретически достаточна для описания регулярного стационарного временного ряда, мы заинтересованы в стационарности ряда.
Почему стационарность так важна? Предполагается, что, если временной ряд ведет себя определенным образом, очень высока вероятность того, что он повторит те же паттерны в будущем.
Поэтому, нам стоит применить преобразование для нестационарного ряда. Здесь есть два подхода — удаление тренда и взятие разности. Почему тут интегрирование? В математике есть раздел — исчисление конечных разностей, в котором интегрированием называется взятие разности.
Вот такое скромное описание основных моделей прогнозирования, применяемых ещё до машинного обучения. Если вам интересна эта тема, советую почитать об ARIMA с сезонностью (Seasonal auto regressive integrated moving average (SARIMA)) или о моделях ARCH, GARCH
Нейронные сети для предсказания временных рядов
Давайте рассмотрим, с какими проблемами может столкнуться нейронный алгоритм в работе с временными рядами.
Далее, для понимания я буду напоминать основы моделей.
Первое, что приходит на ум — это, конечно, рекуррентные нейросети.
Одна из идей, сделавшая RNN неоправданно эффективными — «авторегрессия» (auto-regression), это значит, что созданная переменная добавляется в последовательность в качестве входных данных. В машинном обучении часто применяется эта техника, особенно в работе с временными рядами.
Хотя рекуррентная сеть и должна работать со всей последовательностью, к сожалению, присутствует проблема «затухающего градиента»(vanishing gradient problem). Что значит, что более старые входы не влияют на текущий выход. Такие модели, как LSTM пытаются решить эту проблему, добавляя дополнительные параметры (separate memory).

Такие модели считывают ввод данных последовательно. Если Вам интересна это тема, советую узнать также об алгоритме Seq2Seq. Нам нужна архитектура, в которой обработка последовательности производится сразу, что практически не оставляло бы места для потери информации. Да, такая архитектура реализована в кодировщике модели Transformer. Эта характеристика позволяет модели изучать контекст переменной на основе всего его окружения. Кроме того, по сравнению с рекуррентными нейросетями, чаще всего они быстрее.
Алгоритм внимания и Transformer для временных рядов
Эта относительно новая идея слоя внимания очень интересна. Чаще всего такие модели применяются для обработки последовательностей текста. В этой статье я опишу некоторое количество разновидностей моделей со слоем внимания, но углубляться в модели, используемые только для текста (BERT, GPT-2 и XLNet), конечно, я не буду. Хотя, с их недавним успехом в НЛП можно было бы ожидать широкой адаптации к прогнозированию временных рядов.
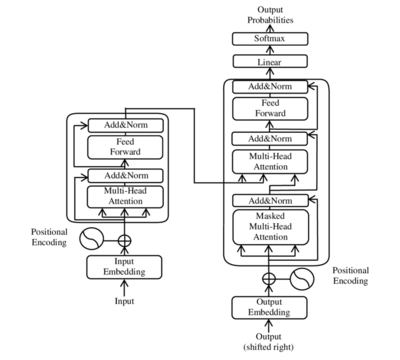
Оригинальная архитектура трансформера (Vanilla Transformer) является авто-энкодером. Кодер получает на вход последовательность с позиционной информацией. Декодер получает на вход часть этой последовательности и выход кодировщика. Но архитектура некоторых моделей на основе трансформера состоит только из encoder. Например, BERT.
Как можно заметить, модель состоит из преобразования входных векторов, позиционного кодирования, нормализации, слоёв прямого распространения, линейного слоя и слоёв внимания.
В психологии внимание — это концентрация сознания на одних стимулах, исключая другие. Слой внимания в нейросетях — математические модели, позволяющие оценить взаимосвязь между значениями. Возможно я не одна заметила интуитивное сходство с автокорреляцией

Вот пример визуализации результата простого слоя внимания для последовательности слов. Таким образом, трансформеры сохраняют прямые связи со всеми предыдущими временными значениями, позволяя информации распространяться по гораздо более длинным последовательностям. Весь механизм помещён в формулу с функцией softmax
Более подробное описание слоя внимания
Давайте рассмотрим слой внимания в трансформерах поближе. Для примера возьмём последовательность слов. Далее мы рассмотрим применение таких архитектур и для временных рядов.
Из того, что все элементы последовательности подаются сразу следует, что нам нужно добавить некоторую информацию, указывающую порядок элементов. Для этого мы вводим технику, называемую позиционным кодированием (pos.encoding). Здесь применяется функция синуса или косинуса. На изображении архитектуры сети её можно заметить.
Обратите внимание на архитектуру трансформера выше. Можно заметить, что слой внимания принимает три значения. Это преобразованные входные вектора. Итак, для каждого слова мы создаем вектор запроса, вектор ключа и вектор значения (Query vector, a Key vector, and a Value vector ). Эти вектора создаются путем умножения вложения на три матрицы весов.
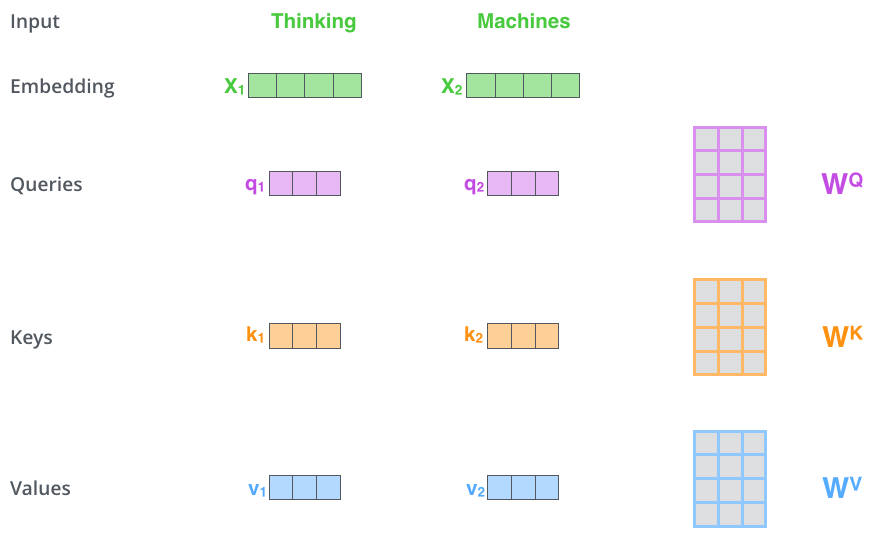
Далее рассчитывается оценка путём скалярного умножения вектора ключа на вектор запроса.
Нам нужно сопоставить каждое слово входного предложения с этим словом. Оценка определяет, сколько внимания нужно уделять другим частям входного предложения, когда мы кодируем слово в определенной позиции.
В целях нормализации, стоит разделить полученное значение на квадратный корень из размерности векторов ключа.
Полученное значение помещаем в функцию softmax. Softmax нормализует оценки, чтобы все они были положительными и в сумме давали 1 .
Такой вот коэффициент мы получили. Теперь, с помощью умножения на значение (V) можно получить обработанный вектор
Для вывода слоя (получения результирующего вектора) остаётся произвести суммирование

Результирующий вектор — это тот, который мы можем отправить в нейронную сеть с прямой связью.
Я попыталась интуитивно описать следующую формулу
 Виды трансформеров и их результаты в задаче прогнозирования временных рядов электричества
Виды трансформеров и их результаты в задаче прогнозирования временных рядов электричества
Существуют работы, посвященные моделям для прогнозирования временных рядов на основе трансформера. Давайте рассмотрим некоторые из них.
Первая работа, которая мне очень понравилась — Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. Здесь на примере задачи прогнозирования гриппоподобных заболеваний автор сопоставил некоторые результаты различных моделей, работающих с временными рядами.
Архитектура очень похожа на оригинальный трансформер. В качестве оптимизатора в этой работе использовался Adam. Для регуляризации авторы добавили dropout и dropout rate — 0.2 для каждого слоя.
Посмотрим на результаты модели, оценка которой взята с RMSE и с коэффициентом корреляции
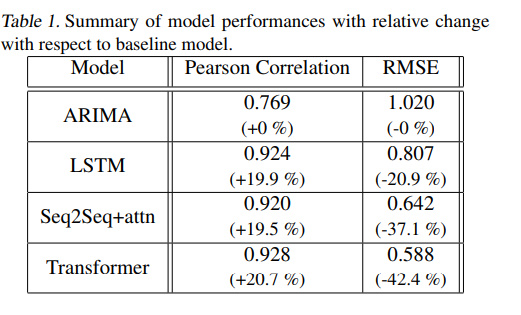
В следующей работе — Adversarial Sparse Transformer for Time Series Forecasting, нужно быть знакомым с генеративно-состязательными нейросетями, потому, что автор применил очень интересную идею создания генеративной модели для прогнозирования.

Применяется стохастический градиентный спуск
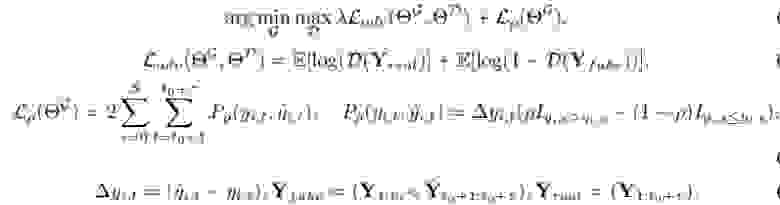 Оптимизация
Оптимизация
где: ΘG — параметры генератора , ΘD — параметры дискриминатора.
Обучилась нейросеть на данных часового ряда потребления электроэнергии (electricity).
В результате, ошибка обычного трансформера примерно в 3 раза меньше, чем ARIMA (0.036), а ошибка модели описанной выше в 4 раза меньше, чем ARIMA (0.025)
Вообще, большее количество типов данных сейчас предсказывается с использованием глубоких нейросетей. Некоторые архитектуры позволяют это сделать и для временных рядов.
Использованная литература:
https://docs.yandex.ru/docs/view? tm=1665624573&tld=ru&lang=en&name=504_05_Box_Time-Series-Analysis-Forecasting-and-Control-2015.pdf&text=time series book&url=http%3A%2F%2Fwww.ru.ac.bd%2Fstat%2Fwp-content%2Fuploads%2Fsites%2F25%2F2019%2F03%2F504_05_Box_Time-Series-Analysis-Forecasting-and-Control-2015.pdf&lr=103616&mime=pdf&l10n=ru&sign=377cc2ae7c1308edb3a8377df8accb49&keyno=0&nosw=1&serpParams=tm%3D1665624573%26tld%3Dru%26lang%3Den%26name%3D504_05_Box_Time-Series-Analysis-Forecasting-and-Control-2015.pdf%26text%3Dtime%2Bseries%2Bbook%26url%3Dhttp%253A%2F%2Fwww.ru.ac.bd%2Fstat%2Fwp-content%2Fuploads%2Fsites%2F25%2F2019%2F03%2F504_05_Box_Time-Series-Analysis-Forecasting-and-Control-2015.pdf%26lr%3D103616%26mime%3Dpdf%26l10n%3Dru%26sign%3D377cc2ae7c1308edb3a8377df8accb49%26keyno%3D0%26nosw%3D1
https://en.wikipedia.org/wiki/Time_series
https://docs.yandex.ru/docs/view? tm=1665625434&tld=ru&lang=en&name=Business Intelligence — Carlo Vercellis.pdf&text=Business Intelligence Carlo Vercellis&url=http%3A%2F%2Fwww.biomedicahelp.altervista.org%2FMagistrale%2FClinics%2FBIC_PrimoAnno%2FIdentificazioneModelliDataMining%2FBusiness%2520Intelligence%2520-%2520Carlo%2520Vercellis.pdf&lr=103616&mime=pdf&l10n=ru&sign=d5d4bbb9a8488b541cb4f47462763a53&keyno=0&nosw=1&serpParams=tm%3D1665625434%26tld%3Dru%26lang%3Den%26name%3DBusiness%2520Intelligence%2520-%2520Carlo%2520Vercellis.pdf%26text%3DBusiness%2BIntelligence%2BCarlo%2BVercellis%26url%3Dhttp%253A%2F%2Fwww.biomedicahelp.altervista.org%2FMagistrale%2FClinics%2FBIC_PrimoAnno%2FIdentificazioneModelliDataMining%2FBusiness%252520Intelligence%252520-%252520Carlo%252520Vercellis.pdf%26lr%3D103616%26mime%3Dpdf%26l10n%3Dru%26sign%3Dd5d4bbb9a8488b541cb4f47462763a53%26keyno%3D0%26nosw%3D1
https://www.youtube.com/watch? v=u433nrxdf5k&t=1105s
https://medium.com/analytics-vidhya/time-series-forecasting-a-complete-guide-d963142da33f
https://arxiv.org/abs/1810.04805
https://towardsdatascience.com/attention-for-time-series-classification-and-forecasting-261723e0006d
https://srome.github.io/Understanding-Attention-in-Neural-Networks-Mathematically/
https://arxiv.org/pdf/1706.03762.pdf
https://ru.wikipedia.org/wiki/Теорема_Волда
https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average
http://jalammar.github.io/illustrated-transformer/
https://arxiv.org/pdf/2001.08317.pdf
Adversarial Sparse Transformer for Time Series Forecasting, by Sifan Wu et al.
Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case, by Neo Wu, Bradley Green, Xue Ben, & Shawn O’Banion
https://www.youtube.com/watch? v=HEh4–2J77Hg
https://arxiv.org/pdf/2006.07214.pdf
