Теория счастья. Закон арбузной корки и нормальность ненормальности10.07.2018 08:33

Представляю на суд читателей Хабра неупорядоченные главы из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

В этой главе мы начнём с анализа арбузов и их корок, выясним их связь со знаменитым законом Мерфи и убедимся со всей строгостью в том, что о вкусах не спорят.

Мне одному кажется, что я нормальный?

Как часто, глядя новости, или читая комментарии к ним, мы недоумеваем: «Есть в этом мире нормальные люди?!» Вроде как, должны быть, ведь нас много, и в среднем, мы и должны быть нормальны. Но при этом мудрецы говорят, что каждый из нас уникален. А подростки уверены, что они-то уж точно отличаются от серой массы «нормальных людей» и ни на кого не похожи.

Читатели, знакомые со статистикой, конечно же, много раз видели как для различных несимметричных распределений мода (максимум на графике плотности вероятности) не совпадает со средним значением или математическим ожиданием. То есть, среднее значение не соответствует самой большой плотности вероятности, но всё равно, на то оно и ожидаемое, чтобы быть если уже и не самым часто встречающимся, то, по крайней мере, доминирующим. Однако, не всё так просто. До сих пор мы рассматривали одновариантные распределения — распределения в одномерном пространстве исходов. Но жизнь многогранна, и уж точно не одномерна! А при добавлении дополнительных размерностей могут случаться весьма неожиданные вещи.

Одна из особенностей многомерной геометрии — увеличение доли пограничных значений в ограниченном объёме. Вот что имеется в виду. Рассмотрим классическую задачу об арбузе в пространствах с различной размерностью и зададимся целью выяснить, сколько же чудесной сахарной мякоти нам достанется от этого огромного, крепкого и аппетитного арбуза, если надрезав его, мы выяснили, что толщина его корки не превышает $15\%$ от его радиуса? Кажется, что $15\%$ это уж больно много, но посмотрите на рисунок вначале статьи, пожалуй, арбуз с такими пропорциями мы сочтём вполне приемлемым.

Начнём с одномерного арбуза — это розовый столбик, а его корка представляет собой два маленьких белых отрезочка по краям. Суммарная длина корки — это аналог объёма в одномерном мире — составит $15\%$ от общей длины арбуза. У двумерного, блинообразного арбуза, корка в виде белого кольца, по площади будет меньше, чем его внутренняя часть, уже всего в три раза. В привычном нам трёхмерном мире, такая корка составит почти $40\%$ общего объёма. Чувствуется подвох.

Доли, которые занимает корка в арбузе различной размерности.

Для шара, как, впрочем, и для тела произвольной формы, можно получить зависимость отношения объёма корки к общему объёму тела. Она выражается через отношение толщины корки к характерному размеру тела $d$ и является показательной функцией размерности пространства $m$ :

$\frac{V_{корки}}{V_{общ}} = 1 - \left(1 - d\right)^m.$

Вот как выглядит график роста доли пятнадцатипроцентной по радиусу корочки арбуза в его объёме, при дальнейшем увеличении размерности пространства.

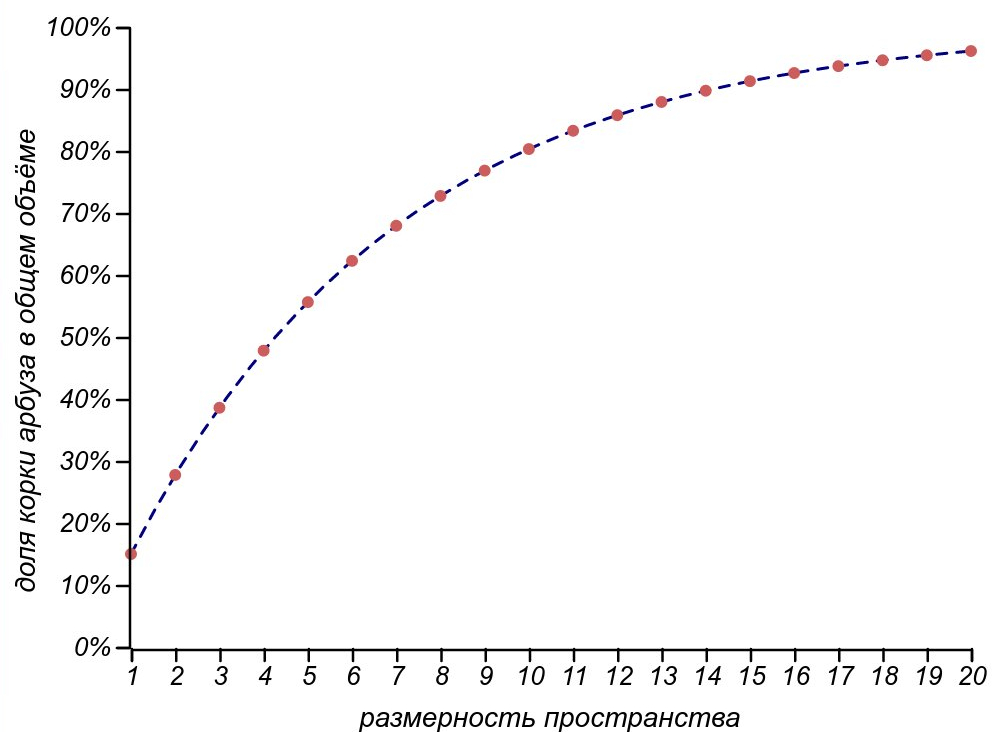
В четырёхмерном пространстве наш условно тонкокорый арбуз оставит нам уже лишь половину мякоти, а в одиннадцатимерном мире мы сможем полакомится лишь $15\%$ от всего арбуза, выбросив корочку, составляющую $15\%$ его радиуса!

Итак, мы готовы сформулировать глубокомысленный закон арбузной корки:

Покупая многомерный арбуз, ты приобретаешь, в основном, его корку.

Обидно, конечно, но какое это имеет отношение к нормальности нашего мира и к законам подлости? Увы, именно он препятствует отысканию так называемой «золотой середины», обесценивает результаты социологических опросов и повышает роль маловероятных неприятностей.

Дело в том, что пространство людей со всеми их параметрами существенно многомерно. Вполне независимыми размерностями можно счесть и очевидные рост, вес, возраст и достаток, а также, уровни интеллектуального (IQ) и эмоционального (EQ) развития, наконец, наблюдаемые, хоть и плохо формализуемые черты лица, либо черты характера, такие как уровень болтливости, упрямства или влюбчивости. Мы без труда насчитаем с десяток-полтора параметров, характеризующих человека. И для каждого из этих параметров существует некая статистически определяемая «норма» — наиболее ожидаемое и более того, часто наблюдаемое значение. Сколько же в таком богатом пространстве параметров окажется людей, типичных во всех отношениях? Выражение, которое мы использовали для вычисления отношения объёмов корки и арбуза, можно использовать и для вычисления вероятности попасть в число хоть в чём-то, но «ненормальных» людей. Действительно, вероятность удовлетворить всем критериям типичности одновременно равна произведению вероятностей оказаться типичным по каждому критерию в отдельности.

Сейчас мы сильно упростим задачу, чтобы не писать пугающих формул, по которым нельзя ничего толком вычислить. Предположим, что качества людей по каждому из направлений подчиняются нормальному (гауссовому) распределению вокруг некоторого среднего значения. Это, конечно чрезвычайно смело, но вполне разумно для наших целей, ведь мы говорим не о каком-то конкретном наборе характеристик, а, прямо скажем, фантазируем, стараясь сформулировать хоть что-то определённое в столь зыбкой теме. Поэтому загружаться подробностями, пока не видна самая общая картина, рановато. Итак, все критерии мы подчинили нормальному распределению со своими средними и дисперсиями. Значит, мы можем определить параметры самого типичного человека на свете, и отсчитывать отклонения от них. Кроме того, нам неважно какие конкретно значения дисперсии, окажутся у каждого критерия, ведь нас интересует лишь вероятность выйти за пределы стандартного отклонения, а это значение от масштаба самого распределения не зависит. Всё это приводит к тому, что если обозначить за $P_{out}$ вероятность оказаться за пределами области, ограниченной стандартным отклонением (оказаться во внешней «корочке» распределения, похожей, скорее, не на корку арбуза, а на атмосферу Земли, уходящую далеко в космическое пространство, становясь всё тоньше и тоньше), то вероятность оказаться в чём-то ненормальным, при рассмотрении $m$ критериев, будет вычисляться по «арбузной» формуле:

$P = 1 - \left(1 - P_{out}\right)^m.$

Для гауссового распределения $P_{out}=1 - CDF(\sigma) + CDF(-\sigma) = 32\%$ , где $\sigma$ — стандартное отклонение.

Вероятности оказаться «ненормальным» для различного числа критериев сравнения и для различной «строгости» определения нормы. Верхний и нижний графики отличаются тем, что при определении «нормальности» используют радиус в одно и два стандартных отклонения, соответственно.

Что же, выходит, это нормально — быть хоть в чём-то ненормальным. Оценивая людей по десятку параметров, будьте готовы к тому, что полностью заурядными окажутся лишь 2% общей популяции. Причём, как только мы их разыщем, они тут же станут знаменитостями, потеряв свою заурядность!

Тот самый закон подлости

Один из классических законов подлости, сформулированный в сердцах инженером Эдвардом Мёрфи, гласит:

«Всё, что может пойти не так, пойдет не так».

Он несколько глубже, чем тривиальное утверждение о том, что в полной выборке наблюдаются все исходы, даже самые маловероятные.

Пусть для выполнения некоторой работы требуется совершить ряд действий, и для каждого из них существует маленькая вероятность неудачи. Какова вероятность того, что всё пройдёт без сучка без задоринки? Всё просто — нужно перемножить вероятности успеха для всех шагов. И тут же включается закон арбузной корки: чем больше число шагов, тем существеннее роль границ, в нашем случае, внештатных ситуаций. Достаточно дюжины шагов, чтобы 5% вероятности ошибки на каждом из них, выросли до 50% вероятности провала всего дела! То же самое относится и к сложным системам со множеством частей, каждая из которых может отказать. В простейшем случае, вероятность отказа системы вычисляется из вероятности отказа каждой её части по тому же самому закону арбузной корки.

Эти наши рассуждения чрезвычайно просты, а закон Мерфи скорее эмоционален, чем объективен и кажется трюизмом, но всё же, именно с этого наблюдения в сороковые-пятидесятые годы двадцатого века началась новая большая наука: теория надёжности. Она добавила в рассмотрение время, взаимосвязь элементов систем, экономику, а также человеческий фактор и нашла применение за пределами инженерных наук: в экономике, теории управления и, наконец, в программировании.

Мы ещё вернёмся к этой теме, когда будем изучать закон последнего дня, который заставляет принтер барахлить именно в день сдачи проекта. Закон Мерфи с учётом времени — поистине страшная сила! А пока вернёмся к теме уникальности и нормальности.

Счастье — это найти друзей с тем же диагнозом, что и у тебя

Все мы разные, это понятно, а можно ли вообще ставить вопрос о соответствии какой-то норме, не пытаемся ли мы при этом оценивать и сравнивать? Вы спросите, что же в этом плохого? Мы всё время кого-нибудь с кем-нибудь сравниваем, чаще всего, себя с другими, но иногда позволяем оценить и кого-нибудь ещё. Однако, с точки зрения математики, всё не так просто.

Сравнивать — значит определять отношение порядка. То есть обозначать, что один элемент некоего множества, в каком-то смысле, предшествует другому. Этому мы научились ещё в школе: 2 меньше чем 20, слон слабее кита, договор дороже денег и т. п. Но вот вам ряд вопросов. Что идёт раньше понедельник или вторник? А воскресенье или понедельник? А какое воскресенье — то, что перед понедельником, или то, что после субботы? А какое число больше: 2+3i или 3+2i? Мы можем назвать по порядку цвета радуги и даже ассоциировать все промежуточные цвета с вещественным числом — частотой света, но кроме этих цветов существует множество неспектральных цветов, они образуют хорошо знакомый типографам и дизайнерам цветовой круг, можно ли все видимые глазом цвета выстроить по порядку? Эти примеры показывают, что с отношением порядка бывают трудности. Например, на множестве дней недели не работает транзитивность (из того, что за $A$ следует $B$ , а за $B$ следует $C$ не следует, что $C$ всегда следует за $A$ ). Попытка ввести понятие больше/меньше на поле комплексных чисел не согласуется с арифметикой этих чисел, а цвета обладают обоими этими недостатками.

И как же можно сравнивать людей, книги, блюда, языки программирования и прочие объекты, имеющие множество параметров, пусть даже условно формализуемых? В принципе, можно, но только сперва договорившись об определениях и метриках, а иначе это будет бесконечный, бурный и бессмысленный спор. Увы, жаркие споры возникают чаще всего уже на этапе выбора метрик, поскольку они сами образуют некое множество, на котором тоже нужно определять отношение порядка.

Впрочем, можно предложить вполне осмысленный и однозначный способ рассуждений о сравнимости многомерных объектов, например, людей. В многомерном пространстве параметров каждый объект может быть представлен вектором — набором чисел — значений критериев, которые его характеризуют. Рассматривая ансамбль векторов (например, человеческое общество), мы увидим, что какие-то из них окажутся сонаправлены, или, по крайней мере, близки по направлениям, вот их-то уже вполне можно сравнивать по длине. В тоже время, какие-то векторы будут ортогональны (в геометрическом смысле — перпендикулярны, в более широком — независимы), и соответствующие им люди будут попросту друг другу непонятны: они по ряду параметров окажутся в сопряжённых пространствах, как пресловутые физики и лирики. Нет смысла рассуждать о том, что хороший поэт в чём-либо лучше или хуже талантливого инженера или одарённого природой спортсмена. Единственное, о чём можно судить, это о длине вектора — о степени одарённости, о расстоянии от среднего.

В этой связи может возникнуть любопытный вопрос:, а какая доля случайных векторов в пространстве заданной размерности будет сонаправленной, а какая — ортогональной? Как много удастся найти единомышленников или, хотя бы, тех с кем можно себя сравнить?

В двухмерном мире каждому вектору соответствует одномерное пространство коллинеарных (сонаправленных) и одномерное пространство ортогональных векторов. Если мы рассмотрим «почти» сонаправленные и «почти» ортогональные вектора, то они образуют секторы одинаковой площади при одинаковом выборе допустимого отклонения. То есть похожих и непохожих объектов, при рассмотрении двух критериев, будет одинаковое количество.

Почти коллинеарные и почти ортогональные векторы в двухмерном и трёхмерном пространстве.

В трёхмерном мире картина поменяется. Сонаправленные векторы всё также образуют одномерное пространство, а вот ортогональные уже заполняют плоскость — двухмерное пространство. Фиксируя длину векторов $R$ и допуская небольшое отклонение от идеальных направлений на угол $\Delta\varphi$ , можно число почти сонаправленных векторов сопоставить с площадью круговых областей вокруг полюсов $2\pi(R \Delta\varphi)^2$ , а число почти ортогональных векторов — с площадью полосы вокруг экватора: $4\pi R^2\Delta\varphi$ . Их отношение $2/ \Delta\varphi$ при уменьшении отклонения $\Delta\varphi$ растёт неограниченно.

В четырёхмерном мире ортогональные векторы образуют уже трёхмерное пространство, тогда как сонаправленные векторы всё ещё лежат в одномерном, и разница в их количестве растёт уже пропорционально квадрату отклонения от идеала. Но на этом этапе лучше обратиться к теории вероятностей и выяснить каковы шансы получить ортогональные или сонаправленные векторы, взяв наугад два вектора из пространства, размерности $m$ ? Об этом нам расскажет распределение углов между случайными векторами. К счастью, рассуждая о площадях многомерных сфер, его можно вычислить аналитически и представить в конечной форме:

$p(\varphi) = \frac{\Gamma(m/2)}{\sqrt{\pi}\,\Gamma((m-1)/2)}\sin(\varphi)^{m-2},$

Здесь $\Gamma(x)$ — это гамма-функция, обобщение факториала на вещественные (и даже комплексные) числа.

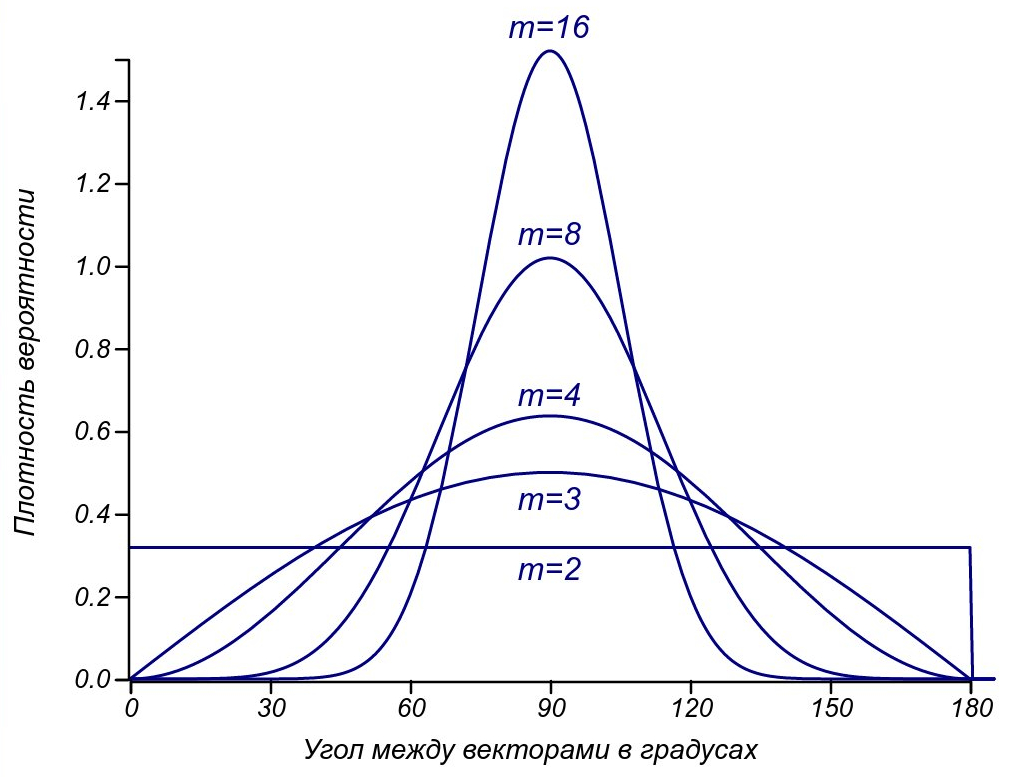
Распределения углов случайных векторов для пространств различных размерностей.

Теперь видно, что для двумерного пространства углы распределяются равномерно, для трёхмерного — пропорционально синусоидальной функции, а при повышении размерности распределение стремится к нормальному с постоянно уменьшающейся дисперсией. Для всех размерностей выше двух, мода распределения приходится на 90 градусов и доля взаимно ортогональных векторов увеличивается, по мере увеличения числа параметров. Самое же главное наблюдение — сонаправленных векторов (имеющих угол около 0 или 180 градусов практически не остаётся при достаточно высокой размерности пространства. Давайте будем считать более или менее похожими (сонаправленными, сравнимыми) векторы, имеющие угол мене 30 градусов (это вполне малый угол: $30^\circ = \pi/6 \approx 1/2 = \sin 30^\circ$ ). Тогда, при сравнении по двум критериям, похожей на какой-то выделенный вектор, окажется только треть всех случайных векторов. Использование трёх критериев позволит сравнивать с заданным вектором лишь $13\%$ всего множества, для четырёх критериев — уже $6\%$ , и каждое следующее добавление размерности будет уменьшать эту долю вдвое. Если мы будем строже и ограничим себя меньшим углом, доля векторов, считающихся похожими станет убывать ещё быстрее.

Таким образом, получаем векторную формулировку закона арбузной корки:

В пространствах высокой размерности почти все вектора ортогональны друг другу.

или эквивалентно: на вкус и цвет товарищей нет.

Сравнивайте разумно, не ищите в жизни нормальности и не бойтесь ненормальности. Сама математика подсказывает нам, что в сложном мире людей говорить можно лишь о степени подобия, но не о сравнении. Так что нет резона вести нескончаемые споры, в поисках истины, вместо этого, стоит прислушаться и постараться услышать иное мнение, увидеть взгляд из другого, сопряжённого, пространства, обогащая тем самым своё восприятие мира.

Мудрецы правы: все мы уникальны и в своей уникальности абсолютно одинаковы.

Приглашаю вас, первых читателей этой книжки, к вопросам, дополнениям и замечаниям, которые, без сомнения, сделают её точнее, богаче и интереснее.