Теория счастья. Термодинамика классового неравенства14.10.2018 18:18

Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

Опубликованные главы:

• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры

В этой главе мы порассуждаем о деньгах, рынках и энтропии, а также посмотрим на анимированные гифки, которых, увы, в книжке напечатать не получится.

Наблюдение Хонгрена:
Среди экономистов реальный мир зачастую считается частным случаем.

Экономика — большая, серьёзная, но своеобразная наука. Несомненно, она жизненно необходима, как дисциплина, изучающая реальное и важное явление нашего мира: экономическую действительность. Экономическая наука стремится к доказуемости и формализации, в ней много математики, подчас сложной и интересной. Однако открывая серьёзный экономический учебник, вы, скорее всего, обнаружите какие-то сравнительно несложные выкладки, готовые рецепты и кучу неформальных рассуждений в таком духе: «но на самом деле всё может быть не так и, вообще, как угодно, если на то будет воля ключевых игроков или правительства». В конце концов, может сложиться ощущение, что в этой дисциплине важнее интуиция, знание психологии и умение воспринимать общий контекст, чем точный расчёт и скурпулёзное рассмотрение деталей (речь об экономике, а не о бухгалтерии). Наконец, почти половина липовых диссертаций пишется именно по экономике, стало быть, не так уж и сложно наукообразно рассуждать на экономические темы. Попробуем и мы свои силы на этом поприще, благо, нигде так остро не воспринимается несправедливость этого мира, как в вопросе распределения богатства. К тому же, чем бы ни занимался человек, какой бы профессией ни владел, он вовлечён в экономику и её игры, от законов экономики, как и от законов физики не спрятаться.

Из всей массы задач, решаемых математической экономикой, мы рассмотрим лишь одну — каким образом получается так, что даже при равных условиях для всех участников рынка и справедливом обмене средствами бедных становится больше чем богатых и почему даже идеальное математическое общество оказывается склонно к финансовому неравенству. Ну, и попутно узнаем кое-что любопытное о математической статистике и распределениях случайных величин.

Я физик по образованию и по профессии, и моя профессиональная деформация выражается в своеобразном взгляде на мир, как на множество разнообразных физических систем и процессов. С точки зрения физика, реальный рынок — это существенно нестационарная открытая система, со множеством степеней свободы, в которой важную роль играют стохастические (случайные) процессы. В этом смысле рынок похож на предмет изучения таких разделов физики, как термодинамика и статистическая физика, в которых, ввиду невозможности рассмотреть всё неисчислимое количество деталей и поведение всех составляющих частей системы, переходят к обобщающим и измеримым её свойствам, таким как энергия, температура или давление. Неудивительно, что попытки термодинамического описания экономических систем и создания эконофизики предпринимаются уже более ста лет. Но вот беда: пока учёные рассматривают детали, обобщают полученные знания и ведут споры о фундаментальных законах, основной объект изучения — экономическая действительность, успевает поменяться до неузнаваемости. Её поведение как будто стремится сохранить, а то и увеличить свои неопределённость и непредсказуемость.

Хорошим примером служит двухвековая история использования технического анализа при игре на фондовой бирже. Когда появляется новый мощный инструмент, позволяющий нащупать скрытые закономерности и предсказать курс ценной бумаги или акции, он начинает приносить прибыль тем, кто его использует. Но вскоре рынок начинает «чувствовать» новых игроков и подстраиваться под их стратегию, точность предсказаний замечательного метода начинает падать и, спустя какое-то время, он попадает в большой список устаревших и не слишком надёжных инструментов. Ни современные гибкие самообучающиеся нейросетевые алгоритмы, ни сверхскоростные роботы-трейдеры, совершающие миллионы операций в минуту, не поменяли за минувшие два десятилетия основное свойство биржевой игры — её непредсказуемость. И до сих пор основными достоинствами профессионала в этой отрасли являются воля, выдержка характера, несклонность к азарту… ну, или владение биржей. Всё как в казино, где игры основаны на чистой случайности! С одной стороны, это, конечно, обидно, а с другой — даёт повод постоянно совершенствовать методы и подходы. Когда-то и теория вероятностей и математическая статистика родились из попыток анализа азартных и экономических игр и только потом нашли применение почти во всех естественных науках.

Мы в дальнейших рассуждениях будем говорить о деньгах, но эта привычная повседневно используемая категория на удивление сложна и неоднозначна. Смысл и ценность денег зависит от множества факторов, и называя вне контекста некую денежную сумму, мы ничего не говорим о её реальной ценности. Это отличает денежные величины от большинства физических величин, описывающих наш мир и здорово мешает проводить строгие рассуждения в экономике. Но цель нашего разговора: математические основы законов подлости, повседневных, понятных и простых. Поэтому в дальнейшем мы будем говорить о неких «рублях», имея в виду формальный билетик или монетку, и подразумевая, что чем больше этих «рублей» у кого-то, тем он «богаче». Прочие же рассуждения о покупательской способности, нематериальных или неликвидных ценностях, о «не в деньгах счастье», наконец, мы оставим за рамками разговора.

Подходите, всем хватит!

Начнём с анализа справедливости некоторых простых стратегий раздачи известного количества денег конечной группе людей.

Первая, самая очевидная стратегия: «взять всё, да и поделить», то есть выделить каждому члену группы по равной доле общей суммы. Такое распределение называется вырожденным, оно имеет индекс Джини равный нулю и соответствует кривой равенства на диаграмме Лоренца.

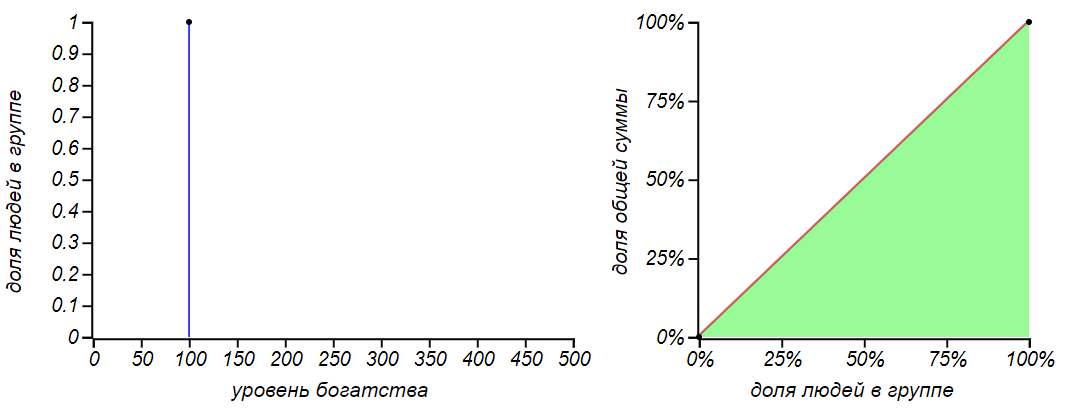
Абсолютно справедливое вырожденное распределение денег: у всех всё поровну.

Прекрасный вариант! Назовём его «стратегией Шарикова» в честь героя повести Михаила Булгакова «Собачье сердце», который именно таким способом предлагал решить все экономические вопросы.

Вторая, более реалистичная стратегия заключается в многократной раздаче всем по одному рублю в случайном порядке. Кому как повезёт. Можем назвать эту стратегию «пуассоновской», поскольку именно таким образом распределяются по временной шкале независимые случайные события в процессе Пуассона. Для группы из $n$ человек вероятность каждого из участников получить рубль составляет $1/n$ . После раздачи таким образом $M$ рублей, каждый должен получить сумму равную количеству таких «положительных» исходов. Функция вероятности для подобной суммы хорошо известна — это биномиальное распределение, похожее на колокол, симметрично разбегающийся вокруг среднего значения $M/n$ . Обычно с ним знакомят на примере вычисления вероятности получить указанную сумму, бросая игральные кости. Для больших значений $M$ биномиальное распределение становится практически неотличимым от нормального. Давайте посмотрим как будет меняться, по мере раздачи денег, распределение денег в группе и его справедливость.

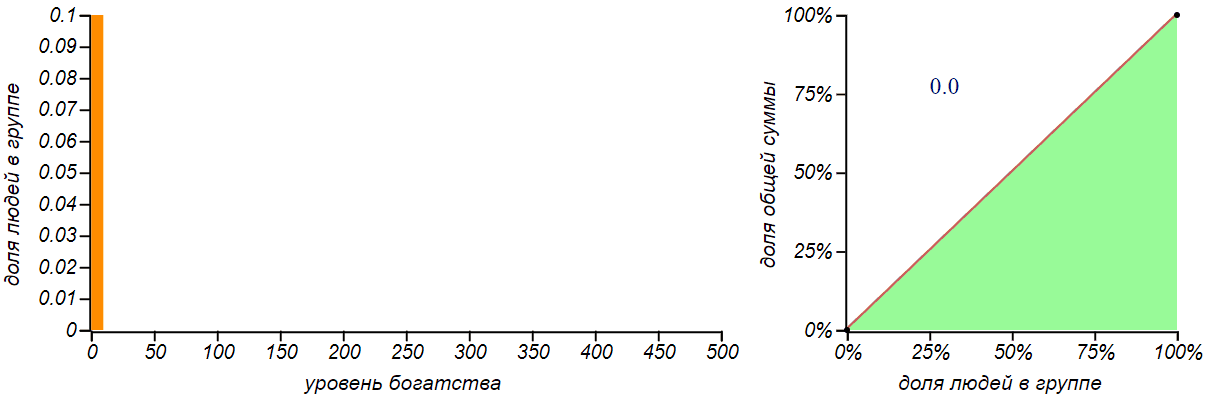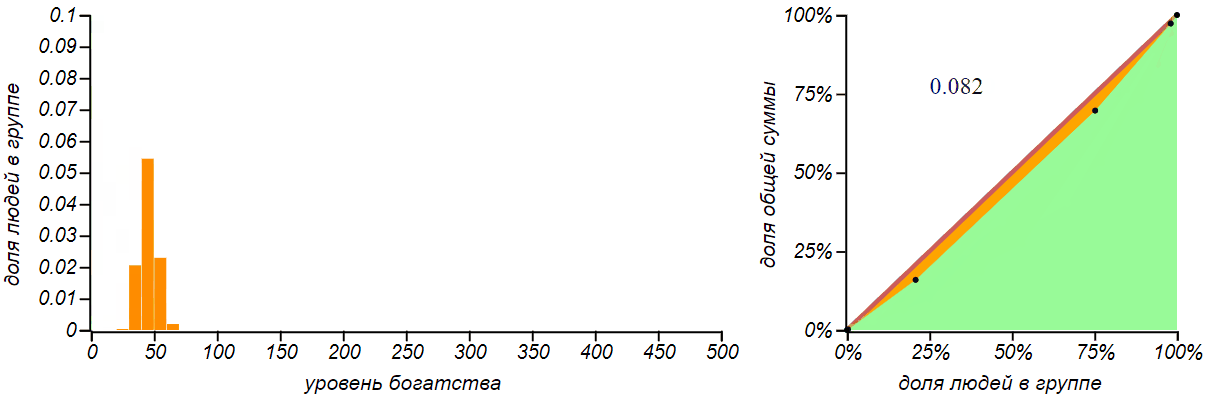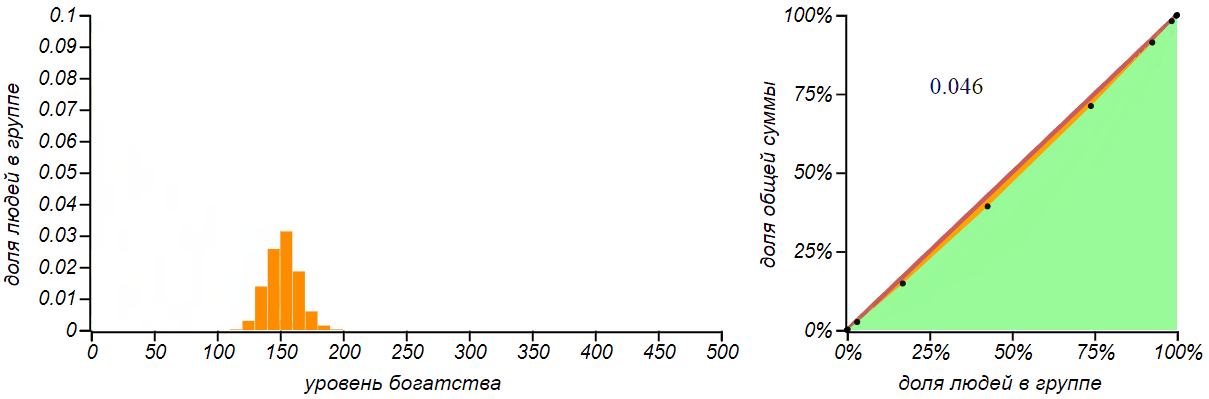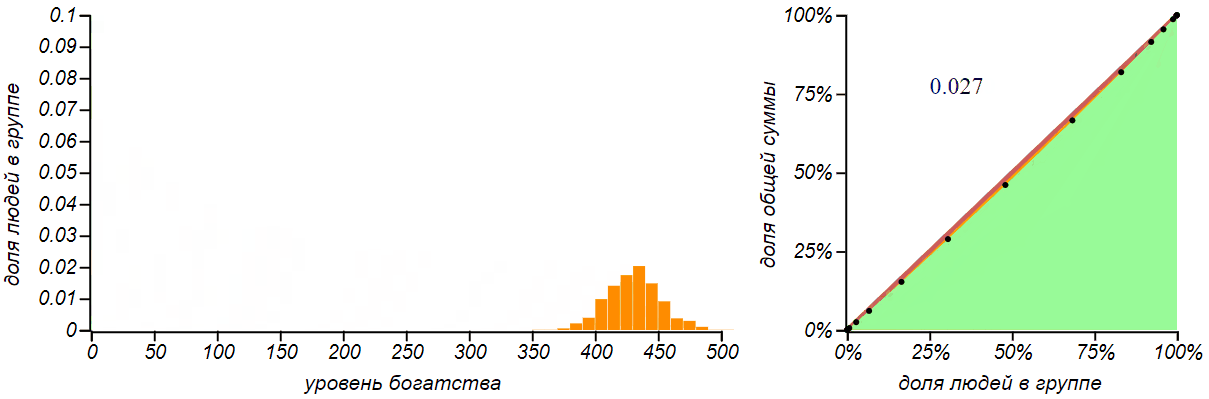
Результатом раздачи денег по принципу «на кого бог пошлёт» является биномиальное распределение. Чем больше денег мы раздаём, тем больше становится значение среднего и разброс, но вероятность не получить ничего практически исчезает.

Алгоритм пуассоновской стратегии

Исходные данные: xs — массив из n элементов, заполненный нулями, M — общее количество денег в системе.
Повторить M раз
    i <- случайное целое от 1 до n
    xs[i] <- xs[i] + 1

Это распределение, с точки зрения справедливости, очень неплохо выглядит, более того, оно становится тем справедливее, чем больше денег мы раздаём публике! Просто замечательно! Жаль, что общество устроено не так и дождь из денег не сыплется на всех нас поровну.

Для полноты картины, давайте рассмотрим ещё одно простое искусственное распределение денег — равномерное. При таком распределении бедных будет столько же сколько и богатых.

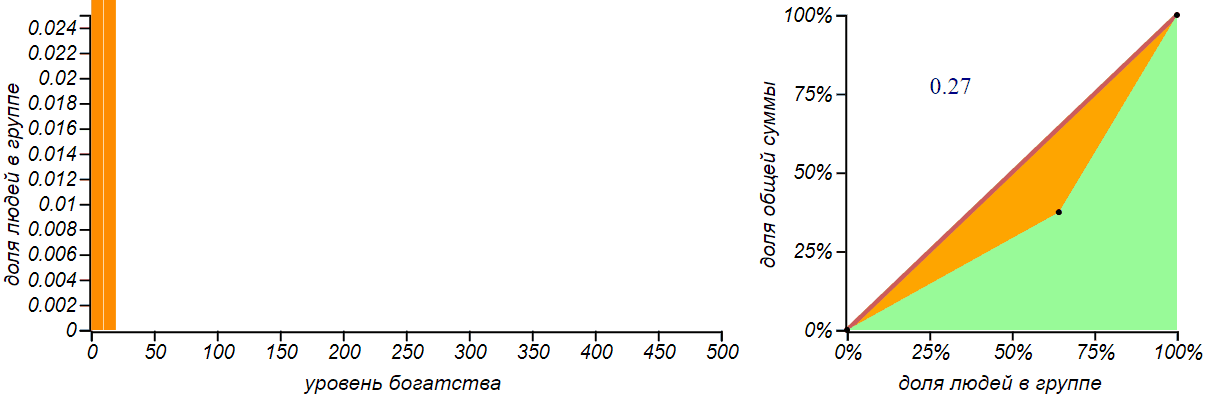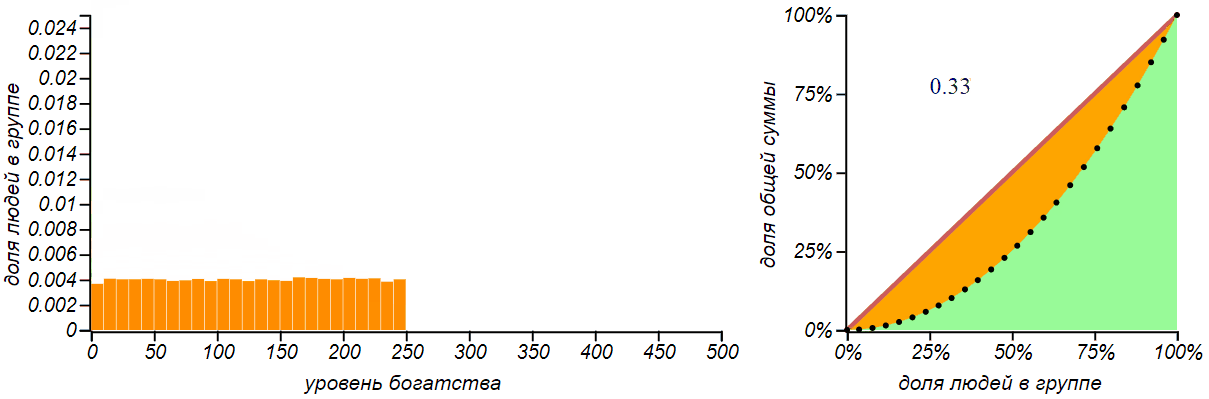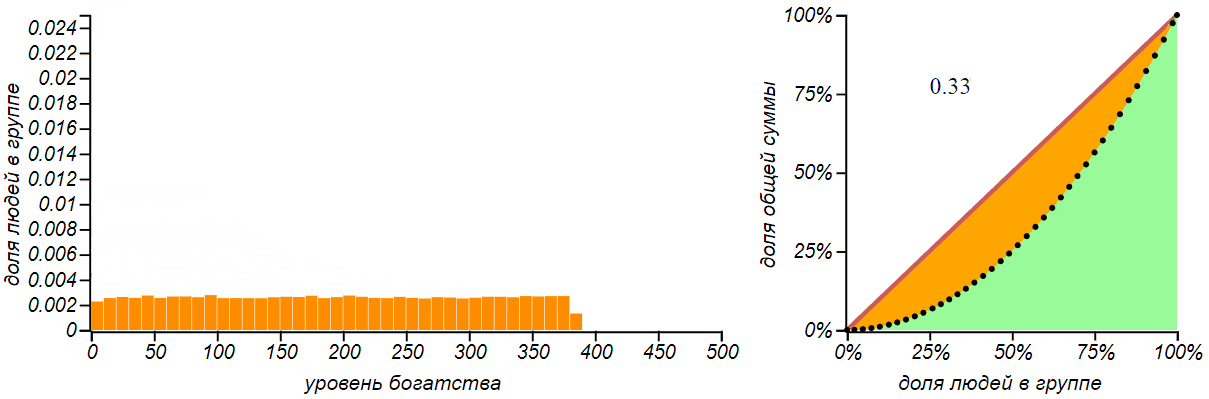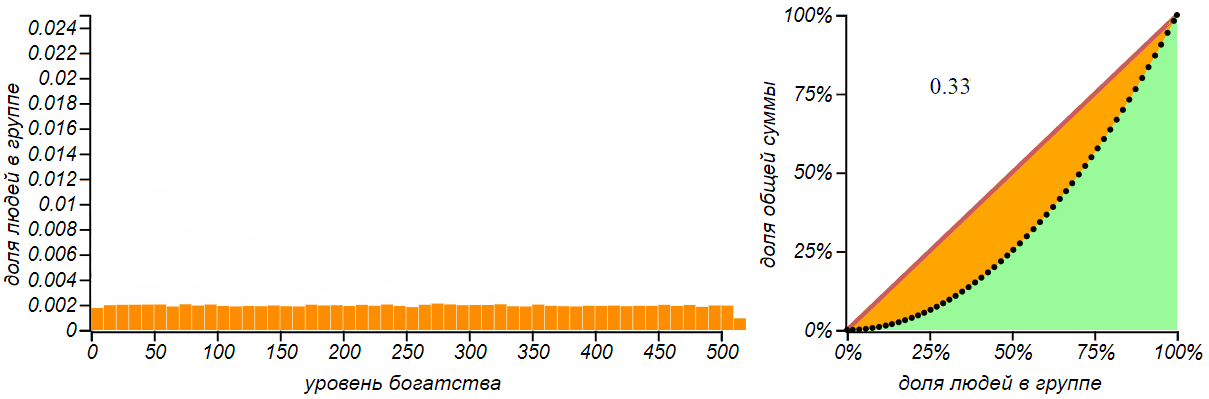
Равномерное распределение не означает, что деньги распределяются по всем равномерно. При таком распределении число богатых, бедных и середнячков одинаково, но деньги в основном принадлежат богатым.

Алгоритм стратегии равномерной раздачи

Исходные данные: xs — массив из n элементов, заполненный нулями, M — общее количество денег в системе.
Для каждого элемента x из массива xs
    x <- случайное целое от 0 до M/n

Для равномерного распределения кривая Лоренца представляет собой квадратичную параболу, а если левая граница распределения равна нулю, то эта парабола независима от положения правой границы, и индекс Джини для всех таких распределений равен в точности $1/3$ . Такое значение индекса (но не такое распределение!) был, например у экономики Австралии в 2000-е годы — это вполне неплохой показатель.

Однако рынок есть рынок! Рассмотренные выше распределения хороши, но требуют специальных условий для своего возникновения. Если дать людям волю обмениваться деньгами, менять деньги на услуги, копить их и проматывать в одну ночь, идеальные распределения потеряют устойчивость и превратятся в какие-нибудь другие.

Новая экономическая политика!

Рассмотрим группу из $n$ человек. В результате революции раздадим всем участникам эксперимента по равной денежной сумме — по $m$ рублей каждому, получив самое справедливое шариковское распределение средств в обществе. Теперь предоставим им свободу богатеть и беднеть по воле собственной судьбы и построим примитивную модель рынка. Попросим кого-нибудь, случайно выбранного, отдать один рубль любому человеку из группы, так же выбранному случайно. Скажем, что это приобретение некой услуги по фиксированной цене. Распределение богатства ожидаемо изменится: у кого-то денег станет меньше, у кого-то больше. Станем повторять процедуру обмена снова и снова и посмотрим на то, как будет изменяться распределение богатства в группе.

Разумно перед проведением эксперимента поразмыслить, что же мы ожидаем увидеть. Обмен деньгами между участниками происходит равновероятно, как в случае пуассоновской стратегии раздачи денег, но в тоже время игроки и теряют деньги, причём по такому же пуассоновскому принципу и с такой же интенсивностью. Таким образом, можно предположить, что как положительные, так и отрицательные приращения будут нормально распределены и расположены симметрично относительно нуля. Каждый игрок, в конечном итоге, будет получать разность этих приращений, которая для двух нормально распределённых случайных величин будет тоже нормально распределена, в данном случае, вокруг нуля, так как потери и выигрыши симметричны.

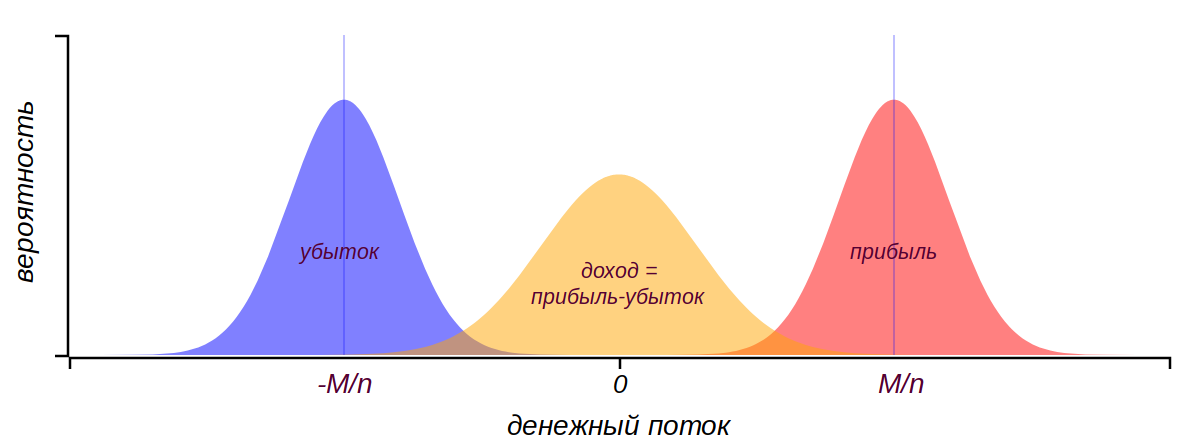
После множества обменов каждый игрок получит и потеряет сумму, подчиняющуюся распределению, близкому к нормальному. Суммарный доход также будет нормально распределён вокруг нуля.

Таким образом, мы получаем классическое случайное блуждание с нормально распределёнными приращениями и можем ожидать некой диффузии средств вокруг среднего значения $m$ . Функция вероятности должна размываться, увеличивая дисперсию при неизменном среднем значении. Вроде бы, всё просто.

Но есть нюанс. Если, по каким-то причинам, у кого-либо из группы не осталось средств, он не сможет приобретать услуги, отдавая деньги, но, в тоже время, может их получать. Возможное значение благосостояния ограничено слева нулём, а значит диффузия богатства не сможет распространяться бесконечно и наблюдаемая функция вероятности, рано или поздно, перестанет быть симметричной.

Есть ещё один нюанс. Количество денег в нашей замкнутой системе ограничено и неизменно, это значит, что случайные блуждания не независимы. Какой-нибудь везучий игрок сможет получить очень большие суммы и уйти от ансамбля очень далеко, но только если общая масса обеднеет. Участников эксперимента стягивает невидимой сетью закон сохранения денег в системе. К чему же будет стремиться распределение денег таких условиях? Похоже, ответ не столь очевиден, как может показаться на первый взгляд, давайте обратимся к имитационному моделированию и посмотрим что у нас получится.

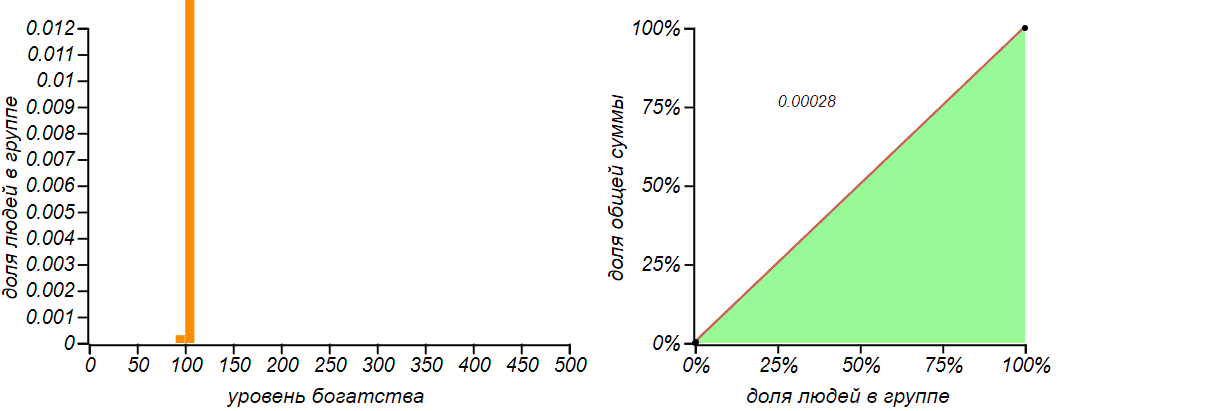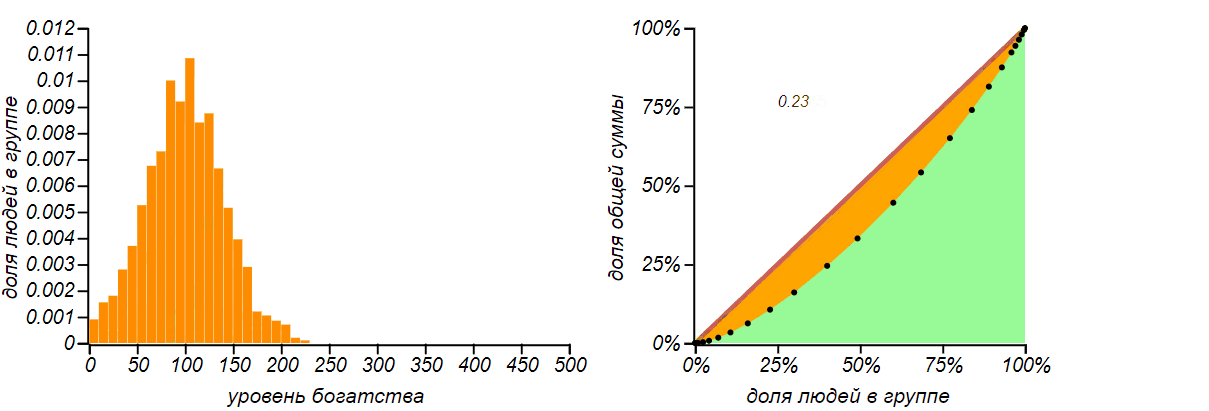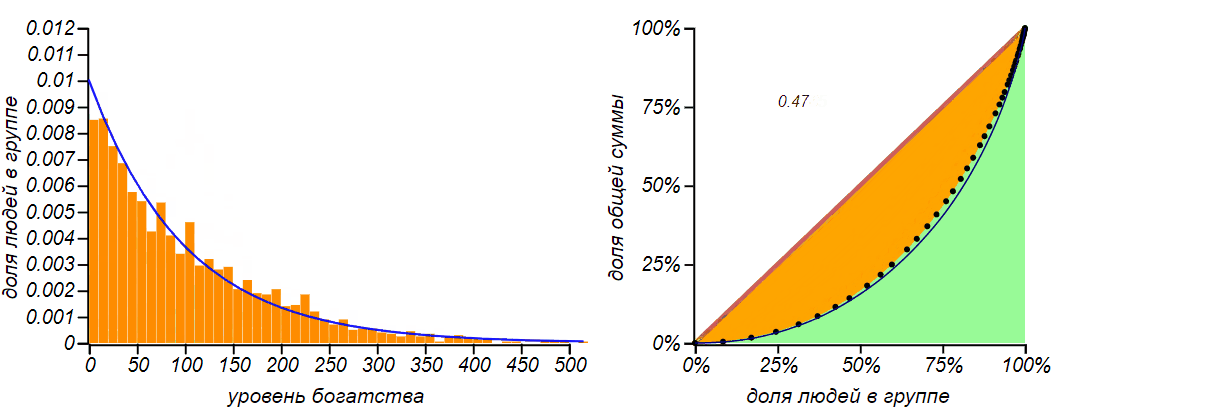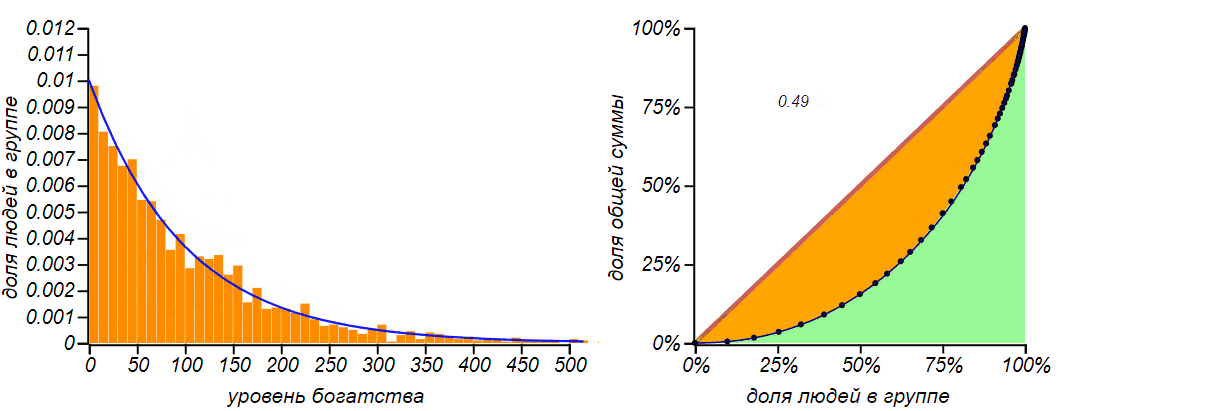
Результат имитационного моделирования для обмена равным количеством денег для и . Сначала, действительно, наблюдается явление, подобное диффузии, но по мере достижения функцией вероятности левой границы, распределение стремится к характерной несимметричной и не очень справедливой форме с коэффициентом Джини близкому к .

Алгоритм обмена равными суммами

Исходные данные: xs — массив из n элементов, инициализированный значениями m.
Повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        j <- случайное целое от 0 до n
        xs[i] <- xs[i] - 1
        xs[j] <- xs[j] + 1

Если эту книжку читает физик, то он сможет уверенно предположить что это может быть за распределение, он назовёт его распределением Гиббса. Внимательный читатель может вспомнить, что мы уже встречались с подобной картинкой и с таким индексом Джини, когда рассматривали фрустрацию во время ожидания автобуса. Тогда мы рассматривали распределение интервалов между пуассоновскими событиями, которое описывалось экспоненциальным распределением. Оба этих проницательных господина будут правы, называя разными именами одно и то же замечательно распределение.

Люди — молекулы

Распределение Гиббса — это из области статистической физики. Здесь описываются свойства систем, называемых красивым словом «ансамбль», которые состоят из великого множества взаимодействующих элементов, чаще всего, частиц. В ансамбле можно выделять произвольные подсистемы (например, отдельные частицы или их группы) и ставить им в соответствие некие функции состояния (это могут быть обобщённые координаты, скорости, концентрации, химические потенциалы и многое другое). С помощью методов статистической физики удаётся объяснить и вычислить параметры самых разнообразных явлений: химических и каталитических процессов, турбулентности, ферромагнетизма, поведения жидких кристаллов, сверхтекучести и сверхпроводимости и многих других.

Распределение Гиббса отвечает на вопрос: какова вероятность встретить некое состояние подсистемы, если даны а) энергия состояния, б) макроскопические (условно говоря, глобальные) свойства системы, такие, например, как температура и в) известно, что система находится в термодинамическом равновесии? Оно может быть схематично выражено следующим образом:

$p_{\mathrm{Gibbs}(T)}(x) = С e^{-\frac{E(x)}{kT}},$

где $x$ — некое состояние подсистемы, $E(x)$ — энергия этого состояния, $T$ — абсолютная температура системы (или её аналог), а $C$ и $k$ — величины, необходимые для нормировки и соответствия размерностей. Условие равновесия очень важно, оно означает, что из рассмотрения исчезает время и что вся система окажется в наиболее вероятном своём состоянии для заданных условий.

Строгий вывод выражения для распределения Гиббса нам здесь не нужен, вместо него я хочу показать красивейшее чисто математическое рассуждение, приводящее к его экспоненциальной форме. Поскольку рассматриваются части системы, которые в сумме дают всю систему, то и в качестве их характеристики стоит выбрать какую-либо аддитивную величину, то есть такую, чтобы её значение для ансамбля было арифметической суммой значений его частей. В качестве такой величины в механике можно использовать энергию. С другой стороны, мы вычисляем вероятность наблюдать некоторое состояние системы, а вероятность величина мультипликативная, то есть, если систему можно разбить на части, то вероятность наблюдать все эти части одновременно будет равна произведению вероятностей для состояния каждой из частей. Таким образом, нам нужна функция, превращающая аддитивную величину в мультипликативную. Таким свойством обладает только показательная функция $a^x$ , сумму аргументов превращает в произведение значений: $a^{x+y} = a^x a^y.$ Ну, а из всех показательных функций, наиболее удобной является экспонента, поскольку она очень хорошо ведёт себя при интегрировании и дифференцировании.

В нашей модели рынка мы имеем аддитивную величину — количество денег у каждого игрока, это аналог энергии. При описанном нами обмене, эта величина, как и энергия в физической системе, сохраняется. А какой смысл здесь у температуры? Это просто выяснить, посмотрев на выражение для плотности вероятности экспоненциального распределения:

$p_{\mathrm{Exp}(\lambda)}(x) = \lambda e^{-\lambda x},$

и вспомнив, что среднее значение для него равно $1/\lambda$ . Так как число игроков в ходе торгов неизменно, то сохраняется и среднее арифметическое количество денег у игроков, равное первоначально раздаваемой сумме $m$ . Отсюда естественным образом следует, что $\lambda = 1/m$ , значит в роли температуры в нашей экономической модели выступает среднее количество денег у игроков. В «разогретом» рынке с большой ликвидностью мы сможем наблюдать и больший разброс в уровне благосостояния, чем в «холодном», ведь в экспоненциальном распределении дисперсия равна $1/\lambda^2$ . Как говорил Остап Бендер в «Золотом Телёнке» И. Ильфа и Е. Петрова: «Раз в стране бродят какие-то денежные знаки, то должны быть люди, у которых их много.»

Если быть совсем точным, и вспомнить, что деньги в нашем эксперименте это величина дискретная, то мы наблюдаем геометрическое распределение — дискретный аналог экспоненциального. Оно встречается в задаче подсчёта числа неудач до первого выигрыша при подбрасывании монеток разной степени честности. Эти два распределения подобны и становятся неотличимы при уменьшении вероятности выигрыша. В нашем эксперименте шансы получить рубль равны $1/1000$ , это достаточно мало для того, чтобы называть распределение экспоненциальным.

Осталось разобраться с равновесностью итогового состояния рынка. Термодинамическое равновесие можно описать разными способами. Во-первых, равновесным должно быть стационарное состояние, в котором система может находиться неограниченно долго, не изменяя своих макроскопических параметров, и не образуя внутри себя упорядоченных потоков вещества и энергии. Во-вторых, оно должно быть устойчивым, то есть, если вывести систему из равновесия, она будет стремиться к нему вернуться. В-третьих, это наиболее вероятное состояние системы, чаще всего наблюдаемое, в которое со временем система будет стремиться попасть из любого другого, неравновесного. Наш эксперимент демонстрирует эти критерии равновесности: придя к экспоненциальному распределению, система в нём и остается, к тому же, в эксперименте легко убедиться, что из любого произвольного распределения мы, по истечении какого-то времени, снова придём к экспоненциальному. Но это ещё не доказательство, а только намёк, что мы, скорее всего, имеем дело с равновесием. Нужен какой-то формальный измеримый критерий, который однозначно указал бы нам, что система равновесна без необходимости ждать бесконечно долго или перебирать все возможные первоначальные распределения. Это был бы полезный критерий, который можно было бы применять и к реальному рынку, без необходимости проводить рискованные эксперименты на живых людях.

Дао выраженное словами — не истинное Дао

Размышления о равновесии привели физиков к понятию энтропии, которое постепенно вышло за пределы термодинамики и так понравилось ученым всех направлений, философам и широкой публике, что теперь энтропия получила ореол загадочности, непостижимости и бог знает ещё чего. Простое и специальное, в сущности, понятие приобрело в сознании широких масс репутацию необъяснимо управляющей миром концепции. Это связано с тем, что термодинамика — универсальная наука, описывающая на очень высоком уровне абстракции системы самой разнообразной природы: от физических, химических и биологических до социальных, экономических и даже чисто гуманитарных. После школьного курса, правда, остаётся ощущение, что термодинамика — это про скучный идеальный газ, какие-то поршни и невозможный цикл Карно. Такое весьма одностороннее представление связано с тем замечательным фактом, что термодинамика, будучи одной из самых абстрактных и универсальных разделов естествознания, элегантно решает прикладные задачи, понятные школьникам и полезные в промышленности. Этого не скажешь, например, о теории категорий или топологии — тоже весьма абстрактных, универсальных и, несомненно, полезных дисциплинах, но в повседневных задачах почти не встречающихся.

Итак, энтропия. Создателю термодинамики Клаузиусу, а позже Гиббсу и Больцману потребовалась количественная характеристика равновесности, говорящая о вероятности наблюдать указанное состояние системы или её частей. Причём, эта величина, отражающая вероятность, мультипликативную по своей природе, должна быть аддитивной функцией состояния, чтобы можно было бы вычислить её для системы, складывая значения, вычисленные для её частей. Когда мы искали подходящую функцию для распределения Гиббса, мы исходили из того, что она должна превращать аддитивный аргумент в мультипликативное значение. При поиске выражения для энтропии мы нуждаемся в функции, мультипликативной по аргументу и аддитивной по значению — это логарифмическая функция, обратная показательной. Энтропия состояния сложной системы может быть выражена как ожидаемое значение для логарифма вероятности наблюдения состояния всех её частей, или, по Больцману, как логарифм числа способов, которым можно реализовать это состояние системы. При этом более вероятному состоянию соответствует большее значение энтропии, а равновесному — максимальное из возможных.

Число способов реализовать то или иное состояние зависит и от числа ограничений или условий, при которых это состояние может реализоваться. Чем меньше таких ограничений, тем более вероятным является состояние и тем больше значение его энтропии. Эти ограничения и условия имеют смысл информации о состоянии. Отсюда возникла идея о том, что энтропия отражает степень нашего незнания о системе: чем меньше нам о состоянии известно, тем больше его энтропия. Позже Шеннон обобщил это понятие для любых систем, содержащих в себе информацию, в том числе и для распределений случайных величин. Вот что у него получилось: для случайной величины $X$ , определяемой функцией вероятности $p(x)$ энтропия определяется следующим образом:

$H(X) \equiv -\mathrm{M}(\ln(p(x))) = -\sum{p(x)\ln(p(x))},$

где суммирование производится по всем значениям $x$ , в которых $p(x) > 0$» />. Таким образом, мы имеем возможность вычислить энтропию состояния любой сложной системы, имея её статистическое описание.</p>

<p>Вот как изменяется энтропия по мере того как модель нашего рынка приходит к равновесию.</p>

<div><img src=

Рост энтропии по мере приближения рынка к равновесному состоянию. Горизонтальной линией на правом графике показано теоретическое значение энтропии для экспоненциального распределения, равное $1-\ln(\lambda)$ . Промежуточная «полочка» соответствует периоду, в течение которого распределение проходило стадию диффузии и было похоже на нормальное.

Таким образом, каждому распределению: задаваемому аналитически или полученному экспериментально в виде гистограммы, можно поставить в соответствие положительное число — его энтропию. Значит распределения можно сравнивать между собой, определяя более или менее равновесные и вероятные для заданных условий. Более того, для некоторого класса распределений можно выделить распределение с максимальной энтропией, причём, только одно. Классы определяются ограничениями, или мерой нашего знания о статистических свойствах системы. Приведём несколько примеров:

Знакомые всё лица! Это очень часто используемые распределения, которые статистики применяют к широчайшему классу задач. Их универсальность обусловлена именно тем, что они, имея максимальную энтропию, наиболее вероятны и наблюдаемы. К ним, как к равновесным, стремятся многие распределения реальных случайных величин. Самым свободным от ограничений среди всех прочих является нормальное распределение: оно требует минимума информации о случайной величине. Меньше уже не получится: если мы укажем лишь среднее значение, то стремясь увеличить энтропию, распределение «размажется» по всей числовой оси. Зато, если мы знаем лишь среднее значение, но при этом ограничим случайную величину положительными значениями, то равновесное распределение будет однозначным — экспоненциальным. Именно этот случай мы и наблюдали в нашем эксперименте с рынком. Нам заранее было известно лишь сколько денег мы выдали каждому игроку и то, что количество денег в системе неизменно, это фиксировало среднее значение. А так как деньги у нас величина положительная, вероятнее всего, в равновесии мы получим экспоненциальное распределение богатства с индексом Джини равным $1/2$ .

Существует множество модификаций описанной нами модели: обмен может происходить не одним рублём, а случайной величиной, ограниченной состоянием дающего, при этом можно давать деньги не какому-то одному игроку, а распределять случайным образом. Пока мы не вводим в игру новых параметров все эти модификации не меняют форму равновесного распределения богатства — оно остаётся экспоненциальным. В этом можно убедиться с помощью имитационного моделирования, но приводить картинки для различных способов обмена не интересно — они все одинаковы. Многие исследователи отмечали эту особенность моделей рынка. Интересна модель построенная Драгулеску и Яковенко из Мерилендского университета, в которой игроков объединяют в некие компании и далее имитируется взаимодействие компаний с игроками-работниками и игроками-покупателями. Но и в этом сложном случае равновесным является экспоненциальное распределение, безразличное к выбираемым параметрам модели.

Чтобы продемонстрировать универсальность принципа максимума энтропии давайте искусственно ограничим сверху уровень богатства отдельного игрока, запретив ему получать деньги, если у него уже есть некая фиксированная сумма. Равновесное распределение, конечно же, изменится. А в случае, если правая граница будет равна удвоенному среднему значению, то мы приходим к случаю, описанному в первом ряду таблицы. Действительно, ограничивая случайную величину конечным отрезком и не указывая больше ничего, мы не можем предположить никакого другого ожидаемого значения среднего, кроме середины этого отрезка. Следовательно, равновесным распределением при таком варианте должно быть равномерное. Давайте проверим, так ли это?

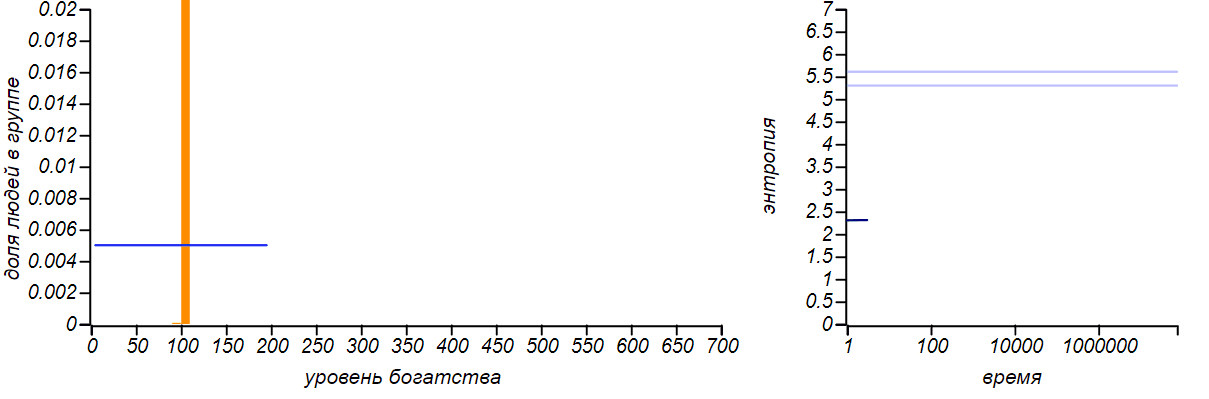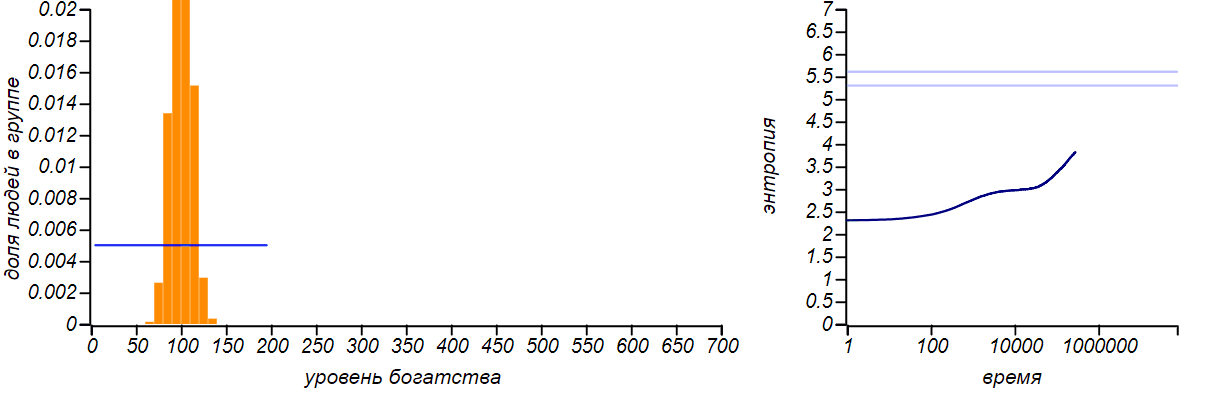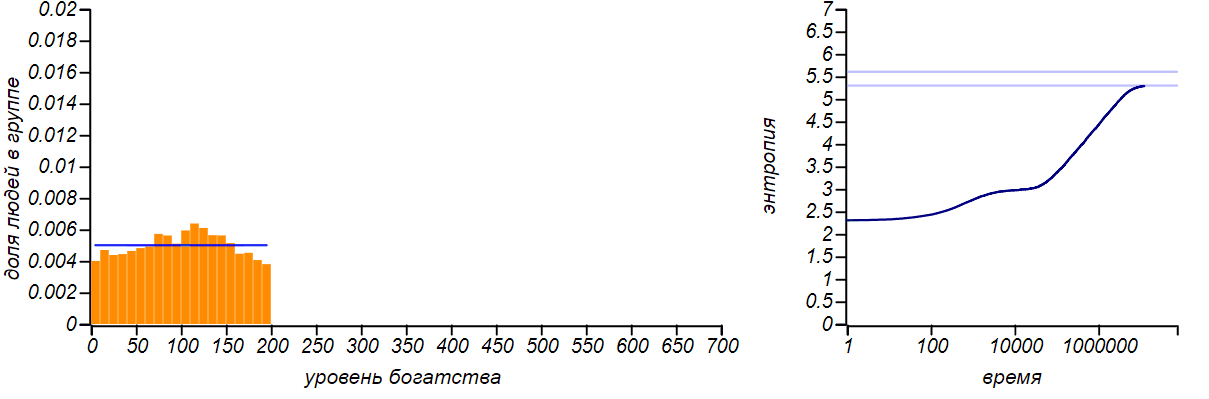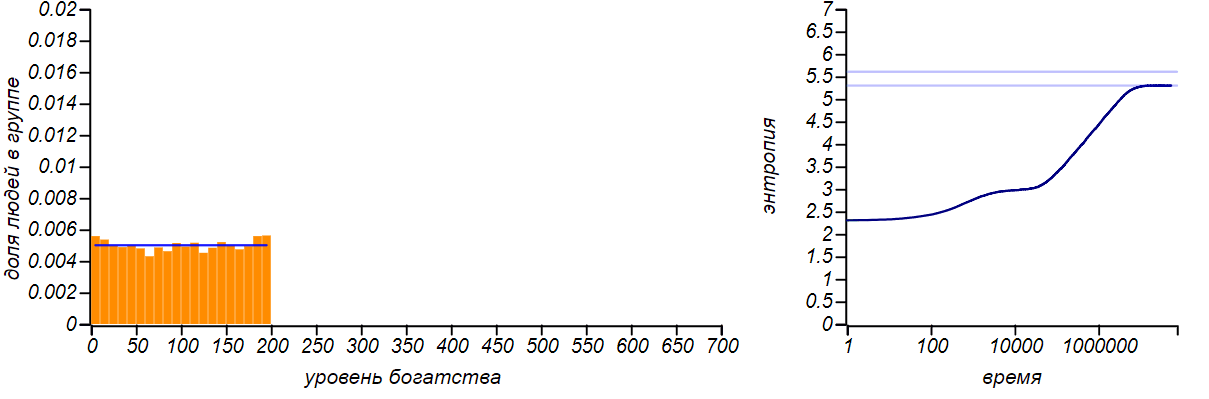
Вот что происходит при ограничении сверху возможного уровня богатства игроков, причём, таким образом, что верхняя граница ровно вдвое превышает среднее значение. Согласно принципу максимальной энтропии, равновесным распределением должно быть равномерное. Горизонтальной линией на правом графике показано теоретическое значение энтропии для равномерного распределения.

Алгоритм обмена равными суммами с ограничением сверху

Исходные данные: xs — массив из n элементов, инициализированный значениями m, xMax — максимальная разрешённая сумма.
Повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        j <- случайное целое от 0 до n
        если xs[j] < xMax
            xs[i] <- xs[i] - 1
            xs[j] <- xs[j] + 1

А что будет при нарушении симметрии, то есть, если мы сдвинем правую границу вправо или влево?

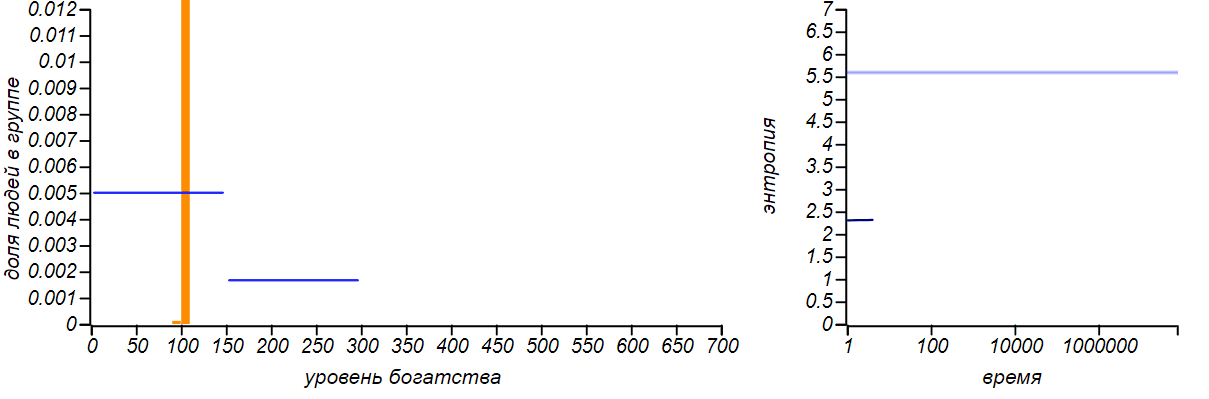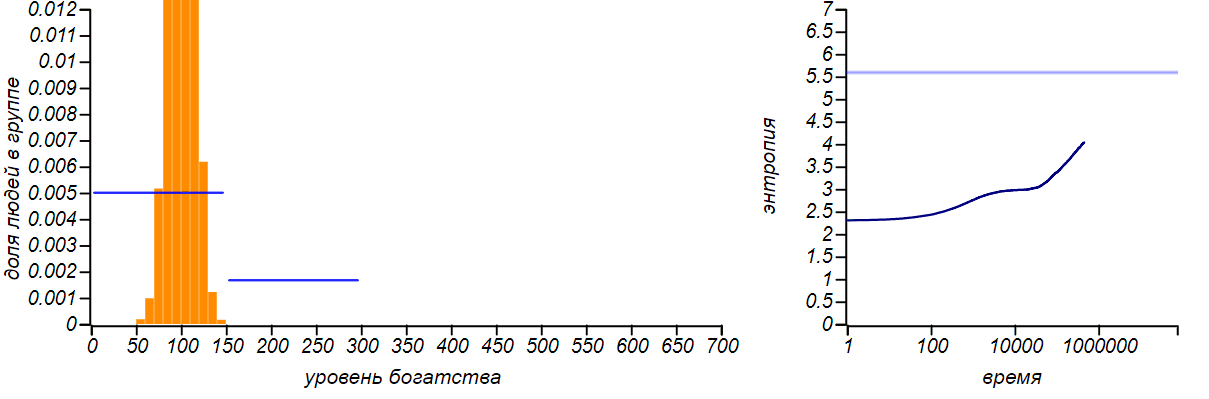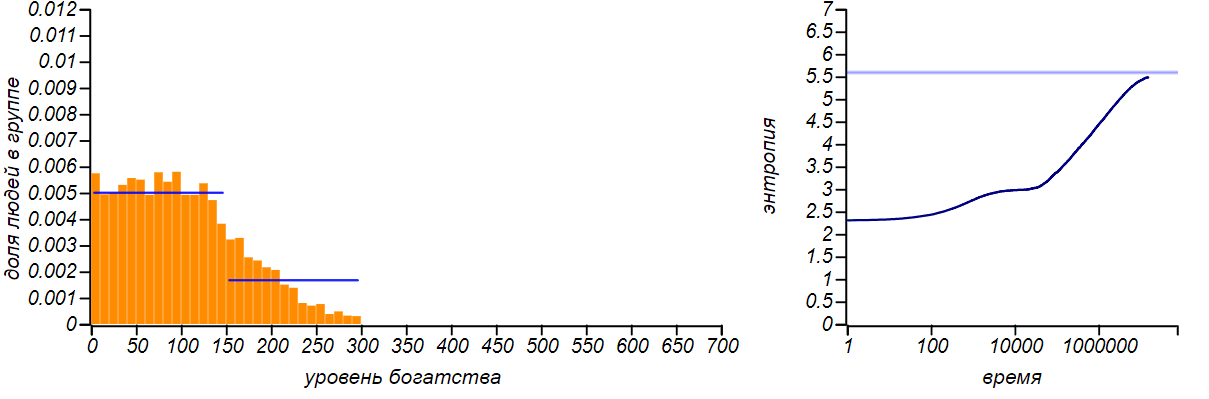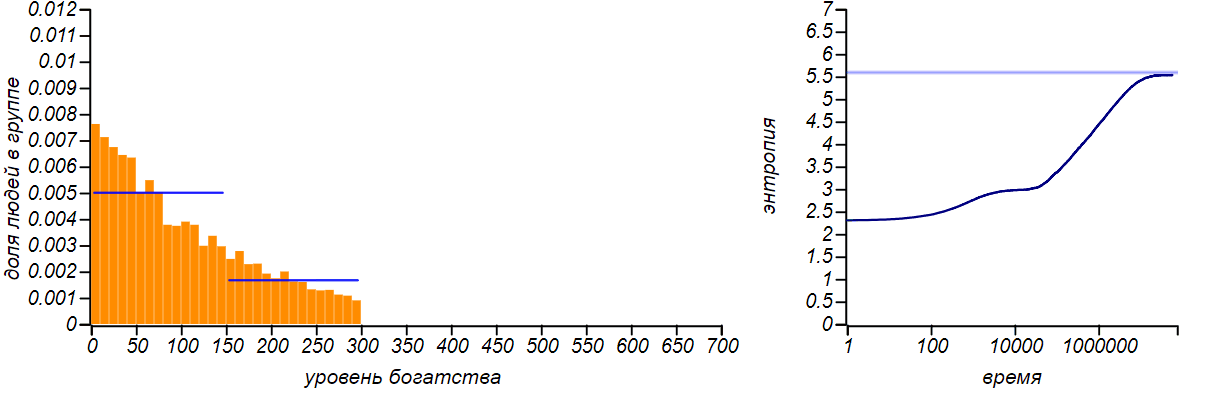
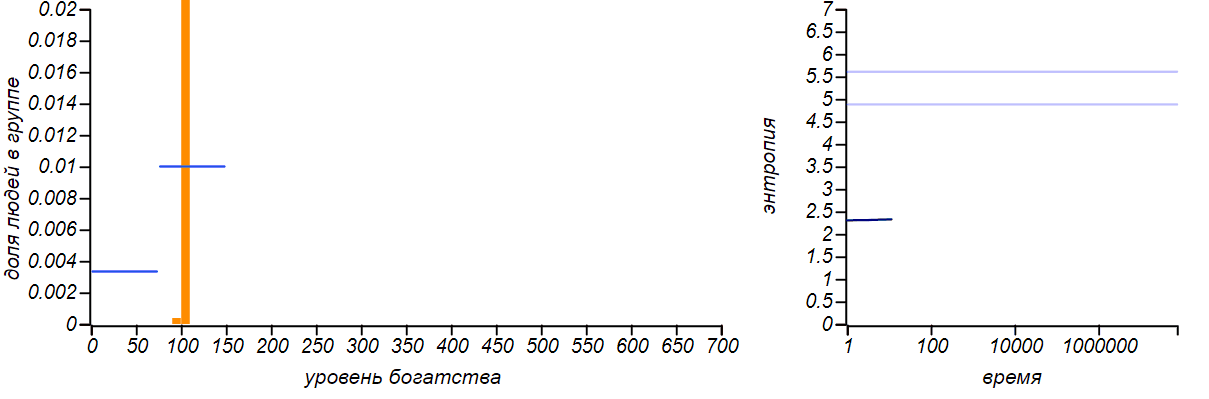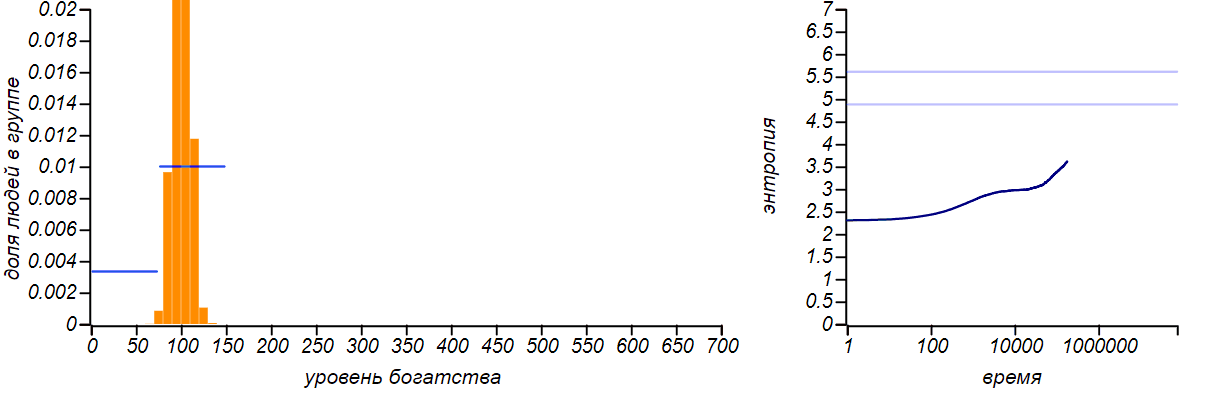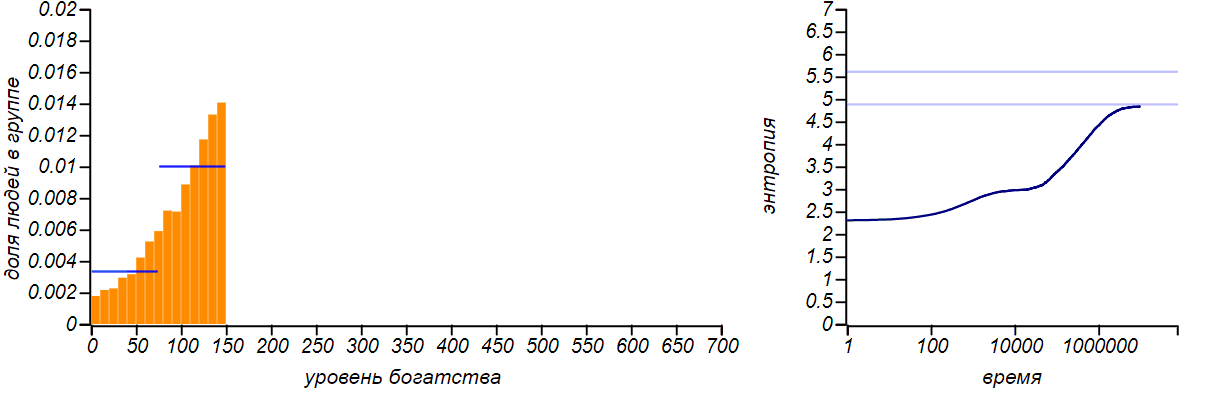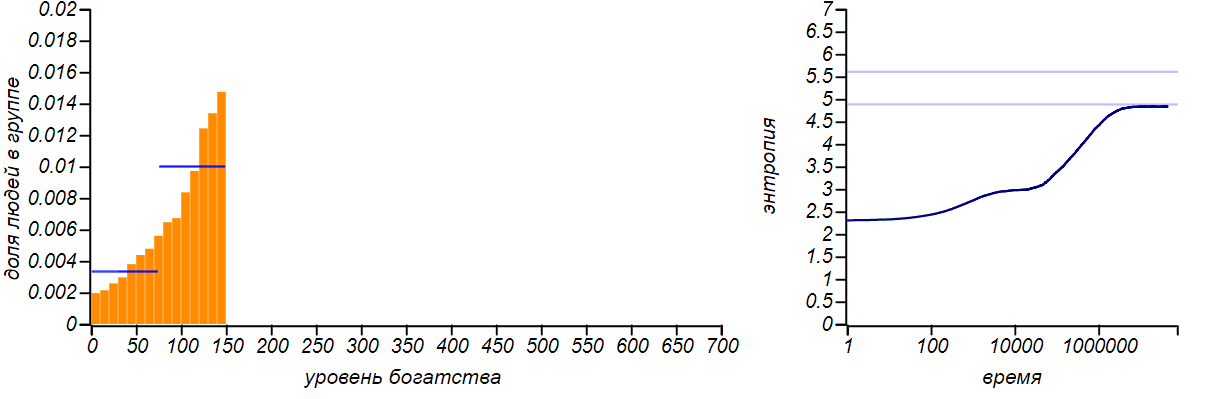
Варианты несимметричных ограниченных распределений в сравнении с распределениями Бернулли, соответствующими смещению среднего значения. Горизонтальные линии на графиках энтропии указывают теоретические значения для энтропии распределений Бернулли.

Распределение достатка перестало быть равномерным, приобретя форму ограниченного экспоненциального. При смещении правой границы влево в равновесии богатых игроков стало больше, чем бедных. Если мы «загрубим» гистограмму, оставив лишь два столбца, то получим распределение Бернулли, показывающее какова вероятность оказаться условно «бедным» или «богатым». Когда значения случайной величины ограничены всего двумя значениями, распределение Бернулли — единственный выбор, он же, естественно, доставляет максимум энтропии. Но обратите внимание на то, что энтропия наших модельных распределений стремится именно к тем значениям, которые предсказываются распределением Бернулли. Коэффициенты Джини для двух этих случаев равны $0.43$ и $0.2$ , соответственно.

Загадочная и могущественная энтропия — это, конечно, круто и, возможно, даже убедительно. Но почему же при симметричном обмене, бедных становится больше, чем богатых? Почему мода равновесного распределения равна нулю? Надо, как говорят физики, разобраться в кинетике процесса, то есть в судьбе отдельных частиц. Мы не ошиблись, предположив, что модель случайного блуждания описывает изменение состояния отдельного участника торгов: он с равной вероятностью совершает шаги как вверх, так и вниз. А для случайного блуждания выполняется один знаменитый закон подлости: проклятие игрока. Напомню, что он состоит в том, что при достаточно долгом наблюдении, случайно блуждающая частица обязательно окажется в любом наперёд указанном месте. Причём расстояние на которое частица удалится от какой-либо начальной точки пропорционально квадратному корню от числа шагов. Всё это приводит к тому, что если частица начинает свой путь вблизи нуля, то она с высокой вероятностью его достигнет, а так как ноль в нашей задаче — это непроницаемая граница, то она будет вынуждена вновь и вновь начинать свой путь около нулевой точки, испытывая пресловутое проклятие. По мере удаления частицы от нуля, вероятность к нему вернуться уменьшает