Теория счастья. Случайности неслучайны15.12.2018 15:34

Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

В этой главе мы порассуждаем о предопределённости полёта монетки, о топографических картах, о математических катастрофах и о природе случайности. А по пути заглянем в такие разделы математики, как теория мер и теория динамического хаоса.
Разговор о законах подлости, как источнике житейских неурядиц, часто начинается со знаменитого закона бутерброда. Он просто формулируется, легко проверяется и широко известен:

Бутерброд всегда падает маслом вниз.

Понятно, что слово «всегда» здесь — это преувеличение. Легко представить себе условия, в которых бутерброд упадет, оставив намазанную маслом сторону в сохранности. Что же люди понимают, под этим законом? Скорее всего, что бутерброд падает маслом вниз достаточно часто, чтобы это было заметно. Но чаще ли происходит неблагоприятный исход падения, чем благоприятный? Бутерброды разные, падают при различных обстоятельствах, с разной высоты… Параметров столько, что говорить о закономерностях в такой задаче, наверное, нет смысла. Всяко бывает. Бывает, что падает маслом вниз, тогда становится обидно, мы вспоминаем про закон и запоминаем его. А если бутерброд падает неинтересно — маслом кверху, или если он оказался без масла вовсе, так и говорить не о чем — понятно же, что закон-то шуточный! В конце концов, бутерброд подобен монетке, которую математики используют для получения случайных величин с двумя возможными значениями: «орёл» и «решка». Если монетка «честная», то ей абсолютно неважно какой стороной падать, и мы говорим, что вероятность падения орла и решки одинаковы и равны . По идее, с бутербродами дела должны обстоять также. Мы вернёмся к ним в следующей главе, а пока присмотримся к самой, наверное, простой вероятностной системе — к монетке.

Монетку в теоретиковероятностных экспериментах подбрасывают каким-то особым магическим образом, так чтобы выбор начального положения, начальной скорости и скорости закручивания при подбрасывании никак не влиял на вероятность конкретного исхода. Но очевидно же, что это невозможно! Монетка представляет собой механическую систему и подчиняется законам механики, а они не содержат в себе случайных величин. Будущее в законах движения такого простого тела как монетка однозначно определяется прошлым состоянием этого тела. Если монетку будет подбрасывать робот, или демон Лапласа — мифическое существо, обладающее полной информацией о координатах и скоростях любой механической системы, то при неизменных начальных данных будут получаться идентичные результаты. Мы, конечно, не роботы и не демоны, но неужели люди подбрасывают монетки настолько неряшливо и непредсказуемо, что законы механики могут приводить к случайностям?

А откуда, вообще, берётся случайность в мире, описываемом законами механики? Откуда вообще, берётся случайность? В чём разница между истинно хаотическими или стохастическими системами, принципиально непредсказуемыми, и системами, в которых просто трудно угадать поведение, но его можно рассчитать?

Задача о монетке рассматривалась в 1986 году Джозефом Келлером. Мы приведём простое объяснение возникновению неопределённости в этом процессе, основанное на рассуждениях из статьи Келлера. То какой стороной упадёт монетка, зависит от времени её полёта и от угловой скорости . Если измерять угловую скорость в оборотах за единицу времени, то число оборотов, совершаемое монеткой, выражается предельно просто . Эта зависимость задаёт линии равного числа оборотов в координатах , а они, в свою очередь, ограничивают области, соответствующие чётному и нечётному числу оборотов.

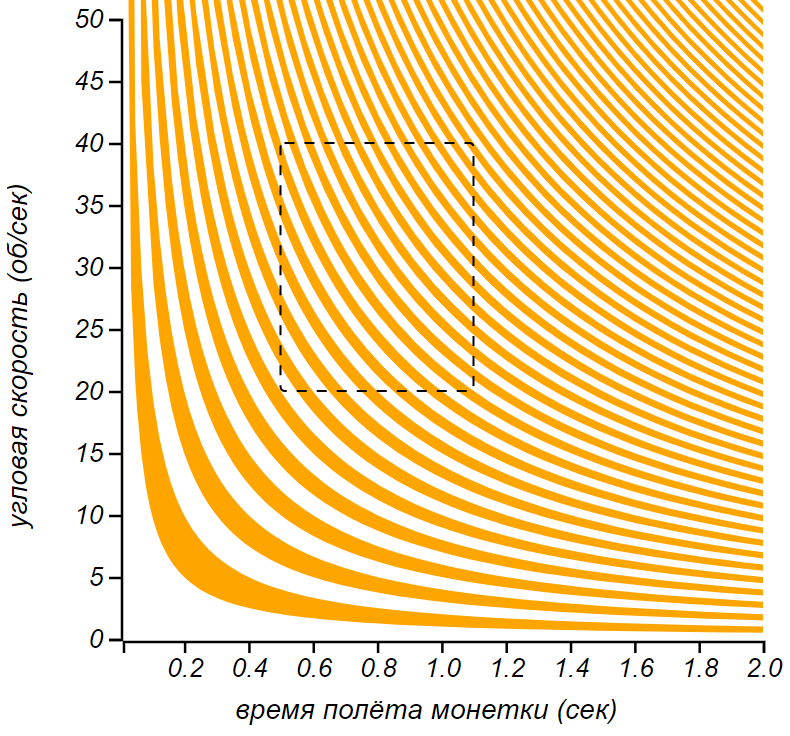
Диаграмма, показывающая чётность количества оборотов, совершаемых монеткой в полёте. Прямоугольником показана область, в которой чаще всего происходит процесс гадания на монетке.

На такой диаграмме можно показать каким будет результат подбрасывания монетки, закрученной на известное число оборотов в секунду, и пойманной через известное время подбрасывания. Если попадаем в белую полоску, то выпадет та же сторона, что была сверху при подбрасывании, если в оранжевую — обратная. Линии равного числа оборотов представляют собой гиперболы и видно, что по мере увеличения числа оборотов, чередование областей становится всё более и более частым, а сами области становятся тоньше. Человеческая рука несовершенна и очень небольшой разброс начальных значений перекрывает сразу много областей, делая исход непредсказуемым. В диапазоне действия руки (прямоугольник на диаграмме) достаточно смещения на  чтобы перескочить с белой полоски на оранжевую. Остаётся вопрос:, а как из этого построения следует «честность» настоящей механической монеты? Как из полученной диаграммы получить вероятность выпадения орла или решки?

Срочно примите меру!

Окунёмся немного в такую математику, которую не проходят в школе, чтобы лучше понять о чём мы рассуждаем. Мы говорили во введении, что математики изучают не числа или геометрические фигуры, как может показаться после изучения школьного курса. Они работают с математическими структурами (абстрактными алгебрами, полукольцами, полями, моноидами, топологическими пространствами и прочей абстрактной всячиной), описывают их, как кажется, совершенно не привязываясь к практике, определяют их, изучают их свойства, доказывают теоремы. А потом оттачивают мастерство в поиске подобных структур в самых различных областях знаний, совершая удивительно полезные прорывы, в том числе, в чисто прикладных отраслях. Мы сейчас немного коснёмся такой математики и рассмотрим как строится базис теории вероятностей, основанный на весьма абстрактном понятии меры.

Мы описали механику монетки и получили области, описывающие множества решений с определённым свойствами. Области — это плоские фигуры, как правильно перейти от них к вероятностям? Нам нужно измерять наши области и мы естественным образом приходим к их площади. Площадь — является мерой плоской фигуры. Это точный математический термин, обозначающий функцию, ставящую в соответствие множеству некую неотрицательную числовую величину. Примерами мер являются количества в перечислимых множествах (количество яблок в мешке, например), а также длины, площади, объёмы фигур.

В математике существует целый раздел, который называется теорий мер. Эта теория родилась на рубеже IXX — XX веков (у её истоков стояли Эмиль Борель и Анри Лебег) и открыла математикам широкие возможности для анализа очень сложно устроенных объектов: канторовых и фрактальных множеств. Она легла в основу функционального анализа и современной теории вероятностей, фундамент которой был заложен замечательным русским математиком Андреем Колмогоровым. Определение вероятности, как меры, позволяет увидеть все основные свойства вероятности как для дискретных, так и для непрерывных множеств.

Хотя наша книжка не учебник, но на этом стоит немного остановиться, чтобы взглянуть на понятия тории вероятностей как бы с «высоты птичьего полёта» и почувствовать вкус математики. Для начала, перечислим основные свойства любых мер. Для того, чтобы лучше себе их представить, можно использовать вместо слова «мера» слова «количество» или «длина» либо «площадь».

1. Мера пустого множества равна нулю.
2. Мера всего измеримого множества конечна для конечных мер.
3. Мера подмножества не превышает меры множества
4. Мера объединения двух произвольных множеств равна сумме мер этих множеств за вычетом меры их пересечения (аддитивность).
5. Мера дополнения подмножества равна разности мер всего множества и меры подмножества.

Всякая ли неотрицательная числовая функция может быть мерой? Вовсе нет. Например, возраст ставит человеку в соответствие вполне определённое число. Но возраст двух людей нельзя определить, как сумму их возрастов. И скорость бега не является мерой — два человека бегут не в два раза быстрее. А вот импульс (количество движения) или энергия уже обладают свойствами меры. Вес, количество денег, объём знаний, громкость крика хоть и не всегда легко измеримые вещи, но тоже могут служить мерой на множестве людей.

На интуитивном уровне с понятием вероятности знакомы сейчас, практически, все. Её оценивают политологи и журналисты на ток-шоу, её обсуждают говоря о глобальном потеплении или завтрашнем дожде, про неё рассказывают анекдоты: Какова вероятность встретить на Тверской динозавра? — Одна вторая: либо встречу, либо нет. В современной математике понятие вероятность определяется, как мера на особом множестве, которое называется вероятностное пространство. Оно включает в себя как элементарные события, так и их комбинации, получаемые с помощью операций объединения, пересечения и исключения. Пример элементарного события: «выпадение тройки при бросании кости». Пример события, не являющегося элементарным: «выпадение любого чётного числа кроме двойки». Итак, перечислим свойства вероятности:

1. Вероятность невозможного события равна нулю.
2. Вероятность для всего вероятностного пространства равна единице.
3. Если одно событие влечёт за собой другое, то вероятность второго не превышает вероятности первого. Отношение «влечёт за собой» для событий эквивалентно «является подмножеством» для множеств.
4. Вероятность наступления хотя бы одного из двух произвольных событий равна сумме вероятностей каждого их этих событий, минус вероятность того, что события случатся одновременно.
5. Вероятность ненаступления события равна один минус вероятность наступления события.

Присмотритесь к свойствам мер и вероятностей и станет видно, что мы говорим об одних и тех же свойствах.

Не все свойства вероятности вытекают из её определения, как меры: понятия независимости событий и способ вычисления вероятности одновременно двух или нескольких независимых событий как произведения из вероятностей вводятся через условную вероятность, но эти понятия согласуются с колмогоровским определением.

Дискретным случайным величинам соответствуют конечные счётные множества, в них естественной мерой является обыкновенный подсчёт количества элементов. Соответственно, вероятностью в дискретном вероятностном пространстве служит комбинаторный подсчёт вариантов, знакомый каждому студенту. Для непрерывных случайных величин, вероятность, как мера, больше похожа на длину или на площадь и тут мы говорим о плотностях вероятности.

Аналогия вероятности с мерой на этом не заканчиваются. Что такое среднее значение? Это аналог положения центра масс фигуры, состоящей из точечных масс или сплошного тела с известной плотностью. И вычисляются эти величины одинаково. А как характеризуется разброс случайных величин вокруг среднего: дисперсия? Также как момент инерции характеризует распределение массы вокруг центра масс. И опять, формулы вычисления дисперсии для выборки или распределения совпадают с формулами для момента инерции набора тел или твёрдого тела хитрой формы.

Кстати, если заменить в определениях и свойствах вероятности сумму на «максимум», а произведение на «минимум», то можно построить альтернативную теорию, она называется теорией возможностей. Так работает математика. Начинаем с абстрактных рассуждений: числа образуют алгебру с операциями сложения и умножения, но на ограниченном числовом интервале можно построить подобную алгебру с операциями минимум и максимум. Строим понятие меры на новой алгебре и выясняем, что она открывает новый взгляд на мир! В отличие от теории вероятностей в такой теории можно построить две согласованные меры — возможность и необходимость, причём они, в отличие от вероятности, хорошо согласуются как с операциями объединения, так и пересечения событий. Это направление созданное американцем Лотфи Заде, азербайджанцем по происхождению, служит основанием для нечёткой логики и используется в системах автоматического распознавания образов и принятия решений.

Невероятно, но факт!

Первое свойство мер кажется тривиальным, но оно интересно своей несимметричностью. Если мера подмножества равна нулю, это не значит, что оно пусто! Например, линия — это подмножество точек плоскости, но её площадь (мера) равна нулю. Бывают и более экзотичные примеры — канторовы и фрактальные множества, имеющие сложную структуру, содержащие бесконечное число точек, зримо «занимающие» некоторую площадь или объём, но тем не менее, имеющие нулевую меру.

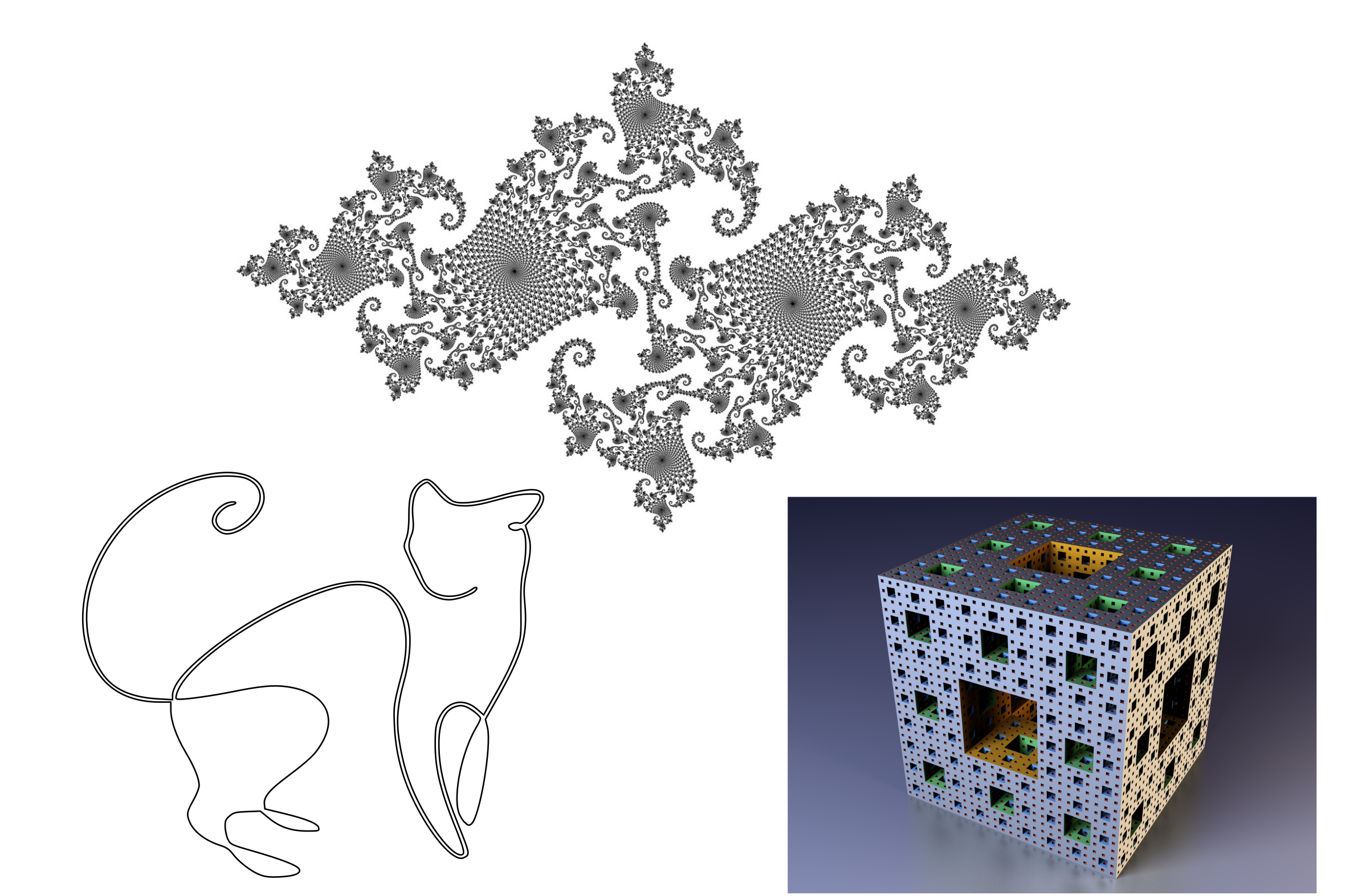Некоторые объекты нулевой меры: линия на плоскости, спорадическое множество Жулиа, фрактальная губка Менгера.

Готовя эту иллюстрацию, я отыскал замечательное изображение несвязного множества Жулиа на прозрачном фоне с высоким разрешением. Вставив его в векторный редактор, я столкнулся с забавной трудностью — было очень нелегко попасть мышкой в это изображение, чтобы выделить его. Оно такое «рыхлое», что вероятность попадания в закрашенный пиксел была заметно меньше попадания в прозрачный фон. В вероятностном пространстве тоже могут существовать подмножества нулевой меры, но это не означает, что события из этих подмножеств невозможны. С четвёртой-пятой попытки я всё же мог выделить изображение, поскольку пиксели имеют конечный размер. Но что было бы, попади в моё распоряжение настоящее несвязное множество Жулиа с бесконечным разрешением?

Представьте себе, что вы пользуетесь программным генератором случайных чисел, который выдаёт произвольное вещественное число от  до . Какова вероятность выпадения числа ?, а числа или ? Во всех этих случаях ответ будет — ноль! Вернее, самое маленькое доступное компьютеру положительное число, так называемый машинный эпсилон, ведь компьютер оперирует конечным числом знаков после запятой. Подождите, скажете вы, в каком смысле — ноль? Эти же числа не являются невозможными. Давайте проведём эксперимент, в результате мы получим какое-то конкретное число и когда мы его получим, то «по построению» вероятность его появления не может быть нулевой. Всё верно, но сколько нужно ждать до тех пор, пока не выпадет ровно 0? Практически бесконечно! Дело в том, что отдельное число, как точка на отрезке, имеет нулевую меру и честную нулевую вероятность. Отлична от нуля лишь мера сплошного отрезка, пусть даже очень маленького. Так что мы говорим не о вероятности, а о плотности вероятности, которая при умножении на конечную меру подмножества в вероятностном пространстве, даст конечную величину — вероятность попасть в это подмножество. Кстати, окажись у нас идеальный генератор случайных чисел с бесконечной точностью, вероятность получить с его помощью любое рациональное число тоже будет равна нулю.

Если кто-то терпеливо проведёт тысячу экспериментов с монеткой и радостно скажет вам, что у него получилось столько же выпадений «орлов», сколько и «решек», можете смело выразить сомнение, либо поздравить его с редкой удачей. Хоть бросание монетки и дискретный случайный процесс, но по мере накопления статистики мощность вероятностного пространства будет расти и мера события: «число «орлов» совпадает с числом «решек» будет уменьшаться. Можно показать, воспользовавшись формулой Стирлинга, что вероятность этого «самого вероятного» события стремится с ростом числа испытаний к нулю как . Для сотни бросаний это чуть больше пяти процентов, для десяти тысяч — всего полпроцента. В таких случаях математики говорят: почти наверняка количество «орлов» не будет равно количеству «решек». Как бы странно он не звучал, но «почти наверняка» — это точный математический термин, означающий что событие является дополнением подмножества вероятностного пространства нулевой меры. Мы ещё вернёмся к этим рассуждениям, в одной из следующих глав, когда зададимся вопросом: насколько каждый из нас может считать себя нормальным.

Проверяем честность реальной монеты

Вернёмся к монетке и к её честности. Колмогоровское определение вероятности примирило её частотное определение (как относительной частоты случающихся событий) и геометрическое (как доли «объёма» события в общем «объёме» возможностей). Таким образом, доля площади белых полосок на диаграмме рассчитанной для вращающейся монетки отражает вероятность выпадения той же стороны, которой мы её подкинули.

Но вот беда! Площадь каждой полоски на нашей диаграмме бесконечна (если рассматривать всю четверть координатной плоскости). Однако, аддитивность меры позволит нам аккуратно показать, что это не мешает площадям заштрихованных и белых областей быть одинаковыми. В явном виде уравнения для наших кривых имеют вид . Если площадь под кривой равна , то благодаря свойству аддитивности, площадь под кривой будет равна . В свою очередь, для отдельных полосок получаем: . Выходит, разница площадей не зависит от «номера» гиперболы. Это не что-то особенное, относящееся к гиперболам, тот же вывод можно сделать для любой кривой вида , лишь бы функция была измерима. А раз так, то для всей области определения, попадания в белую часть диаграммы или в заштрихованную равновероятны, как и ожидается для «честной» монетки.

Рассуждения, которые мы сейчас привели, кажутся достаточно простыми, но они дают весьма общий результат, применимый к любым аддитивным величинам. Абстрактное понятие меры позволило нам сравнивать между собой бесконечные величины, оставаясь в рамках логики и здравого смысла.

Абстракции это хорошо, но можно возразить, что в реальности мы подбрасываем монетки не со всеми возможными параметрами. Как показали эксперименты со скоростной камерой, угловые скорости попадают в диапазон от  до  оборотов в секунду, а длительность полёта — от половины до одной секунды. Эта область выделена прямоугольником на диаграмме. В ней суммарная площадь белых полосок чуть больше чем оранжевых, и можно сделать вывод, что вероятность выпадения той же стороны, что была при подбрасывании, составит .

В 2007 году группа Перси Диакониса с соавторами из Стэнфорда опубликовала статью, в которой даётся развёрнутый анализ процесса подбрасывания монетки. Детальное описание механики летящего и вращающегося диска, который, не просто вращается, а ещё и прецессирует — ось вращения сама вращается в полёте, показывает, что при ручном подбрасывании из позиции «орел сверху», вероятность выпадения «орла» на одну сотую больше половины.

Много это или мало? Сколько нужно провести экспериментов, чтобы заметить такую разницу? По мере накопления экспериментальных данных, стандартная ошибка среднего, отражающая погрешность, с которой может быть вычислена средняя величина, уменьшается пропорционально квадратному корню из числа испытаний: , здесь  — стандартное отклонение для исследуемого распределения. В нашем случае, для распределения Бернулли с вероятностью , которое равно . Чтобы уверенно выделить отклонение среднего в одну сотую, это отклонение должно превышать стандартных отклонения. Таким образом, мы можем оценить число испытаний:

Столько раз нужно подбросить монетку, чтобы заметить механистическую предопределённость результата. Чтобы было понятнее, что имеется ввиду, приведу пример двухсот испытаний идеальной и слегка неидеальной «монеток», проводимых с целью вычислить вероятность выпадения, скажем, орла. Каждое испытание состоит в  «подбрасываниях». Слова «монетка» и «подбрасывание» взяты в кавычки, оттого, что на самом деле использовалась не физическая монетка, а генератор случайных чисел, подчиняющихся распределению Бернулли.

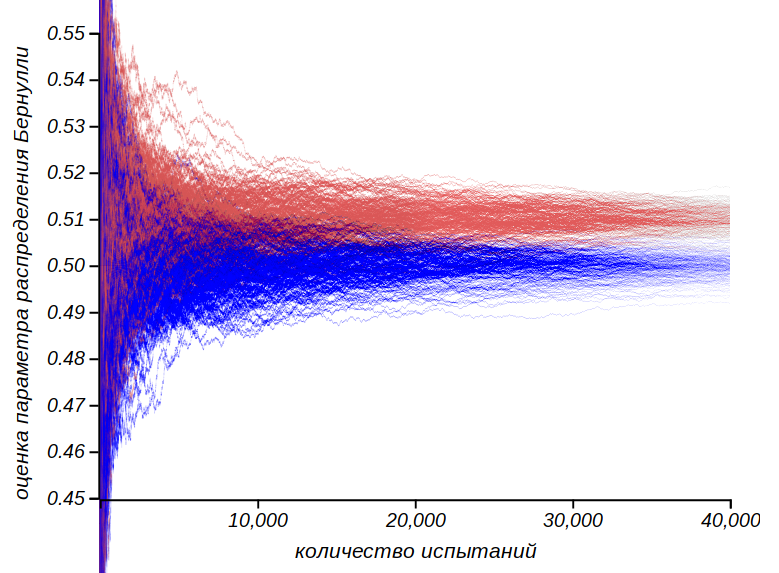
Эксперименты с подбрасыванием идеальной и слегка неидеальной монетки с целью зафиксировать неидеальность.

Видно, что только после испытаний «облака» наблюдаемых значений среднего начинают отчётливо разделяться. Что же, для бытового использования можно считать, что монетка — неплохой генератор случайного выбора из двух равновероятных вариантов.

Закон туриста

Эквивалентность геометрического и частотного определения вероятности раскрывает загадку одного закона подлости, известного в кругу туристов, геологов и всех тех, что пользуется топографическими картами:

То место, куда направляется турист, чаще всего оказывается либо на сгибе карты, либо на краю листа.

Предположим, что нас одинаково часто интересуют объекты, расположенные во всех участках карты. Но нас редко интересуют объекты нулевой меры — весь смысл использования карты состоит в обозрении окрестностей объекта, то есть некоторой конечной площади. Пусть нам достаточно будет некоторой малой доли от площади всей карты , чтобы разобраться в том, как попасть к объекту. Значит, если объект приблизится к сгибу или краю на какое-то критическое расстояние , мы сочтём закон туриста выполнившимся. Доля пограничных площадей в общем площади карты даст нам вероятность испытать этот закон подлости на себе. Вот как выглядят неприятные участки карты при  и одном сгибе.

Серым выделены «нехорошие» участки. Отдельно показан участок с полупроцентной площадью для карты шириной в 40 см, она имеет диаметр слегка превышающий 3 см.

Для квадратной карты . Неприятные полоски будут иметь площадь . Четыре полосы, две вертикальные и две горизонтальные, расположатся у края, любой дополнительный изгиб, горизонтальный или вертикальный, добавит ещё одну полоску. При этом пересекающиеся полоски добавляют лишние квадратики площадью . Сложив карту так, чтобы получилось горизонтальных и  вертикальных изгибов, мы получим суммарную площадь неприятной зоны равную: . Отнеся её к площади всей карты, получим неприятную долю общей площади:

На рисунке показаны области, в которых эта доля превышает для различных значений .

Области, в которых повышена вероятность оказаться на сгибе карты или на её краю. Числами отмечена доля площади рассматриваемой окрестности от площади всей карты.

Получается, что карта, сложенная пополам дважды уже может формально считаться нечестной по отношению к туристу. Чаще всего, карты имеют по три вертикальные и три горизонтальные складки, что даёт вероятность выполнения закона подлости с вероятностью около  при 

Откуда же берётся случайность?

В сувенирных лавках можно найти магнитные маятники для «выбора желаний». Они тоже являются механическими генераторами случайности и их иногда ошибочно называют «хаотическими маятниками». Начав движение с каких-то начальных позиции и скорости, маятник совершает ряд «непредсказуемых» колебаний и, наконец, останавливается в одном из секторов. Однако колебания и здесь не являются непредсказуемыми, просто они очень чувствительны к начальным условиям. Для каждого сектора, в котором может остановиться маятник, существует область притяжения в пространстве координат-скорости. Это множество таких начальных условий, при которых маятник обязательно притянется к определённой точке в указанном секторе. Точка остановки маятника называется аттрактором — притягивающей точкой. В случае маятника с картинки пространство координат и скоростей четырёхмерно, и так просто области притяжения не показать. Но если ограничиться лишь двумя секторами и свести задачу к одномерной (такой маятник называется осциллятором Дюффинга), то пространство начальных значений превратится в плоскость, так что области притяжения можно будет увидеть. Они выглядят как замысловатый символ «Инь-Янь», быстро превращающийся в узкие полоски, разделяющие области притяжения.

Области притяжения аттракторов для одномерного маятника желаний — осциллятора Дюффинга.

Как и в случае с монетой, немного смещая начальные условия мы попадаем от одного аттрактора к другому. Так же действует и игральная кость и рулетка, но они не являются сами по себе генераторами случайности. Это не истинно хаотические системы и их поведение можно точно рассчитать.

А что же такое настоящая случайность? Хороший пример истинно стохастической системы — появление автомобилей на дороге. Люди не договариваются, не согласовывают свои планы, каждый элемент ансамбля за пределами дороги действует независимо. И хотя в поведении людей есть определённые закономерности — часы пик утром и вечером, пустые дороги ночью и т.д., мы не обладаем и никогда не будем обладать достаточной информацией о каждом участнике движения, чтобы предсказать появление любого из них. Также стохастическими являются механика элементарных частиц на квантовом уровне, распад нестабильных атомов, изменения в генетическом коде, по всей видимости, землетрясения и котировки ценных бумаг на бирже. Единственное, что остаётся исследователю, это рассматривать их, как случайные величины и описывать в терминах теории вероятности.

Но есть и другой источник случайностей — динамический хаос. Хаотические системы отличаются от стохастических тем, что описываются точными уравнениями и параметрами, не содержащими случайностей. Однако их поведение не просто сложно, а хаотично и истинно непредсказуемо. Если мы начнём колебать маятник желаний, очень аккуратно, с точно контролируемой частотой и амплитудой, то мы обнаружим, что его плавные движения невозможно просчитать надолго. Никакими алгоритмами на сколь угодно точных вычислительных машинах нам не удастся рассчитать точное поведение маятника на произвольно далёкое будущее. Он не остановится на каком-либо секторе, а будет совершать плавные движения, но никогда не вернётся в одну и ту же точку в пространстве координат-скорости дважды. Ещё один пример предельно простой хаотической системы — идеальный шарик, подпрыгивающий в поле тяжести на идеальном столике с пружинкой. Сравнительно простые уравнения Лоренца показали, что мы никогда не сможем предсказывать погоду больше чем на пару-тройку недель — это тоже хаотическая система.

Теории динамического хаоса, удалось объяснить природу такой непредсказуемости. Простой одномерный маятник желаний, который мы рассматривали, имел две устойчивые стационарные точки — два аттрактора, и одну неустойчивую, от которой система старается уйти, она показана белым кружком. В хаотическом режиме вместо набора аттракторов в системе появляется бесконечное множество неустойчивых стационарных траекторий. Это множество бесконечно, но имеет нулевую меру, и представляет собой очень сложно устроенную несвязную структуру. Попав на одну таких траекторий, в принципе невозможно ей следовать, используя какие-либо конечные алгоритмы. Но самое удивительное, оказалось, что это бесконечное множество неустойчивых траекторий само по себе является притягивающим! 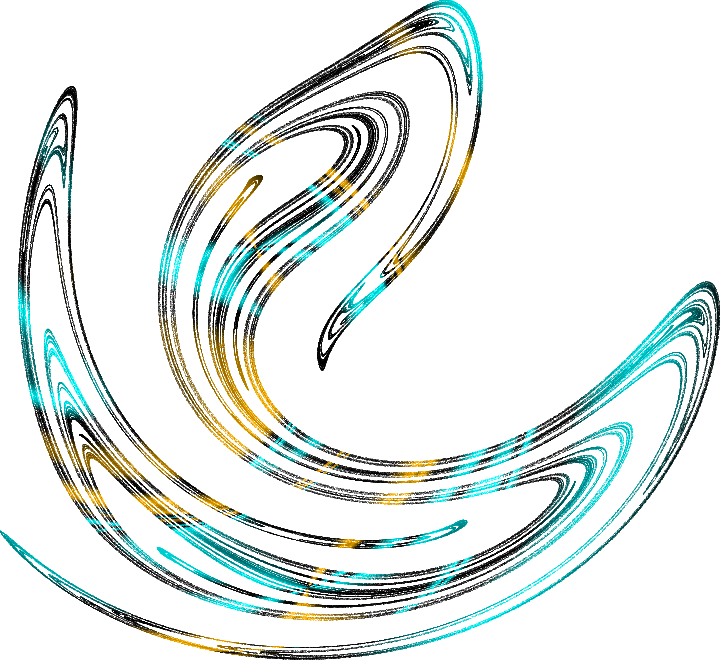Хаотическая система непрерывно перескакивает от окрестности одной неустойчивой траектории к другой, всё время оставаясь в пределах это странного аттрактора. Так эти множества и называются: странные аттракторы. Вот как завораживающе красиво выглядит сечение плоскостью странного аттрактора для маятника желаний, подверженного гармоническим колебаниям. Этот объект для одномерного маятника можно описать в трёхмерном пространстве (координата, скорость, фаза вынужденного колебания). Если рассечь аттрактор в этом пространстве плоскостью то можно увидеть его структуру, это называется сечением Пуанкаре. Каждая точка здесь — это след траектории, а цвет точек отражает относительную скорость с которой траектории разбегаются друг от друга. Вот ещё пара красивых странных аттракторов:

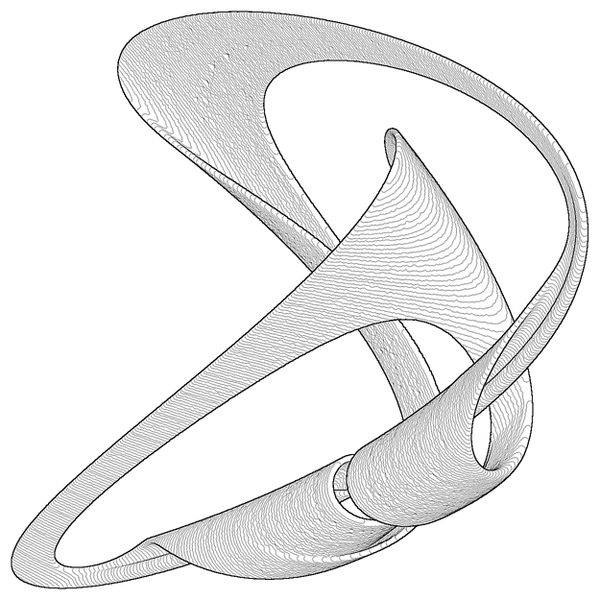
Слева: сечение Пуанкаре для траектории шарика, подпрыгивающего на подпружиненном столике. Множество точек принадлежит поверхности сферы, соответствующей закону сохранения энергии. Справа: объемная область, которая заключает в себе странный аттрактор, рождающийся при вынужденных колебаниях толстой пластины.

Гладкость хаотической траектории позволяет всё же немного заглядывать в будущее. Это объясняет одно досадное наблюдение: с одной стороны, синоптики, порой, не могут уверенно предсказать погоду на неделю, но с другой, если вы скажете, что завтра будет такая же погода, как и сегодня, то не ошибётесь примерно в трёх случаях из четырёх. Вообще же, анекдоты о синоптиках несправедливы и нужно отдать должное человеческой мысли и упорству, которые позволили предсказывать погоду на современном уровне!

Динамический хаос очень сложен и красив как теория, он порождает изумительные по элегантности образы, но он может быть ещё и полезен. Например, алгоритмы, с помощью которых генерируются случайные числа в компьютерах тоже детерминированы. Для примеров в этой книге, я пользовался генератором псевдослучайных чисел, который не запускал реальный стохастический процесс (альфа-распад, или подсчёт машин на дороге), а вычислял следующее «случайное» число на базе предыдущих, полученных им ранее.

От монеток к бабочкам и самой судьбе

Наблюдения за тем, как малые отклонения вырастают в глобальные изменения системы, приводят к мысли об «эффект

© Habrahabr.ru