Сжатие изображений без потерь
Как я уже обещал постом ранее, представляю вашему вниманию вторую часть большого рассказа о сжатии изображений. На этот раз речь пойдёт о методах сжатия изображений без потерь.Метод кодирования длин серийНаиболее простым для понимания алгоритмом является разработанный в 1950-х годах алгоритм кодирования длин серий. Основная идея алгоритма заключается в представлении каждой строки бинарного изображения в виде последовательности длин непрерывных групп чёрных и белых пикселей. Например, вторая строка изображения, приведённого на Рис. 1, будет выглядеть следующим образом: 2,3,2. Но в процессе декодирования возникнет неоднозначность, т.к. непонятно, какую серию: чёрную или белую кодирует первое число. Для решения этой проблемы существует два очевидных метода: либо для каждой строки предварительно указывать значение первого пиксела, либо договориться, что для каждой строки сначала указывается длина последовательности белых пикселов (при этом она может быть равна нулю).
Метод кодирования длин серий весьма эффективен, особенно для изображений с простой структурой, но этот метод может быть значительно улучшен, если дополнительно сжимать полученные последовательности каким-нибудь энтропийным алгоритмом, например, методом Хаффмана. Кроме того, энтропийный алгоритм может независимо применяться отдельно для чёрных и белых последовательностей, что ещё сильнее увеличит степень сжатия.Метод кодирования контуров
Дальнейшим развитием идеи кодирования длин серий является метод сжатия с отслеживания контуров. Этот метод основан на использовании высокоуровневых свойств сжимаемого изображения. Т.е. изображение воспринимается не просто как набор пикселов, а как объекты переднего плана и фон. Сжатие выполняется за счёт эффективного представления объектов. Существуют различные способы представления, которые мы рассмотрим далее на примере Рис. 2.
Прежде всего надо отметить, что описание каждого объекта должно быть заключено в специальные сообщения (теги) начала и конца объекта. Первый и самый простой способ — указывать координаты начальной и конечной точки контура на каждой строке. Изображение на Рис. 2 будет закодировано следующим образом:
<НАЧАЛО> СТР. 2 4–8 СТР. 3 3–8 СТР. 4 3–8<КОНЕЦ><НАЧАЛО> СТР. 6 2–8 СТР. 7 2–9 СТР. 8 2–9 СТР. 9 2–9<КОНЕЦ>
Разумеется, эта запись в дальнейшем сжимается с помощью рассмотренных ранее алгоритмов. Но, опять же, данные можно преобразовать таким образом, чтобы повысить дальнейшую степень сжатия. Для этого применяется т.н. дельта кодирование: вместо записи непосредственных координат границ записывается их смещение относительно предыдущей строки. С использованием дельта-кодирования изображение на Рис. 2 будет закодировано следующим образом: <НАЧАЛО> СТР. 2 4,8 СТР. 3 -1,0 СТР. 4 0,0<КОНЕЦ><НАЧАЛО> СТР. 6 2,8 СТР. 7 0,1 СТР. 8 0,0 СТР. 9 0,0<КОНЕЦ>
Эффективность дельта кодирования объясняется тем, что значения смещений по модулю близки к нулю и при большом количестве объектов в их описании будет много нулевых и близких к нулю значений. Преобразованные таким образом данные будут гораздо лучше сжиматься энтропийными алгоритмами.Кодирование областей постоянства
Заканчивая разговор о сжатии двоичных изображений, необходимо упомянуть о ещё одном методе — кодировании областей постоянства. В этом методе изображение разбивается на прямоугольник n1*n2 пикселов. Все полученные прямоугольники делятся на три группы: полностью белые, полностью чёрные и смешанные. Самая распространённая категория кодируется однобитовым кодовым словом, а остальные две категории получают коды из двух бит. При этом код смешанной области служит меткой, после которой идёт n1*n2 бит, описывающих прямоугольник. Если разбить хорошо известное изображение с Рис. 2 на квадраты 2×2 пиксела, то получится пять белых квадратов, шесть чёрных и 13 смешанных. Договоримся 0 обозначать метку смешанного квадрата, 11 — метку белого квадрата, а 10 — метку чёрного квадрата, единичный белый пиксел будем кодировать 1, а чёрный, соответственно, 0. Тогда всё изображение будет закодировано следующим образом (жирным выделены метки): 
Как и у большинства методов сжатия, эффективность этого метода тем выше, чем больше исходное изображение. Кроме того, можно заметить, что значения смешанных квадратов могут быть весьма эффективно сжаты словарными алгоритмами.На этом мы закончим рассказ о сжатии двоичных изображений и перейдём к рассказу о сжатии без потерь полноцветных и монохромных изображений.Существует множество различных подходов к сжатию изображений без потерь. Самые тривиальные сводятся к прямому применению алгоритмов, рассмотренных постом ранее, другие более совершенные алгоритмы используют информацию о типе сжимаемых данных.Кодирование битовых плоскостей
Первым способом, который мы рассмотрим, будет способ, известный как кодирование битовых плоскостей. Рассмотрим произвольное изображение с n уровнями яркости. Очевидно, что эти уровни могут быть представлены с помощью log2n бит. Метод разложения на битовые плоскости заключается в разделении одного изображения с n уровнями яркости на log2n бинарных изображений. При этом i-ое изображение получается путём выделения i-ых битов из каждого пиксела исходного изображения. В Табл. 1 показано разложение исходного изображения по битовым плоскостям.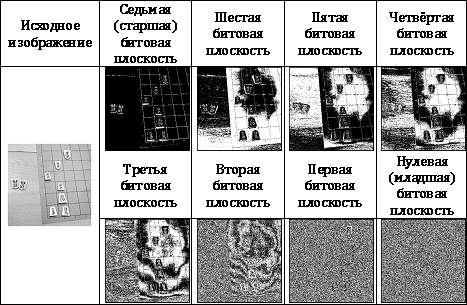
После разложения изображения на битовые плоскости каждое полученное изображение можно сжать, используя рассмотренные ранее методы сжатия двоичных изображений.Довольно очевидным недостатком данного подхода является эффект многократного переноса разрядов при незначительном изменении яркости. Например, при изменении яркости со 127 на 128 произойдёт изменение значений всех двоичных разрядов (0111111→10000000), что вызовет изменение всех битовых плоскостей.Чтобы снизить негативные последствия от многократных переносов, на практике часто используются специальные коды, например коды Грея, в которых два соседних элемента различаются только в одном разряде. Для перевода n-битного числа в код Грея необходимо выполнить операцию побитового исключающего ИЛИ с этим же числом, сдвинутым на один бит вправо. Обратное преобразование из кода Грея можно осуществить, выполняя побитовую операцию исключающего ИЛИ для всех сдвигов исходного числа, не равных нулю. Алгоритмы преобразования в код Грея и из него приведены в Листинг 1.
function BinToGray (BinValue: byte): byte; begin BinToGray := BinValue xor (BinValue shr 1); end; function GrayToBin (GrayValue: byte): byte; var BinValue: integer; begin BinValue := 0; while GrayValue > 0 do begin BinValue := BinValue xor GrayValue; GrayValue := GrayValue shr 1; end; GrayToBin := BinValue; end;
Легко убедиться, что после преобразования в код Грея при смене яркости со 127 на 128 меняется только один двоичный разряд: 
Битовые плоскости, полученные с помощью кода Грея, более монотонны и в общем случае лучше поддаются сжатию. В Табл. 2 показаны битовые плоскости, полученные из исходного изображения, и изображения, преобразованного в код Грея: 
Кодирование с предсказанием
В основе кодирования с предсказанием лежит идея, похожая на алгоритм дельта кодирования. Большинство реальных изображений локально однородны, т.е. соседи пиксела имеют примерно ту же яркость, что и сам пиксел. Это условие не выполняется на границах объектов, но для большей части изображения оно верно. Исходя из этого можно предсказать значение яркости пиксела, основываясь на яркости соседей. Разумеется, это предсказание не будет абсолютно точным, и будет возникать ошибка предсказания. Именно эта ошибка предсказания в дальнейшем кодируется с помощью энтропийных алгоритмов. Эффективность кодирования обеспечивается за счёт уже упомянутого свойства локальной однородности: на большей части изображения значение ошибки по модулю будет близко к нулю.При этом способе кодирования очень важно, чтобы и при кодировании, и при декодировании использовался один и тот же предсказатель. В общем случае предсказатель может использовать любые характеристики изображения, но на практике предсказанное значение чаще всего вычисляется как линейная комбинация яркостей соседей: pk=∑i=1Mαi*pk-i. В этой формуле M — число соседей, участвующих в предсказании (порядок предсказания), индексы p — номера пикселей в порядке их просмотра. Можно заметить, что при M=1 кодирование с предсказанием превращается в рассмотренное ранее дельта кодирование (правда, вместо разницы координат теперь кодируется разность яркостей).Тут необходимо немного обсудить порядок просмотра пикселей. До этого момента мы предполагали, что пикселы просматриваются слева направо и сверху вниз, т.е. в порядке обхода строками (Табл. 3):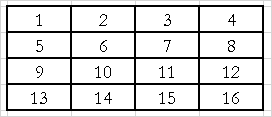 
Но очевидно, что результат предсказания яркости пятого пиксела на основе четвёртого (при обходе строками) будет очень далёк от истинного результата. Поэтому на практике часто используют другие порядки обхода, например, обход строками с разворотом, змейкой, полосами, полосами с разворотом, и т.д. Некоторые из перечисленных вариантов обхода приведены в Табл. 4
Рассмотрим описанный метод на конкретном примере. Попробуем применить кодирование с предсказанием для изображения Останкинской телебашни на Рис. 3
Для простоты будем использовать предсказание первого порядка (дельта кодирование) и обход по строкам (каждую строку будем кодировать независимо). При программной реализации необходимо решить, как передавать информацию о первых M пикселах, значение которых невозможно предсказать. В реализации Листинг 2 используется следующий подход: первый пиксел каждой строки кодируется непосредственно значением своей яркости, а все последующие пикселы в строке предсказываются на основе одного предыдущего.
type TPredictionEncodedImg = array of array of integer; function DeltaEncoding: TPredictionEncodedImg; var r: TPredictionEncodedImg; i, j: word; begin SetLength (r, GSI.N + 1); for i := 1 to GSI.N do begin SetLength (r[i], GSI.M + 1); r[i, 1] := GSI.i[i, 1]; end; for i := 1 to GSI.N do for j := 2 to GSI.M do r[i, j] := GSI.i[i, j] — GSI.i[i, j — 1]; DeltaEncoding := r; end;
В Табл. 5 представлен результат работы данного алгоритма. Белым цветом показаны пикселы, предсказанные точно, а ошибки отмечены цветом, причём положительное значение ошибки отображается красным цветом, а отрицательное — зелёным. Интенсивность цвета соответствует модулю величины ошибки.
Анализ показывает, что подобная реализация обеспечивает среднюю ошибку предсказания всего в 0.21 уровня яркости. Использование предсказаний более высокого порядка и других способов обхода позволяет ещё сильнее уменьшить ошибку предсказания, а значит, увеличить степень сжатия.
