Сверточная сеть на python. Часть 2. Вывод формул для обучения модели18.12.2017 14:03

В прошлой статье мы рассмотрели концептуально все слои и функции, из которых будет состоять будущая модель. Сегодня мы выведем формулы, которые будут отвечать за обучение этой модели. Слои будем разбирать в обратном порядке — начиная с функции потерь и заканчивая сверточным слоем. Если возникнут трудности с пониманием формул, рекомендую ознакомиться с подробным объяснением (на картинках) метода обратного распространения ошибки, и также вспомнить о правиле дифференцирования сложной функции.

Вывод формулы для обратного распространения ошибки через функцию потерь

Это просто частная производная функции потерь по выходу модели.

С производной в числителе обращаемся как с производной от сложной функции: . Здесь, кстати, видно, как сокращаются и , и становится понятно, зачем в формуле мы изначально добавили

Сначала я использовал среднеквадратическое отклонение, но для задачи классификации лучше применить cross-entropy (ссылка с объяснением). Ниже формула для backprop, попытался максимально подробно написать вывод формулы:

Помним, что 

Вывод формулы backprop через функции активации

… через ReLU

 — обозначение backprop через функцию активации.

То есть мы пропускаем ошибку через те элементы, которые были выбраны максимальными во время прямого прохождения через функцию активации (умножаем ошибку с предыдущих слоев на единицу), и не пропускаем для тех, которые не были выбраны и, соответственно, не повлияли на результат (умножаем ошибку с предыдущих слоев на ноль).

… через сигмоиду

Здесь нужно помнить, что 
При этом  — это формула сигмоиды

Далее обозначим как  (где )

… также через softmax (или здесь)

Эти расчеты показались мне немного сложнее, так как функция softmax для i-того выхода зависит не только от своего , но и от всех других , сумма которых лежит в знаменателе формулы для прямого прохожденя через сеть. Поэтому и формула для backprop «распадается» на две: частная производная по  и :

Применяем формулу где и 
При этом

И частная производная по :

Исходя из формулы выше, есть нюанс с тем, что должна возвращать функция (в коде) при обратном распространении ошибки для  при softmax, так как в этом случае для расчета одной используются все , или, другими словами, каждая влияет на все :

В случае softmax будет равен (появилась сумма!), то есть:

При этом значения для всех у нас есть, это backprop через лосс функцию. Осталось найти для всех и всех  — то есть это матрица. Ниже матричное умножение в «развернутом» виде, чтобы лучше было понятно, почему  — матрица и откуда появляется матричное умножение.

Речь шла как раз об этой последней в разложении матрице — . Посмотрите, как при перемножении матриц и  мы получаем . А значит, выходом функции backprop (в коде) для softmax должна быть матрица , при умножении на которую уже рассчитанного на тот момент , мы и получим .

Бэкпроп через полносвязную сеть

Вывод формулы backprop для обновления матрицы весов fc-сети

Раскладываем сумму в числителе и получаем, что все частные производные равны нулю, кроме случая , что равняется . Этот случай происходит, когда . Штрих здесь для обозначения «внутреннего» цикла по , то есть это совсем другой итератор, не связанный с  из 

И вот так это будет выглядеть матричном виде:

Размерность матрицы равна , и для того, чтобы произвести матричное умножение, матрицу следует транспонировать. Ниже привожу матрицы полностью, в «развернутом» виде, чтобы выкладки казались яснее.

Вывод формулы backprop для обновления матрицы

Для bias все вычисления очень схожи с предыдущим пунктом:

Понятно, что 

В матричном виде тоже все довольно просто:

Вывод формулы backprop через 

В формуле ниже сумма по  возникает от того, что каждый соединен с каждым (помним, что слой называется полносвязной)

Раскладываем числитель и видим, что все частные производные равны нулю, кроме того случая, когда :

И в матричном виде:

Далее матрицы в «раскрытом» виде. Замечу, что индексы самой последней матрицы я намеренно оставил в том виде, в каком они были до транспонирования, чтобы лучше было видно, какой элемент куда перешел после транспонирования.

Далее обозначаем как , и все формулы для обратного распространения ошибки через последующие слои полносвязной сети вычисляются аналогичным образом.

Бэкпроп через макспулинг

Ошибка «проходит» только через те значения исходной матрицы, которые были выбраны максимальными на шаге макспулинга. Остальные значения ошибки для матрицы будут равны нулю (что логично, ведь значения по этим элементам не были выбраны функцией макспулинга во время прямого прохождения через сеть и, соответственно, никак не повлияли на итоговый результат).

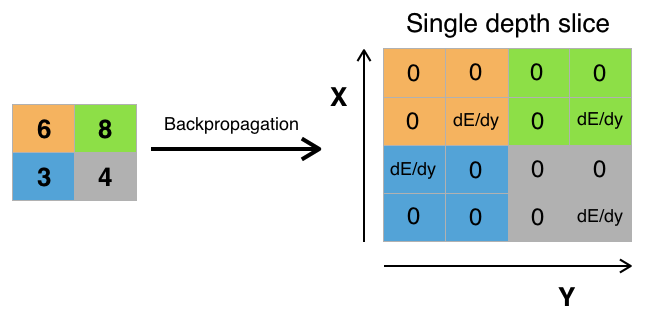
Вот реализация макспулинга на python:

import numpy as np

y_l = np.array([
	[1,0,2,3],
	[4,6,6,8],
	[3,1,1,0],
	[1,2,2,4]])

other_parameters={
	'convolution':False,
	'stride':2,
	'center_window':(0,0),
	'window_shape':(2,2)
}

def maxpool(y_l, conv_params):
	indexes_a, indexes_b = create_indexes(size_axis=conv_params['window_shape'], center_w_l=conv_params['center_window'])
	stride = conv_params['stride']
	# выходные матрицы будут расширяться по мере добавления новых элементов
	y_l_mp = np.zeros((1,1)) # матрица y_l после операции макспулинга
	y_l_mp_to_y_l = np.zeros((1,1), dtype='= 0 and j*stride - g*b >= 0 \
					and i*stride - g*a < y_l.shape[0] and j*stride - g*b < y_l.shape[1]:
						if y_l[i*stride - g*a][j*stride - g*b] > result:
							result = y_l[i*stride - g*a][j*stride - g*b]
							i_back = i*stride - g*a
							j_back = j*stride - g*b
						element_exists = True
			# запись полученных результатов только в том случае, если для данных i и j были произведены вычисления
			if element_exists:
				if i >= y_l_mp.shape[0]:
					# добавление строки, если не существует
					y_l_mp = np.vstack((y_l_mp, np.zeros(y_l_mp.shape[1])))
					# матрица y_l_mp_to_y_l расширяется соответственно матрице y_l_mp
					y_l_mp_to_y_l = np.vstack((y_l_mp_to_y_l, np.zeros(y_l_mp_to_y_l.shape[1])))
				if j >= y_l_mp.shape[1]:
					# добавление столбца, если не существует
					y_l_mp = np.hstack((y_l_mp, np.zeros((y_l_mp.shape[0],1))))
					y_l_mp_to_y_l = np.hstack((y_l_mp_to_y_l, np.zeros((y_l_mp_to_y_l.shape[0],1))))
				y_l_mp[i][j] = result
				# в матрице y_l_mp_to_y_l хранятся координаты значений,
				# которые соответствуют выбранным в операции максипулинга ячейкам из матрицы y_l
				y_l_mp_to_y_l[i][j] = str(i_back) + ',' + str(j_back)
	return y_l_mp, y_l_mp_to_y_l

def create_axis_indexes(size_axis, center_w_l):
	coordinates = []
	for i in range(-center_w_l, size_axis-center_w_l):
		coordinates.append(i)
	return coordinates

def create_indexes(size_axis, center_w_l):
	# расчет координат на осях ядра свертки в зависимости от номера центрального элемента ядра
	coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0])
	coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1])
	return coordinates_a, coordinates_b

out_maxpooling = maxpool(y_l, other_parameters)
print('выходная матрица:', '\n', out_maxpooling[0])
print('\n', 'матрица с координатами для backprop:', '\n', out_maxpooling[1])

Пример выхода работы скрипта

Вторая матрица, которую возвращает функция, и есть те координаты элементов, выбранных из исходной матрицы во время операции макспулинга.

Бэкпроп через сверточную сеть

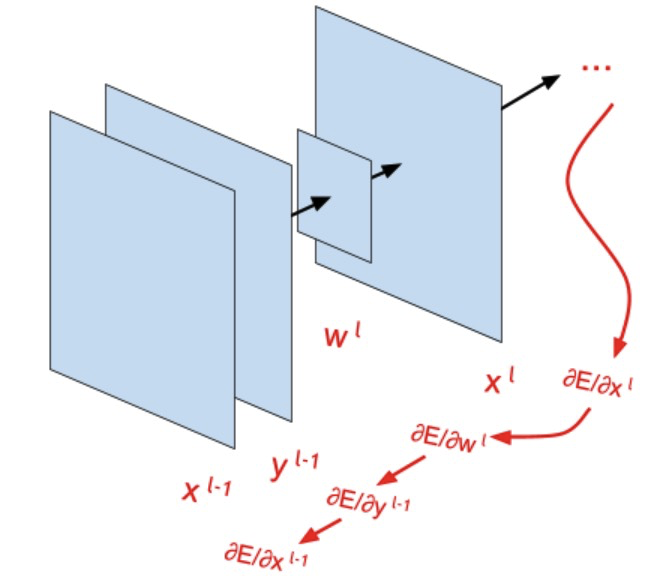
Вывод формулы backprop для обновления ядра свертки

(1) здесь просто подставляем формулу для , штрихи над  и  просто обозначают, что это другой итератор.
(2) здесь раскладываем сумму в числителе по  и :

то есть все частные производные в числителе, кроме тех, для которых которых , будут равны нулю. При этом равен

Все выше относится к конволюции. Формула backprop для кросс-корреляции выглядит аналогично, за исключением смены знака при  и :

Здесь важно увидеть, что в итоговой формуле не участвует само ядро свертки. Происходит некое подобие операции свертки, но с участием уже и , причем в роли ядра выступает , но все-таки это мало напоминает свертку, особенно при значении шага больше единицы: тогда «распадается» по , что совсем перестает напоминать привычную свертку. Этот «распад» происходит от того, что параметры и  итерируются внутри цикла формулы. Посмотреть, как все это выглядит, можно с помощью демонстрационного кода:

import numpy as np

w_l_shape = (2,2)

# если stride = 1
dEdx_l = np.array([
	[1,2,3,4],
	[5,6,7,8],
	[9,10,11,12],
	[13,14,15,16]])

# если stride = 2 и 'convolution':False (при конволюции и кросс-корреляци x_l получаются разного размера)
# dEdx_l = np.array([
# 	[1,2],
# 	[3,4]])

# если stride = 2 и 'convolution':True
# dEdx_l = np.array([
# 	[1,2,3],
# 	[4,5,6],
# 	[7,8,9]])

y_l_minus_1 = np.zeros((4,4))

other_parameters={
	'convolution':True,
	'stride':1,
	'center_w_l':(0,0)
}

def convolution_back_dEdw_l(y_l_minus_1, w_l_shape, dEdx_l, conv_params):
	indexes_a, indexes_b = create_indexes(size_axis=w_l_shape, center_w_l=conv_params['center_w_l'])
	stride = conv_params['stride']
	dEdw_l = np.zeros((w_l_shape[0], w_l_shape[1]))
	# в зависимости от типа операции меняется основная формула функции
	if conv_params['convolution']:
		g = 1 # операция конволюции
	else:
		g = -1 # операция корреляции
	# итерация по a и b ядра свертки
	for a in indexes_a:
		for b in indexes_b:
			# размерность матрицы для демонстрации конволюции равноа размерности y_l, так как эта матрица либо равна либо больше (в случае stride>1) матрицы x_l
			demo = np.zeros([y_l_minus_1.shape[0], y_l_minus_1.shape[1]])
			result = 0
			for i in range(dEdx_l.shape[0]):
				for j in range(dEdx_l.shape[1]):
					# проверка, чтобы значения индексов не выходили за границы
					if i*stride - g*a >= 0 and j*stride - g*b >= 0 \
					and i*stride - g*a < y_l_minus_1.shape[0] and j*stride - g*b < y_l_minus_1.shape[1]:
						result += y_l_minus_1[i*stride - g*a][j*stride - g*b] * dEdx_l[i][j]
						demo[i*stride - g*a][j*stride - g*b] = dEdx_l[i][j]
			dEdw_l[indexes_a.index(a)][indexes_b.index(b)] = result # перевод индексов в "нормальные" для извлечения элементов из матрицы w_l
			# вывод матрицы demo для отслеживания хода свертки
			print('a=' + str(a) + '; b=' + str(b) + '\n', demo)
	return dEdw_l

def create_axis_indexes(size_axis, center_w_l):
	coordinates = []
	for i in range(-center_w_l, size_axis-center_w_l):
		coordinates.append(i)
	return coordinates

def create_indexes(size_axis, center_w_l):
	# расчет координат на осях ядра свертки в зависимости от номера центрального элемента ядра
	coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0])
	coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1])
	return coordinates_a, coordinates_b

print(convolution_back_dEdw_l(y_l_minus_1, w_l_shape, dEdx_l, other_parameters))

Пример выхода работы скрипта

Вывод формулы backprop для обновления весов bias

Аналогично предыдущему пункту, только заменяем на . Будем использовать один bias для одной карты признаков:

то есть, если разложить сумму по всем и , мы увидим, что все частные производные по  будут равны единице:

Для одной карты признаков всего один bias, который «связан» со всеми элементами этой карты. Соответственно, при корректировке значения bias должны учитываться все значения из карты, полученные при обратном распространении ошибки. В качества альтернативного варианта можно брать столько bias для отдельной карты признаков, сколько элементов находится в этой карте, но в таком случае параметров bias будем слишком много — больше, чем параметров самих ядер свертки. Для второго случая также легко посчитать производную — тогда каждая (обратите внимание, у bias уже появились подстрочные индексы ) будет равна каждой .

Вывод формулы backprop через слой конволюции

Здесь все аналогично предыдущим выводам:

Раскладывая сумму в числителе по  и , получим, что все частные производные равны нулю, кроме того случая, когда и , и, соответственно, , . Это справедливо только для конволюции, для кросс-корреляции должно быть и  и, соответственно, и . И тогда итоговая формула в случае кросс-корреляции будет выглядеть так:

Получившиеся выражения — это та же самая операция свертки, причем в качестве ядра выступает знакомое нам ядро . Но, правда, все похоже на привычную свертку только если stride равен единице, в случаях же другого шага, получается уже что-то совсем другое (аналогично случаю backprop для обновления ядра свертки): матрица начинает «ломаться» по всей матрице , захватывая разные ее части (опять-таки потому, что индексы и  при  итерируются внутри цикла формулы).

Здесь можно посмотреть и потестировать код:

import numpy as np

w_l = np.array([
	[1,2],
	[3,4]])

# если stride = 1
dEdx_l = np.zeros((3,3))

# если stride = 2 и 'convolution':False (при конволюции и кросс-корреляци x_l могут получиться разного размера)
# dEdx_l = np.zeros((2,2))

# если stride = 2 и 'convolution':True
# dEdx_l = np.zeros((2,2))

y_l_minus_1_shape = (3,3)

other_parameters={
	'convolution':True,
	'stride':1,
	'center_w_l':(0,0)
}

def convolution_back_dEdy_l_minus_1(dEdx_l, w_l, y_l_minus_1_shape, conv_params):
	indexes_a, indexes_b = create_indexes(size_axis=w_l.shape, center_w_l=conv_params['center_w_l'])
	stride = conv_params['stride']
	dEdy_l_minus_1 = np.zeros((y_l_minus_1_shape[0], y_l_minus_1_shape[1]))
	# в зависимости от типа операции меняется основная формула функции
	if conv_params['convolution']:
		g = 1 # операция конволюции
	else:
		g = -1 # операция корреляции
	for i in range(dEdy_l_minus_1.shape[0]):
		for j in range(dEdy_l_minus_1.shape[1]):
			result = 0
			# матрица для демонстрации конволюции
			demo = np.zeros([dEdx_l.shape[0], dEdx_l.shape[1]])
			for i_x_l in range(dEdx_l.shape[0]):
				for j_x_l in range(dEdx_l.shape[1]):
					# перевод индексов в "нормальные" для извлечения элементов из матрицы w_l
					a = g*i_x_l*stride - g*i
					b = g*j_x_l*stride - g*j
					# проверка на вхождение в диапазон индексов ядра свертки
					if a in indexes_a and b in indexes_b:
						a = indexes_a.index(a)
						b = indexes_b.index(b)
						result += dEdx_l[i_x_l][j_x_l] * w_l[a][b]
						demo[i_x_l][j_x_l] = w_l[a][b]
			dEdy_l_minus_1[i][j] = result
			# вывод матрицы demo для отслеживания хода свертки
			print('i=' + str(i) + '; j=' + str(j) + '\n', demo)
	return dEdy_l_minus_1

def create_axis_indexes(size_axis, center_w_l):
	coordinates = []
	for i in range(-center_w_l, size_axis-center_w_l):
		coordinates.append(i)
	return coordinates

def create_indexes(size_axis, center_w_l):
	# расчет координат на осях ядра свертки в зависимости от номера центрального элемента ядра
	coordinates_a = create_axis_indexes(size_axis=size_axis[0], center_w_l=center_w_l[0])
	coordinates_b = create_axis_indexes(size_axis=size_axis[1], center_w_l=center_w_l[1])
	return coordinates_a, coordinates_b

print(convolution_back_dEdy_l_minus_1(dEdx_l, w_l, y_l_minus_1_shape, other_parameters))

Пример выхода работы скрипта

Интересно, что если мы выполняем кросс-корреляцию, то на этапе прямого прохождения через сеть мы не переворачиваем ядро свертки, но переворачиваем его при обратном распространении ошибки при прохождении через слой свертки. Если же применяем формулу конволюции — все происходит ровно наоборот.

В этой статье мы вывели и подробно рассмотрели все формулы обратного распространения ошибки, то есть формулы, позволяющие будущей модели обучаться. В следующей статье мы соединим все это в один цельный код, который и будет называться сверточной сетью, и попробуем эту сеть обучить предсказывать классы на настоящем датасете. А также проверим, насколько все вычисления корректны в сравнении с библиотекой для машинного обучения tensorflow.

© Habrahabr.ru