Сверхлёгкие частицы размером с галактику

Расправившись со статьёй про «волны-убийцы», я ещё некоторое время по инерции запускал описанную там модель с различными начальными условиями. На каком-то этапе пришла мысль обобщить код на большие измерения и произвести расчёт для поля, заполненного случайными возмущениями. Результат крайне озадачил и увёл меня в совсем другое направление, заставив на несколько месяцев погрузиться в космологию и физику тёмной материи.
Это четвёртая статья из цикла, посвящённого солитонике нелинейного уравнения Шрёдингера. Предыдущие работы:
В двух словах: при решении нелинейного уравнения Шрёдингера методом Фурье с разделённым шагом мы получали солитонные решения — уединённые волны, самопроизвольно возникающие благодаря модуляционной нестабильности и сохраняющие форму длительное время. Но что, если в качестве начальных условий взять приподнятый фронт, покрытый мелкой рябью — гауссовым шумом, а потом подождать, пока он не устаканится?
# начальная волновая функция, кол-во кадров в анимации, кол-во шагов между кадрами
function nlse_ssft!( ψ, timelayers, timesteps;
dt = 0.05, α = 0.5, σ = 1.0, xsteps = 128, xbox = (-10, 10) )
# шаг по времени, дисперсия, нелинейность,
# количество элементов в массиве вдоль одного измерения, границы в пространстве
Nd = ndims(ψ) # мерность задачи
Nx = size(ψ,1)
X = range(xbox[1], length = Nx, stop=xbox[2])
T = range(dt*timesteps, length = timelayers, step = dt*timesteps)
dx = step(X)
xcut = Nx ÷ xsteps # на выходе не весь тяжёлый массив
xscaled = [xcut:xcut:Nx for _ in 1:Nd]
Psi = Array{ComplexF64, Nd}[]
p = im*dt*σ
K = fftfreq(Nx) * (2π/dx)
k² = [ sum(i-> K[i]^2, Tuple(i) ) for i in CartesianIndices(size(ψ)) ]
eᵏ = exp.(-im*α*dt*k²)
for i in 1:timelayers
for _ = 1:timesteps
ψ .*= exp.( p*abs2.(ψ) )
fft!(ψ)
ψ .*= eᵏ
ifft!(ψ)
end
push!(Psi, ψ[xscaled...])
end
return X[xscaled[1]], T, Psi
end;
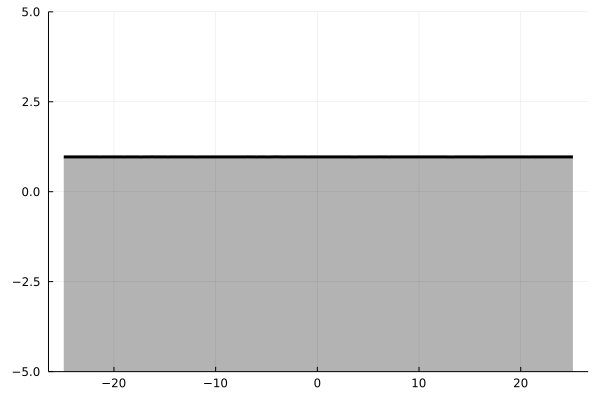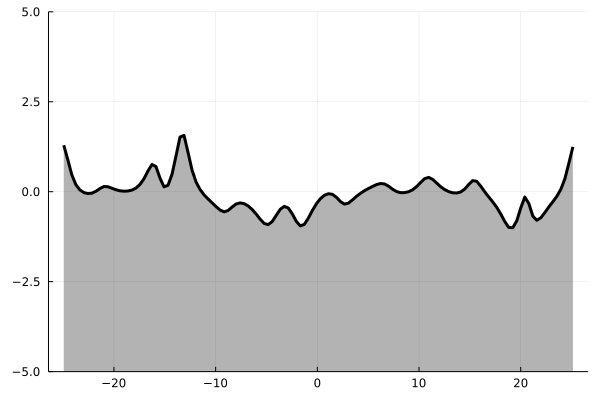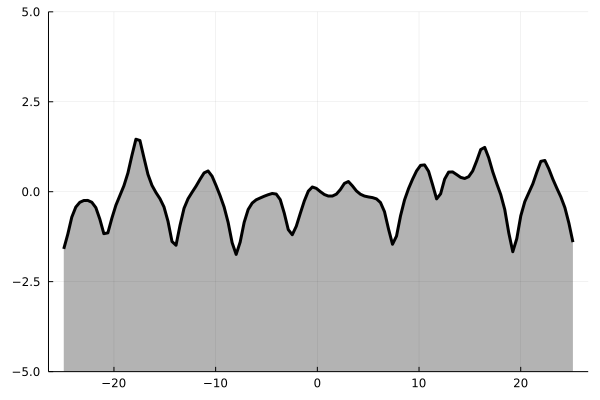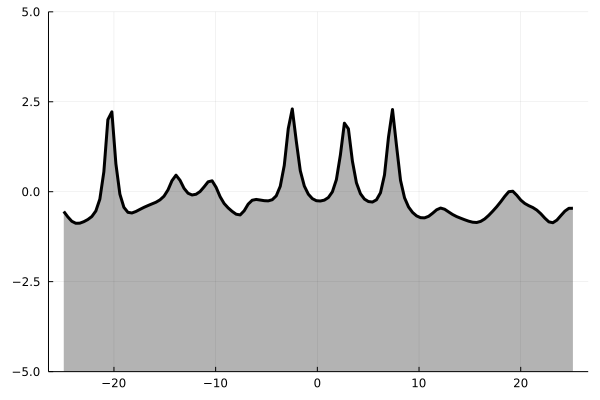
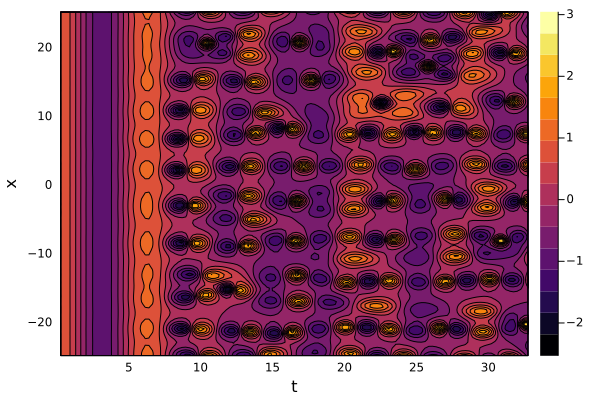
Появляются уединённые стоячие волны — бризеры. Но эксперимент можно повторить для двух- или трёхмерной области:

В обоих случаях возмущения филаментируются — образуют нитеподобные структуры, которые затем обрываются, скапливаются в сгустки и в конце концов вырождаются в сингулярности. В принципе такое поведение решения нелинейного уравнения Шрёдингера не должно вызывать удивления: например, оно находит применение в описании самофокусирующихся лазерных лучей-филаментов. Но ещё эта картинка напоминает (помимо складок на поверхности мозга) типичные изображения крупномасштабных структур Вселенной, которые каким-то образом связаны с тёмной материей. Что же, пришло время как следует погрузиться в эту тему.
Спектры
Starlight
I will be chasing the starlight
Until the end of my life
I don’t know if it’s worth it anymore
Muse
На младших курсах я ещё застал те времена, когда на технические специальности нашего провинциального вуза поступала увлечённая молодёжь, а не хвост рейтинга результатов ЕГЭ из-за низких проходных баллов. В общежитии бушевала безалаберная романтика юности и интеллекта: страстные умы жадно кидались на любую проблему, зачастую раздувая её из обыденных явлений, и схлёстывались в нескончаемых спорах. У обилия энтузиастов разных специальностей всегда можно было научиться чему-то новому: филологи расскажут про языки, радикально отличные от всего привычного, и про то, как они формируют мышление; программисты покажут, как автоматизировать расчёты в лабе и перепрошить старый принтер для печати миниатюрнейших шпор; юристы помогут выбить социальную стипендию, а о том, что творили химики с биологами, можно рассказывать часами.
Но чаще всего я засиживался у лазерщиков с радиотехниками. Возвращаясь с «птичьего рынка», они перебирали хлам, приобретённый у представителей древней могущественной цивилизации, а затем спаивали его в монструозную установку со стойким намерением получить возможность решетить лазером пивные банки. Там, играя с линзами, призмами и ртутными или натриевыми лампами, я впервые увидел атомные спектры.

Атомы — это всего лишь стабилизировавшиеся структуры из различных проявлений того, что когда-то должно быть описанным единой теорией поля. Пока мы будем воспринимать их как массивные ядра, удерживающие электроны на стационарных орбитах. Интереснее всего не сами дискретные стационарные состояния, а валюта этого квантового мира — разница между уровнями энергии. Происходит внешнее воздействие, и электронная плотность меняет конфигурацию. Затем она охотно возвращается в более энергетически выгодную форму, но каждое событие имеет цену, и электромагнитное поле получает пошлину ровно такую, сколько необходимо атому для возврата к оптимуму. И со скоростью света сведения о сделке вырисовывают гиперконус в пространстве и времени в поисках достойного наблюдателя.
Направляя луч фонарика на призму, я вижу проявление дисперсии света — пятно всех цветов радуги. Газовые лампы из коробки радиотехников не могут похвастаться таким обилием красок: видно лишь уединённые линии разных цветов — линейчатый спектр. Цвет отождествляется с частотой излучения и, следовательно, с разностью между уровнями энергии состояний, которые могут занимать электроны атомов возбуждённого газа.
Возможен и обратный процесс: белый свет (возбуждение электромагнитного поля множества различных частот), встретив на пути, скажем, облако газообразного натрия, теряет из своей братии фотоны определённых частот — тех, чьей энергии хватает ровнёхонько на конкретные электронные переходы. И тогда в радуге спектра появляются провалы, свидетельствующие о наличии на пути света некоторого вещества.
Собственно, так и были найдены натрий и другие элементы в атмосфере Солнца. Затем исследователи принялись наводить свои телескопы и спектроскопы на различные звёзды. Поначалу полученные спектры зарисовывали вручную. Позднее научились сохранять их на фотопластинах, что требовало огромную выдержку, так как снимки делались с огромной выдержкой (ха-ха) — по несколько часов нужно держать в окуляре уплывающий объект, регулируя всю эту громоздкую и чувствительную оптику.

Спектроскоп Хэггинса и фрагмент фотопластинки со спектрами абсорбции звёзд из созвездия Кормы
Полученные снимки классифицировались и каталогизировались кластером из органических компьютеров бесправной рабочей силой, а затем обобщались, анализировались и могучие умы наперебой публиковали свои объяснения содержания этих звёздных паспортов. В наше же время данные получаются и обрабатываются с помощью сложнейшего и точного оборудования.

Современные спектры звёзд с ярко выраженными линиями водорода или с обильным содержанием металлов. Источник
В статье «Почему электрон непременно должен упасть на ядро?» мы визуализировали решения уравнения Шрёдингера для атома водорода. Решение этого уравнения, помимо формы орбиталей, даёт нам собственные значения гамильтониана системы, уровни энергии, между которыми может переходить электрон. Разумеется, без учёта спина и релятивистских эффектов. Но этого достаточно, чтобы сравнить полученные линии переходов со спектрами поглощения звёздной атмосферы. Качаем данные предоставленные MUSE для какой-нибудь звёздочки, рисуем линии водорода и вуаля:

Вау. В этой звезде есть водород. А ещё спектр сдвинут в синюю область, значит звезда приближается к нам.
Более же точные измерения, скажем, линии Н-альфа помогают оценить доплеровский сдвиг, а значит скорость приближения/удаления звёзды или облака газа. А это очень важно для понимания динамики космических объектов.
Кривые вращения
You spin me right round, baby
Right round like a record, baby
Right round, round, round
Dead or Alive
Поначалу астрономия с астрофизикой нравились не особо — вычисления до неприличия приближенные, многие формулы феноменологические и изобилующие свободными параметрами, а все заключения строятся на интерпретациях шатких наблюдательных данных без перспектив на дальнейшее практическое использование. Но со временем прагматизм уступает осознанию ценностей фундаментальных наук, а скептицизм развеивается тщательным изучением различных моделей и пониманием границ их применимости.
Взять, к примеру, простейшую модель вращающегося диска, по радиусу которого равномерно нанесены точки. По мере увеличения расстояния от оси вращения скорости точек растут линейно.


Кривая вращения показывает, что скорость точек на диске прямо пропорциональна расстоянию от центра. К планетарным системам такая модель неприменима, так как группы тел, удерживаемые гравитацией, обладают большей гибкостью при вращении. Вместо этого у нас есть ньютоновская механика, а именно модель Кеплера. В этой модели большая часть массы сосредоточена в центре вращающегося объекта, а спутники свободно вращаются вокруг него. Приравняв силу тяжести к центростремительной, выясняем, что в планетарной системе скорость вращения обратно пропорциональна квадратному корню из радиуса:
Здесь полезно учитывать, что по мере перехода на всё большие орбиты увеличивается заключаемая в них масса. Построим кривую вращения для Солнечной системы:
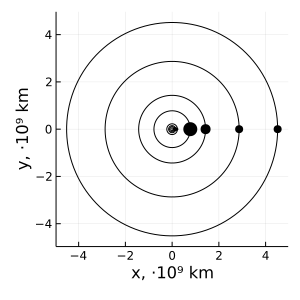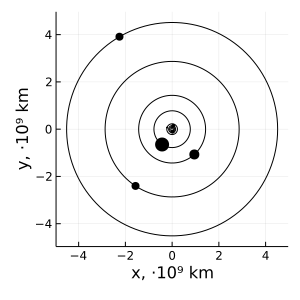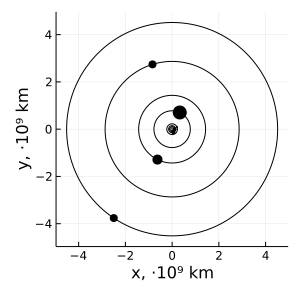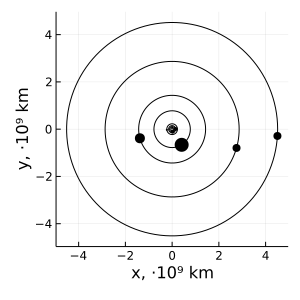
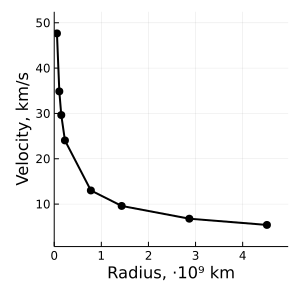
Попробуйте определить по графику орбитальную скорость нашей планеты. Она, как и остальные жильцы гравитационного колодца Солнца, чрезвычайно хорошо ложится на кеплеровскую кривую. И вроде ничто не должно мешать нам использовать нашу классическую модель на других космических системах и иных масштабах.
Например, можно было бы описать движение скоплений галактик, как это сделал Фриц Цвикки в 30-е годы прошлого века. Оценки давали слишком большие скорости, чтобы структуры оставались стабильными, поэтому возникло предположение, что существует большое количество пока не опознанной массы, удерживающей галактики вместе. Мысль не обрела особой популярности, и почти полстолетия она подтверждалась лишь редкими косвенными наблюдениями.
Переломный момент наступил после публикации Верой Рубин и соавторами ряда статей, где был выполнен анализ спектров светящегося вещества в галактиках. Галактика — это совокупность звёзд, пыли и газа. Большая часть этого газа находится в форме нейтрального водорода при низких температурах (< 300 К). Единственный электрон атома водорода находится в основном состоянии при этой температуре, и его спин сонаправлен со спином протона в ядре. Есть очень малая вероятность того, что электрон «перевернётся» в другую сторону — это происходит примерно раз в 11 миллионов лет. При этом переходе в более низкое энергетическое состояние высвобождается фотон радиоволнового диапазона (21 см). Радиоволны могут проникать сквозь пыль, поэтому регистрация такого излучения используется для изучения внутренних механизмов галактики. Крошечной вероятности испускания радиокванта противодействует огромное количество атомов водорода, присутствующих в галактике, так что мы постоянно наблюдаем это излучение.
Используя спектроскопию линии нейтрального водорода, Вера Рубин проанализировала доплеровский сдвиг различных участков в галактике M31 (Туманность Андромеды), а затем в ряде других галактик.

Спектрограмма галактики NGC 7541, сделанная Верой Рубин. Каждая из спектральных линий, излучаемых галактикой, представляет собой изображение галактики, растянутое слева направо в зависимости от длины волны (чётко видны пять изображений). Линии смещены в красную сторону на величину, которая зависит от скорости источника относительно нас. Галактика удаляется от нас из-за расширения Вселенной, но также она вращается вокруг своего центра, поэтому одна сторона удаляется от нас, а другая движется к нам. Это означает, что две половины галактики имеют немного разные красные смещения, как это видно по центральным линиям. Что примечательно, так это то, что красное смещение остаётся постоянным по мере удаления от центра. Если бы вся масса в галактике заключалась в звёздах и газе, то точки, расположенные дальше по обеим сторонам, имели бы больше похожих красных смещений, чем точки, расположенные ближе. А если построить кривые вращения, то они никак не хотят быть похожими на кеплеровские.
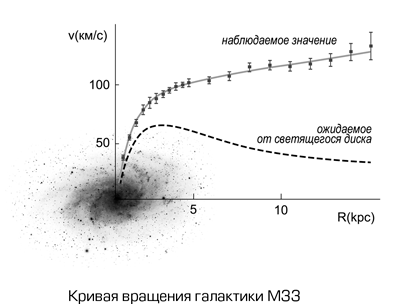
Со временем человечеству становилось доступно всё более точное оборудование для определения масс, расстояний и скоростей. Приспособьте копну оптических волокон к группе современнейших оптических телескопов, доведите их к прецизионным спектрографам и получите возможность определять скорость звёзд и газовых облаков с точностью до километров в секунду. Обильные данные выкладываются в открытый доступ и любой научный сотрудник (из незабаненной страны) получает возможность обработать их и проверить на них свою модель.

MaNGA (Mapping Nearby Galaxies at APO) получает спектры по всему профилю целевой галактики. Массив волокон пространственно сэмплирует конкретную галактику, затем сравниваются спектры, наблюдаемые двумя волокнами в разных местах галактики, и вычисляется, насколько сильно спектр центральных областей отличается от внешних областей, что позволяет строить карту скоростей
Давайте попробуем сами нарисовать галактическую кривую вращения. Воспользуемся базой данных Spitzer Photometry and Accurate Rotation Curves (SPARC), где имеются результаты измерений скоростей движения светящегося вещества в 175 галактиках. Вот пример кривых вращения по тамошним данным:
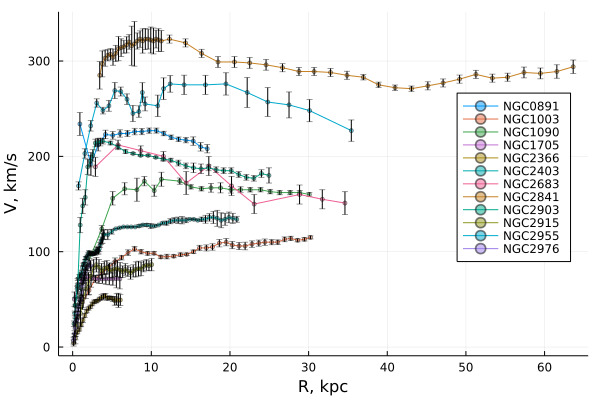
Я выбрал UGC03205, расположенную от нас в пятидесяти мегапарсеках (50 Мпк = 1.63e8 св.г. = 1.44e21 вёрст = 1.54e24 м).

Если до 10 кпк ещё есть спуск, то уже дальше по скоростям выходит полочка. График чертовски не похож на кеплеровскую кривую. К слову, в файликах есть скорости отдельных галактических компонентов: балджа, газа и диска, полученные из профилей светимости и наблюдаемой поверхностной яркости. При суммировании они должны были бы воспроизводить наблюдаемую галактическую кривую вращения.
Можно заметить, что у второго и третьего слагаемых есть множители, имеющие смысл отношения массы к светимости. Они являются варьируемыми параметрами, которые нужно подобрать так, чтобы суммарная скорость (красная линия) наложилась на наблюдаемую. Простая задача оптимизации на две переменные:
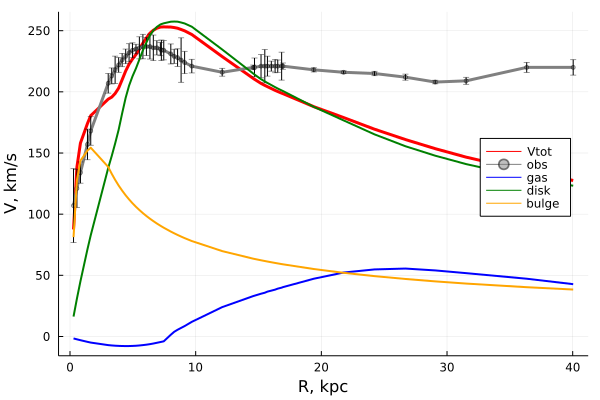
Вот только как ни старайся, но видимого вещества недостаточно — нужна ещё масса, которая будет позволять галактическим составляющим, находящимся дальше 15 кпк от центра UGC03205, иметь такую высокую скорость и не разлетаться во все стороны. Из ряда физических соображений можно получить распределение этой массы по галактике и добавить её вклад в общее распределение скоростей:
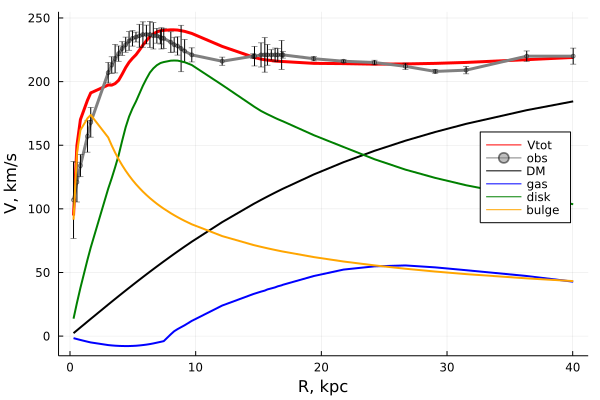
Какая бы ни была природа этой невидимой массы, пока она справляется с ролью костыля. А как обстоят дела в нашей родной Галактике? Взглянем на неё в миллиметровом диапазоне:

Источник изображения
Атомы могут образовывать молекулы, а наиболее распространёнными атомами во Вселенной являются H, He, С и О, поэтому логично предположить, что наиболее распространённые молекулы, которые могут быть сформированы, состоят из этих атомов. Для изучения Млечного Пути мы сосредоточимся на молекуле монооксида углерода (СО).
Молекулярные связи на самом деле не такие прочные, и излучение звёзд и раскалённых облаков может легко их разорвать, поэтому молекулы, подобные СО, можно найти только там, где они защищены от этого излучения, — в облаках газа и пыли. Ядра углерода и кислорода могут вращаться друг вокруг друга со скоростями, кратными определённым числам, точно так же, как электроны могут «вращаться» вокруг ядра атома в целочисленных энергетических состояниях, которые мы называем орбиталями. В микромире квантуется всё, даже вращение. Вспомните, как непринуждённо можно плавно увеличивать скорость кручения юлы, а затем представьте, что скорости можно переключать только рывками.
Целочисленное изменение вращения излучает конкретную единицу энергии. В данном случае свет, который мы называем фотоном миллиметрового диапазона. Этот фотон линий молекулярного вращения CO можно поймать радиотелескопом и использовать для определения физических свойств (таких как плотность и температура) межзвёздного газа. Построим кривую вращения Млечного Пути по данным СО-спектроскопии:

К сожалению, у нас нет распределений по скоростям отдельных компонент, но их можно получить с помощью мудрёных физических моделей, которые я здесь расписывать не буду. Если «с каждой формулой число читателей уменьшается в два раза», то из всего человечества останется около восьми смельчаков. На код и теорию ссылки будут приведены далее, но трижды подумайте, нужно ли вам портить сон и аппетит функциями Бесселя и квадратурами интегралов с бесконечными пределами.
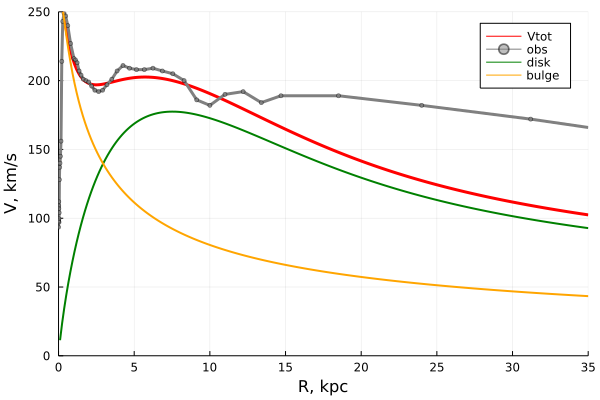

Та же картина — чтобы объяснить распределение скоростей, приходится добавить большое количество некой скрытой массы. Самое интересное, что со временем данные переполучаются со всё возрастающей точностью и различными способами. И прежде чем говорить словосочетание начинающееся на «тёмная…», взглянем на небо ещё раз, но в микроволновом диапазоне.
Космический микроволновый фон
Космологи часто ошибаются, но никогда не сомневаются.
Л.Д. Ландау
В начале шестидесятых NASA инициировало проект «Эхо» — первую программу по созданию спутниковой связи. На орбиту запустили пару пассивных рефлекторов. Устройства были крайне простые: сферы из плёнки с алюминиевым напылением, раздувающиеся за счёт газифицирующегося порошкообразного химического реагента. Эти спутники-баллоны должны были обеспечить ретрансляцию радиосигнала между станциями на Земле. Одной из таких станций была рупорно-параболическая антенна в Холмдейле.

15-метровый рефлектор со сверхмалым уровнем шума мог стать многообещающим инструментом для радиоастрономии. Задача по обновлению телескопа была поручена паре молодых, недавно получивших дипломы радиоастрономов Арно Пензиасу и Роберту Вильсону. Их первый проект предполагал использование рупорной антенны для измерения с точностью до двух процентов интенсивности излучения остатка сверхновой в созвездии Кассиопеи, который из-за своей яркости часто используется в качестве калибровочного источника.
Этот вид измерения очень сложен, так как микроволны из нашей собственной галактики образуют своего рода статические помехи, и, к сожалению, этот статический шум нелегко отличить от неизбежного электрического шума, вызванного случайным движением электронов внутри конструкции антенны или цепей внутри усилителя детектора. Кроме того, будет также небольшое количество помех, улавливаемых антенной из земной атмосферы, и всё это необходимо устранить.
Используя телескоп для изучения небольшого локализованного источника излучения, такого как звезда, можно направить антенну на звезду, собрать сигнал, а затем направить антенну в сторону, на пустую область пространства, и собрать сигнал фонового шума. Если затем сравнить два сигнала и посмотреть на разницу между ними, появится возможность нивелировать помехи и восстанавливать чистый сигнал от источника. Выглядит логично: любой шум, исходящий от цепей усилителя, антенной конструкции или от земной атмосферы, будет одинаковым независимо от того, направлена ли антенна на источник или на пустой участок неба.
Чтобы вычесть шум, Пензиас и Вильсон в 1964 году провели серию наблюдений на относительно короткой длине волны 7,35 см, где микроволновые сигналы от галактических источников считались незначительными. Они ожидали, что после вычитания известных источников фонового шума из измеренного выхода антенны, результат был бы равен нулю в пределах экспериментальной неопределённости. Однако, когда два исследователя начали проводить измерения, они были удивлены, обнаружив очень сильный сигнал микроволнового шума. Ещё более озадачивало то, что сила сигнала оказалась независимой от направления антенны, времени суток или времени года.
Источник не мог находиться в нашей Галактике, потому что, если бы это было так, то было бы ожидаемо увидеть такой же сильный сигнал, исходящий от других галактик, таких как наша ближайшая соседка Андромеда. Отсутствие зависимости от направления заставляло предположить, что микроволновые помехи исходили из Вселенной гораздо большего объёма, чем просто наша собственная галактика, однако Пензиас и Вильсон не могли избавиться от идеи, что, возможно, это излучение было просто шумом антенны, и они каким-то образом пропустили или не смогли идентифицировать его источник. Аппарат разобрали и тщательно очистили, не в последнюю очередь потому, что обнаружили пару голубей, устроившихся в горловине антенны и покрывших её «белым диэлектрическим материалом, который при комнатной температуре может быть источником электрического шума». Однако после демонтажа, очистки и восстановления антенны таинственный шум никуда не исчез.
В дальнейшем этот шум нарекли космическим сверхвысокочастотным (или микроволновым) фоновым излучением, или просто реликтовым излучением. На протяжении полувека его исследовали все детальней, запуская оборудование на аэростатах или посылая обсерватории на орбиту.
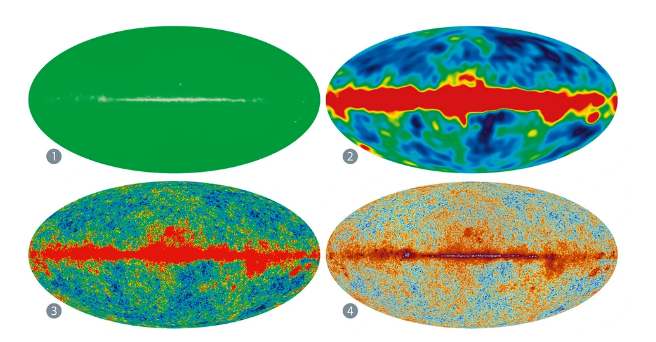
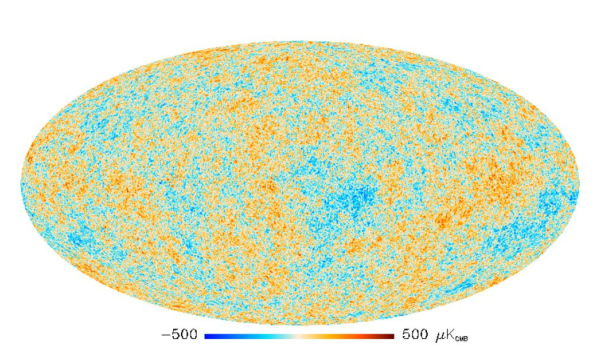
Панорамная карта анизотропии микроволнового фона. Источник изображения
1 — Так выглядело бы первое обнаружение реликтового излучения в 1964 году.
2 — На снимке COBE в начале 1990-х годов видно большую красную полосу с микроволновым излучением нашей Галактики.
3 — В 2001 году программа WMAP смогла проанализировать мельчайшие изменения температуры, улучшив детализацию в 70 000 раз.
4 — Миссия Planck использовала ещё более чувствительные инструменты для уточнения результатов, как показано на карте реликтового излучения 2015 года.
Перво-наперво, эта карта — проекция Моллвейде всего неба. Просто изображение глобуса на плоскости с сохранением площадей пятен, хотя в нашем случае мы смотрим на глобус изнутри. Во-вторых, на карте показана неоднородность температуры. Следует помнить, что в некоторых разделах физики температура может иметь различные определения, и конкретно в этом случае имеется в виду температура, связанная со спектральной плотностью излучения. Эта связь характеризуется формулой Планка, описывающей излучение, которое находится в тепловом равновесии с веществом при определённой температуре. Она применима для абсолютно чёрных тел любой формы вне зависимости от состава и структуры при условии, что размеры излучающего тела и деталей его поверхности гораздо больше длин волн, на которых тело излучает.
Так вот, космические обсерватории и наземные телескопы, расположенные где-нибудь в пустынях, сканируют небо с высоким разрешением. Данные с каждого детектора считываются с высокой скоростью (обычно > 50 Гц) и записываются вместе с информацией о наведении и другими вспомогательными параметрами. Алгоритмы построения карт представляют собой очень интересный пример работы с большими данными, поскольку они требуют очистки временных потоков путём фильтрации, выявления переходных событий и коррелированных шумов и в конечном счёте сжатия ~Тб данных до карт, которые обычно имеют размер 100 Мб или меньше.
Присмотримся к карте анизотропии реликтового излучения, составленной обсерваторией Planck и почищенной от засветки Млечного Пути. Эффективная температура микроволнового фона равна 2,725 К, а карта показывает перепады до половины милликельвина от этого числа. Шум как шум, ну и местами кучкования. И вот как раз анализ соотношений характеристик этих пятнышек несёт огромное количество информации.
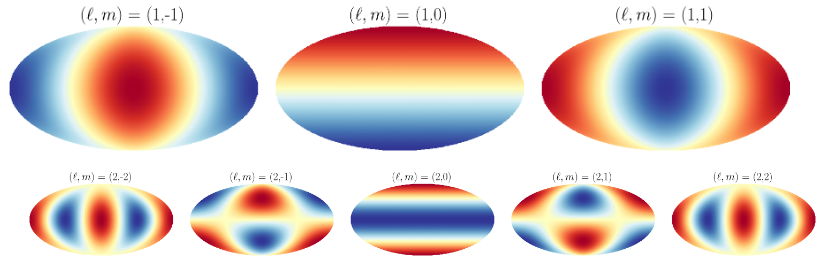
Чтоб было удобней изучать карту, получим спектр мощности. Анализируя какой-либо сигнал, любой образованный гражданин уверенно строит спектр, выполнив преобразование Фурье. В данной же ситуации нужно преобразовывать поверхность сферы, что эффективно реализуется с помощью разложения по сферическим гармоникам. Они образуют ортогональный базис на поверхности сферы, что делает их идеальным выбором для разложения температуры реликтового излучения на независимые моды:
Каждое слагаемое это моно-, ди-, квадру- и прочие -поли с разными весами.
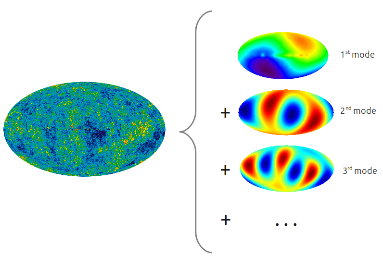
И так вся карта представляется взвешенной суммой наших пятнышек:
А если теперь отложить на графике вклад каждой моды в изменение температуры реликтового излучения, получатся спектры мощности, где каждый пик несёт в себе важную космологическую информацию:

Воспринимаем график как гистограмму, где по оси абсцисс перечисляются номера мод или угловая частота, а по оси ординат — вес каждой моды на карте анизотропии. Чтобы научиться понимать эти графики, пробежимся по физике процессов в молодой Вселенной.
▍ Истоки реликтового излучения
Наше понимание физики, лежащей в основе описанных выше наблюдений, восходит к концу 1960-х годов, когда Джим Пиблз из Принстонского университета и аспирант Джер Ю поняли, что ранняя Вселенная должна была содержать звуковые волны (почти в то же время Яков Зельдович и Рашид Сюняев из Московского института прикладной математики пришли к очень похожим выводам).
Было время, когда содержимое Вселенной было настолько горячим, что электроны и протоны не могли объединиться в стабильные атомы, поскольку средняя энергия электронов превышала энергию ионизации водорода. В этих экстремальных условиях отдельный фотон не смог бы пройти далеко, не будучи рассеянным или поглощённым электроном. Среднее время между взаимодействиями фотона с газом из ядер и электронов было чрезвычайно коротким, и хотя Вселенная сначала очень быстро расширялась, с точки зрения отдельного фотона, электрона или ядра расширение было достаточно медленным, так что каждый фотон рассеивался, поглощался и переизлучался много раз по мере того, как растягивалось пространство. Любая система, в которой отдельные составляющие успевают многократно взаимодействовать, обычно достигает состояния равновесия. Хотя отдельные скорости и энергии составляющих частиц могут изменяться, общие статистические распределения этих скоростей и энергий остаются постоянными. Такое равновесие часто называют тепловым равновесием, потому что оно характеризуется определённой температурой, которая по сути одинакова во всей системе.
Когда масштабы наблюдаемой Вселенной увеличились до одной тысячной от их нынешнего размера — примерно через 380 000 лет после Большого взрыва — температура газа уменьшилась настолько, что протоны смогли захватить электроны и стать атомами. Этот переход, названный рекомбинацией, резко изменил ситуацию. Фотоны больше не рассеивались при столкновениях с заряженными частицами, поэтому впервые они начали путешествовать в пространстве практически беспрепятственно. Фотоны, испускаемые из более горячих и плотных областей, были более энергичными, чем фотоны, испускаемые из разрежённых областей, поэтому картина горячих и холодных пятен, вызванных звуковыми волнами, была заморожена в реликтовом излучении.
Представим, что мы находимся в центре простейшей двумерной вселенной со стоячими волнами, где сразу после рекомбинации фотоны получают возможность достигнуть удалённого наблюдателя. Здесь растущая окружность показывает радиус обзора.

Сразу после рекомбинации вы видите изотропное реликтовое излучение (первые несколько кадров синий кружок в центре, одинаковый во всех направлениях), так как только фотоны из области вокруг центра успели достичь вас.
С течением времени вы видите фотоны из более отдалённых областей (жёлтые траектории). Сначала вы видите квадрупольную вариацию вокруг себя (красный и синий под углами 90 градусов), затем октуполь и т. д. К текущей эпохе примерно через 10 миллиардов лет вы видите очень тонкую структуру углового масштаба температуры реликтового излучения. Кольцо, которое вы видите в конце анимации выше, содержит много красных и синих полос — с течением времени вас достигают фотоны со всё более дальних областей и количество пятен на вашем небе увеличивается. Пространственная неоднородность при рекомбинации превратилась в угловую анизотропию.
Обратите внимание, что в центре приведённой выше диаграммы нет ничего особенного. Выберите другую точку в пространстве, и вы увидите, что происходит тот же процесс. Фотоны реликтового излучения распространяются во всех направлениях при рекомбинации. Мы показали только те, которые увидел наблюдатель в центральной точке.
Итак, с самого начала космос был неоднороден. Одной из возможных причин считается космологическая инфляция, взрастившая квантовые флуктуации до огромных масштабов. Об этой стадии жизни Вселенной поговорим как-нибудь в следующий раз, а пока нам важно, что в нашем фотонно-барионном газе были температурные неоднородности. Эти возмущения становятся причиной колебаний плотности энергии в первичной плазме.
Доказательства, подтверждающие теорию инфляции, были обнаружены в подробном образце звуковых волн в реликтовом излучении. Поскольку инфляция произвела все возмущения плотности сразу, по существу, в первый момент создания фазы всех звуковых волн были синхронизированы. В результате получился звуковой спектр с обертонами, как у музыкального инструмента. Представьте, что вы дуете во флейту. Основная частота звука соответствует волне с максимальным смещением воздуха на концах трубки и минимальным смещением в центре. Длина волны основной моды в два раза больше длины флейты. Но звук также имеет ряд обертонов, соответствующих длинам волн, которые составляют целые доли основной длины волны: половина, треть, одна четвёртая и так далее. Иными словами, частоты обертонов в два, три, четыре и более раз превышают основную частоту. Обертоны — вот что отличает скрипку Страдивари от обычной скрипки — они добавляют насыщенность звуку.

Звуковые волны в ранней Вселенной похожи, за исключением того, что теперь мы должны представить волны, колеблющиеся во времени, а не в пространстве (стоячие волны). Волны основной частоты берут начало при инфляции и заканчиваются при рекомбинации примерно через 380 000 лет. Предположим, что некоторая область пространства имеет максимальное положительное смещение, т. е. максимальную температуру при инфляции. По мере распространения звуковых волн плотность области начнёт колебаться, сначала направляясь к средней температуре (минимальное смещение), а затем к минимальной температуре (максимальное отрицательное смещение). Волна, из-за которой область достигает максимального отрицательного смещения именно при рекомбинации, является фундаментальной волной ранней Вселенной.
Обертоны имеют длину волны, которая составляет целые доли основной длины волны. Колеблясь в два, три и более раза быстрее основной волны, эти обертоны заставляют меньшие области пространства достигать максимального смещения, положительного или отрицательного, при рекомбинации. Как космологи выводят эту закономерность из реликтового излучения? Они отображают величину колебаний температуры в зависимости от размеров горячих и холодных точек на графике — спектре мощности.
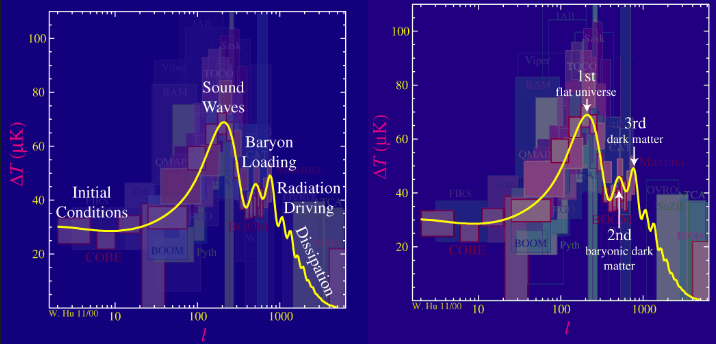
Результаты показывают, что области с наибольшими вариациями простираются примерно на один градус по небу, что почти вдвое превышает размер полной Луны (во время рекомбинации эти области имели диаметр около одного миллиона световых лет, но из-за 1000-кратного расширения Вселенной с тех пор каждая область простирается почти на один миллиард световых лет в поперечнике). Первый и самый высокий пик в спектре мощности свидетельствует о фундаментальной волне, максимально сжимавшей и разрежавшей области плазмы в момент рекомбинации. Последующие пики в
