Суперэллипс — фигура, которую многие видят каждый день, но не догадываются об этом
Приветствую Вас! Сегодня мы поговорим об интересной кривой, у которой есть своё название — суперэллипс.
Оглянитесь вокруг. Какие фигуры вы видите? Скорее всего, большинство фигур имеет либо прямые (острые, тупые) углы либо эллипсоидные (не всегда идеально круглые) границы. Однако, существуют и гибриды. Суперэллипсы — это семейство кривых, которые лежат где-то между эллипсами и прямоугольниками.
Для начала вспомним, что из себя представляет обычный эллипс — кривую второго порядка:

Коэффициенты a и b определяют «приплюснутость» эллипса по горизонтали и вертикали соответственно:

Но что, если вторые степени заменить чем-то другим? Если возвести в куб, в четвертую степень и т.д?
В 1959 году в шведском Стокгольме был объявлен конкурс на проектирование кольцевой развязки одной из городских площадей. Этот район находился там, где две широкие магистрали пересекались в центре города, поэтому требовалось не перекрыть транспортные потоки, да еще и обеспечить пешеходную зону уровнем ниже:

Площадь Сергеля
Архитектор Пит Хейн искал наиболее эстетичную, но и эффективную форму, о чем писал:
Человек — это животное, которое рисует линии, о которые он сам потом спотыкается. Всегда цивилизации наблюдались две тенденции: одна — к прямым линиям и прямоугольным узорам, а другая — к круговым линиям. Для обеих тенденций есть причины, механические и психологические. Вещи, сделанные с помощью прямых линий, хорошо сочетаются друг с другом и экономят место. И мы можем легко перемещаться — физически или мысленно — по предметам, сделанным с круглыми линиями.
Но мы в смирительной рубашке, вынуждены принимать то одно, то другое, когда часто какая-то промежуточная форма была бы лучше. Рисовать что-то от руки — например, многоуровневое дорожное кольцо, которое они пробовали в Стокгольме, — не годится. Суперэллипс решил проблему. Он не круглый и не прямоугольный, а что-то среднее. Тем не менее, она фиксирована, она определенна — в ней есть единство.
Уравнение суперэллипса в общем виде записывается следующим образом:

В зависимости от соотношения параметра n можно получить целую россыпь фигур.
Когда n приближается к нулю, кривая вырождается в две прямые пересекающиеся линии вдоль осей.
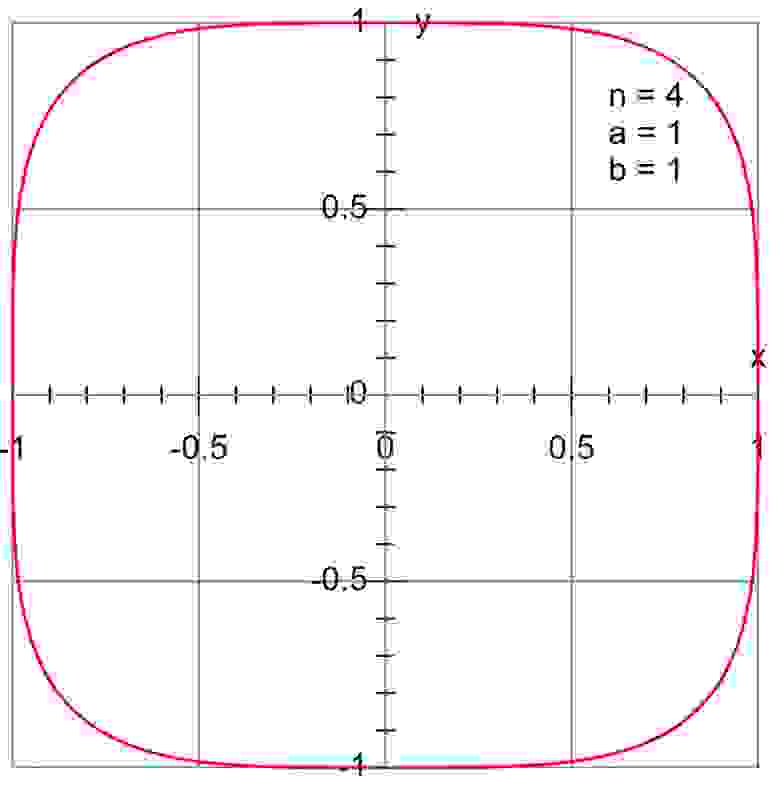
При 0 Когда n = 1, вы получаете ромб с вершинами на осях координат. При 1 Когда n = 2, вы получаете эллипс (или, если a и b равны — окружности). Если значение n > 2, у вас получается суперэллипс. (при проектировании площади, о которой я говорил выше, использовался параметр 2,5). По мере приближения n к бесконечности получаем прямоугольник. Сквиркл — особый суперэллипс с n=4 Стоит отметить, что, хотя суперэллипсы могут выглядеть так, как будто у них прямые стороны, соединенные кривыми, на самом деле они изогнуты по всему периметру. Даже там, где сегмент выглядит прямым, он на самом деле слегка изогнут, а кривизна изменяется повсюду непрерывно. Если вы повернете суперэллипс вокруг главной оси, получится суперяйцо, которое устойчиво относительно своих биологических аналогов: Форму суперэллипса имеют архитектурные объекты, предметы интерьера, логотипы брендов и команд: Однако подавляющее число людей впервые увидело суперэллипс…когда взяли в руки Iphone! Дело в том, что начиная c шестой версии iOs, дизайнеры перестали использовать прямоугольники с закруглением, а перешли к суперэллипсам: По ощущениям здесь используется суперэллипс с коэффициентом n = 5…7. Если и этого недостаточно, то знайте, что супСуперэллипс — фигура, которую многие видят каждый день, но не догадываются об этомерэллипс фигурировал в статье «Геометрическое моделирование и гидродинамический анализ плавающих сперматозоидов», жаль только, что этой публикации нет в открытом доступе. Больше математики в Telegram — «Математика не для всех»