Суп с котом: забавная задачка с LeetCode14.08.2023 20:31

Есть на LeetCode задачка. Medium уровня, на динамическое программирование, ничего особенного. Однако, если присмотреться внимательнее, она окажется интереснее, чем на первый взгляд. Кроме того, можно получить более быстрое решение, чем «официальное».

Условие (в адаптации для постсоветского читателя)

Недалеко от вокзала, есть маленькая столовая. Каждое утро в ней варят две одинаковых кастрюли супа: один с говядиной , другой, собственно, с котом . Порция супа составляет 100 миллилитров.

Клиенты каждой категории приходят в случайном порядке, каждая категория с вероятностью %.

Если какого-то вида супа для текущего клиента не хватило — ему подают сколько есть, не доливая ни того, ни другого. При этом заказ считается исполненным.

При заданном объёме кастрюли мл требуется определить, какова вероятность того, что говядина закончится раньше, и припозднившиеся гости будут жрать кушать только и исключительно несчастного кота. Кроме того, к ответу надо добавить 1/2 вероятности того, что оба супа закончатся одновременно. Результат требуется получить с погрешностью не более $10^{-5}$ .

Объем кастрюли может принимать значения от до 10^9 .

Наблюдения и размышления

Прежде всего, заметим, что объем половника у них мл, поэтому, вместо того, чтобы считать в миллилитрах, будем считать в половниках. Тогда объём кастрюли будет n/25 половников. Если не кратно , то округляем в большую сторону — как указано в условии, остатки считаются за полную порцию.

В начальный момент у нас имеется $m_A[0]= \lceil n/25 \rceil$ половников говядины и $m_B[0]= \lceil n/25 \rceil$ половников кота.
После первого заказа может остаться:

$m_A[1]=m_A[0]-100/25; \space m_B[1]=m_B[0]$ , если гость особо уважаемый;
$m_A[1]=m_A[0]-75/25; \space m_B[1]=m_B[0]-25/25$ , если гость просто уважаемый;
$m_A[1]=m_A[0]-50/25; \space m_B[1]=m_B[0]-50/25$ , если гость обычный;
$m_A[1]=m_A[0]-25/25; \space m_B[1]=m_B[0]-75/25$ , если гость алкаш.

Или, после -го заказа:

$m_A[i]=m_A[i-1]-4; \space m_B[i]=m_B[i-1]$ , если гость особо уважаемый;
$m_A[i]=m_A[i-1]-3; \space m_B[i]=m_B[i-1]-1$ , если гость просто уважаемый;
$m_A[i]=m_A[i-1]-2; \space m_B[i]=m_B[i-1]-2$ , если гость обычный;
$m_A[i]=m_A[i-1]-1; \space m_B[i]=m_B[i-1]-3$ , если гость алкаш.

Тут мы, внезапно, замечаем, что общее количество супа с каждой порцией уменьшается ровно на половника, а разность m_B-m_A увеличивается либо на 4, либо на 2, либо не меняется, либо уменьшается на 2. Учитывая, что с утра m_B-m_A = 0 , она всегда чётная, как и сумма, которая в начальный момент m_B+m_A = 2m_B .

Введём новые переменные: $s = \frac{m_B+m_A}{2}$ и $d = \frac{m_B-m_A}{2}$ .

В начальный момент $s[0] = \lceil n/25 \rceil ; \space d[0] = 0$ .

После -го заказа эти величины меняются следующим образом:

s[i] = s[i-1]-2 $d[i] = d[i-1]+[-1;0;1;2]|_{p=0.25}$

Рассмотрим вероятность P[i,D] того, что после заказа разность равна . Если в этот момент d[i]=D , значит:

либо перед этим было , но пришёл особо уважаемый гость и разность изменилась на ;
либо было , но пришёл просто уважаемый гость и разность изменилась на ;
либо было , пришёл обычный гость и разность не изменилась;
либо было , но пришёл алкаш и разность изменилась на .

Все эти события имеют место с вероятностью 0.25 . Тогда:

$\begin{split} P[i,D] &= P[i-1,D-2] \cdot 0.25 + P[i-1,D-1] \cdot 0.25 +\\ &+P[i-1,D] \cdot 0.25 + P[i-1,D+1] \cdot 0.25 \end{split}$

Таким образом, если мы создадим массив P[i,D] , зададим $P[0,:]=0; \space P[0,0]=1$ , то сможем последовательно посчитать вероятности после каждого заказа.

Но в какой-то момент один (или оба) супа закончатся. Когда это произойдёт?

Возвращаясь от наших переменных $s,\space d$ обратно к количествам супов, получим:

$m_А=s-d; \space m_B=s+d$

Количество супа с говядиной становится равным при d[i]=s , а супа с котом при d[i]=-s . То есть, как только будет достигнуто состояние, в котором $|d[i]| \ge s$ , мы должны прекратить сервировку. Это значит, что соответствующие им вероятности P[i,D] , где $|D| \ge s$ , не внесут вклада в вероятности последующих событий и их надо обнулить. Если при этом первым закончился суп с говядиной, то есть d[i]>0» src=«https://habrastorage.org/getpro/habr/upload_files/449/fa8/435/449fa8435047f8a63ef7f2b6f4d3bcd4.svg» />, то мы должны сначала добавить эту вероятность к окончательному ответу.</p>

<p>А когда закончатся оба супа, тогда их полусумма <img alt= станет равна . Таким образом, максимальное количество порций равно $\lceil s/2 \rceil$ , при чем последняя может быть неполной.

Рассмотрим, например, s[0]=7 .

Рисунок 1

Возможные состояния супов на каждом шаге отмечены кружочечком.

Границы серой области показывают уменьшение на каждом шаге. Если d[i] попало в серую область, значит после данного заказа какой-то из супов закончился. Если закончился суп с говядиной — кружок зелёный, если закончился суп с котом — красный, если оба — двухцветный.

В голубых кружочках указана искомая вероятность того, что суп с говядиной закончится раньше. Для каждого шага она равна сумме всех зелёных значений, лежащих ниже или на том же уровне (двухцветный входит с коэффициентом 0.5 ).

Стрелками показано, какое состояние может получиться на следующем шаге (чтобы не загромождать, показаны только крайние случаи).

Отметим, что состояния, где один из супов закончился, на последующие не влияют, но если бы мы продолжали их строить, то они давали бы вклад только в серой области (отмечено прозрачной зеленой и красной заливкой) — если суп закончился, то обратно он не появится. Запомним этот факт, он нам понадобится позже.

Рассмотрим также случай для чётного s[0] .

Рисунок 2

Мы видим, что для нечетного s[0] и следующего за ним четного s[0] количество раздач не меняется.

Алгоритм №1. Динамическое программирование

Таким образом стандартное решение данной задачи в неоптимизированном случае выглядит следующим образом.

Находим начальное $s0= \lceil n/25 \rceil$
Создаем массив вероятностей , состоящий из $\lceil s0/2 \rceil + 1$ строк, $2 \cdot s0+1$ столбцов. Обозначим индекс элемента соответствующего . Пусть индексация начинается с 0, тогда . Строка соответствует началу дня, когда порций съедено, строка $\lceil s0/2 \rceil$ — когда оба супа кончились;
Задаём , все остальные элементы в этой строке равны ;
Инициализируем переменную, в которой будем хранить результат ;
Инициализируем переменную, в которой будем хранить текущее значение полусуммы ;
Запускаем цикл по строкам от до $\lceil s0/2 \rceil$ включительно;
Вычисляем на текущем шаге: . Если получилась меньше , то присваиваем (любой остаток считается полноценной порцией);
Запускаем цикл по всем столбцам от до $2 \cdot s0$ ;
Для каждого элемента строки считаем вероятность:
$\begin{split} P[i,j] &= P[i-1,j-2] \cdot 0.25 + P[i-1,j-1] \cdot 0.25 \\ &+ P[i-1,j] \cdot 0.25 + P[i-1,j+1] \cdot 0.25 \end{split}$
Если индекс переполняется, соответствующее слагаемое не учитываем;
Если оба супа закончились одновременно $j=d0 \space and \space s=0$ , прибавляем половину к ;
Иначе если только суп с котом закончился $j-d0 \le -s$ , зануляем его ;
Иначе если закончился суп с говядиной $j-d0 \ge s$ , прибавляем полученную вероятность к ответу и зануляем ;
Переходим к следующему элементу и повторяем 9–13;
Переходим к следующей строке и повторяем 9–13;
Ответ находится в .

Вот программка на C++. Разумеется, можно сделать красиво, можно заметить, что массив избыточен, что нам надо хранить только предыдущую и следующую строчки и т.п.

double soupServings(int n) {
        int s0 = (n-1)/25+1;
        
        vector> P((s0+1)/2+1, vector(2*s0+1,0.));

        int d0 =s0;
        P[0][d0] = 1.;

        double ans = 0.;
        int s = s0;

        for (int i = 1; i< P.size(); ++i) {
            s -= 2;
            if (s<0) s = 0;
            for (int j = 0; j< P.front().size(); ++j) {
                
                if (j-2 >= 0) P[i][j] += P[i-1][j-2]*0.25;
                if (j-1 >= 0) P[i][j] += P[i-1][j-1]*0.25;
                P[i][j] += P[i-1][j]*0.25;
                if (j+1 < P.front().size()) P[i][j] += P[i-1][j+1]*0.25;

                if (j==d0 && s <= 0) {
                    ans += P[i][j]*0.5;
                    P[i][j] = 0;
                }
                else if (j-d0 >= s) {
                    ans += P[i][j];
                    P[i][j] = 0;
                }
                else if (j-d0 <= -s) P[i][j] = 0;
            }
        }

        return ans;

И все бы хорошо, но временная сложность получается O(n^2) , также как и затраты памяти. А допустимое значение может быть аж 10^9 . То есть нам надо будет несколько эксабайт памяти и очень много времени.

Однако, мы можем заметить, что с ростом ответ приближается к 1.0 , и при n>5000» src=«https://habrastorage.org/getpro/habr/upload_files/d68/fbf/b90/d68fbfb90a26293ccfea07aac914f886.svg» /> отличается от <img alt= менее, чем на $10^{-5}$ . А требуемая точность и есть $10^{-5}$ . То есть мы можем просто добавить в начале строчку if (n>5000) return 1.;. При n=5000 мы имеем s[0]=200 , то есть получается массив $101 \times 401$ , а если оптимизировать и того меньше. Именно такой тип решения и предлагается в качестве «официального» на LeetCode.

Наблюдения и размышления (продолжение)

Вышеизложенное всем известно и никому не интересно. А что, если придумать решение O(n) по времени и O(1) по затратам памяти? Давайте придумаем.

Прежде всего вспомним, что область влияния состояний, которые соответствуют закончившемуся супу, ограничена серыми областями на рисунке. Что будет, если мы не будем обнулять эти вероятности? Раз они остаются в серой зоне, мы можем их оставить «на потом», и сложить уже только на последнем шаге.

Рисунок 3.

Мы получили весьма интригующую картину. Вероятности оказались симметричны, более того, получившееся дерево одинаково для всех , разница только в том, где его обрубать.

К сожалению, ответ не совпадает. И мы видим, почему. Состояние с d[i]=-1 на предпоследнем шаге влияет на правую серую область и на центральное значение, а также состояние с d[i]=+1 на предпоследнем шаге влияет на центральное.

Тогда давайте уменьшим число шагов на 1, а последний сделаем «ручками». Для нечетных надо дополнительно обработать только один белый кружок d[i]=0 .

Рисунок 4.

Для четных ручками будем обрабатывать аж 3 кружка: d[i] = -1, 0, 1

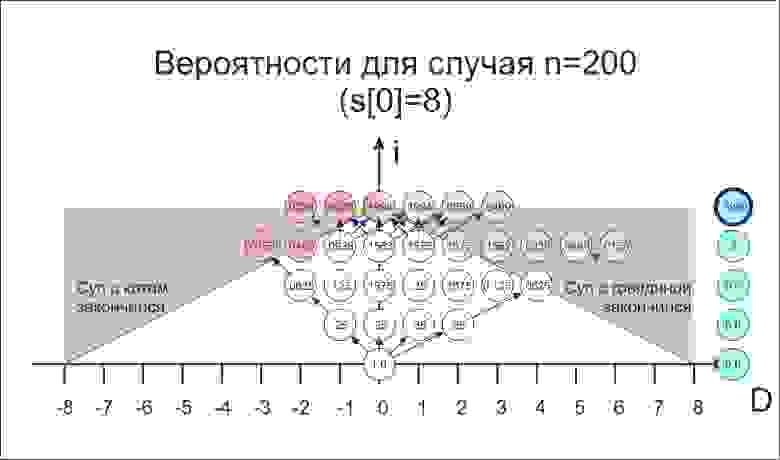
Рисунок 5.

Ура! Получилось.

Но что дальше? Нам все равно придется строить пирамиду. Или нет?

Избавившись от граничный условий, мы получили следующую задачу. Есть целое число , в начальный момент d[0]=0 . На каждом шаге к нему добавляется , , , с одинаковой вероятностью, обозначим это событие как $[-1,0,1,2]|_{p=0.25}$ . Найти вероятность того, что на шаге получится d[i]=D .

Если бы у нас было, к примеру, только два возможных исхода, мы получили бы биномиальное распределение https://ru.wikipedia.org/wiki/Биномиальное_распределение.

О биномиальном распределении

Пусть мы бросаем монетку раз. Какова вероятность, что выпадет ровно орлов, считая, что вероятность выпадения орла и решки одинакова? Посчитаем количество таких исходов. Выпишем подряд индексы бросков 0, 1, 2, 3, 4, 5... . Переставим их так, чтобы все броски, при которых выпал орёл, были в начале списка. То есть для бросков, соответствующих первым индексам выпал орел, для остальных решка.

$i_{орелЪ}[0], i_{орелЪ}[1], ..., i_{орелЪ}[x], \space \space i_{решка}[0], i_{решка}[1], ... , i_{решка}[i-x]$

Каждый индекс в списке встречается ровно раз. Всего имеем вариантов расположения индексов. Однако, если мы перетасуем индексы, которые соответствуют выпадению орла, только среди «своих», мы получим тот же самый случай. Аналогично для решки.

Таким образом, надо разделить общее число перестановок на число перестановок отдельно орлов и число перестановок отдельно решек. Получаем биномиальный коэффициент https://ru.wikipedia.org/wiki/Биномиальный_коэффициент:

$\binom{i}{x} = \frac{i!}{x!(i-x)!}$

Это число возможных исходов серии бросков, когда выпадает ровно орлов. Чтобы найти вероятность, надо разделить его на общее число возможных исходов, которое равно 2^i — для каждого из бросков возможны два варианта, а всего бросков .

Но у нас не два, а четыре варианта для каждого шага. И тут мы вспоминаем, что четыре — это дважды два. Что если вместо каждого броска с четырьмя исходами, делать два броска с двумя исходами? Вместо того, чтобы выбирать одно из четырех возможных слагаемых $[-1, 0, 1, 2]|_{p=0.25}$ , выберем сначала одно из двух $[0, 2]|_{p=0.5}$ , а потом еще одно из другой пары $[0, -1]|_{p=0.5}$ .

Выпишем все возможные исходы:

выбрали и : $d \rightarrow d+0-1=d-1$ , вероятность ;
выбрали и : $d \rightarrow d+0+0=d+0$ , вероятность ;
выбрали и : $d \rightarrow d+2-1=d+1$ , вероятность ;
выбрали и : $d \rightarrow d+2+0=d+2$ , вероятность .

Получается, два бинарных события в сумме дают нам искомое событие с четырьмя исходами. Такой трюк можно провернуть далеко не в каждом случае, но здесь можно.

Какова вероятность, что после пар бросков d[i]=D ?

Пусть в паре $[0, 2]|_{p=0.5}$ раз выпала двойка, вероятность этого равна $2^{-i}\binom{i}{q}$ .

В свою очередь, в паре $[0, -1]|_{p=0.5}$ раз выпала , вероятность $2^{-i}\binom{i}{k}$ .

Чтобы получить необходимо, чтобы $q \cdot 2 + k \cdot (-1)=D$ . Просуммируем вероятности:

$P[i,D]=\sum_{2q-k=D} \left[ 2^{-i}\binom{i}{q} \cdot 2^{-i}\binom{i}{k} \right]$

Выразим через :

$P[i,D]=2^{-2i}\sum_{q} \left[ \binom{i}{q} \binom{i}{2q-D} \right]$

Видим, что не может быть меньше, чем $max(0,\lceil D/2 \rceil)$ , и больше, чем $min(i,\lfloor (i-D)/2 \rfloor)$ .

$P[i,D]=2^{-2i}\sum_{q=max(0,\lceil D/2 \rceil)}^{min(i, \lfloor (i+D)/2 \rfloor )} \left[ \binom{i}{q} \binom{i}{2q-D} \right]$

Формулу получили, осталось применить её к нашей задаче.

Посчитаем вероятность того, что на шаге супа с котом больше или столько же, сколько супа с говядиной $d[i] \le 0$ . Почему не наоборот? Потому что это число меньше, а значит, при одинаковой относительной погрешности вычисления будем иметь меньшую абсолютную погрешность. Кстати отметим, что минимальное возможное значение d[i] на каждом шаге равно . Оно соответствует случаю, когда каждый раз выпадала .

Вернемся к исходной форме выражения:

$P[i,d[i] \le 0]=2^{-2i}\sum_{2q-k \le 0} \sum \left[ \binom{i}{q} \binom{i}{k} \right]$

не может быть больше, чем , и в то же время $0 \le 2q \le k \le i$ . Если внешнее суммирование делать по , то его пределы будут от до $\lfloor i/2 \rfloor$ . Тогда:

$P[i,d \le 0]=2^{-2i}\sum_{q=0}^{\lfloor i/2 \rfloor}\sum_{k = 2q}^{i} \left[ \binom{i}{q} \binom{i}{k} \right]$

Однако, если мы применим данную формулу на предпоследнем шаге, результат будет включать вероятности, которые мы хотели обрабатывать «ручками», для случая d[i]=0 , а для четных также и d[i]=-1 . К тому же, нам будут нужны сами эти вероятности отдельно, а также вероятность d[i]=1 для четных .

Выпишем формулы для них:

$P[i,0]=2^{-2i}\sum_{q=0}^{\lfloor i/2 \rfloor} \left[ \binom{i}{q} \binom{i}{2q} \right]$ $P[i,-1]=2^{-2i}\sum_{q=0}^{\lfloor (i-1)/2 \rfloor} \left[ \binom{i}{q} \binom{i}{2q+1} \right]$ $P[i,1]=2^{-2i}\sum_{q=1}^{\lfloor (i+1)/2 \rfloor} \left[ \binom{i}{q} \binom{i}{2q-1} \right]$

Посмотрев на рисунки 4 и 5 и подумав, получим окончательное выражение для искомой вероятности того, что суп с говядиной закончится раньше. Вспоминаем, что максимальное количество порций $\lceil s0/2 \rceil$ , значит на предпоследнем шаге $i = \lceil s0/2 \rceil -1$ :

для нечетных s:
$ans = 1 - P[i,d \le 0] + P[i,0] \cdot 0.25 \cdot 2.5 = 1 - P[i,d \le 0] + P[i,0] \cdot 0.625$
для четных s:
$\begin{split} ans &= 1 - P[i,d \le 0] - P[i,1] + P[i,-1] \cdot 0.25 \cdot 1.5 + \\&+ P[i,0] \cdot 0.25 \cdot 2.5 + P[i,1] \cdot 0.25 \cdot 3.5 = \\ &= 1 - P[i,d \le 0] + P[i,-1] \cdot 0.375 + P[i,0] \cdot 0.625 - P[i,1] \cdot 0.125 \end{split}$

Теперь бы все это посчитать.

Для начала, нам нужны биномиальные коэффициенты. Поскольку у нас фиксировано, можно рассчитать их заранее. Проницательно отметив, что

$\binom{i}{k}=\binom{i}{i-k},$

будем считать только половину из них. Но если велико, то и биномиальные коэффициенты большие, может случиться переполнение. К счастью, нам нужны не сами коэффициенты, а вероятности, то есть:

$2^{-i}\binom{i}{k}$

Тут возникает обратная проблема: $2^{-i}\binom{i}{0}=2^{-i}$ — очень маленькая величина.

А так как факториалы считаются последовательно, следующий выражается через предыдущий, то умножение на даст .Чтобы решить эту проблему, будем делить на степени двойки постепенно. Сначала на 1, потом на 4, потом на 16 и т.д. Почему именно так? Потому что мы считаем только половину из биномиальных коэффициентов, соответственно, к концу дойдет до нужной степени. А самое главное, наибольшее значение как раз в середине:

$\max_k{\binom{i}{k}}=\binom{i}{i/2}$

Параллельно будем считать сумму:

$2^{-i}\sum_{j=0}^{k}\binom{i}{k}$

Чуть раньше, вы наверное, удивлялись, как же так, ведь $P[i,d \le 0]$ содержит две суммы, почему же я заявляю время O(n) ? А потому, что суммы по считается здесь один раз и за линейное время. Очень удобно: посчитал коэффициент и сразу прибавил.

Кстати, вы помните, что $2^{-i}\sum_{j=0}^{i}\binom{i}{k}=1$ ?

Алгоритм №2.1. Расчет вероятностей биномиального распределения

Создаём массивы для хранения биномиальных коэффициентов и сумм размером $\lfloor i/2 \rfloor + 1$ каждый;
Инициализируем переменную , в которой будем хранить текущий биномиальный коэффициент деленный на какую-то (сами не знаем, какую, но можем сочинить) степень двойки;
Записываем первый коэффициент $binomials[0]=val \cdot 2^{-i}$ (помним, что целочисленные степени двойки считаются очень просто);
То же самое записываем в первую ячейку массива сумм ;
Запускаем цикл по от до $\lfloor i/2 \rfloor$ включительно;
Модифицируем значение:
$val = val*\frac{i+1-k}{i}$
Вы можете легко получить это выражение, если разделите $\binom{i}{k}$ на $\binom{i}{k-1}$ ;
Записываем биномиальный коэффициент с учетом уже использованных степеней двойки: $binomials[k] = val \cdot 2^{-(i-2k+2)}$ ;
Вычисляем текущую сумму: ;
Повторяем 6–9

Удобно сделать отдельный класс, который при инициализации будет считать коэффициенты (точнее, вероятности), а потом по запросу выдавать, в зависимости от того, из какой половины — посчитанной или симметричной — требуется коэффициент:

class Binom {
        vector binomials;
        vector sums;
        int i;

    public:
        Binom(int _i) : i(_i), binomials(_i/2 + 1), sums(_i/2 + 1, 0) {
            double val = 1.;

            binomials.front() = val*exp2(-i);
            sums.front() = binomials.front();
            for (int k = 1; k < binomials.size(); k++) {
                val *= (i-k+1.) / k;
                binomials[k] = val*exp2(-(i-2*k+2));
                sums[k] = sums[k-1] + binomials[k];
                val /= 4;
            }
        }

        double get_k(size_t k) {
            if (k < 0) return 0.;
            if (k < binomials.size()) return binomials[k];
            if (k <= i) return binomials[i - k];
            return 0;
        }

        double get_sum(int k) {
            if (k < 0) return 0.;
            if (k < sums.size()) return sums[k];
            if (k < i) return 1. - sums[i - k - 1];
            return 1.;
        }
    };

Отметим, что здесь мы возвращаем коэффициент 0, если выходит за допустимые пределы, что сделает подсчет сумм удобнее. Сумма, соответственно, 0 для k<0 , 1 для $k \ge i$ , но это добавили просто для согласованности, реально таких значений не будет.

Наконец, начинаем считать. Только предварительно переобозначим индекс суммирования $q \rightarrow q+1$ в выражении для P[i,1] . Вместо:

$P[i,1]=2^{-2i}\sum_{q=1}^{\lfloor (i+1)/2 \rfloor} \left[ \binom{i}{q} \binom{i}{2q-1} \right]$

напишем:

$P[i,1]=2^{-2i}\sum_{q=0}^{\lfloor (i-1)/2 \rfloor} \left[ \binom{i}{q+1} \binom{i}{2q+1} \right]$

И суммировать все выражения будем до $\lfloor i/2 \rfloor$ , все равно для неправильных значений коэффициенты будут 0.

Да, вы ведь еще помните, что $2^{-i}\sum_{j=0}^{i}\binom{i}{k}=1$ ?

Алгоритм №2.2. O (n)/O (n)

Находим начальное $s0= \lceil n/25 \rceil$ ;