Стэн Драпкин. Ловушки высокоуровневой криптографии в .NET
Стэн Драпкин — эксперт по безопасности и комплаенсу, имеющий более чем 16 лет опыта работы с .NET Framework (начиная с .NET 1.0-beta в 2001 году). К сожалению, сам он не пишет статьи на русском языке, поэтому мы договорились с ним выпустить перевод его доклада с DotNext Piter. Этот доклад занял первое место на конференции!
Симметричная криптография, ассиметричная, гибридная, высокоуровневая, низкоуровневая, потоковая и современная эллиптическая криптография. Пятьдесят шесть минут видео про криптографию, и гораздо быстрей — в виде текста.

Под катом — видео, слайды и перевод. Приятного прочтения!
Слайды
Меня зовут Стэн Драпкин, я технический директор фирмы, специализирующейся на информационной безопасности и нормативно-правовом соответствии. Кроме того, я — автор нескольких опенсорсных библиотек, весьма неплохо принятых сообществом. Кто из вас слышал об Inferno? В этой библиотеке продемонстрирован правильный подход к криптографии в .NET, а в TinyORM реализован микро-ORM для .NET. Кроме того, я написал несколько книг, которые могут иметь отношение к теме сегодняшней статьи. Одна из них, 2014 года издания — «Security Driven .NET», другая, 2017 года — «Application Security in .NET, Succinctly».
Вначале мы поговорим о том, что я называю четырьмя стадиями крипто-просветления. Затем последуют две основные темы, в первой речь пойдет о симметричной криптографии, во второй — об асимметричной и гибридной. В первой части мы сравним высокоуровневую и низкоуровневую криптографию и взглянем на пример потоковой криптографии (streaming cryptography). Во второй части нас ожидает множество «приключений» с RSA, после чего мы познакомимся с современной эллиптической криптографией.
Итак, как выглядят эти стадии крипто-просветления? Первая стадия — «XOR такой классный, смотри, мама, как я могу!» Наверняка многие из вас с этой стадией знакомы и знают о чудесах функции XOR. Но, я надеюсь, большинство эту стадию переросло и перешло на следующую, то есть научилось выполнять шифрование и дешифрование при помощи AES (Advanced Encryption Standard), широко известного и высоко оцененного алгоритма. Большинство разработчиков, не посещающих DotNext, находится именно на этой стадии. Но, коль скоро вы следите за DotNext и знакомы с докладами об опасностях низкоуровневых API, вы, скорее всего, находитесь на следующей стадии — «я всё делал (а) неправильно, нужно переходить на высокоуровневые API». Ну, и для полноты картины я упомяну также последнюю стадию — понимание того, что при наилучшем решении проблемы криптография может быть и вовсе не нужна. Дойти до этой стадии сложнее всего, и людей на ней находится немного. В качестве примера можно привести Питера Ньюмана (Peter G. Neumann), который сказал следующее: «Если вы считаете, что решение вашей проблемы кроется в криптографии, то вы не понимаете, в чем именно состоит ваша проблема».
О том, что низкоуровневая криптография опасна, говорилось уже на многих докладах о .NET. Можно сослаться на доклад Владимира Кочеткова 2015 года, «Подводные камни System.Security.Cryptography». Основная его мысль в том, что на каждом этапе работы с низкоуровневыми криптографическими API мы, сами того не зная, принимаем множество решений, для многих из которых у нас просто нет соответствующих знаний. Основной вывод — в идеале вместо низкоуровневой криптографии следует использовать высокоуровневую. Это замечательный вывод, но он приводит нас к другой проблеме — знаем ли мы, как именно должна выглядеть высокоуровневая криптография? Давайте немного поговорим об этом.
Определим признаки не-высокоуровневого криптографического API. Для начала, такой API не будет производить впечатление родного для .NET, скорее он будет похож на низкоуровневую оболочку. Далее, такой API легко будет использовать неправильно, т.е. не так, как следует. Кроме того, он будет заставлять вас генерировать множество странных низкоуровневых вещей — nonce-ов, векторов инициализации и тому подобного. Такой API будет вынуждать вас принимать неприятные решения, к которым вы можете быть не готовы — выбирать алгоритмы, режимы дополнения (padding modes), размеры ключей, nonce-ы и так далее. У него также не будет правильного API для потоков (streaming API) — о том, как последний должен выглядеть, мы еще поговорим.
В противоположность этому, как должен выглядеть высокоуровневый криптографический API? Я считаю, что он в первую очередь должен быть интуитивно понятным и лаконичным как для читающего код, так и для пишущего его. Далее, такой API должен быть прост в освоении и использовании, и его должно быть крайне сложно применить неверным образом. Он также должен быть мощным, то есть должен позволять нам достигать нашей цели ценой небольших усилий, небольшого количества кода. Наконец, у такого API не должно быть длинного списка ограничений, предостережений, особых случаев, в целом — должен быть минимум вещей, о которых необходимо помнить при работе с ним, иначе говоря — он должен характеризоваться низким уровнем помех (low-friction), должен просто работать безо всяких оговорок.
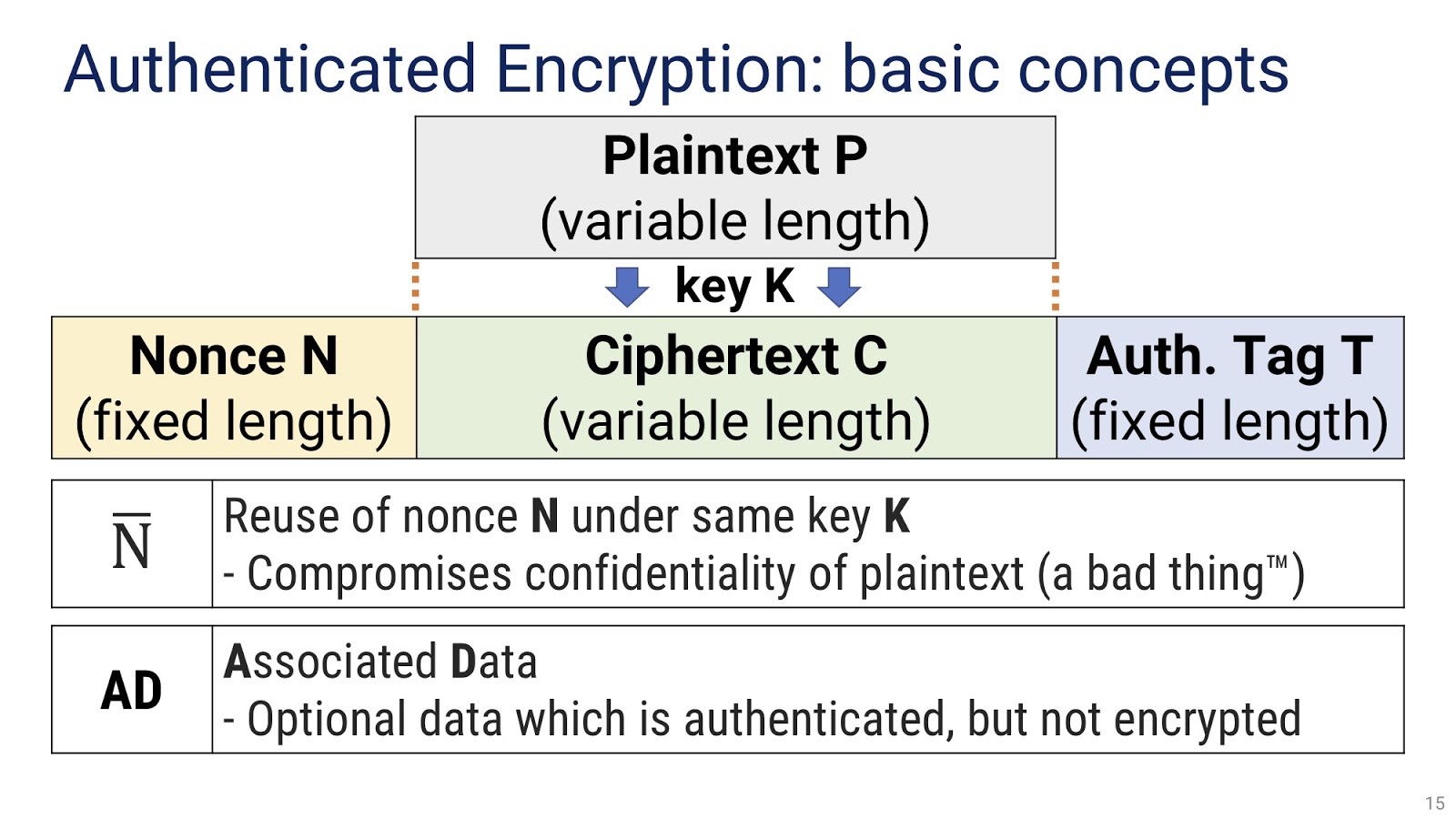
Разобравшись с требованиями к высокоуровневому криптографическому API для .NET, как нам его теперь найти? Можно попробовать просто загуглить, но это было бы слишком примитивно — мы с вами профессиональные разработчики, и это не наш метод. Поэтому мы исследуем эту проблему и опробуем различные альтернативные варианты. Но для этого нам надо вначале составить для себя правильное представление о том, что такое аутентифицированное шифрование (Authenticated Encryption), а для этого необходимо разобраться с основными понятиями. Они следующие: открытый текст P (plaintext), который мы преобразуем в шифротекст C (ciphertext) той же длины при помощи некоторого секретного ключа K (key). Как видим, пока что мы работаем с очень простой схемой. Кроме того, у нас также есть тег аутентификации T и nonce N. Важным параметром является N̅, то есть повторное использование nonce-ов с одним ключом. Как многие из вас, наверное, знают, оно ведет к нарушению конфиденциальности текста, что, очевидно, нежелательно. Другое важное понятие — AD (Associated Data), то есть ассоциированные данные. Это необязательные данные, которые аутентифицированы, но не участвуют в шифровании и дешифровании.
Разобравшись с основными понятиями, взглянем на различные варианты криптографических библиотек для .NET. Начнем с анализа Libsodium.NET. Кто из вас знаком с ней? Как вижу, некоторые знакомы.
nonce = SecretAeadAes.GenerateNonce();
c = SecretAeadAes.Encrypt(p, nonce, key, ad);
d = SecretAeadAes.Decrypt(c, nonce, key, ad);
Перед вами код на C#, при помощи которого выполняется шифрование с Libsodium.NET. На первый взгляд он достаточно прост и лаконичен: в первой строке генерируется nonce, который затем используется во второй строке, где происходит собственно шифрование, и в третьей, где текст расшифровывается. Казалось — какие тут могут быть сложности? Для начала, в Libsodium.NET предлагаются не один, а три различных метода симметричного шифрования:
Раз
nonce = SecretAeadAes.GenerateNonce();
c = SecretAeadAes.Encrypt(p, nonce, key, ad);
d = SecretAeadAes.Decrypt(c, nonce, key, ad);
Два
nonce = SecretAead.GenerateNonce();
c = SecretAead.Encrypt(p, nonce, key, ad);
d = SecretAead.Decrypt(c, nonce, key. ad);
Три
nonce = SecretBox.GenerateNonce();
c = SecretBox.Create(p, nonce, key);
d = SecretBox.Open(c, nonce, key);
Очевидно, встает вопрос — который из них лучше в вашей конкретной ситуации? Чтобы на него ответить, необходимо залезть внутрь этих методов, что мы сейчас и сделаем.
Первый метод, SecretAeadAes, использует AES-GCM с 96-битным nonce-ом. Важно, что у него достаточно длинный список ограничений. К примеру, при использовании него не следует шифровать больше 550 гигабайт одним ключом, и не должно быть больше 64 гигабайт в одном сообщении при максимуме в 232 сообщений. Причем библиотека не предупреждает о приближении к этим ограничениям, отслеживать их необходимо вам самостоятельно, что создает дополнительную нагрузку на вас как на разработчика.
Второй метод, SecretAead использует другой комплект шифров, ChaCha20/Poly1305 со значительно меньшим, 64-битным nonce-ом. Такой маленький nonce делает коллизии крайне вероятными, и уже только на этом основании этим методом не стоит пользоваться — за исключением достаточно редких случаев и при условии, что вы очень хорошо разбираетесь в теме.
Наконец, третий метод, SecretBox. Здесь нужно сразу заметить, что в аргументах для этого API отсутствуют ассоциированные данные. Если вам необходимо аутентифицированное шифрование с AD, этот метод вам не подойдет. Алгоритм шифрования, используемый здесь, называется xSalsa20/Poly1305, nonce достаточно большой — 192 бита. Все же, отсутствие AD является существенным ограничением.
При использовании Libsodium.NET возникают некоторые вопросы. Например, что именно мы должны сделать с nonce-ом, генерируемым первой строкой кода в приведенных выше примерах? Библиотека ничего нам об этом не говорит, разобраться в этом нам предстоит самостоятельно. Скорее всего, мы будем вручную добавлять этот nonce в начало или в конец шифротекста. Далее, у нас могло сложиться впечатление, что AD в первых двух методах могут быть любой длины. Но на самом деле библиотека поддерживает AD длиной не более 16 байт — ведь 16 байт хватит на всех, правда? Идём дальше. Что происходит при ошибках дешифрования? В данной библиотеке было принято решение в этих случаях бросать исключения. Если в вашей среде при раcшифровке может быть нарушена целостность данных, то у вас будет возникать множество исключений, которые нужно будет обрабатывать. Что делать, если размер вашего ключа не равен в точности 32 байтам? Библиотека ничего нам об этом не сообщает, это ваши проблемы, которые её не интересуют. Другая важная тема — повторное использование массивов байтов с целью уменьшить нагрузку на сборщик мусора в интенсивных сценариях. Например, в коде мы видели массив который нам вернул генератор nonce-ов. Хотелось бы не создавать каждый раз новый буфер, а переиспользовать существующий. В данной библиотеке это невозможно, массив байтов будет каждый раз генерироваться заново.
Используя уже виденную нами схему, попробуем сравнить различные алгоритмы Libsodium.NET.

Первый алгоритм — AES-GCM, использует nonce длиной в 96 бит (жёлтый столбец на картинке). Он меньше 128 бит, что создаёт некоторый дискомфорт, но не слишком существенный. Следующий столбец — синий, это место, занимаемое тегом аутентификации, у AES-GCM оно равно 16 байт или 128 бит. Вторая синяя цифра, в скобках, означает количество энтропии, или случайности, содержащееся в этом теге — меньше 128 бит. Насколько меньше — в данном алгоритме зависит от того, какой объём данных шифруется. Чем больше шифруется, тем тег становится слабее. Уже это должно породить у нас сомнения в данном алгоритме, которые только усилятся, если мы взглянем на белый столбец. Там написано, что повторы (коллизии) nonce-ов приведут к подделке всех шифротекстов, созданных тем же самым ключом. Если из, скажем, 100 ваших шифротекстов созданных общим ключом в двух есть коллизия nonce-а, этот nonce приведёт к внутренней утечке ключа аутентификации и позволит злоумышленнику подделать любой другой шифротекст, созданный данным ключом. Это весьма существенное ограничение.
Перейдём ко второму методу Libsodium.NET. Как я уже говорил, здесь для nonce-а используется слишком небольшое пространство, всего 64 бита. Тег занимает 128 бит, но содержит только 106 бит энтропии или меньше, иначе говоря, существенно ниже уровня безопасности в 128 бит, которого в большинстве случаев пытаются достичь. Что касается подделывания, то здесь ситуация несколько лучше, чем в случае с AES-GCM. Коллизия nonce-ов приводит к подделке шифротекстов, но только для тех блоков, в которых коллизии произошли. В предыдущем примере у нас оказались бы подделанными 2 шифротекста, а не 100.
Наконец, в случае с алгоритмом xSalsa/Poly мы имеем очень большой nonce размером в 192 бита, благодаря чему коллизии оказываются крайне маловероятными. Способ аутентификации здесь тот же, что и в прошлом методе, поэтому тег опять-таки занимает 128 бит и имеет 106 бит энтропии или меньше.
Сравним все эти цифры с соответствующими показателями библиотеки Inferno. В ней nonce занимает колоссальное пространство, 320 бит, что делает коллизии практически невозможными. Что касается тега, то с ним в ней всё просто: он занимает ровно 128 бит и имеет ровно 128 бит энтропии, не меньше. Это — пример надёжного и безопасного подхода.
Прежде, чем более подробно знакомиться с Libsodium.NET, нам надо понять его предназначение — к сожалению, его осознают далеко не все, кто пользуется этой библиотекой. Для этого необходимо обратиться к её документации, в которой указано, что Libsodium.NET является оберткой на С# для libsodium. Это другой опенсорсный проект, в документации которого написано, что он является форком NaCl с совместимым API. Что же, обращаемся к документации NaCl, еще одного опенсорсного проекта. В ней в качестве цели NaCl постулируется предоставить все необходимые операции для создания высокоуровневых криптографических инструментов. Именно здесь зарыта собака: задачей NaCl и всех его оболочек является предоставить низкоуровневые элементы, из которых затем кто-то другой уже сможет собрать высокоуровневые криптографические API. Сами эти оболочки как высокоуровневые библиотеки не задумывались. Отсюда мораль: если вам необходим высокоуровневый криптографический API, вам надо найти высокоуровневую библиотеку, а не пользоваться низкоуровневой оберткой и делать вид, что работаете с высокоуровневой.
Рассмотрим, как работает шифрование в Inferno.

Перед вами пример кода, в котором, как и в случае с Libsodium, каждое шифрование и дешифрование занимает всего одну строчку. В качестве аргументов используется ключ, текст и необязательные ассоциированные данные. Следует обратить внимание, что здесь нет nonce-ов, нет необходимости принимать какие-либо решения, в случае ошибки дешифрования просто возвращается null, без всякого бросания исключений. Поскольку создание исключений существенно увеличивает нагрузку на сборщик мусора, их отсутствие весьма важно для сценариев с обработкой больших потоков данных. Надеюсь, мне удалось вас убедить в том, что такой подход является оптимальным.
Из интереса давайте попробуем зашифровать какую-нибудь строку. Это должен быть наиболее простой сценарий, реализовать который могут все. Предположим, что у нас возможны только два различных значения строки: «LEFT» и «RIGHT».

На картинке вы видите шифрование этих строк при помощи Inferno (хотя для данного примера не важно, какая именно библиотека используется). Мы шифруем две строки одним ключом и получаем два шифротекста, c1 и c2. Всё ли в этом коде верно? Является ли он готовым к продакшну? Кто-то может сказать, что возможна проблема в коротком ключе, но она далеко не главная, так что будем считать, что ключ используется один и тот же, и он достаточной длины. Я имею в виду нечто иное: при обычных криптографических подходах c1 в нашем примере будет короче c2. Это называется length leaking («утечка по длине») — c2 во многих случаях будет на один байт длиннее c1. Это может позволить злоумышленнику понять, какая именно строка представлена данным шифротекстом, «LEFT» или «RIGHT». Проще всего решить эту проблему можно, если сделать так, чтобы обе строки имели одинаковую длину — например, добавить символ в конец строки «LEFT».
На первый взгляд length leaking воспринимается как несколько надуманная проблема, которая в реальных приложениях встретиться не может. Но в январе 2018 года в журнале Wired вышла статья с исследованием, осуществленным израильской компанией Checkmarx, под заголовком «Отсутствие шифрования в Tinder позволяет посторонним отслеживать, когда вы проводите по экрану». Я коротко перескажу содержание, но сначала грубое описание функционала Tinder. Tinder — это приложение, которое получает поток с фотографиями, и затем пользователь проводит по экрану направо или налево, в зависимости от того, нравится ему фото или нет. Исследователи обнаружили, что, хотя сами команды были правильно зашифрованы с использованием TLS и HTTPS, данные команд для проведения направо занимали иное количество байт, чем данные для проведения налево. Это, конечно, уязвимость, но сама по себе она не слишком существенная. Более существенным для Tinder был тот факт, что сами потоки с фотографиями они отправляли через обычный HTTP, без всякого шифрования. Так что злоумышленник мог получить доступ не только к реакциям пользователей на фотографии, но и к самим фотографиям. Так что, как видим, length leaking является вполне реальной проблемой.
Попробуем теперь зашифровать файл. Сразу же нужно сказать, что в Libsodium.NET шифрование файлов или, шире, шифрование потоков, по умолчанию не реализовано, там это приходится делать вручную — что, поверьте мне, правильно сделать очень сложно. В Inferno дела с этим обстоят гораздо лучше.

Выше вы видите пример, взятый практически без изменений из MSDN. Он очень простой, здесь мы видим один поток для исходного файла и другой для файла назначения, а также криптопоток, который преобразует первый во второй. В этом коде Inferno используется только в одной строчке — в той, где происходит преобразование. Итак, перед нами простое и в то же время полностью работающее и проверенное решение для шифрования потока.
Следует помнить, что при шифровании одним и тем же ключом у нас существует ограничение на количество сообщений. Они существуют и в Inferno, причём в этой библиотеке они ясно прописаны на экране. Но в то же время в Inferno они настолько велики, что на практике вы их никогда не достигнете. В Libsodium.NET ограничения разные для разных алгоритмов, но во всех случаях они достаточно низкие, чтобы их превышение было вероятным. Так что необходимо проверять, будут ли они достигнуты в каждом отдельном сценарии.
Нам также следует поговорить об аутентификации ассоциированных данных, поскольку это тема, которая освещается не часто. AD могут быть «слабыми»: это значит, что они проходят аутентификацию, но в самом процессе шифрования и дешифрования никак не участвуют. Напротив, «сильные» AD изменяют сам этот процесс. В большинстве известных мне библиотек AD слабые, в то время как в Inferno используется второй подход, там AD используются в самом процессе шифрования/дешифрования…
Следует также остановиться на том, к какому уровню безопасности должна стремиться высокоуровневая криптография. Если коротко, мой ответ такой: 256-битное шифрование со 128-битным тегом аутентификации. Почему необходим настолько большой ключ? Тому есть множество причин, каждая из которых значима сама по себе, но сейчас мне хотелось бы, чтобы вы запомнили одну: нам необходимо предохраниться от возможных предвзятостей (bias) при генерировании криптографических ключей. Поясню, что имеется ввиду под предвзятостью. У генератора случайных битов без предвзятостей для каждого бита вероятности принять значение 0 или 1 равны. Но предположим, что у нашего генератора бит будет принимать значение 1 с вероятностью 56%, а не 50%. На первый взгляд, эта предвзятость небольшая, но на самом деле она значительна: 25%. Попробуем теперь подсчитать, сколько энтропии мы получим при генерировании определённого количества бит нашим генератором.

На картинке вы видите формулу, по которой будет производиться этот расчёт. Важно, что в ней только две переменных: предвзятость, о которой мы уже говорили (bias), и количество бит, создаваемое генератором. Будем считать, что предвзятость равна 25% — это достаточно экстремальный случай, на практике вы, скорее всего не будете работать в системах с настолько искажённым генератором случайных чисел. Как бы то ни было, при 25% предвзятости и 128-битном ключе мы получим всего 53 бита энтропии. Во-первых, это существенно меньше 128 бит, которые обычно ожидаются от генератора случайных чисел, во-вторых, при современных технологиях такой ключ можно просто брутфорсить. Но если вместо 128-битного ключа мы используем 256-битный, то получаем 106 бит энтропии. Это уже весьма неплохо, хоть и меньше ожидаемых 256. С современными технологиями взломать такой ключ практически невозможно.
В завершение первой части доклада подведу промежуточные итоги. Я рекомендую всем пользоваться хорошо написанными криптографическими API. Найдите тот, который вас устроит, или отправьте петицию в Microsoft, чтобы они вам его написали. Кроме того, при выборе API следует обращать внимание на наличие поддержки работы с потоками. По уже объяснённым причинам минимальная длина ключа должна быть 256 бит. Наконец, следует иметь в виду, что высокоуровневая криптография, как и любая другая, не идеальна. Утечки могут происходить, и в большинстве сценариев об их возможности необходимо помнить.
Давайте теперь поговорим об ассиметричной, или гибридной криптографии. Поставлю вопрос с подвохом: умеете ли вы пользоваться RSA в .NET? Не торопитесь отвечать утвердительно, как это делают многие — давайте сначала проверим ваши знания в этой области. Следующие слайды будут специально предназначены для людей, уже знакомых с этой темой. Но вначале обратимся к википедии, и вспомним, чем именно является RSA — на случай, если кто-то забыл или давно не пользовался этим алгоритмом.

Предположим, существует некоторая Алиса, которая при помощи генератора случайных чисел создает пару ключей, в которую входит один частный и один публичный. Далее, существует некоторый Боб, который хочет зашифровать сообщение для Алисы: «Привет, Алиса!» При помощи её публичного ключа он генерирует шифротекст, который затем отправляет ей. Расшифровывает она этот шифротекст с помощью частной части своего ключа.
Попробуем воспроизвести этот сценарий на практике.

Как видно выше, мы создаём экземпляр RSA и зашифровываем некоторый текст. Сразу же обращаем внимание, что .NET заставляет нас выбрать режим дополнения (padding mode). Их существует пять, все с непонятными именами. Если мы попробуем их все по очереди, то выясним, что последние три попросту бросают исключение и не работают. Воспользуемся одним из двух оставшихся — OaepSHA1. Здесь ключ будет размером в 1 килобит, что слишком мало для RSA, это практически взломанный ключ. Поэтому нам придётся выставить размер ключа вручную. Из документации мы узнаём, что есть специальное свойство .KeySize, которое получает или задаёт размер ключа.

На первый взгляд это ровно то, что нам необходимо, поэтому мы пишем: rsa.KeySize = 3072. Но если, руководствуясь смутным подозрением, мы после этого проверим, чему теперь равен размер ключа, то узнаем, что он по-прежнему занимает 1 килобит. Не важно, будем мы проверять этот параметр при помощи метода WriteLine(rsa.KeySize), или rsa.ExportParameters(false).Modulus.Length * 8 — в последнем случае экспортируется публичный компонент ключа RSA, для этого нужен аргумент «false». Modulus этого ключа является массивом, который мы умножаем на 8 и получаем размер в битах — который опять-таки будет 1 килобит. Как видим, этот алгоритм отправлять в продакшн ещё рановато.
Не будем тратить время на выяснение того, почему этот API не работает, вместо этого попробуем другую реализацию RSA, предоставленную Microsoft в .NET 4.6, то есть совсем новую. Она называется RSACng, причём Cng расшифровывается как Cryptography next generation («следующее поколение криптографии»). Великолепно, кто же не хочет работать с инструментами следующего поколения? Наверняка здесь мы найдем волшебное решение всех наших проблем.

Мы запрашиваем экземпляр RSACng, вновь задаём размер ключа в 3 килобита, вновь проверяем размер ключа через WriteLine(rsa.KeySize) — и вновь узнаём, что размер ключа по-прежнему равен одному килобиту. Вдобавок, если мы запросим тип объекта, сгенерировавшего ключ — как помним, мы запросили экземпляр RSACng — то узнаем, что это RSACryptoServiceProvider. Я просто хочу поделиться здесь моим личным ощущением отчаяния, и завопить: «За что, Microsoft?!».
После длительных терзаний и мучений, мы выясняем, что пользоваться на самом деле нужно конструктором, а не фабрикой.

Здесь значение размера ключа по умолчанию 2048 бит, что уже значительно лучше. Что ещё лучше — здесь нам удаётся, наконец, задать размер ключа в 3 килобита. Как говорится, achievement unlocked.
Напомню, что все наши старания до сих пор сводились только к созданию RSA, к шифрованию мы ещё даже не приступали. По-прежнему остаются вопросы, на которые нам предварительно нужно ответить. Для начала, в какой степени можно полагаться на размеры ключей по умолчанию? Реализация фабрики RSA может быть переопределена в machine.config, следовательно, она может измениться без вашего ведома (например, её может поменять системный администратор). А это значит, что может поменяться и размер ключа по умолчанию. Таким образом, вы никогда не должны доверять значениям, предоставляемым по умолчанию, размер ключа всегда нужно выставлять самостоятельно. Далее, насколько хороши предоставляемые по умолчанию размеры ключей RSA? В .NET существует две реализации RSA, одна на основе RSACryptoServiceProvider, другая на основе RSACng. В первой размер по умолчанию 1 килобит, во второй два. Давайте из интереса сравним эти значения с имеющимися в сети Bitcoin (BCN). Я заранее извиняюсь за поднятие больной темы, но мы не будем обсуждать Bitcoin или криптовалюту, речь пойдёт только о самой сети. У неё есть публикуемый hashrate, который растёт с каждым месяцем и на сегодняшний день равен 264 хэшам в секунду. Это эквивалентно 290 хэшам в год. Предположим для простоты, что хэш является эквивалентом базовой операции — хоть это и не вполне верно, он более сложен. Если вы читаете книги по криптографии, написанные действительными профессионалами, а не людьми вроде меня, то вы знаете, что 270 операций (то есть одной минуты BCN) достаточно, чтобы взломать 1-килобитный ключ RSA, а 290 (одного года BCN) — чтобы взломать 2-килобитный ключ. Оба значения должны вызывать у нас тревогу — это то, чего можно достичь при уже существующих технологиях. Именно поэтому я настоятельно рекомендую всегда самостоятельно задавать размер ключа, и делать его по меньшей мере размером в 3 килобита, а если вам позволяет производительность — то и 4.
В .NET не так просто разобраться, как экспортировать публичные и частные ключи.

В верхней части слайда вы видите два экземпляра ключа RSA, первый от RSACryptoServiceProvider, второй от RSACng, каждый по 4 килобита. Ниже показан код, при помощи которого извлекается публичный и частный ключ из обоих экземпляров. Здесь следует обратить внимание на то, что оба API достаточно сильно отличаются друг от друга — разный код, разные методы, разные параметры. Далее, если мы сравним размеры публичных ключей у первого и второго экземпляра, то увидим, что они сравнимы, примерно по полкилобайта каждый. Но вот частный ключ у новой реализации RSA значительно меньше, чем у старой. Это необходимо иметь ввиду и соблюдать единообразие, не мешать эти два API друг с другом.
Всё, что мы делали с RSA до сих пор, сводилось к попыткам получить рабочий экземпляр; теперь попробуем что-нибудь зашифровать.

Создадим массив байтов, который будет нашим открытым текстом (data), а затем зашифруем его при помощи одного из тех режимов дополнения, которые не бросали исключение. Но на этот раз исключение у нас возникнет. Это исключение неверного параметра;, но о каком параметре идёт речь? Я понятия не имею — и Microsoft, скорее всего, тоже. Если мы попробуем запустить тот же метод с другими режимами дополнения, то в каждом случае получим то же исключение. Так что дело не в режиме дополнения. Значит, проблема в самом исходном тексте. Сложно сказать, что именно с ним неверно, так что попробуем на всякий случай урезать его в два раза. На этот раз шифрование проходит успешно. Мы остаёмся в недоумении.
Возможно, всё дело в том, что мы использовали дополнение SHA-1? SHA-1, как мы знаем, уже не является криптографически-сильной функцией, поэтому наши аудиторы и отдел нормативно-правового соответствия (compliance department) настаивают на том, чтобы мы от неё избавились. Заменим OaepSHA1 на OaepSHA256, по меньшей мере это успокоит аудиторов.

Но при попытке шифрования мы вновь получим исключение неверного параметра. Вся эта ситуация вызвана тем, что ограничение на размер текста, который можно передать криптографической функции, зависит не только от режима дополнения, но и от размера ключа.
Попытаемся выяснить, как именно выглядит та волшебная формула, которая определяет максимальный объём шифруемых данных. Она должна находиться в методе int GetMaxDataSizeForEnc(RSAEncryptionPadding pad), который рассчитывает этот объём, получив на вход режим дополнения. Главный недостаток этого метода заключается в том, что он не существует, я его выдумал. Я пытаюсь донести мысль о том, что даже самая основная информация, необходимая разработчику для правильного использования RSA, нам недоступна. Спасибо, Microsoft.
Приведу причины, по которым RSA следует избегать, даже для подписи. Как, я надеюсь, мне удалось показать, API для RSA в .NET крайне неудовлетворительны. Вас заставляют принимать множество решений относительно режима дополнения, размера данных и тому подобного, что нежелательно. Далее, для 128-битного уровня безопасности вам понадобится по меньшей мере весьма громоздкий 4-килобитный ключ. Он даст вам частный ключ размером в килобайт, публичный ключ размером в пол-килобайта, и сигнатуру размером в пол-килобайта. Для многих сценариев такие значения могут быть нежелательны. А если вы попытаетесь достичь 256-битного уровня безопасности, вам понадобится и вовсе огромный ключ — 15360 бит. В RSA использование подобного ключа практически невозможно. На моём ноутбуке один такой ключ генерируется полторы минуты. В дополнение к этому RSA на фундаментальном уровне, как алгоритм, весьма медленно осуществляет подпись, независимо от реализации. Почему нам важна скорость подписи? Если вы используете TLS с сертификатами RSA, то подпись осуществляется на сервере. А нас, как разработчиков, в наибольшей степени касается именно то, что происходит на сервере, мы за него ответственны, нам важна его пропускная способность. Резюмируя, я хочу ещё раз порекомендовать не пользоваться RSA.
В таком случае, чем заменить RSA? Я хотел бы познакомить вас с современными эллиптическими криптографическими примитивами. В первую очередь вам следует иметь ввиду алгоритм ECDSA (Digital Signature Algorithm, «алгоритм цифровой подписи»), который можно использовать вместо RSA для подписей. В этой и следующих аббревиатурах EC — общий префикс, который расшифровывается как Elliptic-Curve («эллиптический»). По ссылке securitydriven.net/inferno/#DSA Signatures можно найти пример кода ECDSA, который, кстати говоря, является родным для .NET. Другой важный алгоритм — ECIES (Integrated Encryption Scheme, «эллиптическая интегрированная схема шифрования»). Этот алгоритм может выполнять гибридное шифрование вместо RSA, то есть такое, где вы генерируете симметричный ключ, шифруете ими данные и затем шифруете сам ключ. Пример кода доступен по ссылке securitydriven.net/inferno/#ECIES example. Наконец, ещё один очень важный алгоритм — ECDH (Diffie-Hellman key exchange, «обмен ключей Диффи-Хеллмана»). Он позволяет создавать ключи для симметричного шифрования между двумя сторонами с известными публичными ключами. В некоторых ситуациях и способах использования он позволяет добиться прямой секретности (forward secrecy). По ссылке securitydriven.net/inferno/#DHM Key Exchange доступен пример кода.
Подведём итоги разговору об асимметричном шифровании. Всегда следует пользоваться высокоуровневыми API, не заставляющими вас принимать решения, к которым вы не готовы. Я также рекомендовал бы перестать пользоваться RSA. Конечно, это проще сказать, чем сделать, поскольку мы все работаем с большими уже созданными приложениями, провести полный рефакторинг которых может быть невозможно. В этом случае по меньшей мере необходимо научиться правильно использовать RSA. Далее, я советую познакомиться с современными эллиптическими криптографическими алгоритмами (ECDSA, ECDH, ECIES). Наконец, важно, что высокоуровневая криптография не решает волшебным образом все проблемы, поэтому необходимо помнить о целях, которые вы преследуете. Приведу цитату со StackOverflow, с которой я полностью согласен: «Криптография сама по себе не решает проблем. Симметричное шифрование только превращает проблему конфиденциальности данных в проблему управления ключами».
Скажу пару слов о ресурсах, которые, возможно, будут вам полезны. Существует относительно приемлемая высокоуровневая библиоте
