Статистика Backblaze, научный подход к анализу надёжности накопителей
Фирма Backblaze регулярно публикует статистику по отказам своих жёстких дисков, и даже выложила в свободный доступ полный архов со статистикой S.M. A.R.T параметров всех своих накопителей.
В этой статье я покажу как с помощью при помощи лома и какой-то матери с помощью научных методов рассчитывать надёжность накопителей.
Анализ выживаемости
В статистике, анализом выживаемости или надёжности занимается раздел под названием «survival analysis».
В кратце, это набор методов позволяющих сравнивать и рассчитывать как различные факторы влияют на продолжительность жизни (в медицине), времени наработки на отказ (в механике) и т.д. В общем случае, это анализ времени до наступления некоторого события. Т.е ответить на вопрос, типа: «какова будет доля выживших среди пациентов спустя некоторое время после применённых техник лечения?» или «какой процент накопителей выйдет из строя в следующем году?».
При этом, ответы на такие вопросы надо искать когда время наблюдения за состоянием больных (или накопителей) ограничено и не возможно определить время жизни всех пациентов.
Термины
- «Событие» — смерть пациента, первая поломка и т.д, время до которого мы можем или хотим измерить
- «Время» — собственно время от начала наблюдения до наступления события, либо до того момента когда мы не способны продолжать наблюдение (пациент уехал, накопитель отключили, и т.д)
- «Цензурирование» — прекращение наблюдения за пациентом до наступления «События». Не имеет отношения к системе государственного надзора за содержанием и распространением информации.
- «Функция выживания», обычно обозначается как S (t) — вероятность что пациент доживёт до времени t, обычно предполагается что S (0)=100% и с течением времени функция не увеличивается.
- «Функция риска» («Hazard function») — h (t) — вероятность того что пациент умрёт в момент времени t, за единицу времени. Т.е первая производная функции выживания со знаком минус.
Данные
Компания backblaze выложила в открытый доступ базу данных со всеми параметрами S.M. A.R.T всех своих жёстких дисков, в формате .csv разбитую на файлы по дням. Если все эти файлы импортировать в базу данных (они предлагают свои собственные скрипты для импорта в sqlite3) то получится таблица с 90126570 записями, занимает она примерно 19Гб и описывает 122619 накопителей. Я сделал небольшой скрипт, который вытаскивает в одну таблицу следующие данные о каждом накопителе: производитель, модель, серийный номер, ёмкость, дата начала службы, время работы либо до окончания наблюдения (параметр S.M. A.R.T 9), либо до события и признак события. CSV файл с этой информацией можно загрузить тут:
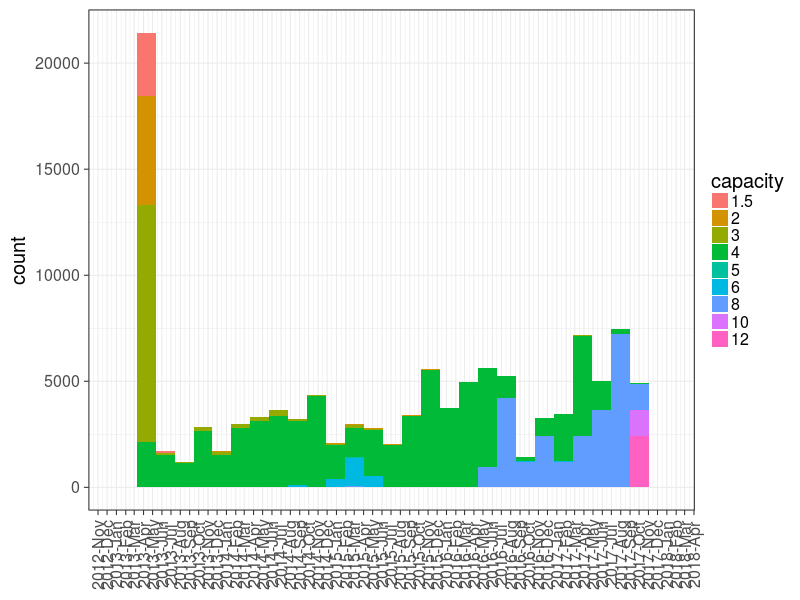
График 0: Распределение накопителей по обьёму и дате вводе в строй.
Статистика
Для обработки буду использовать R с пакетами tidyverse, survival, survminer, zoo
Для начала, пример как принято представлять функцию выживания :
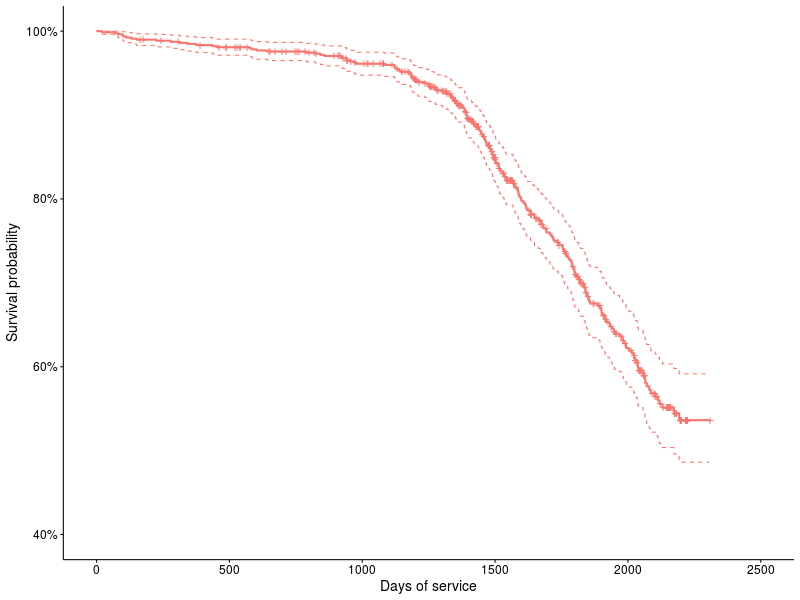
График 1: Функция выживания для накопителя ST31500341AS.
Смотрим на график 1: Это пример графика выживания по методологии Каплана — Мейера, по вертикальной оси отложены проценты выживших устройств, по горизонтальной — количество дней. Крестики показывают отцензурированные устройства (т.е они дожили как минимум до момента X, а дальше следы теряются). Пунктирные линии показывают 95% доверительные интервалы. Методология Каплана — Мейера (K-M) появилась ещё в 58 году и с тех пор активно используется для описания функции выживания, надо заметить что это непараметрический метод, и использует кусочно-линейную функцию для аппроксимации функции выживания (т.е с небольшим количеством данных хорошо видны ступеньки). В пакете survival это делается следующим образом:
survfit(Surv(age_days, status) ~ 1, ...)Где в качестве аргумента сначала идёт формула где слева специальная функция Surv показывает что мы имеем дело с данными и событиях, а потом источник данных: age_days — время, status — код для события (1 — события произошло, 0 — данные отцензурированы). Результат можно красиво нарисовать с помощью survminer.
Метод K-M позволяет сравнивать функции выживания между собой, чтобы определить есть-ли между ними статистически-значимая разница, для примера взял данные о двух моделях накопителей: ST31500341AS и ST31500541AS:
survfit(Surv(age_days, status) ~ model, ...)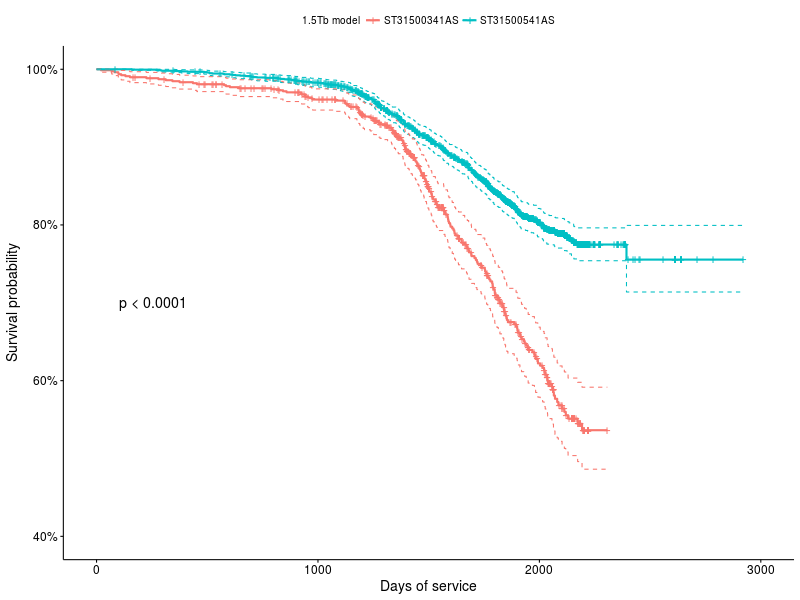
График 2: Функции выживания для накопителей ST31500341AS и ST31500541AS
Для сравнения распределений используем функцию survdiff:
survdiff(Surv(age_days, status) ~ model, ...)
N Observed Expected (O-E)^2/E (O-E)^2/V
model=ST31500341AS 787 216 125 66.4 84.3
model=ST31500541AS 2188 397 488 17.0 84.3
Chisq= 84.3 on 1 degrees of freedom, p= 0 Для нас самое главное — последняя строчка, со значением p, оно показывает вероятность того что распределения не значительно отличаются, в данном случае даже на глаз видно что быть такого не может.
Стоит заметить, что таким способом можно только сказать — есть разница или её нет, т.е не возможно сказать что страта A умирает на XX% быстрее страты Б.
Ещё один интересный график, посмотрим как живучесть самого популярного в backblaze накопителя (ST4000DM000) изменялась со временем установки:
survdiff(Surv(age_days, status) ~ start_quarter, ...)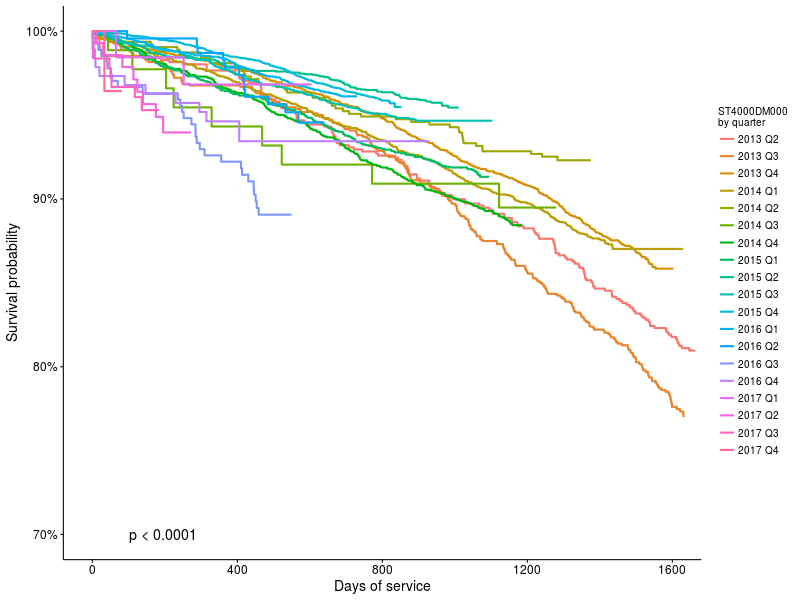
График 3: Функции выживания для накопителей ST4000DM000, в зависимости от даты начала работы.
Видно что разница есть (p<0.0001) но интересно узнать, насколько она большая.
Модель пропорциональных рисков Кокса
И тут нам на помощь приходит модель пропорциональных рисков Кокса, она позволяет оценивать относительные риски между разными стратами, но исходит из предположения что все они отличаются друг-от-друга строго пропорционально.
Для расчета используется функция coxph:
model_coxph<-coxph(Surv(age_days, status) ~ make + capacity + year, ...)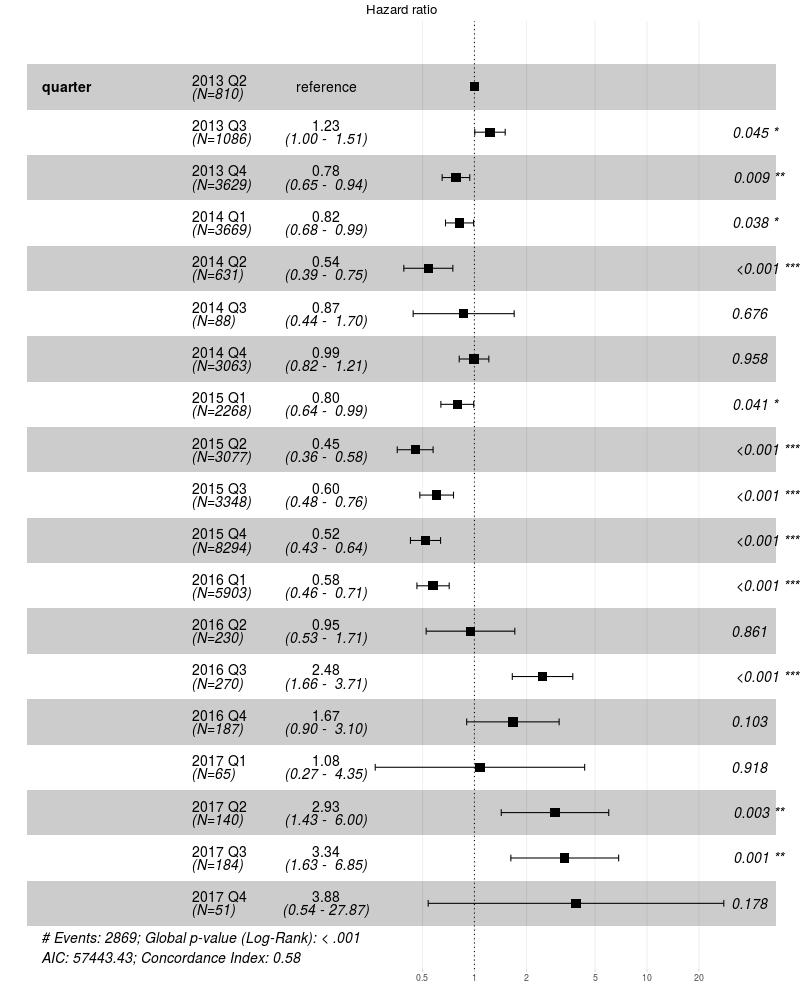
График 4: Относительные коэффициенты риска (т.е скорость умирания) для ST4000DM000 в зависимости от квартала установки. Звёздочки показывают кварталы, когда скорость умирания существенно отличается от базовой (в первом квартале 2013 г).
Теперь сравним 4 самых популярных моделей больших накопителей: 8Тб: ST8000NM0055, ST8000DM002 10Тб ST10000NM0086 и 12Тб ST12000NM0007
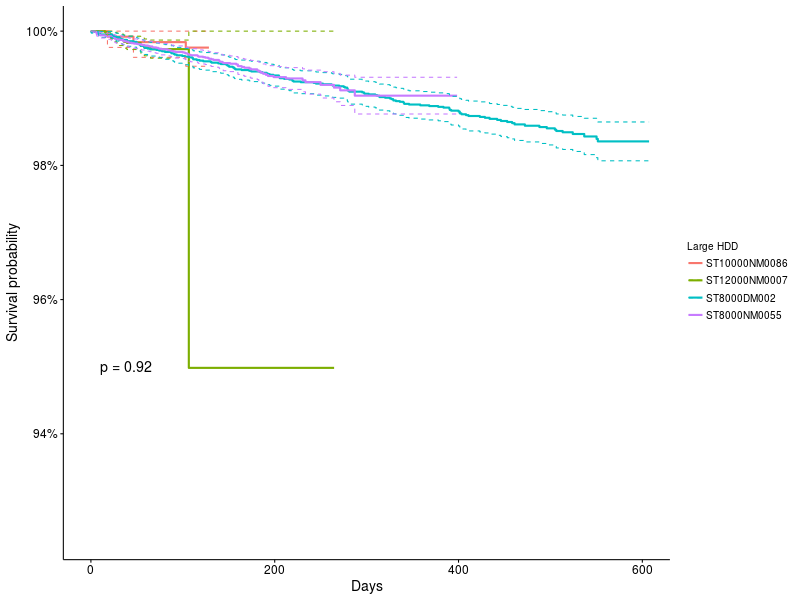
График 5: Функции выживания для больших накопителей.
Метод K-M показывает, что разницы между ними нет, несмотря на странный скачок для модели ST12000NM0007
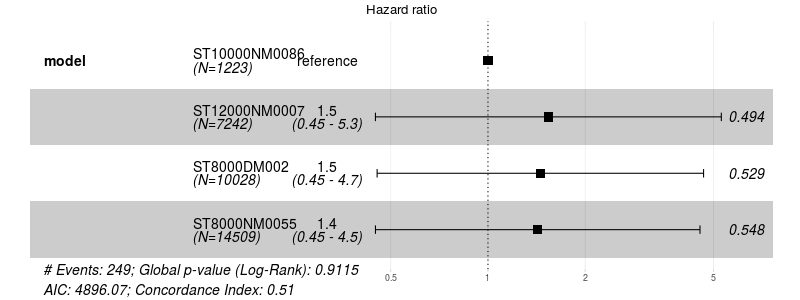
График 6: Модель кокса для больших накопителей, статистической разницы нет.
Если мы захотим сравнить десять самых популярных накопителей получается следующая картина:

График 7: Функции выживания для топ 10 накопителей
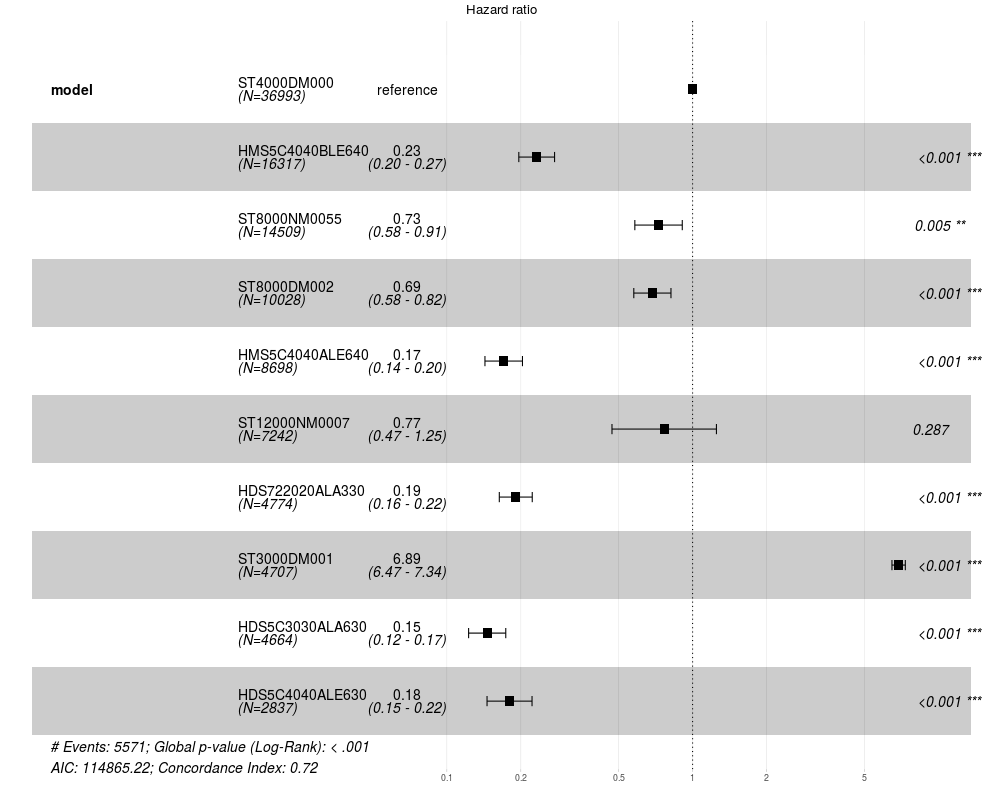
График 8: Модель кокса для 10 самых популярных накопителей
Самые надёжные: HDS5C3030ALA630, HMS5C4040ALE640, HDS5C4040ALE630, HDS722020ALA330, HMS5C4040BLE640, можно сделать попарное сравнение (функция pairwise_survdiff, если интересно есть-ли между ними разница.
Параметрические модели
Если нам интересно не просто сравнивать разные модели накопителей, а ответить на более конкретный вопрос типа: через какой промежуток времени скорее всего выйдет из строя один из двадцати дисков в моём файл сервере, то на помощь приходят параметрические модели.
Простейший случай — модель с постоянным риском, она предпологает что на всём протяжении жизни накопителя шанс умереть в данный промежуток времени — примерно одинаковый. Например, эта модель описывает процесс распада радиоизотопов. В литературе она называется экспоненциальной моделью, потому-что функции выживания описывается формулой
Когда вы рассчитываете % выхода из строя накопителей за год, то вы неявным способом используете эту модель.
На практике, известно что механические системы лучше описываются функцией Вейбулла, с формулой
если p<1, то вероятность отказов со временем уменьшается, p=1 — имеем экспоненциальную модель и p>1 — вероятность отказов со временем увеличивается.
В пакете survival для построения этой модели используется функция survreg:
Например, попробуем построить модель Вейбулла по 10 популярным накопителям:
fit_model_weibull<-survreg(Surv(age_days, status) ~ model, data=hdd_common)Сравним с экспоненциальной моделью
fit_model_exp<-survreg(Surv(age_days, status) ~ model, data=hdd_common,dist='exponential')И посмотрим как предсказанная функция распределения совпадает с непараметрической K-M, на примере ST4000DM000.
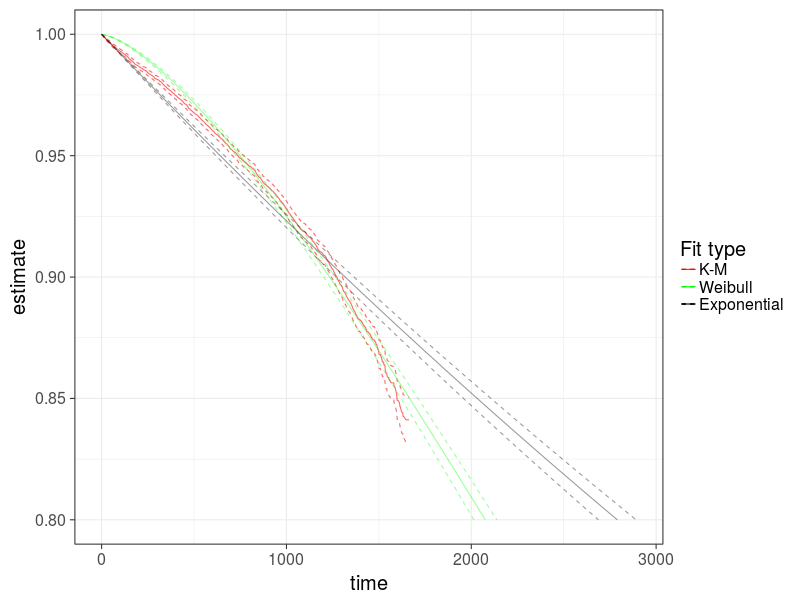
График 9: Сравнение двух параметрических моделей с непараметрической на примере ST4000DM000
Видно, что модель Вейбулла лучше описывает процесс выхода накопителей из строя.
Можно сравнить модели статистически, с помощью информационного критерия Акаике:
AIC(fit_model_weibull,fit_model_exp)
df AIC
fit_model_weibull 11 112208.8
fit_model_exp 10 112951.3Модель с меньшим значением AIC — лучше описывает наблюдаемые данные.
И посмотрим ожидаемое время выхода из строя 10% накопителей:
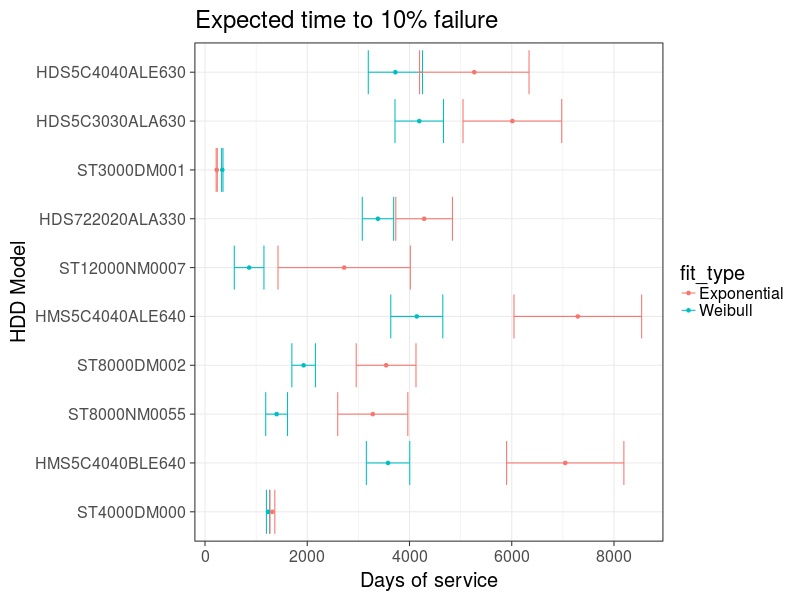
График 10: Оценка срока выхода из строя 10 самых популярных накопителей
На оценки видно, что модель Вейбула даёт более раннюю оценку выхода накопителей из строя. Кстати, если просто рассчитывать %% выхода накопителей из строя каждый год, то получается приближение экспоненциальной модели, которая в данном случаё даёт завышенный результат.
Заключение
Вот так, с помощью свободно выложенных данных по поломкам накопителей можно заниматься предсказанием будущих трат на замену дисков.
В массиве данных от backblaze есть ещё куча интересной информации, например можно посмотреть как температурный режим (параметр SMART 194) во время работы накопителя повлиял на срок его службы, или как количество циклов записи (параметр 241)
Скрипты и .csv файл для расчетов доступен на github.
Если есть интерес, можно куда-нибудь загрузить sqlite базу данных со всей базой данных backblaze (2.7ГБ после упаковки XZ)
Использованная литература
- Wikipedia: Survival analysis
- survminer: Survival Analysis and Visualization
- Michael J. Crawley. The R Book, 2nd edition ISBN: 978–0–470–97392–9
