Сравнение быстродействия def и lambda функций. Так все таки быстродействие или читабельность?
Идея для кода
Читая pep8, я наткнулся на пункт об использовании анонимных функций — по версии пепа, они снижают читабельность, если использовать переменную с значением функции как функцию, лучше использовать def. Я решил сравнить def и lambda по другому параметру — быстродействию. Я предполагал, что lambda, заточенный под однострочники , будет быстрее выполняться и создаваться. В этом исследовании я это проверю.
Библиотеки
Так как здесь будет много измерений времени, то несомненно, нам понадобится библиотека time, а также turtle, чтобы чертить разного рода графики. Я знаю, что это непрактично, но matprolib слишком долго (секунд 10) импортируется. Итак:
from turtle import *
from time import timeОбщие функции
В нашем коде для измерения быстродействия нужна… функция для измерения быстродействия. Она будет главной для всех производных. Прежде всего — мы не будем измерять время выполнения один раз, слишком велика погрешность. Функция будет принимать в аргументы функцию, для которой проводится замер, а также количество повторений этой функции.
Для самого измерения мы будем использовать разницу во времени между началом выполнения и концом. Из описания складывается код:
def speed_test(func, n):
start = time()
for i in range(n):
func()
stop = time()
return stop - startВсего у нас будет 2 диаграммы — полная и усредненная. В каждой по 2 графика — для def и lambda функций. Всего нам потребуется 4 черепахи.
Список значений для 1 и 2 графика очевиден — несколько результатов выполнения замера скорости. С 3 и 4 все сложнее — нужно найти среднее арифметическое одного из 2 первых графиков. Дабы слишком не заморачиваться над тем, чтобы график никуда не вылезал, найдем разницу между каждым элементом каждого графика и средним значением между средними арифметическими из 1 и 2 графика. В итоге, на графике мы будем видеть не общее значение, а разницу.
Все графики занесем в общий словарь, чтобы не создавать много переменных. Словарь заранее объявлен за пределами функции
def graph_data(func1, func2, mult1, mult2, arr_len):
l['l1'] = [func1(mult1)*mult2 for i in range(arr_len)]
l['l2'] = [func2(mult1)*mult2 for i in range(arr_len)]
l1_av = sum(l['l1']) // arr_len
l2_av = sum(l['l2']) // arr_len
av = sum((l1_av, l2_av)) / 2
l['l3'] = [l1_av - av for i in range(arr_len)]
l['l4'] = [l2_av - av for i in range(arr_len)]
for i in range(arr_len):
l['l1'][i] -= av
l['l2'][i] -= avФункции для упрощения жизни
Кому захочется повторять одно и то действие, но с разными параметрами? Никому. Поэтому, я и написал некоторые вспомогательные функции, для рисования графика по заданным параметрам, для создания черепахи. Кстати о последнем — черепаи тоже заносятся в общий словарь.
def draw(arr, t, x, mult=30):
n = len(arr)
t.up()
t.goto(-n*mult/2, 0)
for i, j in enumerate(arr):
t.goto(x+(-n*mult/2+i*mult), j)
t.down()
t.up()def add_turtle(name, color='#000000', width=2):
t[name] = Turtle()
t[name].pencolor(color)
t[name].width(width)
t[name].hideturtle()
t[name].speed('fastest')Производные функции
На этом этапе слабонервным людям, ненавидящим многоуровневые вложения, не читать.
Для ранее описанных общих функций можно создавать бесконечно много проиводных.
Для производной замера скорости структура такая:
def название(количество_повторений):
def функция_для_замера():
'''действия'''
return speed_test(функция_для_замера,
количество_повторений)А производная для функции построения графика — эта же самая функция с определенными аргументами.
Мы будем проверять скорость создания и скорость выполнения разного вида функций.
Вернемся к первому. В случае проверки скорости создания функции, функция_для_замера () будет иметь одну цель — создать внутри себя def или lambda функцию. Эту функцию мы будем вызывать множество раз, и каждый раз она будет создавать одну и ту же функцию заново. Иными словами — функцмя второго уровня вложенности служит для многократного вызова и создания во время каждого функции 3 уровня вложенности. Надеюсь, вы меня поняли.
Я мог бы сделать легче, но хотел сохранить структуру для всех производных функций.
Первые две производные — для создания пустых функций, возвращаюших False. Для def я мог бы написать с использованием return или pass, но в lambda это невозможно.
def test_empty_def(n):
def adding_def_func():
def test(): return False
return speed_test(adding_def_func, n)
def test_empty_lambda(n):
def adding_lambda_func():
test = lambda: False
return speed_test(adding_lambda_func, n)Следующие две — для таких же функций, но с простым выражением:
def test_def(n):
def adding_def_func():
def test(): return sum((2, 3, 4)) ** 0.5
return speed_test(adding_def_func, n)
def test_lambda(n):
def adding_lambda_func():
test = lambda: sum((2, 3, 4)) ** 0.5
return speed_test(adding_lambda_func, n)Еще две — для оценки скорости их создания + скорости выполнения:
def test_def2(n):
def adding_def_func():
def test(): return sum((2, 3, 4)) ** 0.5
test()
return speed_test(adding_def_func, n)
def test_lambda2(n):
def adding_lambda_func():
test = lambda: sum((2, 3, 4)) ** 0.5
test()
return speed_test(adding_lambda_func, n)Эти функции будут использованы в производных от graph_data:
def for_empty_func(arr_len):
graph_data(test_empty_def, test_empty_lambda, 10000, 20000, arr_len)
def for_one_eval_func(arr_len):
graph_data(test_def, test_lambda, 10000, 20000, arr_len)
def for_doing_func(arr_len):
graph_data(test_def2, test_lambda2, 10000, 20000, arr_len)Алгоритм
Дадим имя окну:
title('Сравнение def и lambda функций по скорости')Создадим 4 черепахи для рисования графика:
t = {}
add_turtle('t1', '#c80000')
add_turtle('t2', '#00c800')
add_turtle('t3', '#c80000')
add_turtle('t4', '#00c800')Опеределим длину диаграммы в вершинах:
arr_len = 20Подготовим данные для графиков и построим их:
l = {}
for i in range(5):
производная_от_graph_data(arr_len)
draw(l['l1'], t['t1'], -300)
draw(l['l2'], t['t2'], -300)
draw(l['l3'], t['t3'], 300)
draw(l['l4'], t['t4'], 300)Не забудем добавить событие закрытия окна:
exitonclick()Окончательный алгоритм
title('Сравнение def и lambda функций по скорости')
t = {}
add_turtle('t1', '#c80000')
add_turtle('t2', '#00c800')
add_turtle('t3', '#c80000')
add_turtle('t4', '#00c800')
arr_len = 20
l = {}
for i in range(5):
for_one_eval_func(arr_len)
draw(l['l1'], t['t1'], -300)
draw(l['l2'], t['t2'], -300)
draw(l['l3'], t['t3'], 300)
draw(l['l4'], t['t4'], 300)
exitonclick()
Полный код
from turtle import *
from time import time
def speed_test(func, n):
start = time()
for i in range(n):
func()
stop = time()
return stop - start
def test_empty_def(n):
def adding_def_func():
def test(): return False
return speed_test(adding_def_func, n)
def test_empty_lambda(n):
def adding_lambda_func():
test = lambda: False
return speed_test(adding_lambda_func, n)
def test_def(n):
def adding_def_func():
def test(): return sum((2, 3, 4)) ** 0.5
return speed_test(adding_def_func, n)
def test_lambda(n):
def adding_lambda_func():
test = lambda: sum((2, 3, 4)) ** 0.5
return speed_test(adding_lambda_func, n)
def test_def2(n):
def adding_def_func():
def test(): return sum((2, 3, 4)) ** 0.5
test()
return speed_test(adding_def_func, n)
def test_lambda2(n):
def adding_lambda_func():
test = lambda: sum((2, 3, 4)) ** 0.5
test()
return speed_test(adding_lambda_func, n)
def add_turtle(name, color='#000000', width=2):
t[name] = Turtle()
t[name].pencolor(color)
t[name].width(width)
t[name].hideturtle()
t[name].speed('fastest')
def draw(arr, t, x, mult=30):
n = len(arr)
t.up()
t.goto(-n*mult/2, 0)
for i, j in enumerate(arr):
t.goto(x+(-n*mult/2+i*mult), j)
t.down()
t.up()
def graph_data(func1, func2, mult1, mult2, arr_len):
l['l1'] = [func1(mult1)*mult2 for i in range(arr_len)]
l['l2'] = [func2(mult1)*mult2 for i in range(arr_len)]
l1_av = sum(l['l1']) // arr_len
l2_av = sum(l['l2']) // arr_len
av = sum((l1_av, l2_av)) / 2
l['l3'] = [l1_av - av for i in range(arr_len)]
l['l4'] = [l2_av - av for i in range(arr_len)]
for i in range(arr_len):
l['l1'][i] -= av
l['l2'][i] -= av
def for_empty_func(arr_len):
graph_data(test_empty_def, test_empty_lambda, 10000, 20000, arr_len)
def for_one_eval_func(arr_len):
graph_data(test_def, test_lambda, 10000, 20000, arr_len)
def for_doing_func(arr_len):
graph_data(test_def2, test_lambda2, 10000, 20000, arr_len)
title('Сравнение def и lambda функций по скорости')
t = {}
add_turtle('t1', '#c80000')
add_turtle('t2', '#00c800')
add_turtle('t3', '#c80000')
add_turtle('t4', '#00c800')
arr_len = 20
l = {}
for i in range(5):
for_one_eval_func(arr_len)
draw(l['l1'], t['t1'], -300)
draw(l['l2'], t['t2'], -300)
draw(l['l3'], t['t3'], 300)
draw(l['l4'], t['t4'], 300)
exitonclick()
Тесты
Переходим к главному — что же быстрее? Зеленым на графике обозначены lambda, красным — def
Первый тест — на скорость создания пустой (почти) функции:
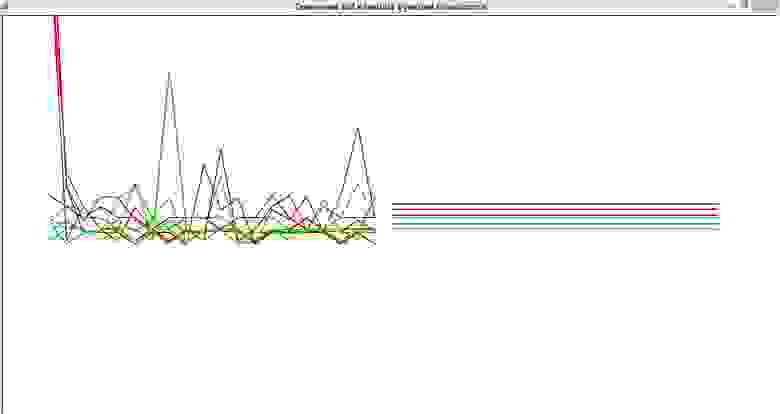 скорость создания пустой (почти) функции
скорость создания пустой (почти) функции
Второй тест — на скорость создания скорости с выражением:
 скорость создания скорости с выражением
скорость создания скорости с выражением
Третий тест — на скорость создания и выполнения:
 на скорость создания и выполнения
на скорость создания и выполнения
Во всех случаях ведут lambda функции.
Выводы
Для повышения читабельности в любом случае используйте def, ну, а если скорость в приоритете — не используйте питон, лол. Ну, а если серьезно, то статья кому-то может оказаться полезной, ведь Python идеально подходит для некоторых задач, так почему-бы эти задачи не оптимизировать?
