Соблюдаем дистанцию, как топологи
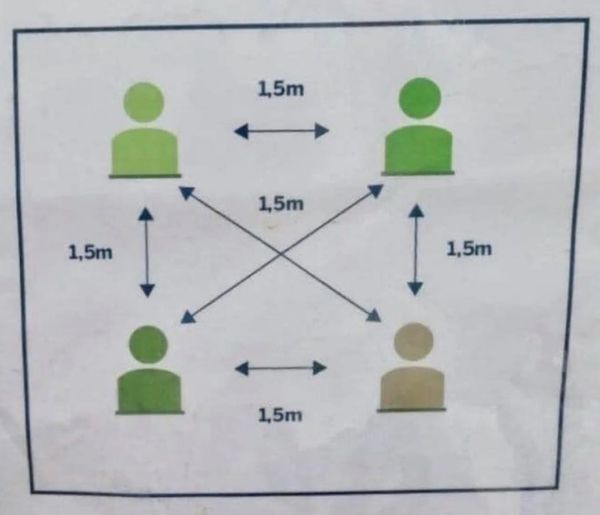
За минувшие пандемийные годы кто только не прошёлся по этой картинке, обсуждая невозможность выполнения такого требования на плоскости! Теперь, когда страсти поутихли, мне бы хотелось обсудить естественное математическое развитие этой темы в форме вопроса:
А где и как это возможно? Каким образом в различных топологиях можно расположить максимальное количество точек, так чтобы расстояния между любыми двумя точками было бы одинаковым?
Метрики бывают разными, здесь, для определённости, мы сосредоточимся на евклидовой метрике, а менять будем топологию пространств.
Евклидовы пространства
На плоскости мы без труда разместим три попарно равноудалённые точки по вершинам равностороннего треугольника. Если попробуем поместить четвёртую, то она сможет оказаться лишь в одной из трёх позиций, равноудалённой от двух из трёх уже поставленных точек, однако третья точка при этом оказывается слишком далеко.
Нам как-то нужно отождествить эти три позиции, собрав их «в кучку». На плоскости мы это сделать не сможем, но если сумеем как-то подняться над ней в третьем измерении, то нам удастся собрать все три позиции в одну и получить вершины правильной треугольной пирамиды — тетраэдра.
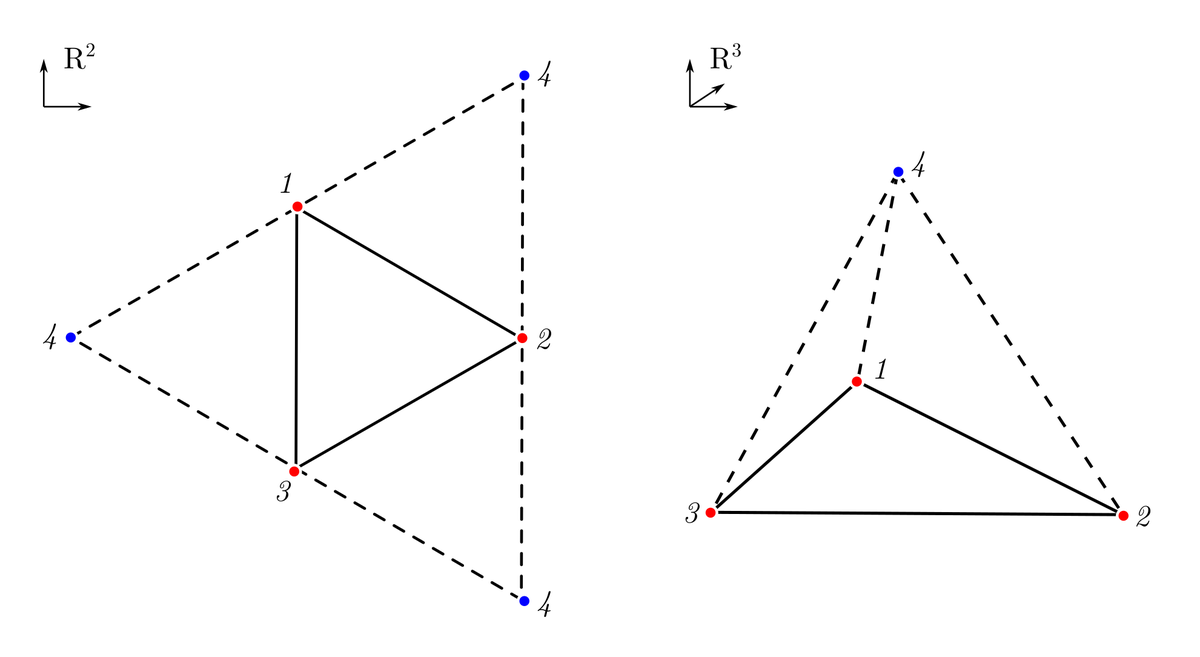
Построение тетраэдра, как результата отождествления трёх точек в одну.
Добавление пятой точки приведёт нас к таким же рассуждениям и к необходимости как-то собрать в одну точку четыре позиции, равноудалённых от трех граней тетраэдра. Для их отождествления нам потребуется уже четвёртое измерение. Поднявшись в нëм, мы сможем их соединить и получить вершины пятиячейника — четырёхмерного аналога тетраэдра. Так можно продолжать сколько угодно, уходя во всё более высокие размерности.
Метод добавления точек по одной подсказывает нам, что иных множеств с заданным свойством в евклидовых мирах получить не получится. При использовании евклидовой метрики в пространстве размерности максимальноеколичество равноудалённых точек равно
. Эти точки будут расположены в вершинах симплексов — простейших правильных многогранниках в евклидовых пространствах. На картинке, вынесенной в заголовок, соответственно, показан трёхмерный случай.
Все эти множества условно можно изобразить в форме графов, в котором рёбра соответствуют одному и тому же расстоянию между точками.
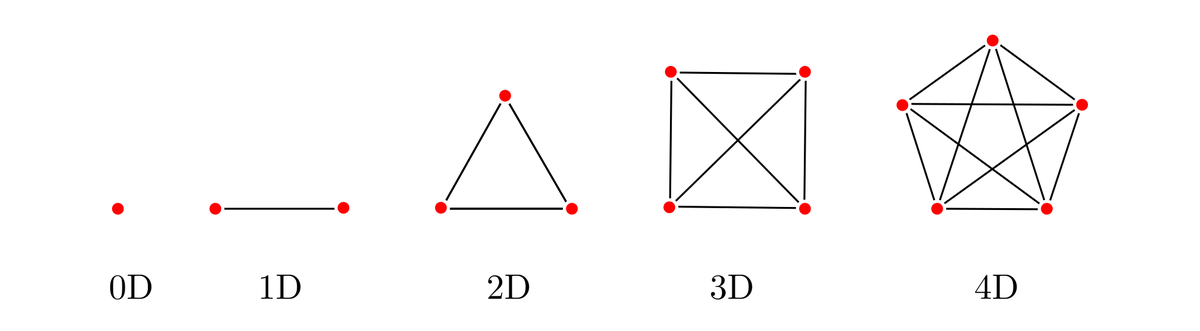
Симплексы — простейшие правильные многогранники в евклидовых пространствах разных размерностей, показанные в форме графов.
Все графы, представляющие симплексы, полные. Это значит, что каждая вершина в них связана рёбрами со всеми другими. Полнота графа является одним из условий нашей задачи, однако добавленное нами требование равенства всех расстояний между узлами делает эти графы особенными. Будем называть их полными равносторонними графами и обозначать где
обозначает число вершин.
Одномерные многообразия
Топологически евклидовы пространства устроены достаточно просто, а что если перейти к иным топологиям? Я ограничусь здесь рассмотрением одномерных и двумерных связных многообразий: таких пространств, которые в каждой точке локально неотличимы от евклидового пространства такой же размерности.
Для одномерных многообразий есть лишь два принципиально различных варианта топологии: вещественная прямая (интервал) и окружность (петля). На прямой, как мы видели, равноудалены могут быть только две точки, тогда как на петле уже есть возможность расположить третью точку.
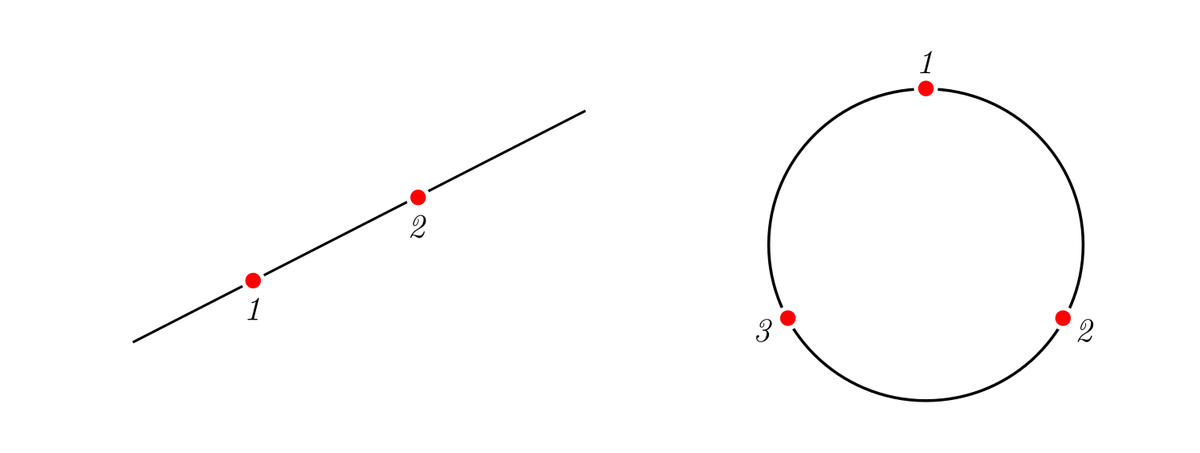
Рпвноудалëнные точки на одномерных многообразиях.
Если представить, что окружность выполнена из нерастяжимой нити, то её форма не будет иметь значения, при любом искажении линии, расстояния между точками не изменятся.
Можно было бы поступить прямолинейно и из нерастяжимых ниток одинаковой длины изготовить полный граф с произвольным числом вершин. Точки, принадлежащие нитям образуют одномерное пространство, но оно не является многообразием, поскольку в произвольной окрестности любого из узлов графа (то есть, интересующих нас точек), пространство не будет иметь эвклидовой топологии. Такое решение, состоящее исключительно из особых точек, не особо интересно.
Двумерные многообразия
Во всех дальнейших рассуждениях под расстоянием между точками мы будем понимать расстояние, измеряемое с помощью евклидовой метрики, но так, чтобы все кратчайшие пути принадлежали исследуемой поверхности. Можно представить себе, что расстояния, измеряются муравьём, который ползает по поверхности с обыкновенным евклидовым курвиметром, не имеет никакой возможности покинуть эту поверхность, подпрыгнув или взлетев, но способен найти кратчайший путь между двумя точками.
Отличия от топологии евклидовой плоскости подразумевают то или иное искривление пространства. И тут нас, как котёнка по имени Гав во дворе, поджидают неприятности. Искривлённые метрические пространства бывают коварными и без понимания дифференциальной геометрии и аккуратного использования метрического тензора, лучше туда не лезть, чтобы ничего не напутать. Но задачка-то у нас носит скорее развлекательный характер, хотелось бы обойтись без тензоров, геодезических линий и вариационного исчисления.
Поскольку нас будет интересовать только топология поверхностей, которая, не зависит от такой характеристики, как кривизна, а именно она создаëт сложности в измерениях расстояний, мы можем договориться рассматривать либо развёртываемые поверхности, либо, если это невозможно — плоские топологические модели поверхностей.
Развёртываемой называют поверхность, которую можно изометрично (без искажений размеров и площадей) и взаимооднозначно отобразить на плоскость. Такую поверхность можно обернуть листом бумаги без разрывов и растяжений, либо развернуть в плоский лист, получив её развёртку, своеобразную «карту». На развёртке кратчайшим путём между любыми двумя точками, будет прямолинейный отрезок. При сворачивании такой карты обратно в поверхность иной топологии, отображение этого отрезка на поверхности тоже будет кратчайшим путём между отображениями этих двух точек.
Цилиндрические и конические поверхности
Взяв лист бумаги и изогнув его так, как показано на рисунке, мы получим фрагмент цилиндрической поверхности. Так как плоская развёртка и цилиндрическая поверхность изометричны, нам абсолютно неважно какой именно формы будет огибающая кривая. Важно только замкнута она или нет.
Вложение графа E₃ на поверхность, эквивалентную плоскости
Если кривая огибающая цилиндр незамкнута, то поверхность ничем не отличается от плоскости или от диска, и на ней можно найти только три равноудалённые точки.
В случае замкнутой огибающей, на карте такой поверхности две стороны карты отождествляются (склеиваются). При этом можно расположить четыре равноудалённые друг от друга точки так, как показано на рисунке:
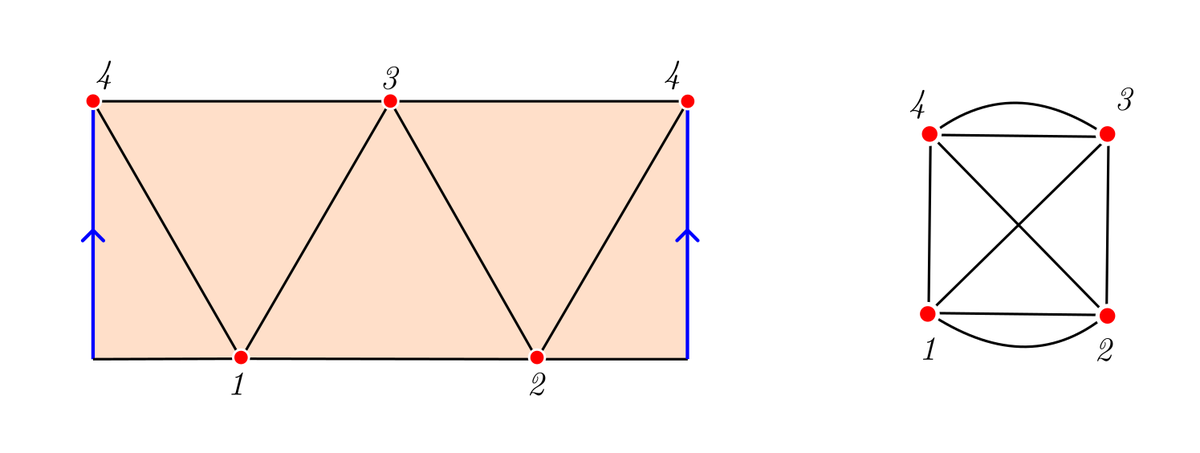
Эти точки образуют полный граф с четырьмя узлами и двумя дублирующимися ребрами.
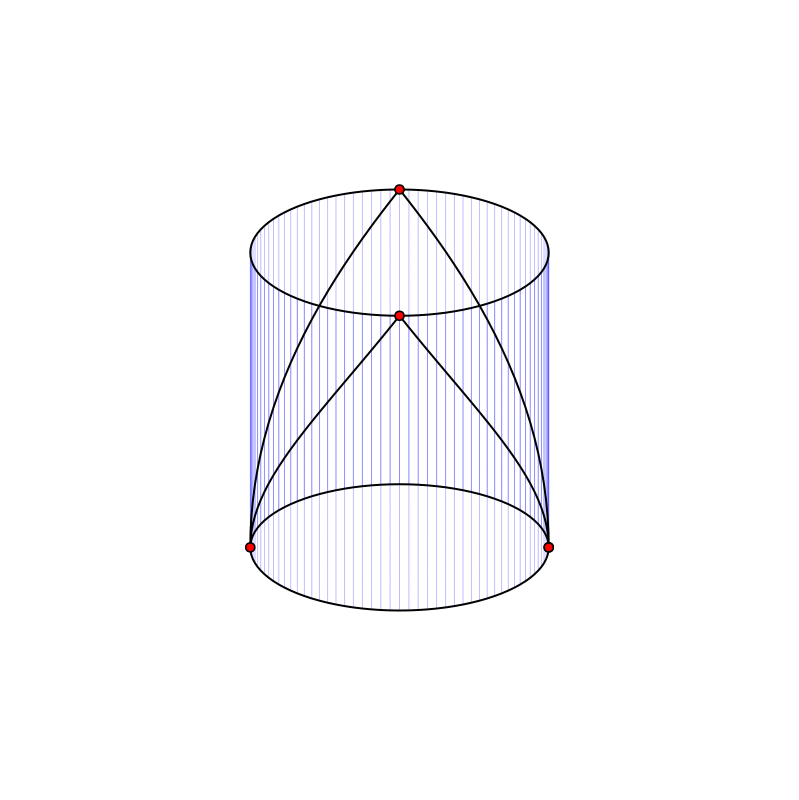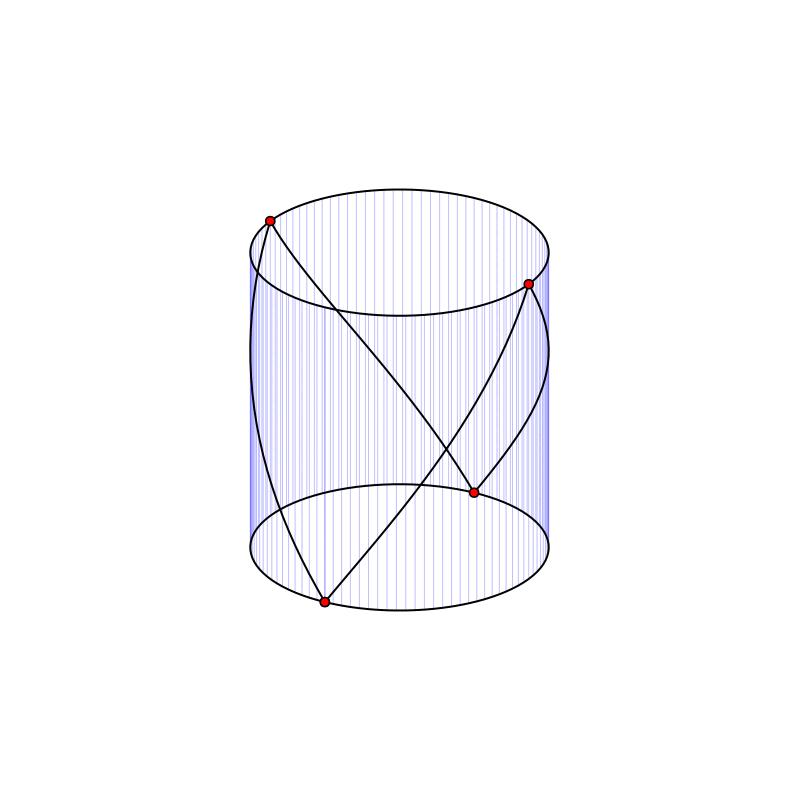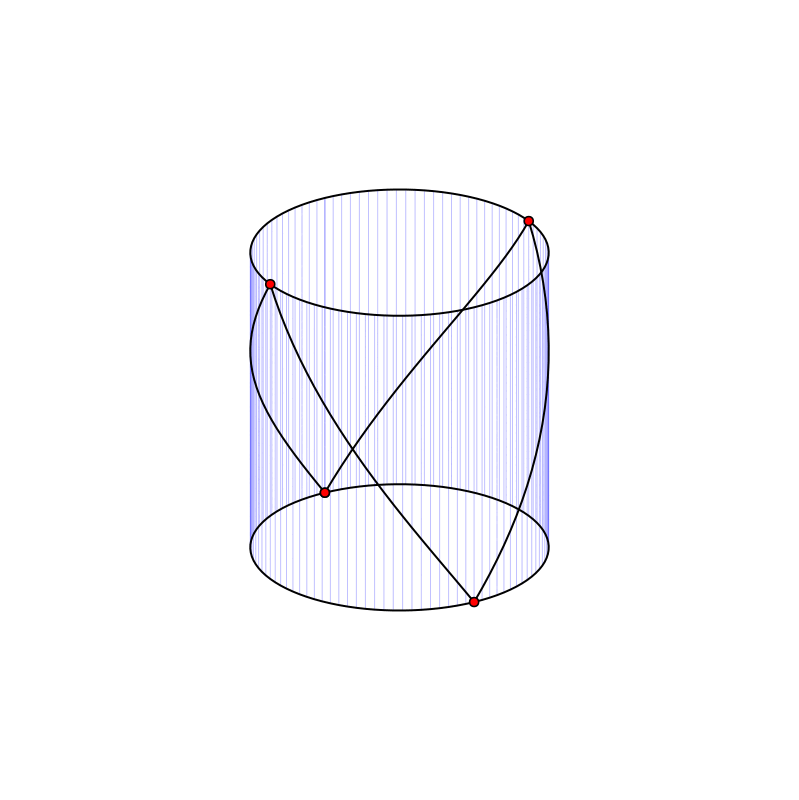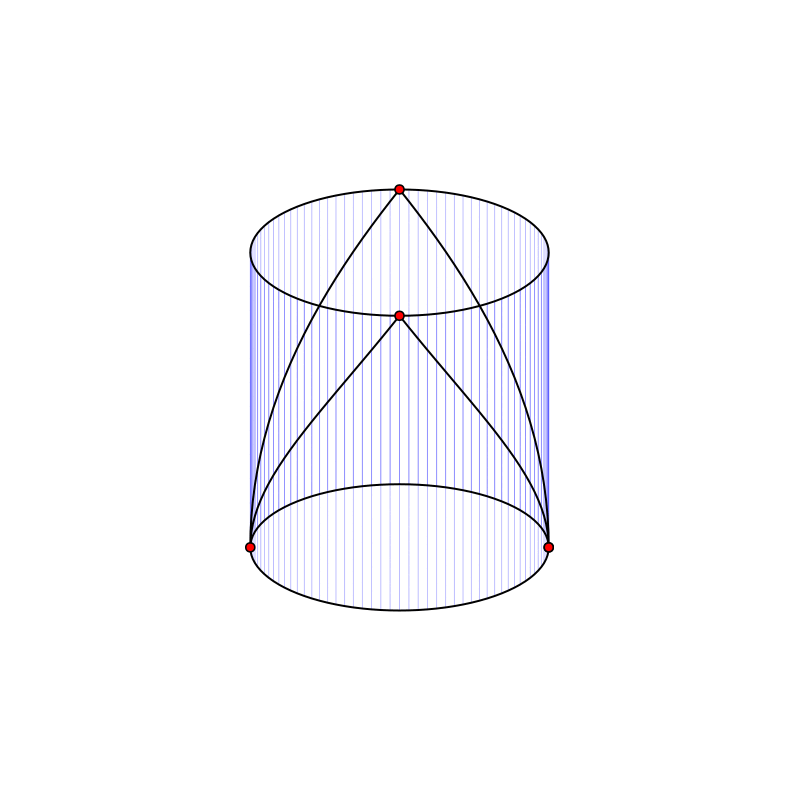
Вложение графа E₄ на цилиндрической поверхности.
Если мы свернём бумажный лист в кулёк, то получим коническую поверхность. Её можно получить вращением в пространстве прямой, вокруг оси, пересекающей прямую под каким-то углом. Почти на всех конусах можно разместить не более трёх равноудалённых точек, как на петле. Но есть особый случай для конуса с углом между осью вращения и образующей конус прямой равным 30°:
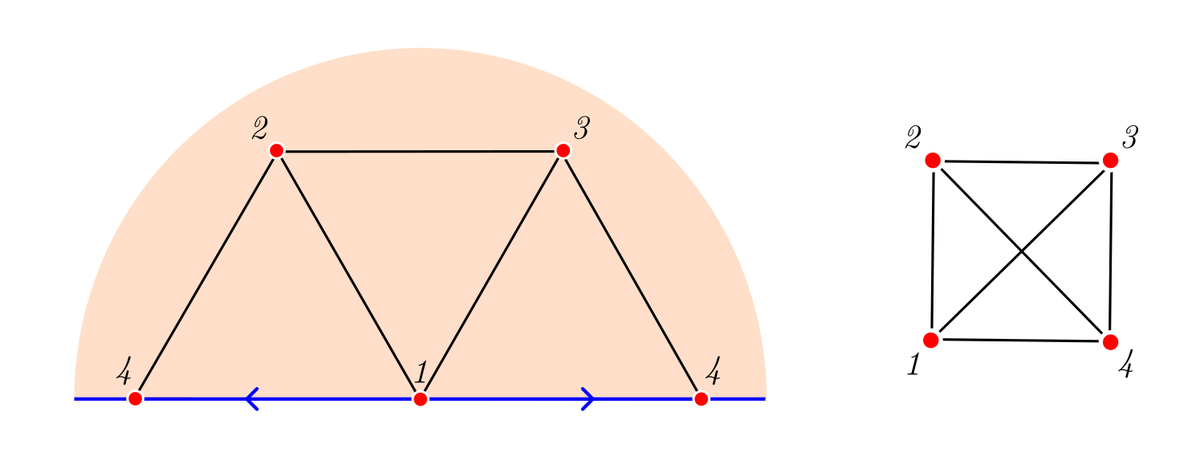
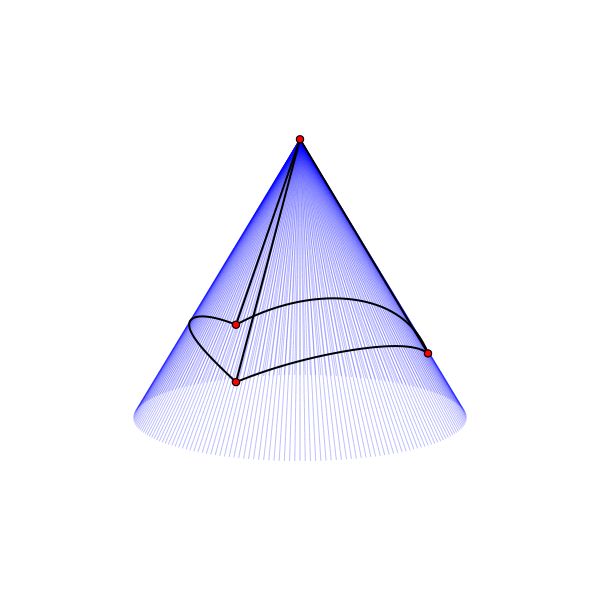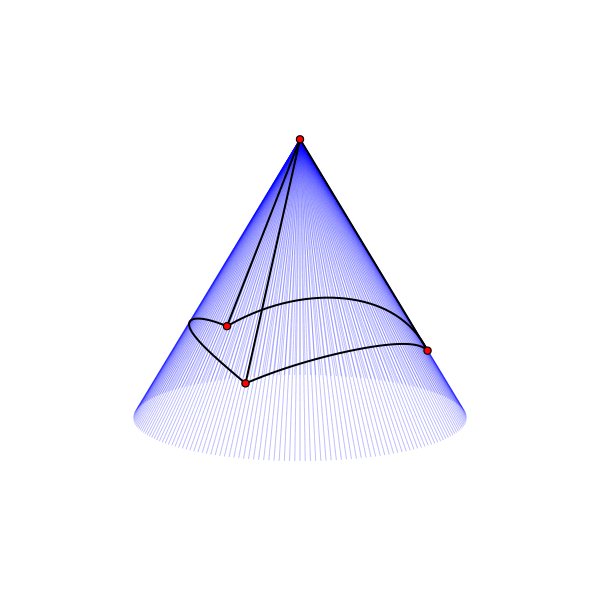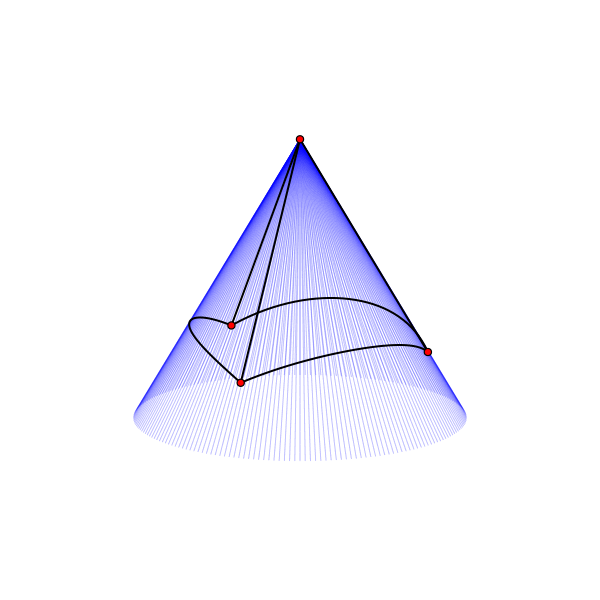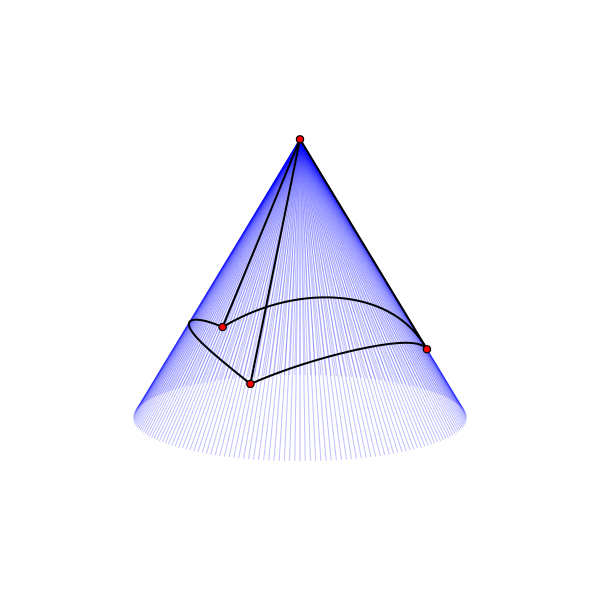
Четыре эквидистантные точки на конической поверхности.
Тут можно заметить, что однополостный конус топологически эквивалентен открытому диску или евклидовой плоскости. Почти на всех конусах единственным решением будет граф Но наша задача не чисто топологическая, в ней существенную роль играет метрика, так что искривление конической поверхности позволяет нам получить решение в форме графа
Сфера
Сфера не является развёртываемой поверхностью, но на ней определяется очень хорошая метрика со всюду одинаковым метрическим тензором. На сфере, как и на цилиндре, размещается максимум четыре равноудалённые точки.
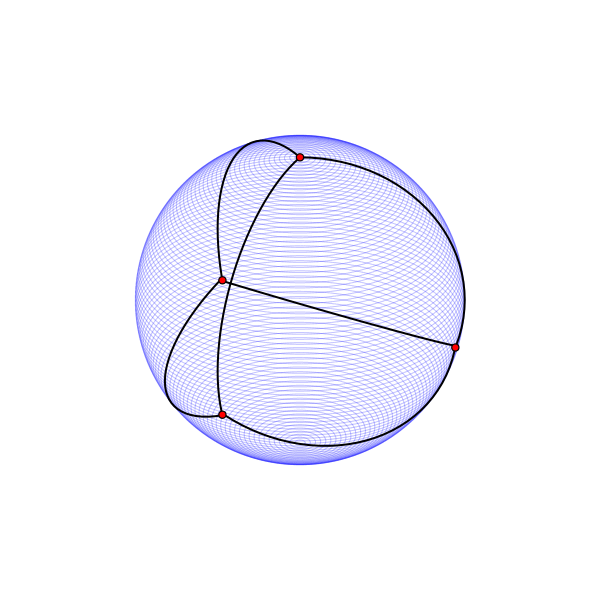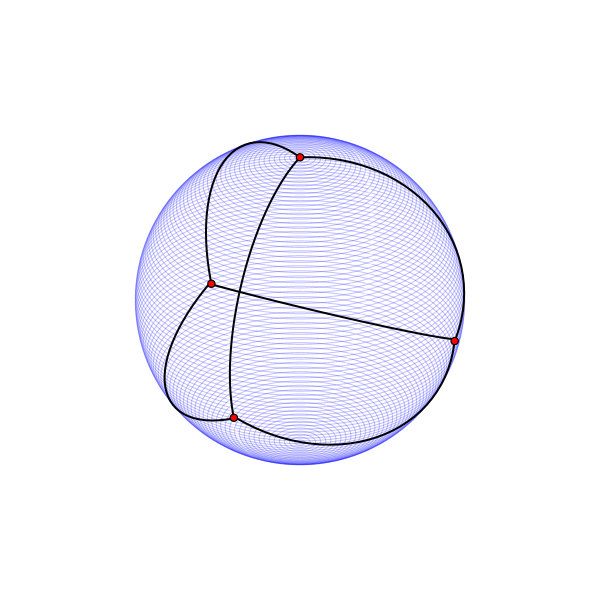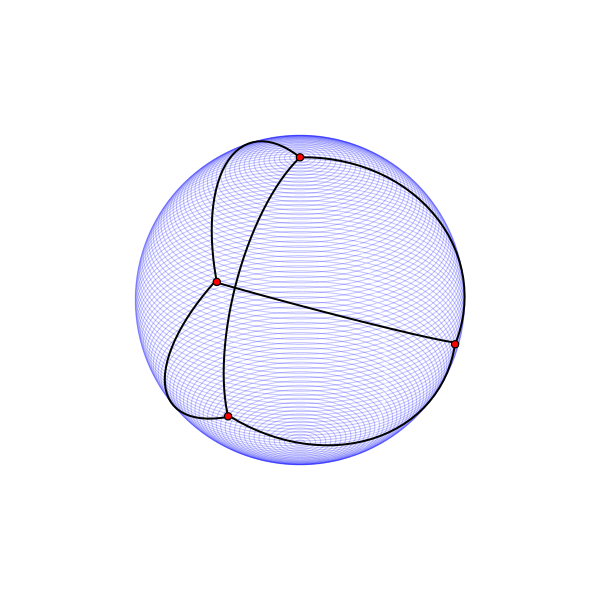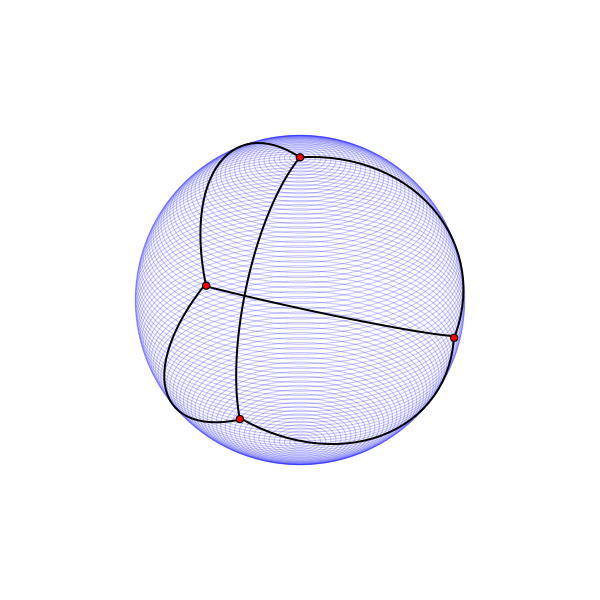
Вместо искривлённой сферы можно рассмотреть кусочно-плоские выпуклые многогранники, которые имеют плоские развёртки. На поверхности любого из них можно разместить вершины графа .
Лента Мёбиуса
Прямоугольную развёртку можно склеить не только в цилиндрическую поверхность, но и в ленту Мёбиуса. И тут у нас появляется возможность разместить пятую точку, равноудалённую от четырёх равноудалённых, не переходя в четвёртое измерение:
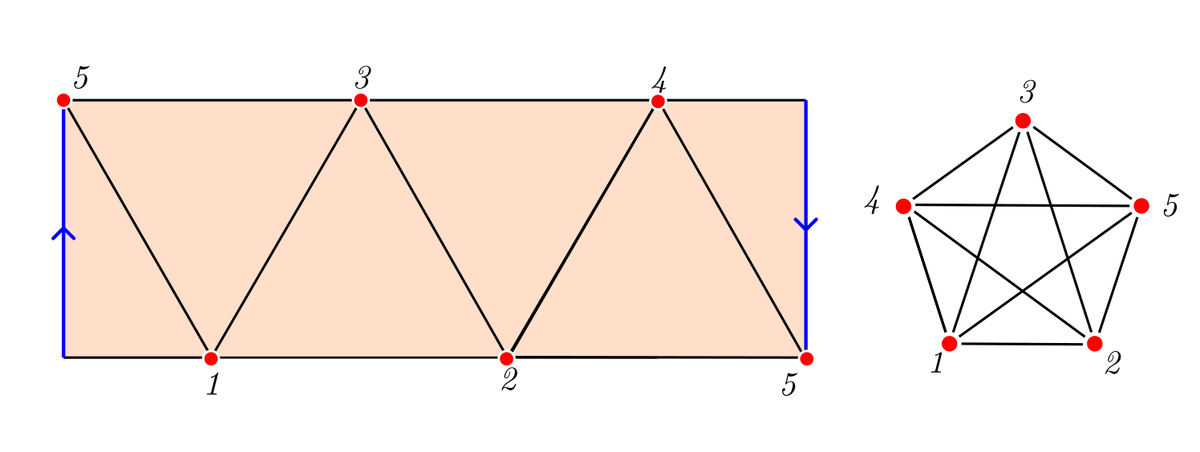
Вложение графа E₅ на ленту Мёбиуса.
Если мы вложим эту ленту в трёхмерное пространство, воспользовавшись канонической параметризацией ленты Мёбиуса, получится красивая картинка, отражающая топологию, но при этом изменяющая расстояния между точками.

Вложение ленты Мёбиуса, не изометричное плоской развёртке.
Для ленты Мёбиуса существует плоское вложение в трёхмерное пространство, изометричное плоскости, и которое легко изготовить из бумаги:

Тор
Если склеить две противоположные стороны прямоугольной развёртки, то получится топология тора. Однако это не даёт никаких преимуществ в отношении размещения равноудалённых точек по сравнению с цилиндром: их будет только четыре. Изменится лишь граф: он не просто остаётся полным, все его рёбра дублируются.
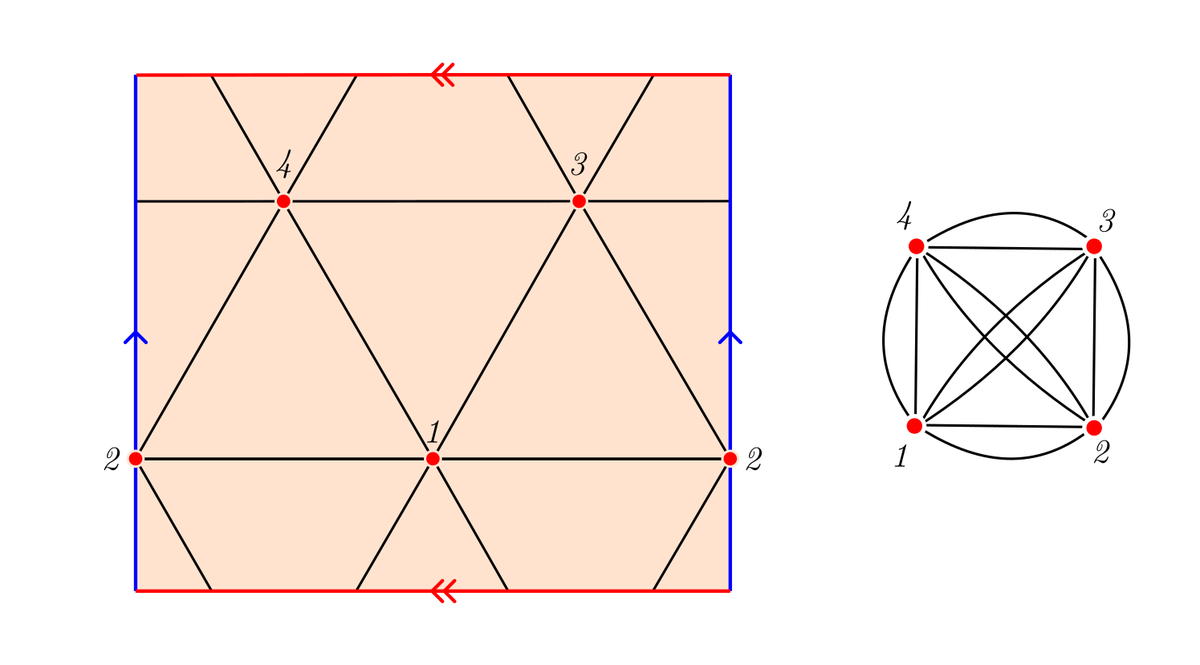
Оставить плоский тор плоским после склеивания возможно, но не так уж и просто. Для этой заметки я покажу модель, показывающую как именно располагаются точки и отрезки, но искажающую расстояния.
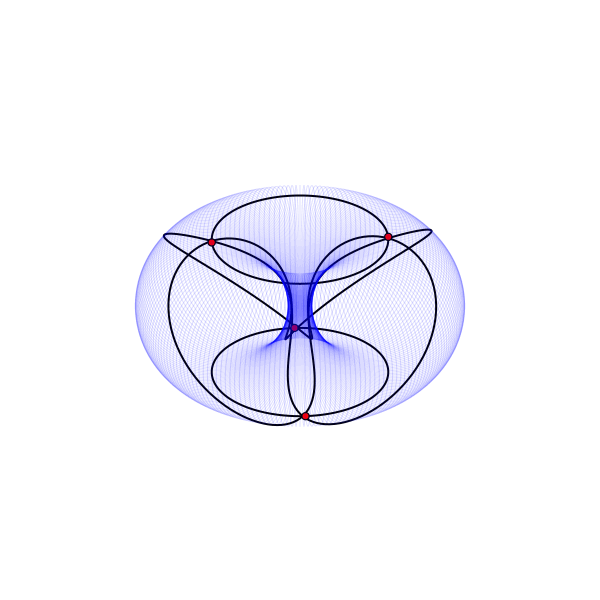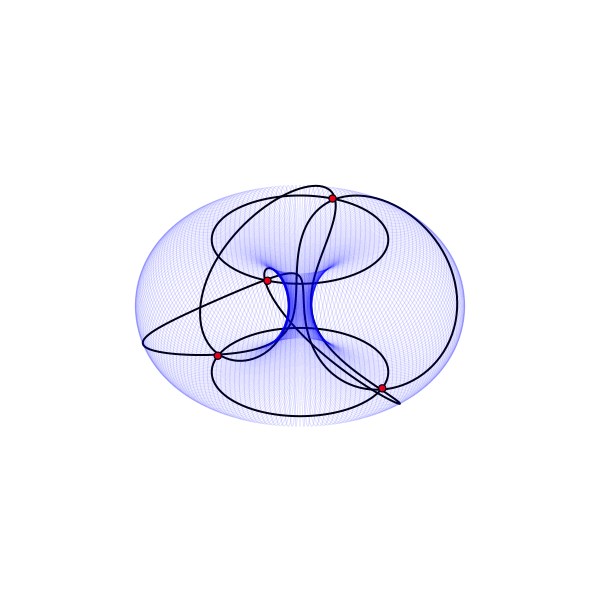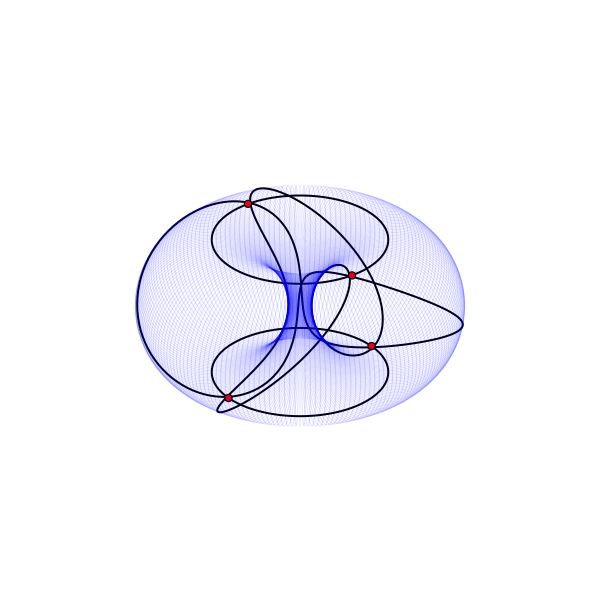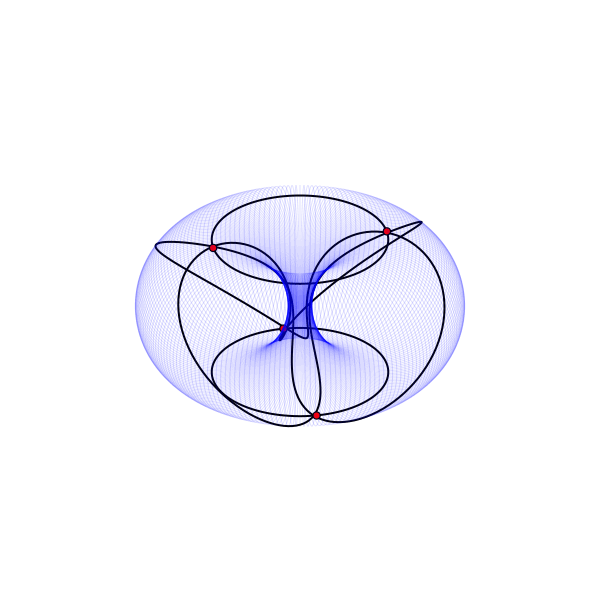
Портрет вложения графа E₄ на поверхность тора.
При попытке расположить точки на привычном круглом торе мы ожидаемо столкнёмся с метрическими и геодезическими трудностями. Достаточно показать какими могут быть геодезические линии на торе, вдоль которых надо вычислять расстояния между точками.
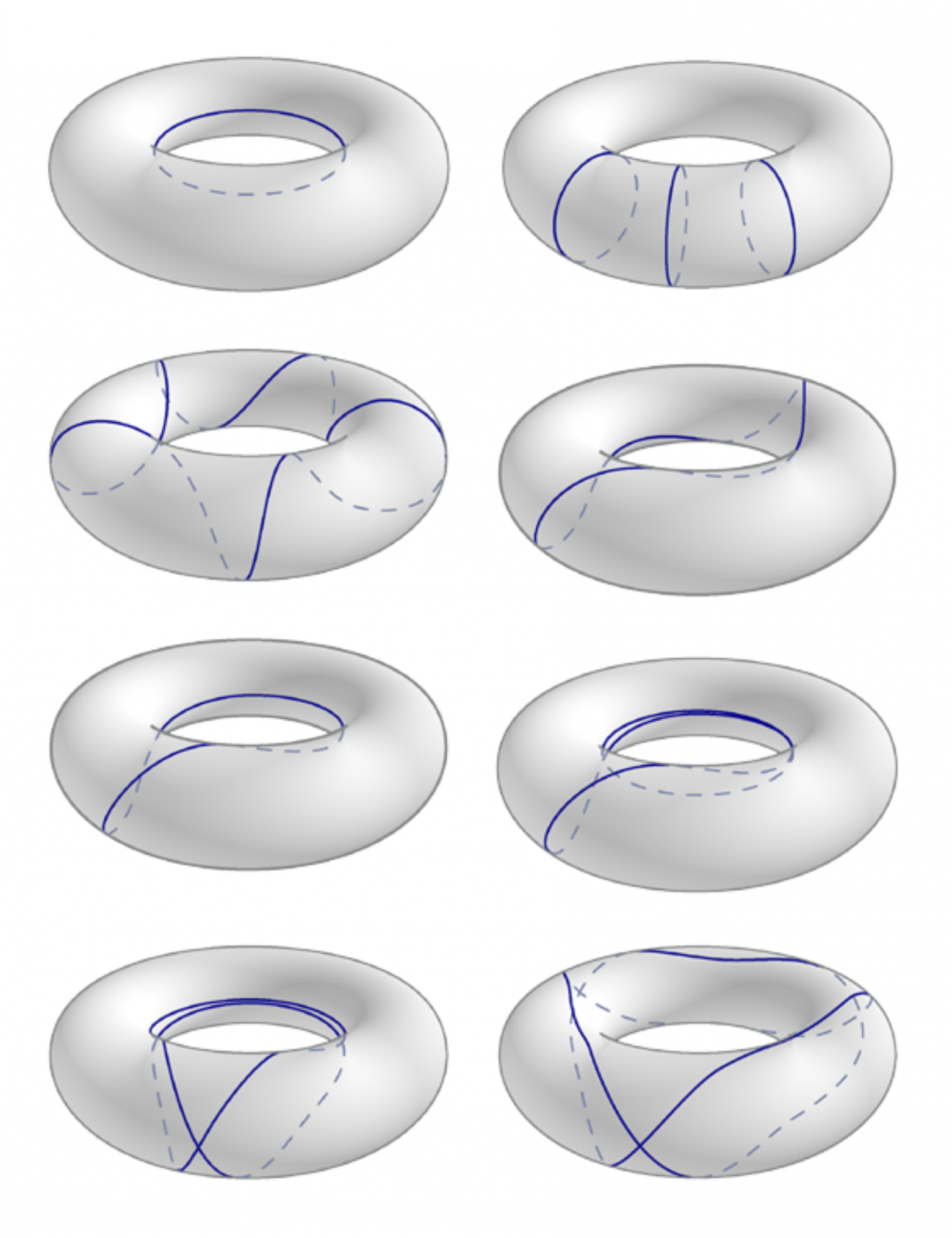
Иллюстраци Марка Айрона.
Вместо гладкого можно выбрать какое-либо кусочно-плоское вложение плоского тора в , например, в виде тороидального многогранника, например, многогранника Часара. Наконец, можно заморочиться и использовать
— гладкое изометричное вложение тора, обладающее фрактальной структурой.

Бутылка Клейна
Так же как и в случае ленты Мёбиуса, скручивание развёртки тора позволяет добавить пятую точку. При этом получается односторонняя компактная поверхность без края, которая называется бутылкой Клейна.
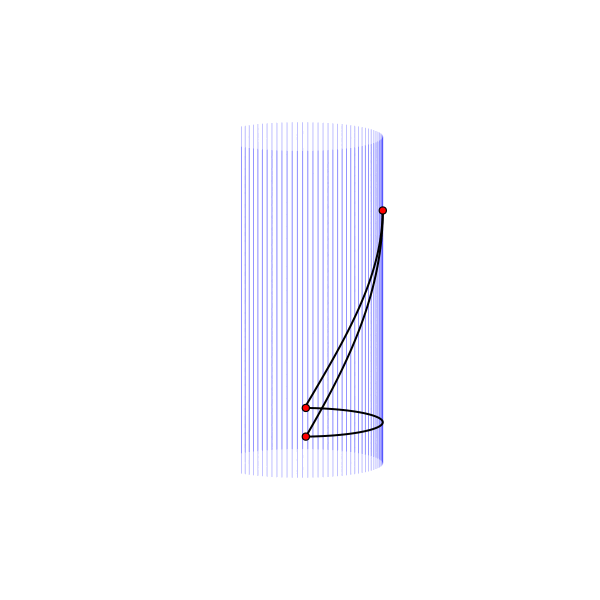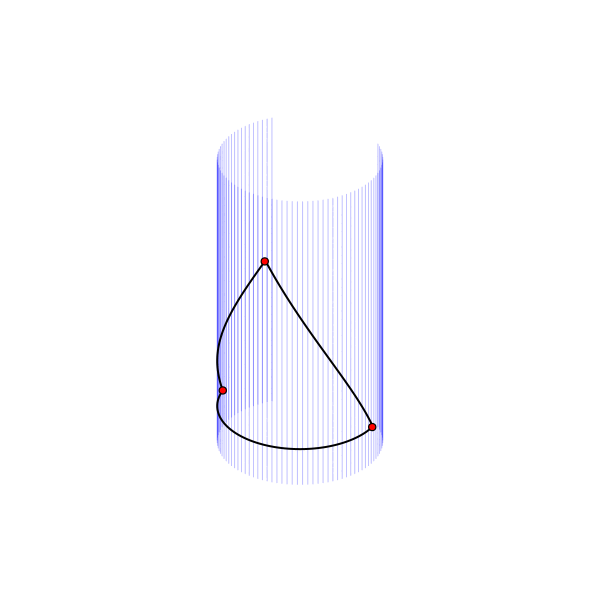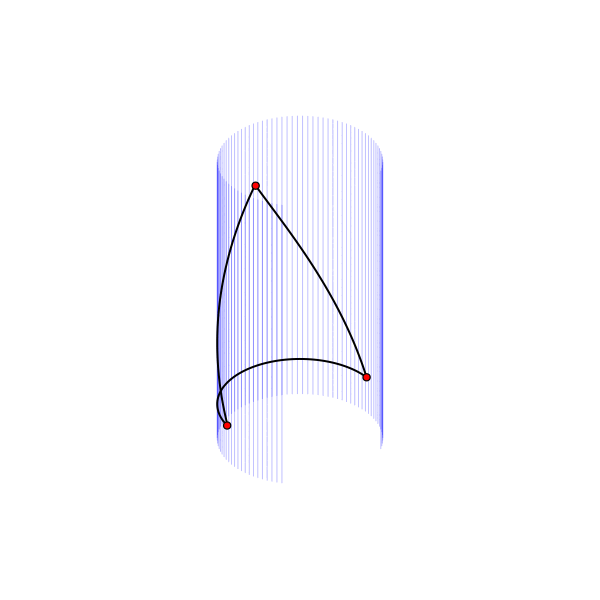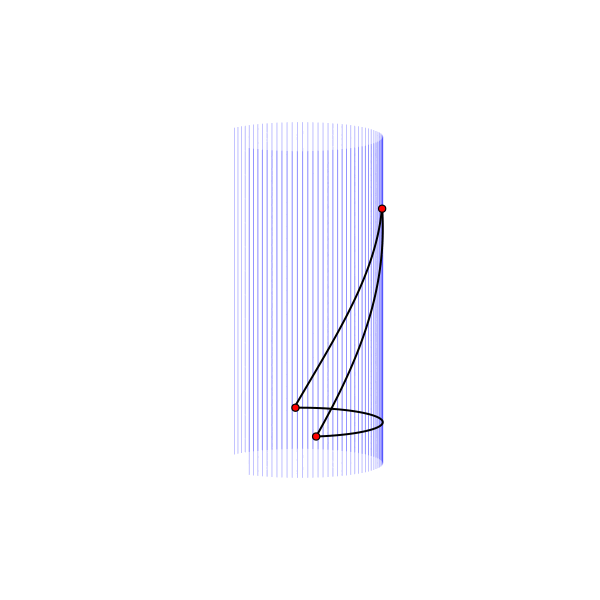
Бутылка Клейна тоже не является развёртываемой поверхностью. Приведу здесь, в качестве иллюстрации, красивую параметризацию этой поверхности, описывающее её погружение в трёхмерное пространство. Чтобы не перегружать и без того непростую картинку, покажу здесь только одну линию, соединяющую пять равноудалённых точек. При этом между любыми двумя точками существует кратчайший путь (не показанный здесь), который для всех точек имеет одинаковую длину.

Вещественная проективная плоскость
Есть ещё одна поверхность, которую можно получить, склеивая стороны прямоугольной развёртки: вещественная проективная плоскость. Она получается отождествлением точек, симметричных относительно центра развёртки. Представить её себе непросто, к тому же, подобно бутылке Клейна, она не может быть вложена в трёхмерное пространство без самопересечений.
Проективная плоскость получается склейкой единственного края ленты Мёбиуса с краем диска. По краю ленты Мёбиуса мы смогли расположить пять равноудалённых точек, на диске теоретически можно было бы поместить ещё одну, шестую точку, так чтобы она оказалась на одинаком расстоянии от этих пяти.
Кроме склеивания противоположных точек на краю диска, или заклеивания ленты Мёбиуса, проективную плоскость можно получить из сферы, отождествив все антиподальные точки, то есть, точки, симметричные относительно центра сферы. Это, с одной стороны, позволяет нам задать на проективной плоскости метрику, подобную сферической, а с другой, позволяет строить замощения проективной плоскости правильными многоугольниками. Так определяются абстрактные многогранники: полукуб, полуоктаэдр, полудодекаэдр и полуикосаэдр. Их невозможно склеить из бумаги или нарисовать в объёме, но они могут быть изображены в виде графа, а метрика позволяет говорить о том, что длины ребер этих многогранников одинаковы.
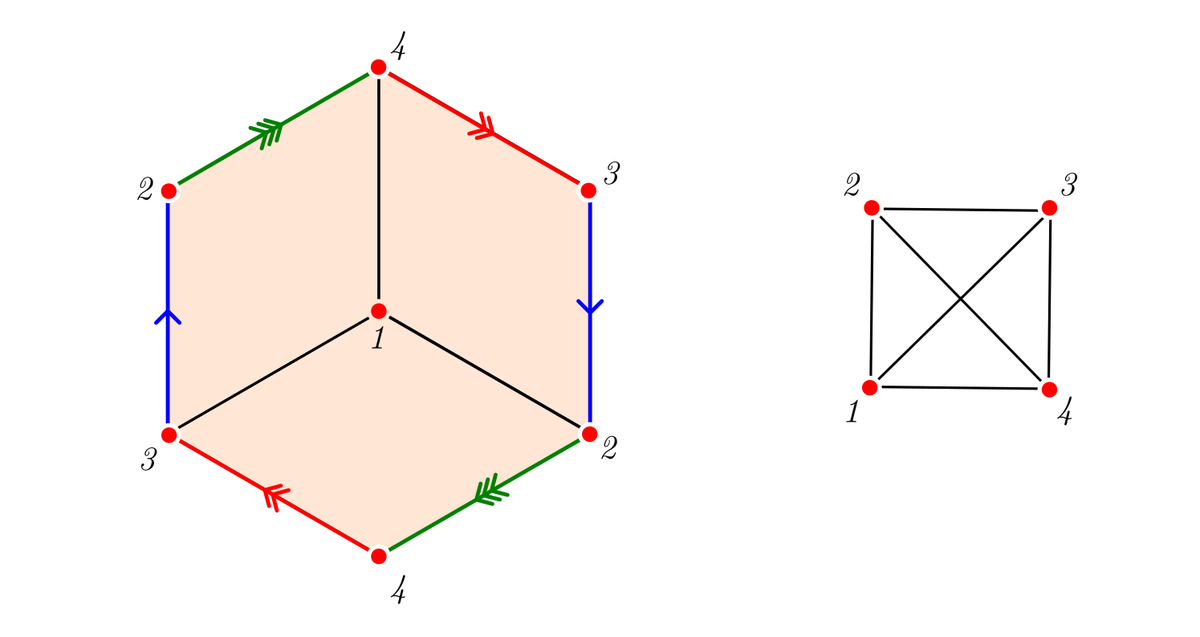
Полукуб — самое странное вложение графа на двумерное многообразие.
Полукуб интересен тем, что образует множество равноудалённых точек, но расположенных не в вершинах треугольников, а в вершинах квадратов. Поищите их образы в графе Благодаря топологии проективной плоскости, кратчайшее расстояние между вершинами, расположенными по диагонали, равно стороне квадрата.
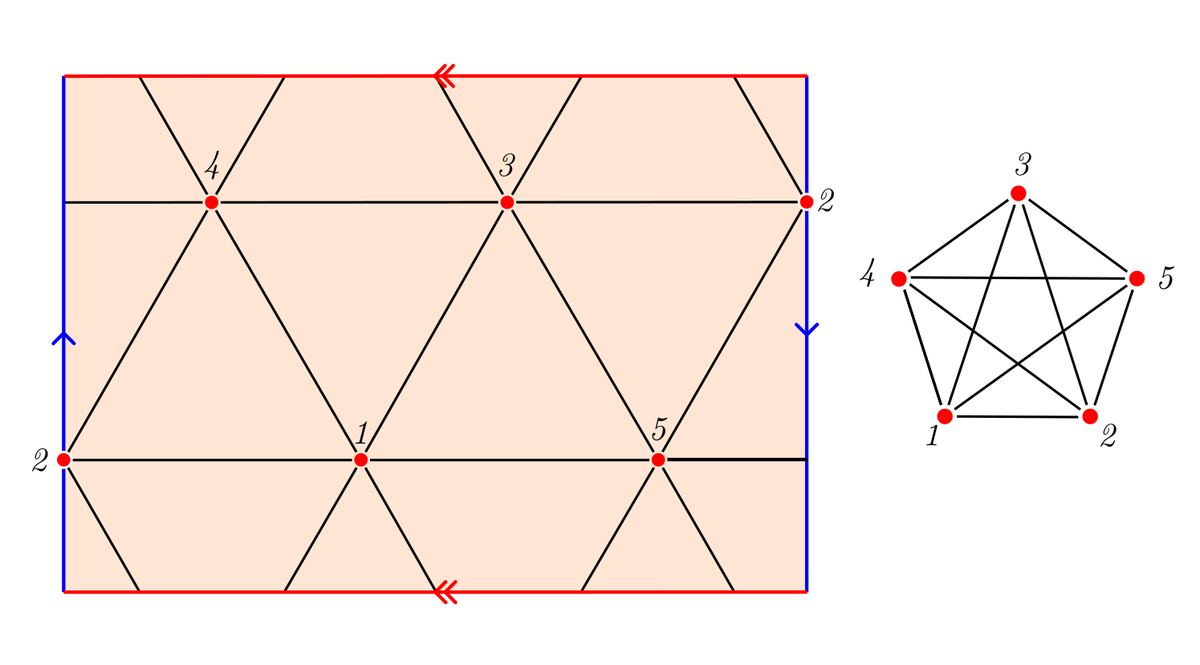
Полуоктаэдр не очень интересен, а вот полуикосоэдр дарит нам рекорд среди множеств равноудалённых точек на компактных двумерных многообразиях: предсказанные шесть точек. Если аккуратно перенести все ребра полуикосаэдра на граф, то станет очевидно, что перед нами граф
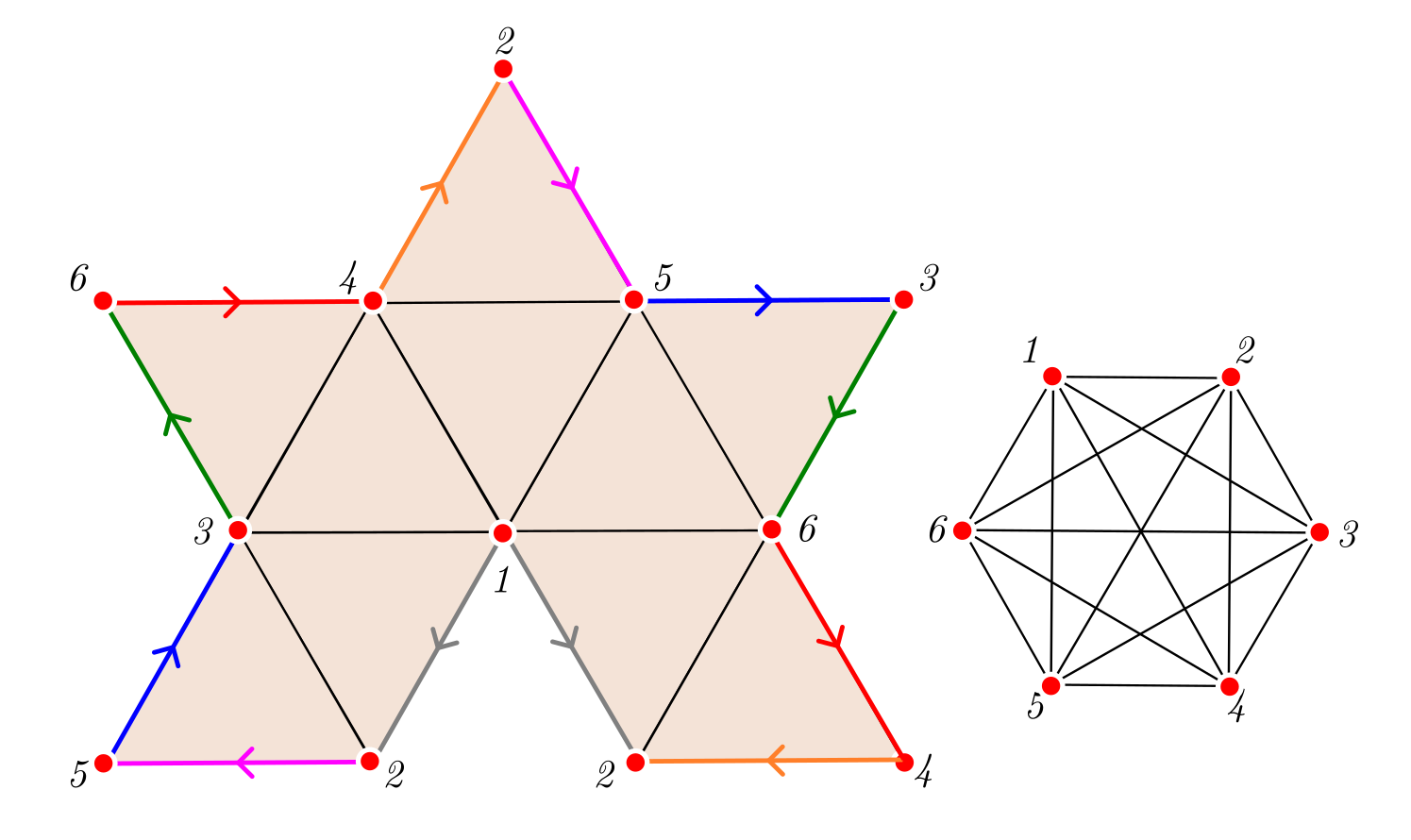
Развёртка полуикосаэдра и соответствующий ей граф Е₆. Одинаковым цветом показаны отождествляемые отрезки.
Существует несколько различных погружений проективной плоскости в трёхмерное евклидово пространство. Для демонстрации множества из шести равноудалённых точек годится то, что называется римской поверхностью. У неё подходящая симметрия и хорошая параметризация, хоть и не обеспечивающая изометричности развёртке.

Опять же, чтобы не перегружать иллюстрацию вместо полного графа я показал только те рёбра, которые на развёртке обозначены чёрным цветом.
Последние замечания
Рассмотренные поверхности можно поделить на два класса: «свободные» и «фиксированные». На свободные не накладывается никаких ограничений: на любой сфере можно разместить четыре эквидистантные точки. Это же относится и к проективной плоскости и к неограниченному цилиндру. В то же время, тор, бутылка Клейна, конус и лента Мёбиуса должны иметь определённые пропорции, для того, чтобы иметь возможность вместить максимальное для своей топологии число равноудалённых точек.
Конечно же, рассмотренную задачу можно решить тривиальным способом. Например, желая на некоторой развëртываемой поверхности расположить, скажем 7 точек, можно просто нарезать одинаковые бумажные ленточки и с помощью степлера или клея соорудить из них полный граф с семью вершинами и 21 ребром. При этом получится огромное количество дырок и эта поверхность будет в известном смысле, избыточной. Она не может уже быть непрерывно отображена на плоскость из‑за дырок, и как‑либо параметризована. К тому же, опять же, из‑за многочисленных дырок, у такого множества равноудалённых точек нет никакой свободы в перемещении по полученному пространству, кроме самых незначительных. Оно в этом смысле самое жёсткое. За исключением конуса, все приведённые выше примеры позволяют свободно перемещать полученные множества по двумерным поверхностям в двух измерениях, с сохранением их ключевого свойства: эквидистантности.
