Собеседования по алгоритмам: максимальная конкатенация26.06.2023 03:46

Чему равно самое большое число, которое можно составить из следующих карточек?

Если бы числа на карточках были однозначные, то всё было бы совсем просто: мы бы просто упорядочили их по убыванию. Например, самое большое число, которое можно составить из карточек »2»,»3»,»9» — это 932.

Когда же на карточках числа могут быть произвольной длины, то решение придумать становится сложнее, но при этом есть такое же простое решение! (И соответствующий алгоритм можно реализовать в одну строчку!)

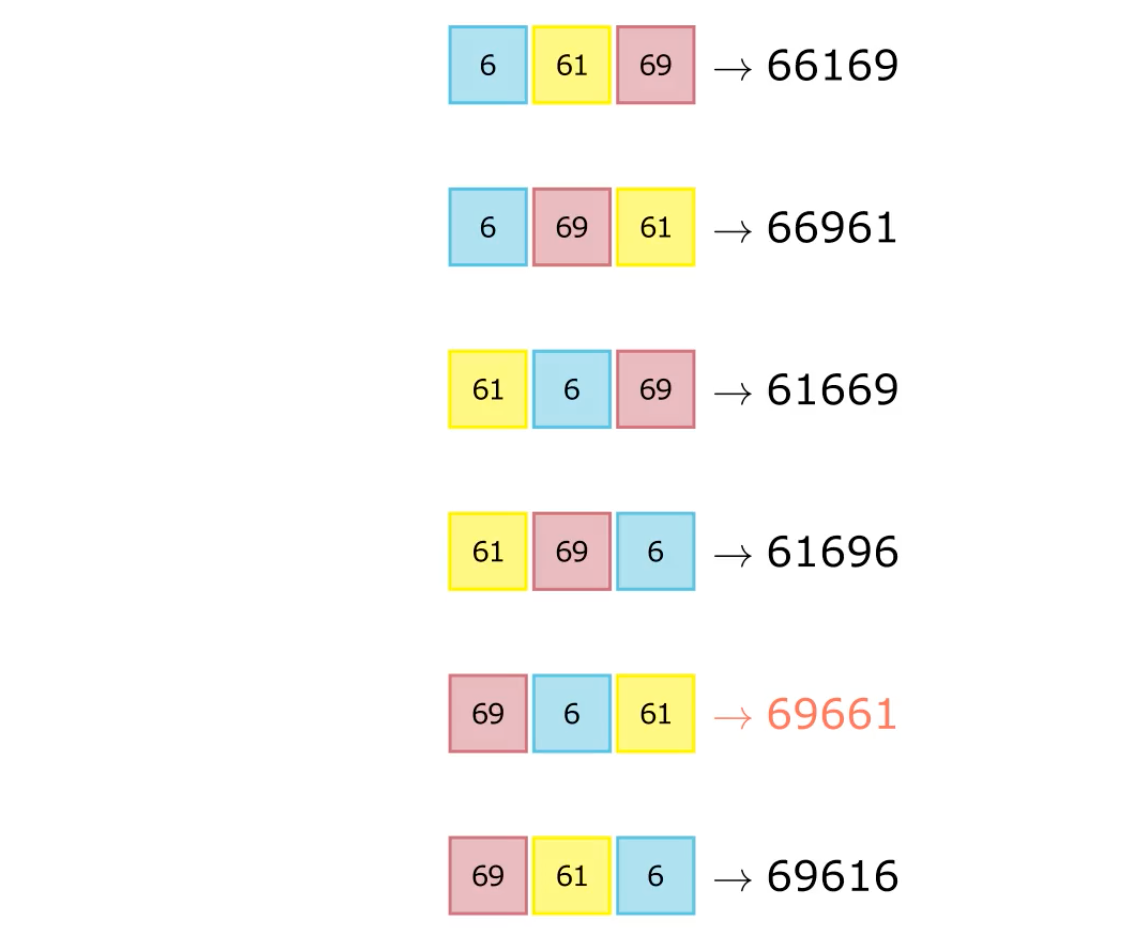
Как это часто бывает в алгоритмах, первым делом полезно придумать наивный алгоритм. В нашем случае — это просто перебор всех перестановок. Например, для чисел »6»,»61»,»69» он выдаст нам ответ 69661.

from itertools import permutations

xs = ['6', '61', '69']
print(max(''.join(p) for p in permutations(xs)))

Если чисел мало, то этот код отработает быстро. Но с ростом , количества входных чисел, этот алгоритм быстро станет непрактичным, потому что количество перестановок есть , а растёт непозволительно быстро.

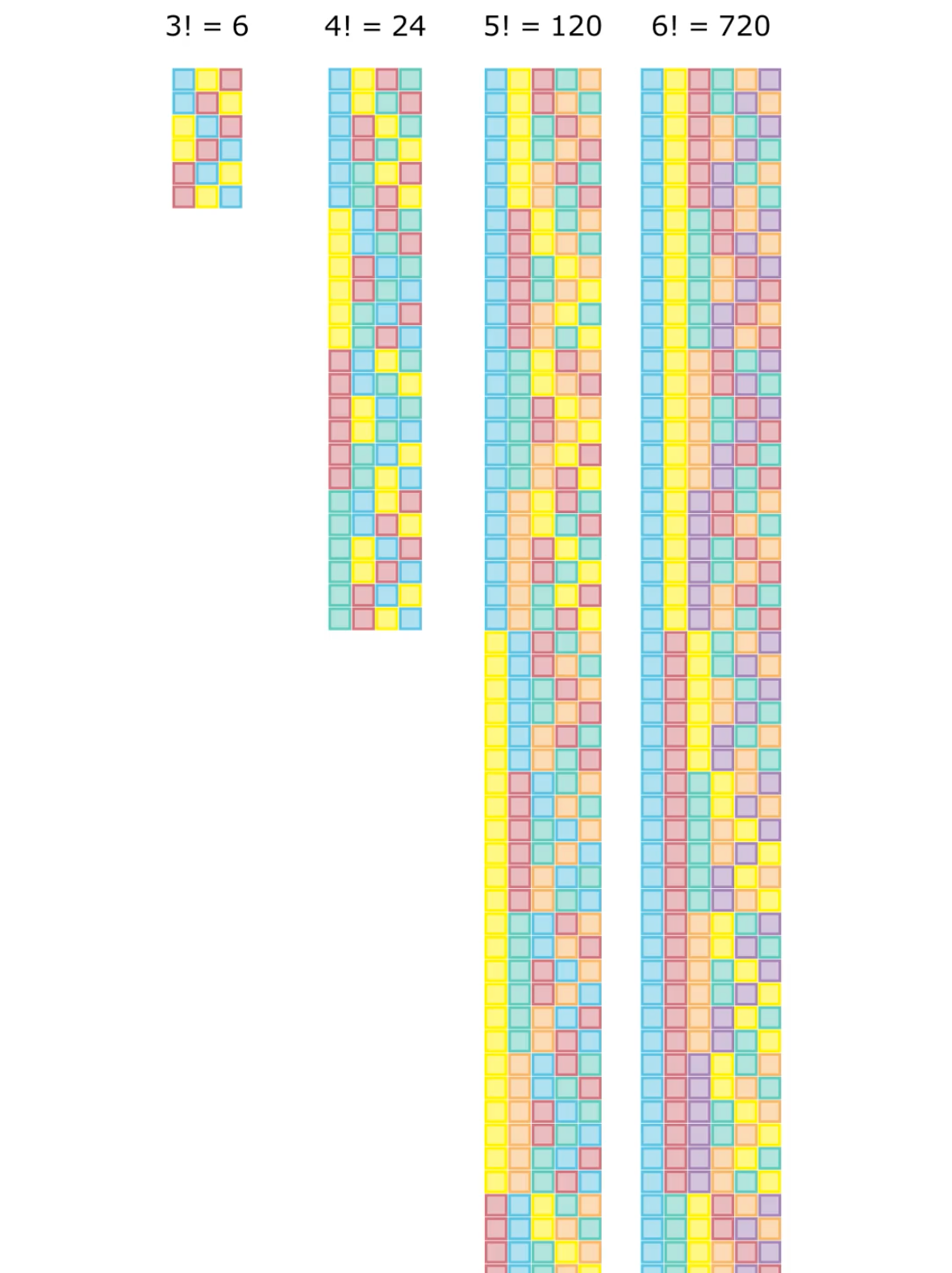
Например, если перебирать перестановки со скоростью 10^9 штук в секунду, то на перебор всех перестановок двадцати объектов понадобится $\frac{20!}{10^9 \times 60 \times 60 \times 24 \times 365} \approx 77$ лет.

Можете вручную найти ответ для пяти карточек из шапки поста? И можете написать программу, которая за секунду обработает сто карточек?