Сингулярность, желе и математика: делаем робота для реабилитации после инсульта02.05.2022 12:46

Привет, Хабр! Сегодня мы позвали в наш блог Валерию Скворцову — ассистента Лаборатории робототехники Университета Иннополис, чтобы она рассказала о разработке научного прототипа робота для реабилитации кистей рук при парезах, вызванных, например, инсультом. Робот спроектирован по принципу параллельного сферического манипулятора, и хотя проект еще не завершен, там уже есть на что посмотреть. Передаем ей слово.

Начну с начала. Можно сказать, что идею этого проекта подсказали преподаватели, когда я училась робототехнике на первом курсе магистратуры Университета Иннополис. Для курсовой работы по Introduction to Robotics предложили тему «Робот для реабилитации кисти руки». Я заинтересовалась и, так как разбираюсь в промышленном дизайне, решила сделать из курсовой диплом. Проект затянулся, я занималась разработкой всю магистратуру, получила грант «Умник» на развитие инновационного проекта и продолжаю совершенствовать конструкцию.

Проблема реабилитации важна, потому что каждый год в России регистрируется около 450 тысяч инсультов головного мозга. Эта болезнь часто приводит к нарушению двигательной активности, парезам — состоянию, когда резко ослабевает сила мышц. К сожалению, полностью восстанавливаются лишь около 10% пациентов.

При этом реабилитация при парезах — это регулярные тренировки, во время которых пациент заново учится двигаться, постепенно восстанавливает старые нейромышечные связи и формирует новые. Проблема в том, что специалистов по реабилитации не хватает, однако в ряде случаев для помощи пациентам применяют роботов.

Роботы для восстановления подвижности кистей рук уже существуют, их активно используют в США и Швейцарии. Пациент помещает руку в такой аппарат, его локтевой сустав фиксируют на специальной подставке, а затем подвижные элементы машины разрабатывают запястный сустав: плавно двигают кисть вниз и вверх, вправо и влево и скручивают в обе стороны. Я хотела сделать нечто подобное.

Старт разработки

Прежде всего нужно было выбрать тип конструкции. В процессе анализа литературы в одной из диссертаций нашлась модель параллельного сферического манипулятора. Я решила взять эту идею за основу и рассчитать кинематику под мою задачу.

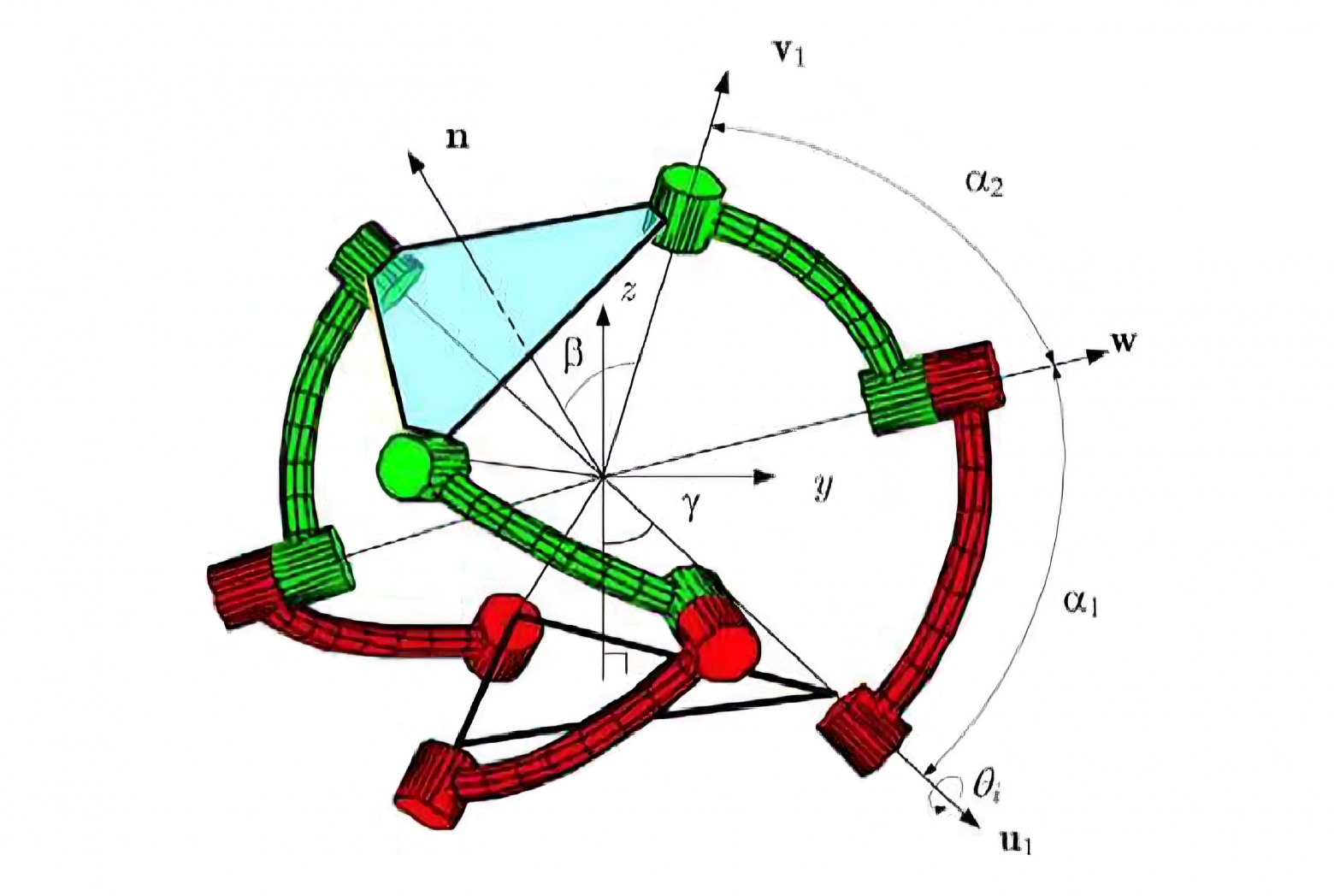Красным и зеленым обозначены шесть плеч робота. Красные и зеленые плечи в связке образуют три ноги. Закрашенный треугольник — так называемая мобильная платформа Красным и зеленым обозначены шесть плеч робота. Красные и зеленые плечи в связке образуют три ноги. Закрашенный треугольник — так называемая мобильная платформа

Человеческая кисть, если зафиксировать руку в локтевом суставе, описывает в пространстве некую полусферу.

Параллельный сферический манипулятор так же, как и запястный сустав, имеет три вращательные степени свободы. Поэтому его использование для реабилитации кисти руки оправданно с физиологической точки зрения. А если спроектировать манипулятор так, чтобы фиксированный центр вращения совпадал с центром вращения кисти руки, робот сможет повторять ее движения во всем доступном человеку диапазоне. Кроме того, параллельная конструкция компактнее и обеспечивает большую жесткость, чем последовательные манипуляторы.

По сравнению с решениями для реабилитации, которые уже есть на рынке (с готовыми продуктами, а не другими научными разработками), это значительные преимущества.

Тренажер Kinetec Maestra hand and wrist CPM (слева) и Аппарат АРТРОМОТ Н (справа)

Готовые коммерческие системы обладают одной, максимум двумя осями и не могут одновременно двигаться в трех степенях свободы и потому менее эффективны.

Расчет кинематики

Процесс разработки был итеративным и первое время даже хаотичным, поэтому его трудно разделить на последовательные этапы.

Я рассчитывала кинематику и сразу проверяла на простых механических моделях, распечатанных на 3D-принтере. Сначала без моторов, потому что прежде всего меня интересовала геометрия деталей.

Если что-то не получалось, плечи робота застревали или двигались не так, как я рассчитывала, приходилось пересчитывать кинематику и печатать модель заново. Все-таки конструирование робота — это больше математическая, а не чисто инженерная задача.

Вы не сможете точно управлять движениями робота, если не решите задачу обратной кинематики. Для этого мы выбираем желаемую ориентацию робота в пространстве и рассчитываем углы поворота моторов, которые помогут достичь этого положения.

Прямая кинематика представляет собой обратную задачу — вычисление того положения, в котором окажется робот, если моторы будут повернуты определенным образом. В моем проекте прямая кинематика используется для проверки правильности выполнения команд.

Решение дифференциальной задачи кинематики помогает управлять скоростью и силой, с которой движется манипулятор. Эти расчеты важны для безопасности пациента: если что-то пойдет не так, то робот может повредить его руку.

За всем этим скрываются сложные математические задачи. Вот, например, некоторые расчеты для обратной кинематики.

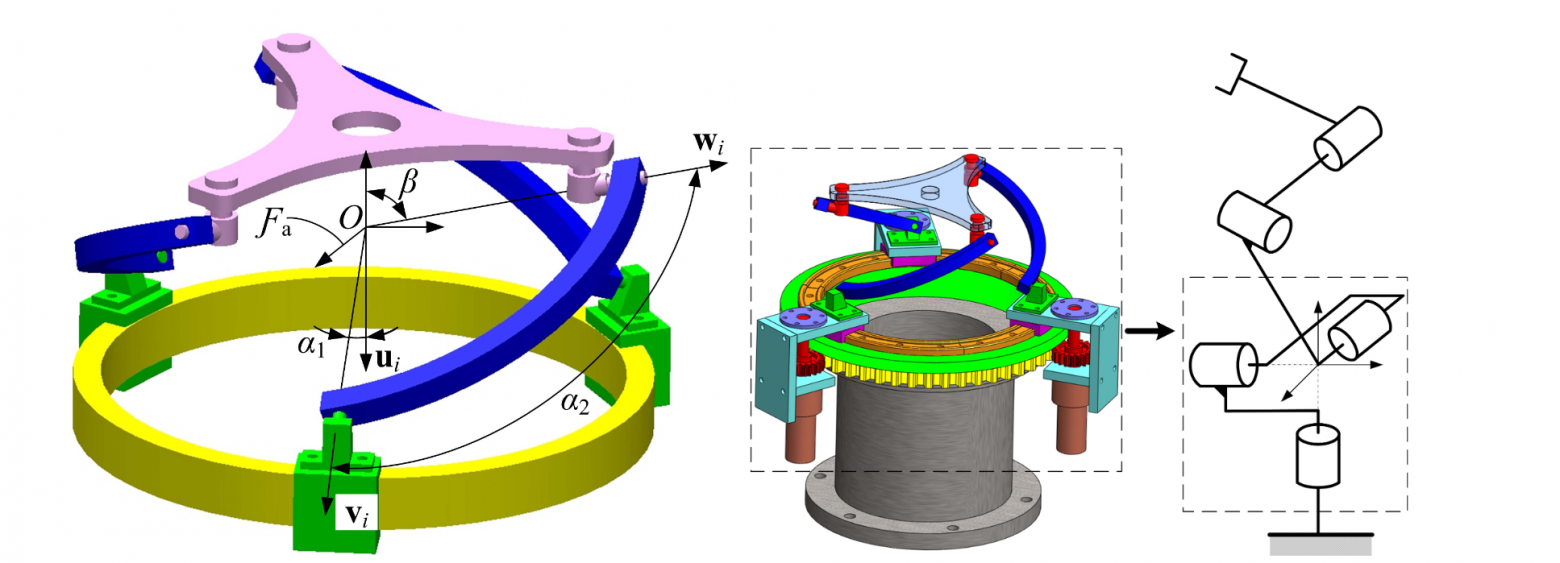
С математической точки зрения параллельный сферический манипулятор описывается двумя виртуальными пирамидами, стоящими друг на друге. Центр вращения робота находится в точке О, это точка соприкосновения вершин двух пирамид. Набор углов [β_1 β_2 α_1 α_2 ]^T определяет механические свойства, не изменяется в процессе работы и определяет рабочее пространство робота.

Углы β_1 и β_2 определяют положение центра вращения и угол крепления ног к базовой и мобильной платформам соответственно, а углы α_1 и α_2 определяют длины дуг опорных плеч, из которых состоит каждая нога робота.

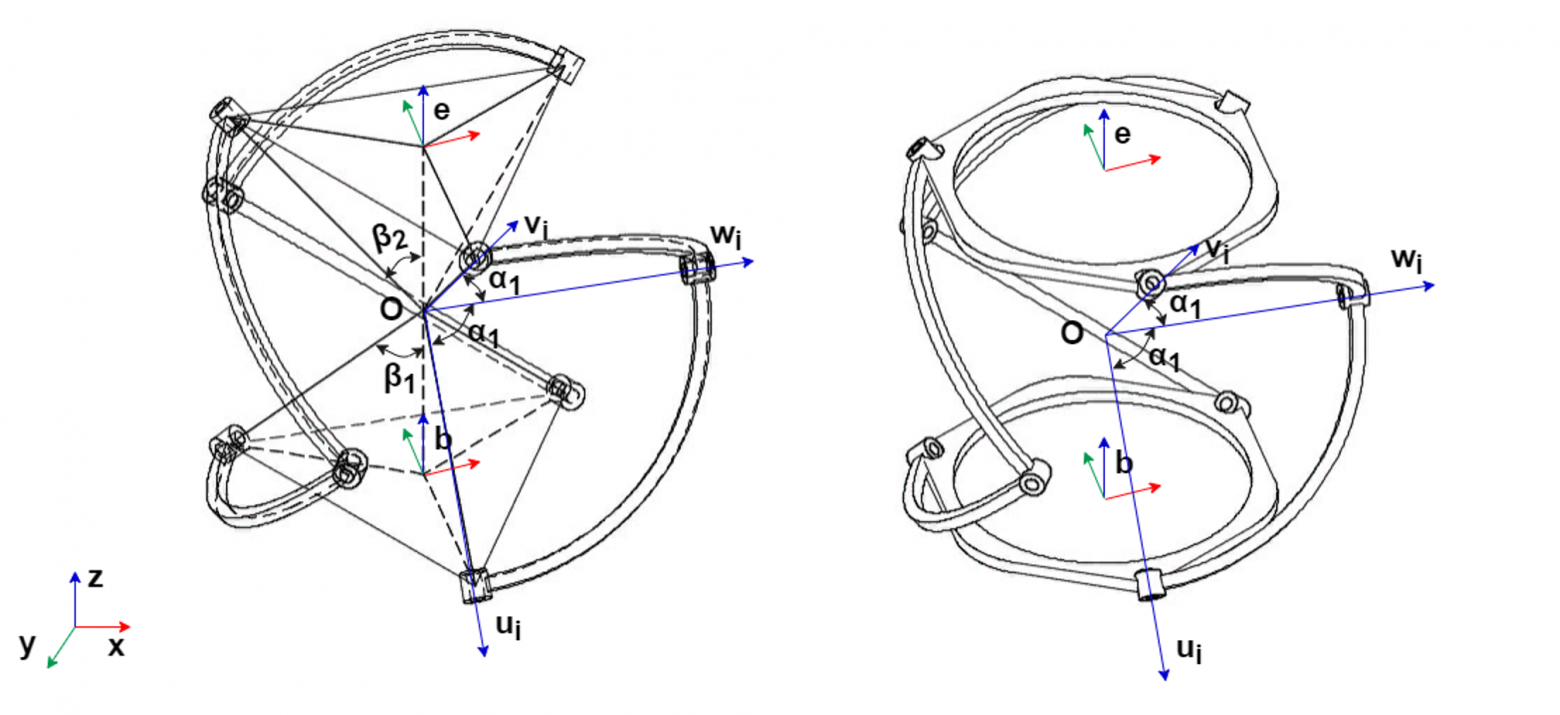Схема систем координат параллельного сферического манипулятора

Для вычисления углов в нижних суставах опорных плеч используется скалярное произведение для z-векторов v и w систем координат в каждой из ног. Их скалярное произведение должно быть равно косинусу дуги опорного плеча между ними:

$\textbf{v}_i(z) \cdot \textbf{w}_i(z) = \cos(\alpha_2)$

В этом уравнении можно провести следующую замену:

$\sin(q_{1i})=\frac{2T}{1+T^2}; \quad \cos(q_{1i})=\frac{1-T^2}{1+T^2}$

Получается простое квадратное уравнение:

$A_{q_{1i}}T^2+B_{q_{1i}}+C=0$

Это означает, что решением для q_1i будет решение данного квадратного уравнения и его дальнейшее преобразование через арктангенс:

$q_{1i}=2\arctan(T)$

Чтобы вычислить углы в средних суставах между опорными плечами в ноге, используется следующее уравнение:

$\textbf{e}(z) \cdot \textbf{v}_i(z) = \cos(\beta_2)$

Для вычисления углов q_2i проводится тот же набор операций, только относительно угла q_1i .

Борьба с сингулярностью

Еще одна сложность связана с сингулярностью. Нет, не с тем моментом, когда нас поработит искусственный интеллект. В сингулярных состояниях робот испытывает очень высокую нагрузку на суставы либо его движение блокируется. Такие состояния есть у всех роботов, но проще объяснить суть проблемы на примере человеческого тела.

Когда вы приземляетесь после прыжка, безопаснее согнуть ноги, потому что если они будут выпрямлены, то коленный сустав может вывернуться и получится вывих. Можно сказать, что вытянутая нога находится в сингулярном состоянии. Это справедливо и для полностью вытянутой роборуки. Если подать команду на движение, нельзя будет предсказать, в какую сторону повернется рука относительно своих осей.

Для параллельных роботов существует три типа сингулярных состояний. Первый тип относится к последовательной части структуры робота и называется последовательной сингулярностью. Она возникает, когда мобильная платформа неподвижна, а активные суставы имеют ненулевую скорость.

С точки зрения математики это происходит тогда, когда матрица Якоби хотя бы одной из ног вырождается и приобретает линейную зависимость.

Второй тип сингулярности называется параллельной сингулярностью. В общей форме Якоби для робота используется оператор псевдоинверсии:

${q}_{pass}=g {q}_{act}; \quad g=\left[\begin{array}{c}g_1 \\ g_2 \\ \vdots \\ g_m \end{array}\right]=-J_{pass}^+J_{act}$

В этом операторе присутствует обратная матрица из J_pass^T J_pass . Если эта матрица вырождается, то получить ее обратную матрицу невозможно. Соответственно, ориентация робота, соответствующая этой матрице, является параллельно-сингулярной.

Физически в таком состоянии будет ненулевой поворот мобильной платформы, для которого скорости в активных суставах равны нулю. В окрестностях такой конфигурации робот может иметь бесконечно малейшие движения при заблокированных исполнительных элементах. В результате одна из степеней свободы мобильной платформы не поддается управлению.

Последний тип называется смешанным типом сингулярности. Это суперпозиция между первыми двумя типами (последовательная и параллельная сингулярность выполняются одновременно). В результате мобильная платформа перемещается в пространстве, когда исполнительные механизмы заблокированы, и наоборот.

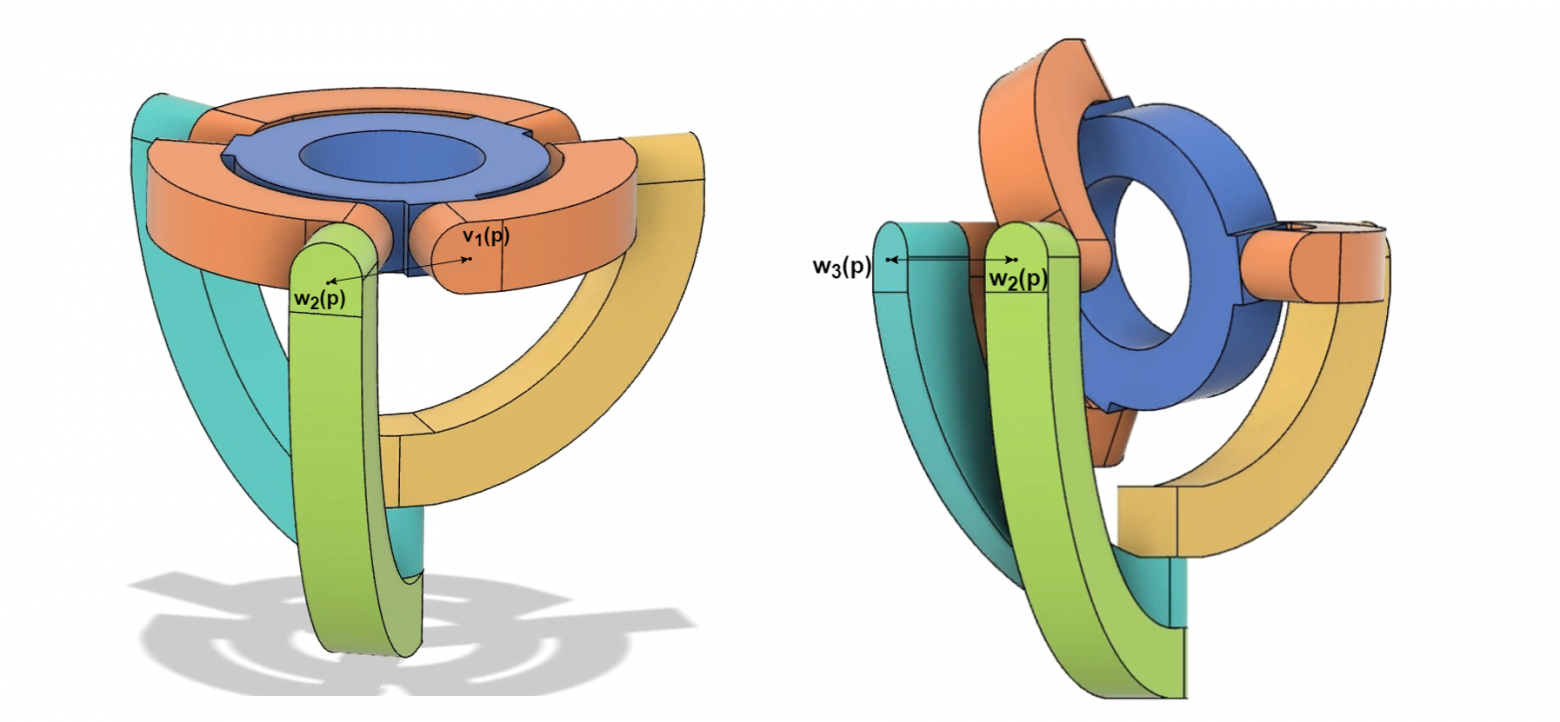Коллизии параллельного сферического манипулятора при 1=0. Между нижним опорным плечом и верхним опорным плечом (слева) и между нижними опорными плечами (справа)

Чтобы определиться с окончательной конструкцией, нужен был тип манипулятора, в котором сингулярность будет меньше, то есть я должна была решить задачи оптимизации для классического и асимметричного манипуляторов.

Модели прототипов параллельного сферического манипулятора в классическом исполнении (слева) и асимметричном исполнении (справа)

В классическом исполнении робота активные суставы находятся в месте соединения ног с базовой платформой, что на рисунке 1 соответствует u системам координат. Соответственно, набор активных и пассивных суставов в этом исполнении может быть описан набором векторов:

$q_{act(v_1)}=\left[\begin{array}{ccc} q_{11} & q_{12} & q_{13} \end{array}\right]^T; \quad q_{pass(v_1)}=\left[\begin{array}{cccccc} q_{21} & q_{31} & q_{22} & q_{32} & q_{23} & q_{33} \end{array}\right]^T$

В асимметричном манипуляторе три активных сустава находятся в месте соединения опорных плеч каждой ноги робота, что соответствует w системам координат, и один из двигателей находится в основании первой ноги. В этом случае набор активных и пассивных суставов можно описать так:

$q_{act(v_2)}=\left[\begin{array}{cccc} q_{11} & q_{21} & q_{22} & q_{23} \end{array}\right]^T; \quad q_{pass(v_2)}=\left[\begin{array}{ccccc} q_{31} & q_{12} & q_{32} & q_{13} & q_{33} \end{array}\right]^T$

Мне нужно было выбрать тип манипулятора, в котором сингулярность будет меньше, то есть решить задачи оптимизации для обоих типов манипуляторов.

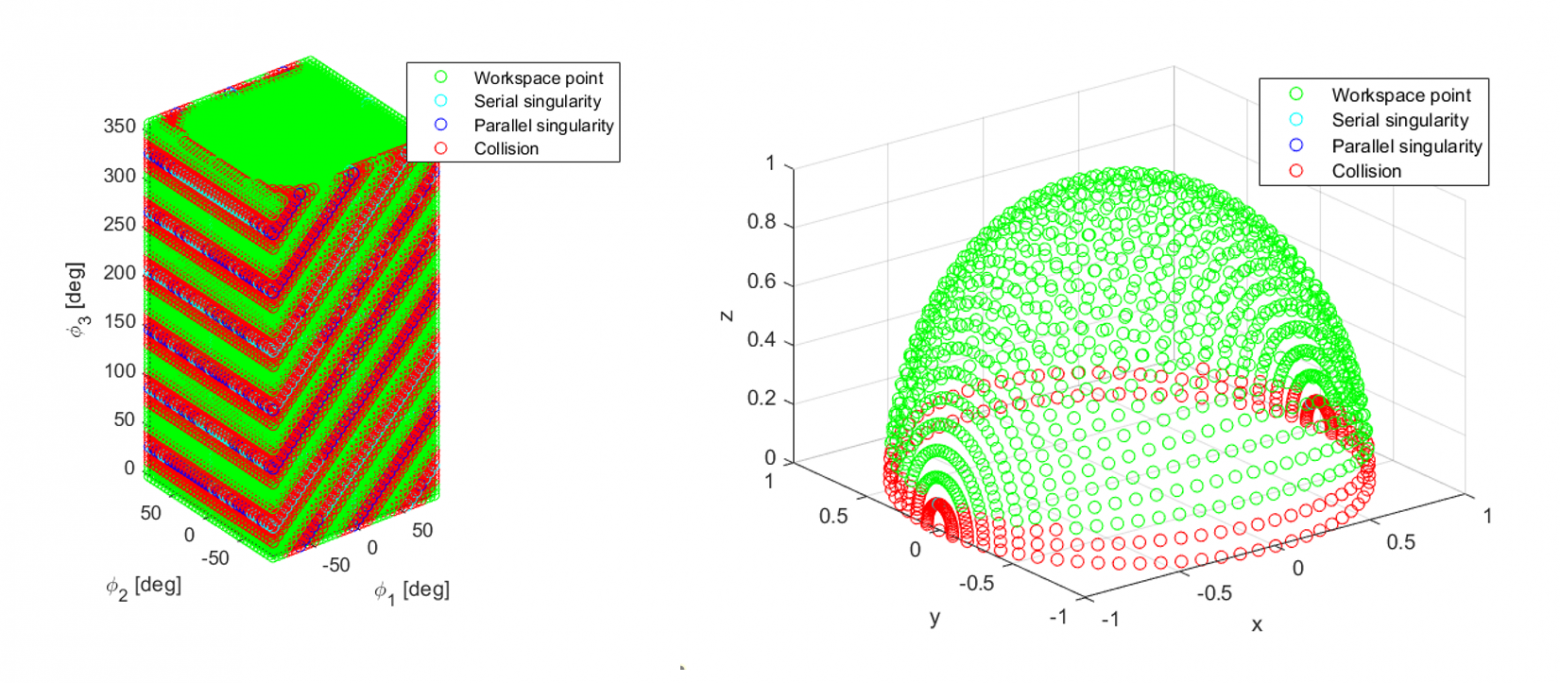
Рабочее пространство классического исполнения параллельного сферического манипулятора с параметрами

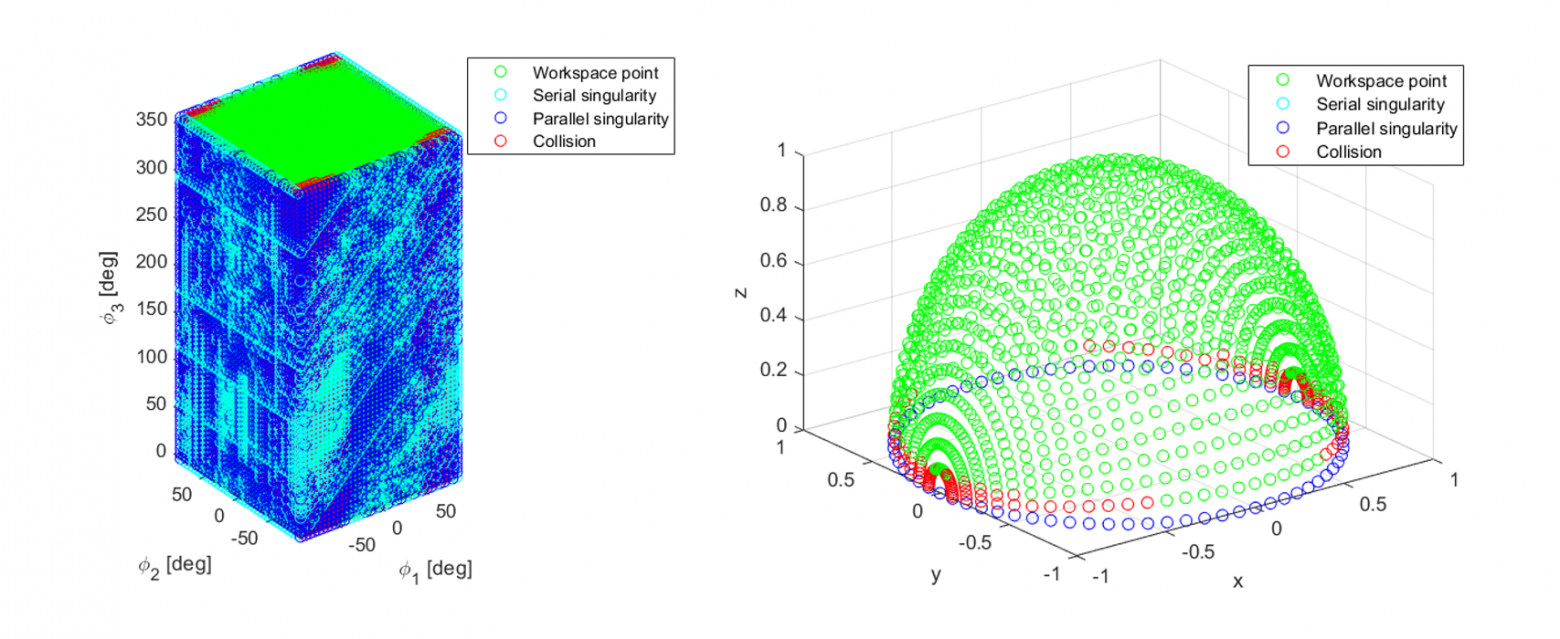
Рабочее пространство асимметричного исполнения параллельного сферического манипулятора с параметрами

Моделирование показало, что асимметричное исполнение выигрывает у классического в рабочем пространстве при β_1=0 , так что выбор пал именно на эту конструкцию.

Математическая модель и визуализация в MATLAB

Все расчеты я производила в MATLAB. Там же написала простой визуализатор, в котором оси вращения соединены отрезками с системами координат, переходами и так далее, чтобы визуально можно было оценить верность тех или иных решений. Получился 3D-график того, как все детали располагаются в пространстве.

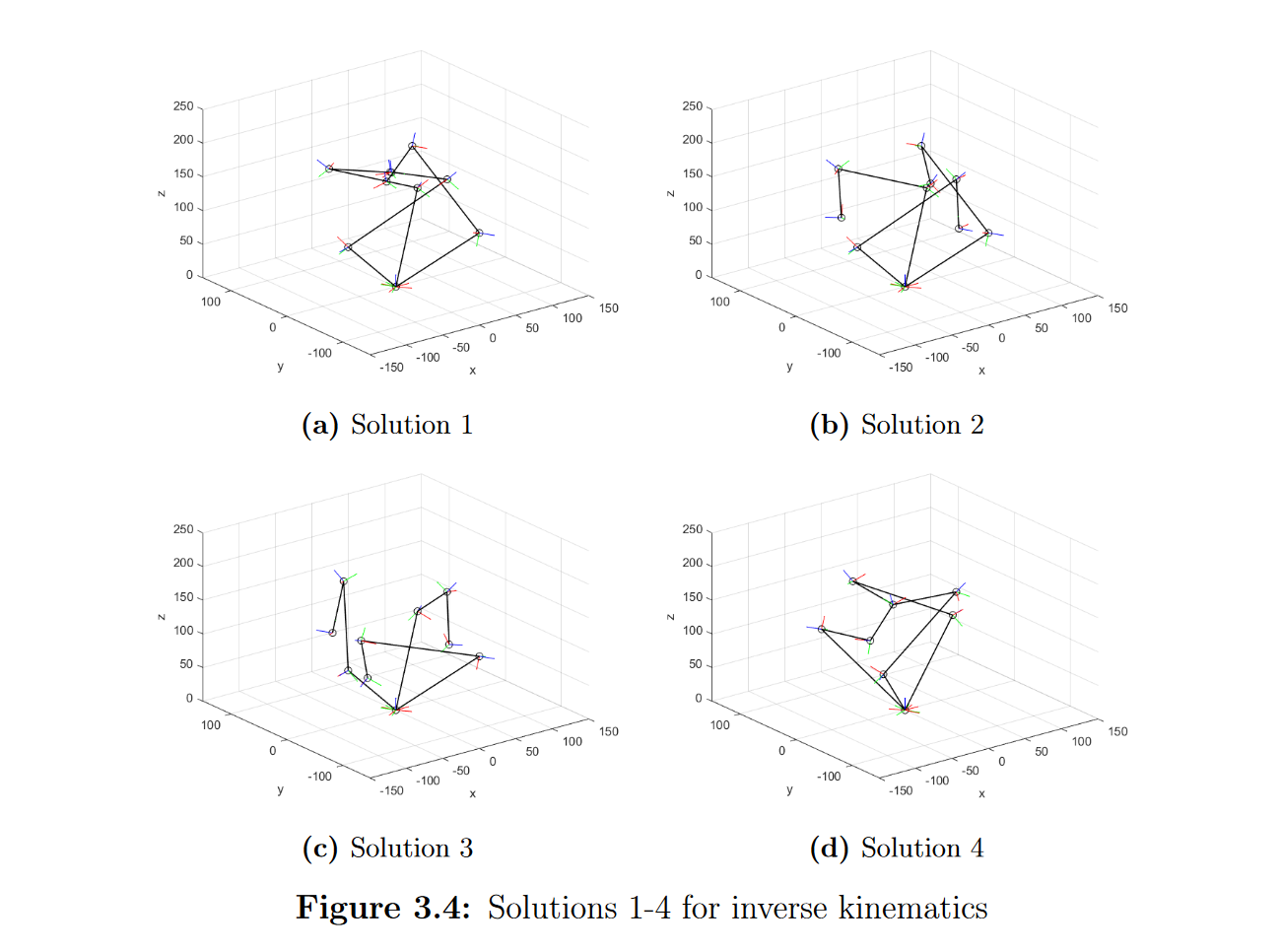
Особенность прямой и обратной задач кинематики параллельных роботов в том, что если все правильно, то все три ноги робота должны сходиться в одной точке. Поэтому даже такого простого визуализатора достаточно для валидации расчетов.

Сборка робота

Моторы для первого прототипа, подшипники, соединительные элементы и прочее я подбирала методом проб и ошибок и занимаюсь этим до сих пор. Строго говоря, просчитать и подобрать все детали — очень большая работа, на которую вечно не хватает времени.

Однако, научный прототип — это не законченный рыночный продукт, который полностью обсчитан и испытан. В научной разработке некоторыми вещами можно пренебречь, потому что задача — не продать робота, а проверить гипотезу, выяснить имеет ли она право на существование или нет.

Первоначально я печатала ноги и оси робота из нейлонового филамента. Я выбрала его из-за хороших показателей прочности, особенно на разрыв, но вскоре выяснилось, что деталям из этого материала не хватает жесткости.

В результате первый полноразмерный прототип вел себя как желе. Чтобы он хоть как-то работал, пришлось вставлять металлические спицы между ногами робота. Это позволило увеличить жесткость конструкции без значительного увеличения веса.

Сейчас мы с коллегами осваиваем лазерную резку металла. Это довольно дешевая технология, и с ее помощью можно добиться хороших результатов по жесткости.

Управление и программное обеспечение

В выбранные мной двигатели DYNAMIXEL MX-106 встроен драйвер с базовой системой управления по позиции, скорости и току. Они поддерживают протокол RS-485, имеют открытый исходный код и API для различных языков программирования. Для управления ими даже не понадобились микроконтроллеры. Я повесила моторы на одну последовательную шину и подключила на преобразователь напрямую в USB.

Обновленный прототип с большей жесткостью

Для тестирования прототипа я сначала пользовалась языком программирования MATLAB, потому что он часто используется в научной среде, достаточно прост и не требует глубоких знаний программирования. Но задачи постепенно усложнялись, и пришлось переходить на C++ и Phyton. Думаю, что в следующей реализации верхний уровень управления (траектории и UI) будет написан на Python, а нижний (опрос датчиков и управление моторами) — на C++.

Будущее проекта

Прототип робота получил базовую ось, с помощью которой он жестко крепится к поверхности, например к столу. Моторы установлены на нижних ногах, но около года назад в одной из статей про параллельные сферические манипуляторы я увидела реализацию подобного робота без оси и ног. В этом варианте моторы двигаются на подшипниках по окружности.

Траектории остаются прежними, но такая конструкция занимает меньше места. Сейчас я работаю над ее реализацией. Основная задача — уменьшение трения кареток на дуге, где располагаются моторы.

Прежде чем робота можно будет испытывать на людях, придется поработать над обратной связью. Сейчас я проверяю положение манипуляторов по данным с моторов, но этого недостаточно, так можно повредить пациенту руку. Коллеги в шутку предлагали установить микрофон, чтобы определять момент, когда пациент закричит, но, если серьезно, роботу необходимы специальные датчики.

Идеальный вариант — неинвазивные датчики, которые измеряют уровень напряжения в мышцах. Их применяют в экзоскелетах, но доступные образцы выдают очень шумные данные. Скорее всего, я сперва попробую датчики силы.

Есть исследования, которые говорят о том, что элементы геймификации повышают эффективность реабилитационных процедур, так как увеличивают вовлеченность пациента. Возможно, когда-нибудь я добавлю их в свой проект, но до этого еще далеко. Сперва необходимо запатентовать модель кинематики, завершить новый прототип, настроить податливое управление и организовать испытания на людях.

Впереди terra incognita, но у меня есть ясная цель — помочь людям, а опыт таких проектов, как ЭкзоАтлет, показывает, что это возможно.