Символ Шлефли. Часть 2.6
Хабрахабр, уважаемые коллеги! Когда смотрю на соты, то думаю не о пчёлах, а о Символе Шлефли. Прочитав эту статью, вы уже не сможете смотреть на мир по старому, вы поймёте, что между сотами и правильными многогранниками есть прямая связь. По опыту разъяснения друзьям вывода правильных многогранников в четырёхмерном пространстве и пространствах высших размерностей, оказывается, что мало кто знает, что такое Символ Шлефли, поэтому решил посвятить этому отдельную статью с картинками, без аналитических вычислений, которые делаются в других статьях, при непосредственном выводе многогранников. Понятие Символа Шлефли будем осваивать от лёгкого к трудному. Самое простое на плоскости.
Как устроен квадрат? Ответ: из четырёх одинаковых сторон. Символ Шлефли {4}
Как устроен правильный девятиугольник? Ответ: из девяти одинаковых сторон. Символ Шлефли {9} Смотрите рисунок:
Правда элементарные вопросы? Давайте в обратную сторону, как называется правильный многоугольник из десяти одинаковых сторон, Символ Шлефли {10}?
Итак, самое простое всё-таки, это Символ Шлефли для двухмерного пространства. Обозначение {p1}, где p1 — целое число большее либо равное 3, просто потому, что двухугольников не бывает, в привычном нам смысле. Число p1 при этом показывает количество рёбер правильного многоугольника (двумерного многогранника), смотрите рисунок выше.
Вроде бы всё очевидно, {3} — правильный треугольник, {4} — квадрат, {9} — правильный девятиугольник, и так далее.
На плоскости — это первый шаг понимания Символа Шлефли, надеюсь понятна связь символа и строения многоугольника, сделаем второй шаг на пути к трудному, — для трёхмерных правильных многогранников ответы на вопросы о строении этих многогранников тоже даёт Символ Шлефли. Т.е. Символ Шлефли обобщает понятие числа сторон правильного многоугольника на правильные многогранники.
А именно: Как устроен Куб?
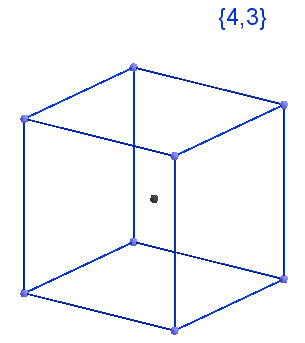Куб это {4, 3}, это его Символ Шлефли, который означает, что он состоит из 4-рёхугольников, сошедшихся по 3 штуки в вершине. Рисунок слева.Т.е. куб получается соединением 3-х квадратов {4}, в каждой вершине. Склейка в одной из вершин показана на видео.
Видео записано под операционной системой Ubuntu, программа записи называется recordmydesktop.
Аналогично своими Символами Шлефли задаются остальные четыре правильных многогранника.
Как устроен Октаэдр?
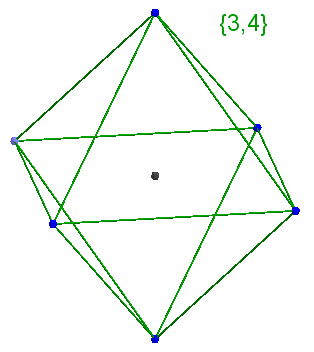{3, 4} — Символ Шлефли, который означает, что октаэдр состоит из 3-угольников, сошедшихся по 4 штуки в вершине.Как устроен Икосаэдр?
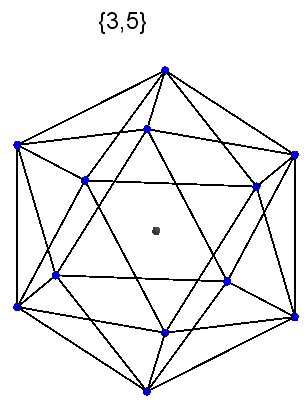{3, 5} — Символ Шлефли, который означает, что Икосаэдр состоит из 3-хугольников, сходящихся по 5 штук в вершине.Давайте в обратную сторону, какую фигуру означает Символ Шлефли {3, 3}, 3-хугольники сошедшиеся по 3 в вершине?
тетраэдрКакую фигуру означает Символ Шлефли {5, 3}, пятиугольники по три в вершине?
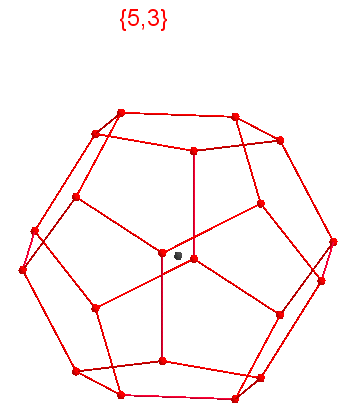ДодекаэдрВот и весь смысл Символа Шлефли в трёхмерии, для правильных многогранников. В трёхмерии мы можем пощупать правильные многогранники, показать наглядно на картинке, на видео, поэтому наше привычное трёхмерие, это лучшее пространство в котором можно хорошо понять суть Символа Шлефли. А когда этот рубеж будет преодолён, тогда будем углубляться, утрудняться.
Изначально у меня было большое желание напечатать правильные многогранники на 3D принтере, поэтому я начал осваивать бесплатную программу OpenSCAD по рекомендации одной статьи на Хабре.
При этом неожиданно удалось написать алгоритм, который по Символу Шлефли (т.е. по двум входным параметрам p1, p2) строит соответствующий правильный многогранник. Это здорово, что удалось сделать такой унифицированный алгоритм, это самостоятельный небольшой, интересный результат, при этом листинг умещается на одном экране, всего один оператор if и, главное, очень наглядно можно продемонстрировать смысл Символа Шлефли. Этим алгоритмом удалось показать, что строение правильного многогранника в трёхмерии зависит всего от двух параметров {p1, p2} смотрим видео ниже. При просмотре видео нужно выполнить задание, нужно посчитать сколько рёбер у двухмерных граней многогранников и сколько в вершине сходится двухмерных граней. Если вы выполните это задание, то загадка Символа Шлефли для вас навсегда будет раскрыта.
//Символ Шлефли {p1, p2}
/*
{3,3} - Тетраэдр
{3,4} - Октаэдр
{4,3} - Куб
{3,5} - Икосаэдр
{5,3} - Додекаэдр
*/
p1=5; //количество рёбер в двумерной грани
p2=3; //количество граней в каждой вершине
//точность прорисовки рёбер
accuracy=100;
//радиус описаной сферы
sphere_radius = 10;
//половина углового размера длины ребра
edge_angle_half = 90-asin(cos(180/p1)/sin(180/p2));
//половина длины ребра
edge_length_half = sphere_radius*sin(edge_angle_half);
//радиус описанной окружности грани
rb_face = edge_length_half/sin(180/p1);
//радиус вписанной окружности грани
rs_face = edge_length_half/tan(180/p1);
//угол подъёма грани по ребру
angle_up = 180-2*asin(cos(180/p2)/sin(180/p1));
//угол подъёма грани по вершине
angle_up1 = asin(sin(90-asin(cos(180/p1)/sin(180/p2)))/sin(180/p1));
//радиус вписанной в многогранник сферы
rs_polytop=sphere_radius*cos(angle_up1);
//высота пирамид из которых строится многогранник
ch=rs_polytop;
//ch=1; //для выдачи в печать
//difference() {
rotate([0, angle_up1, 0]){//поворачиваем модель так, чтобы одна из граней была параллельна оси Оху, чтобы печатать на 3D принтере
union(){
ten_edge();//прорисовываем нижнюю половину многогранника
if (!(p1==3 && p2==3)) rotate([0, 180, 0]) ten_edge();//прорисовываем верхнюю половину многогранника, у тетраэдра особенность, что вершины не лежат против друг друга, в отличие от других многогранников
}
}
//sphere(r=rs_polytop-0.3, $fn=accuracy);//вычитаем сферу, чтобы расход материалов на 3D печать уменьшился
//}
module ten_edge(){
translate([0, 0, -sphere_radius])
for (i=[0:1:p2])
rotate([0, -angle_up1, i*360/p2])/* поворачиваем на угол, чтобы в вершине сошлось p2 штук конструкций вокруг оси Oz, и конструкцию поднимаем на угол подъёма1, чтобы вершина многогранника осталась внизу */ translate([rb_face, 0, 0])/* сдвигаем конструкцию так, чтобы вершина первой грани попала в начало координат */
rotate([0, 0, (180/p1)*(1-p1+2*floor(p1/2))])/* для куба конструкцию нужно довернуть */{
union(){
rotate([0, 0, 180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);//рисуем первую грань, к ней по рёбрам подстыковываем столько граней, сколько рёбер у одной грани
translate([rs_face, 0, 0]) rotate([0, -angle_up, 0]) translate([rs_face, 0, 0]) rotate([0, 0, 180+180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);//вторые грани необходимо поднимать до нужного угла между гранями
}
}
}Рекомендую скачать OpenSCAD вставить туда исходники алгоритма и поиграться с многогранниками самостоятельно. Наиболее любознательным захочется вставить туда какие-нибудь другие числа. Напоминаю, кто забыл, что правильных многогранников в трёхмерии всего пять, поэтому на видео показаны все возможные варианты, для трёхмерия, других не бывает.
Следующий шаг утруднения состоит в том, чтобы ответить, что означают Символы Шлефли {4, 4}, {6, 3}, {3, 6}?
Подсказка: это не многогранники, это другие фигуры, визуально известные всем.
Теперь вы сможете ответить, что такое {6, 3}?
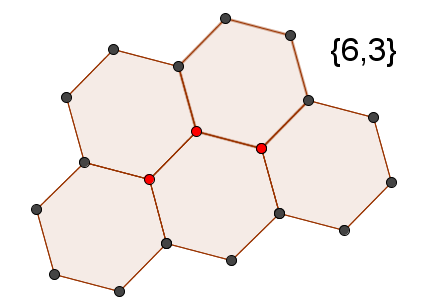СотыА что такое {3, 6}?
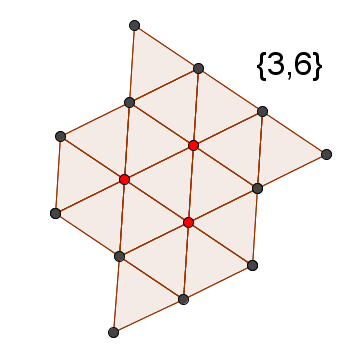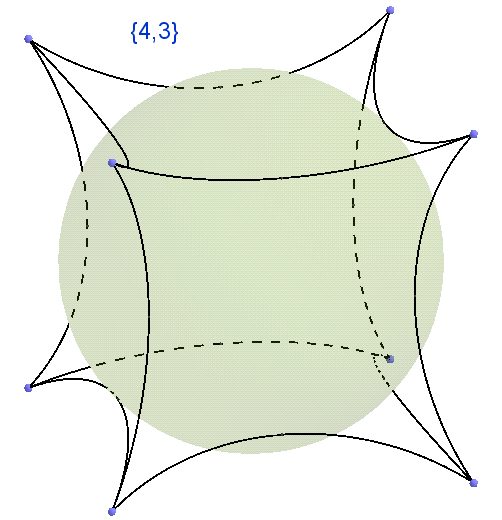
Красным выделены точки, в которых показаны все 6 сошедшихся треугольников, в остальных вершинах нужно продолжать рисовать, но продолжать можно до бесконечности, поэтому пришлось на чём-то остановиться.Ну вот, все три существующие РАЗБИЕНИЯ (с акцентом на слове РАЗБИЕНИЯ) плоскости Евклида мы рассмотрели, других нет, это было показано в статье Теперь когда вы держите тетрадь в клетку, то это не простые клеточки, это {4,4} разбиение плоскости Евклида; когда вы смотрите на соты, то вспомните, что это {6,3}. Уверен {3,3} тоже обязательно попадётся на глаза. Мы плавно от многогранников, которые обозначаются каждый своим Символом Шлефли, перешли к разбиениям плоскости Евклида, которые тоже обозначаются Символом Шлефли. Теперь следующий шаг (обобщения) утруднения в понимании Символа Шлефли состоит в том, что он задаёт РАЗБИЕНИЯ сферы. Так {3, 4} — это с одной стороны Октаэдр, с другой стороны это разбиения сферы на правильные сферические треугольники, сходящиеся по 4 штуки в вершине; {4, 3} — с одной стороны куб, с другой стороны это разбиения сферы на правильные сферические четырёхугольники, сходящиеся по 3 штуки в вершине. Более наглядно это показано на видео. Посчитайте количество двумерных граней и сколько таких граней сходится в вершинах.
Мы как бы надуваем многогранник (помещаем его на сферу), плоские грани при этом тоже раздуваются. Либо мы сдуваем его (помещаем его в пространство Лобачевского), плоские грани тоже сдуваются.
Т.е. Символы Шлефли задают целый класс фигур, т.к. любое изгибание рёбер без разрывов не изменяет Символа Шлефли, это показано на видео тем, что обозначение Символа Шлефли отображается на протяжении всей записи, при этом рёбра изгибаются, а Символ Шлефли остаётся прежним. На видео показаны специальные изгибания, при которых все углы фигур изменяются одновременно и одинаково.
Из всего класса фигур, задаваемых Символом Шлефли, в первую очередь нас интересуют три частных случая:
— когда Символ Шлефли задаёт правильный многогранник;
— когда Символ Шлефли задаёт разбиение сферы;
— когда Символ Шлефли задаёт разбиение пространства Лобачевского.
Эти и близкие к ним случаи показаны на видео выше. На видео показаны только куб и октаэдр, но дело обстоит ровно также и с остальными тремя правильными многогранниками {3,3}-Тетраэдр, {3,5}-Икосаэдр, {5,3}-Додекаэдр. С этого момента, когда мы начали говорить о разбиениях сферы, надо быть очень внимательным к размерности пространства в котором мы работаем. Дело в том, что поверхность сферы двумерна, а многогранники трёхмерны, но разбиения сферы и соответствующий разбиению многогранник обозначаются одним и тем же Символом Шлефли. Например, как было уже сказано, {3, 4} — октаэдр в трёхмерном Евклидовом пространстве, в тоже время {3, 4} — разбиения двумерной поверхности сферы на сферические треугольники, т.е. разбиение двумерного Сферического пространства. Что такое сферический треугольник интуитивно понятно, но кому хочется уточниться по этому вопросу можно прочитать в статье. Таким образом, когда говорим о Символе Шлефли задающим разбиение поверхности Сферы, то мы одновременно находимся в двух соседних размерностях пространств. В тоже время Символ Шлефли {3, 6} задаёт разбиения плоскости Евклида, т.е. разбиения Евклидовой плоскости тоже тут рядом.
Ну полнота картины и понимания смысла Символа Шлефли наступает, когда мы переходим к следующему шагу утруднения (обобщения) и начинаем говорить о РАЗБИЕНИЯХ плоскости Лобачевского. Не пугайтесь, нам достаточно базовых, интуитивных навыков работы с плоскостью Лобачевского, такие навыки даны в той же статье, где и про сферу, там же даны и картинки этих разбиений плоскости Лобачевского. Это не крайний шаг утруднения, но полнота наступает поскольку пространства Сферическое, Евклидово и Лобачевского — это все три пространства постоянной кривизны, других таких (с постоянной кривизной) пространств нет. Так Символ Шлефли {3, 6} задаёт разбиение плоскости Евклида, а {3, 7} задаёт разбиение плоскости Лобачевского. {3, 8}, {3, 9} и т.д. {3, p2} где p2 >= 7 — всё это разбиения плоскости Лобачевского на правильные треугольники. Таких разбиений бесконечное множество (счётное количество). Для примера приведу две картинки разбиений {3,7} и {5,4}, убедитесь, что в первом случае в каждой вершине сходится по 7 треугольников, а во втором по 4 пятиугольника.
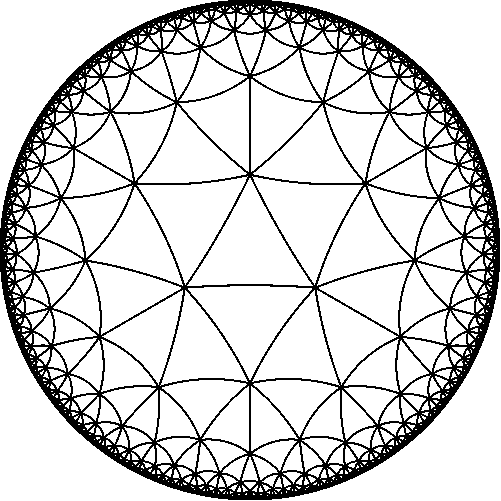
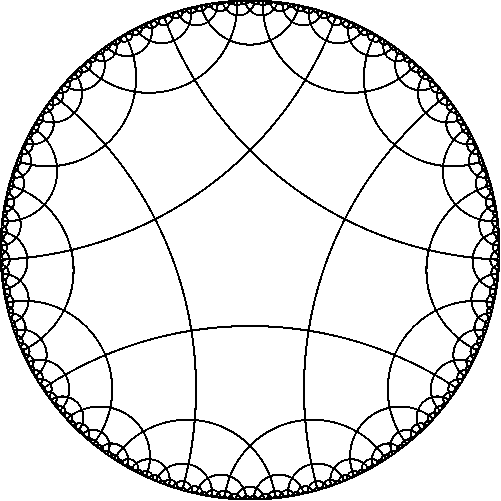
Для работы со Сферическим пространством и пространством Лобачевского достаточно образно представлять, что при помещении объекта на Сферу он «надувается», а при помещении в пространство Лобачевского он «сдувается».
Следующий шаг утруднения (обобщения) в понимании Символа Шлефли заключается в переходе в 4-мерное Евклидово пространство, которое по Символу Шлефли связано с разбиениями 3-мерного Сферического пространства, как аналогично было в размерности ниже, о чём мы уже говорили {4,3} — куб и разбиения сферы на сферические квадраты. Здесь уже сложнее рисовать картинки, включайте воображение, но постараюсь всё-таки кое-что нарисовать.
Первое, что необходимо понять, это переход от Символа Шлефли {p1, p2} к Символу Шлефли на размерность выше {p1, p2, p3}. Покажем переход от {4,3} к {4,3,4}. Так в трёхмерии {4, 3} четырёхугольники (плоские грани), склеиваются между собой по рёбрам (одномерные грани) и сходятся по 3 штуки в вершине (вершина — нульмерная грань). Аналогично для Символа Шлефли {p1, p2, p3}, например {4, 3, 4} — это тоже самое, что {{4, 3}, 4}, что означает, что кубы {4,3} (трёхмерные грани), склеиваются между собой по квадратам (двумерным граням), и сходятся в рёбрах (одномерных гранях) по 4 штуки в каждом ребре. Итак, что такое {4, 3, 4}? Кубы сошлись по 4 штуки в каждом ребре, что это? Подумайте, прежде чем открыть ответ.
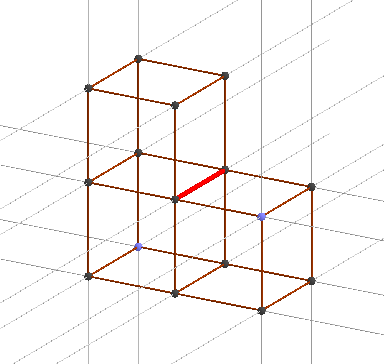
Это разбиение 3-мерного Евклидового пространства на кубы. Всё просто, это всем известный объект. Обратите внимание, что в рёбрах сошлось ровно по 4 куба, это показано на примере ребра выделенного красным. Число p3 в символе {p1, p2, p3} = {4, 3, 4} означает, что в ребрах сходится по p3=4 штук многогранников, а смысл чисел {p1, p2} остался прежним, который означает типы многогранников, сошедшихся в рёбрах.Итак, следующий шаг утруднения заключается в рассмотрении смысла символа {4, 3, 3}. Было разбиение 3-мерного Евклидового пространства на кубы {4,3,4}, но давайте один куб из ребра выкинем, получим {4,3,3}, что это такое в Евклиде?
Получилось не понятно что, это не разбиение, так как плоские грани кубов остались не заклеенными между собой. Что нужно сделать, чтобы они заклеились? Нужно надуть эти кубы, как мячики и надувать до тех пор, пока двумерные грани у кубов совпадут, вот тут-то мы их и склеим. Надуть — это образное выражение, в математике это называется поместить кубы (а они трёхмерные) на сферу, сделать кубы сферическими, аналогично тому как мы рассматривали сферические треугольники на двумерной сфере, только теперь кубы трёхмерные, значит и помещаем мы их на трёхмерную сферу. Сама сфера помещена в четырёхмерное Евклидово пространство, но поверхность у неё трёхмерна. Т.е. {4,3,3} разбивает трёхмерную сферу на кубы, сходящиеся по 3 штуки в ребре. 
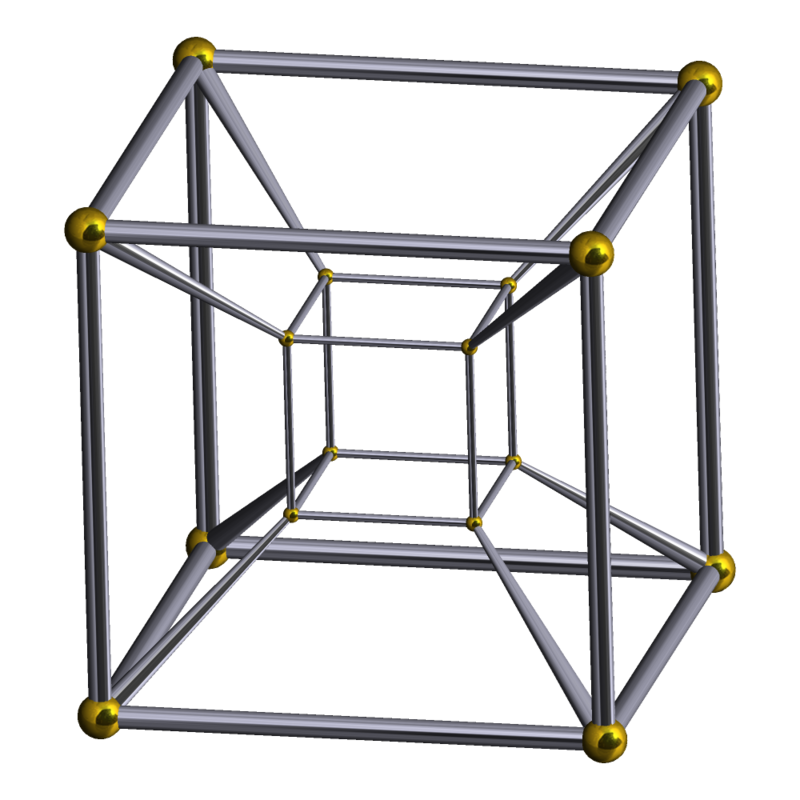Тяжело нарисовать четырёхмерие на плоскости, но народ уже научился это делать, обратите внимание как изогнуты рёбра (слева), это потому, что объект {4,3,3} на сфере, в данном случае означает разбиение трёхмерной сферы. Но ведь мы уже знаем, что разбиениям сферы соответствуют многогранники на одну размерность выше, чем поверхность сферы, значит {4,3,3} — это правильный многогранник в 4 мерном Евклидовом пространстве (справа), это Тессеракт, четырёхмерный куб. Почти тоже самое, только рёбра прямые стали, аналогично тому, как мы изгибали рёбра у трёхмерных многогранников, также можно изгибать рёбра у четырёхмерных многогранников, до получения нужного результата.Давайте ещё раз вернёмся к известному всем разбиению трёхмерного пространства Евклида на кубы сходящиеся по 4 в ребре {4,3,4}. Выше мы выбросили один куб до {4,3,3} и надули оставшиеся 3 куба до момента совпадения плоских граней кубов между собой. А что если начать сдувать имеющиеся 4 куба, разъединив в одном месте два соседние куба по плоским граням? Тогда останется зазор между этими гранями. Но сдувать можно и дальше, до тех пор, пока в этот зазор не поместится ещё один такой же «сдутый» куб, тогда мы получим {4,3,5} — разбиение 3-мерного пространства Лобачевского на кубы. Когда мы сдували кубы, то строго говоря, мы их поместили в пространство Лобачевского.
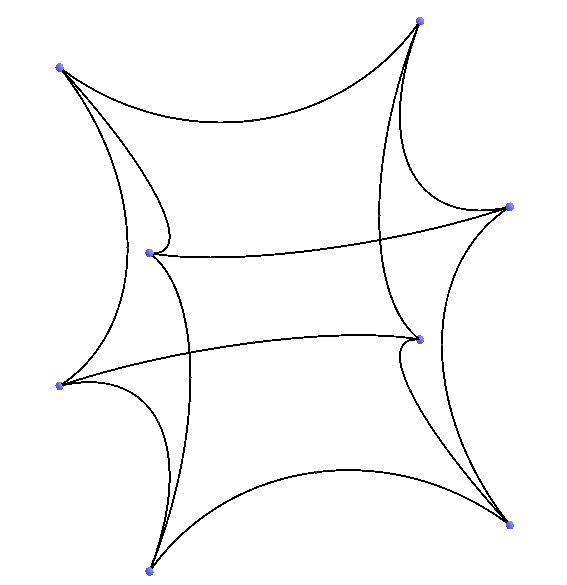
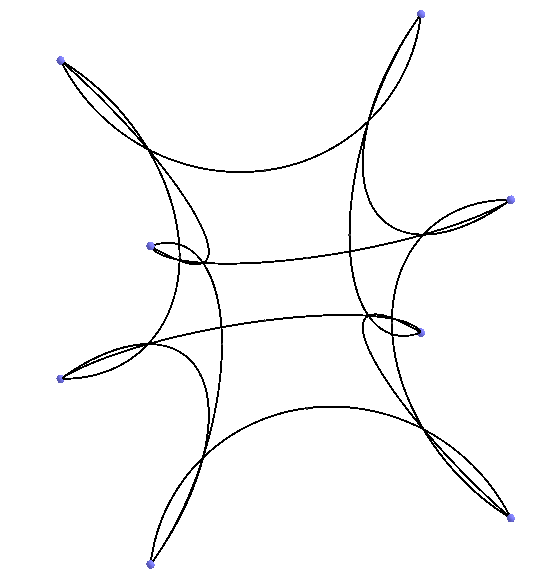Сдутые кубы мы уже видели выше на одном из видео (рисунок слева). Вот так, путём сдувания, получаются разбиения трёхмерного пространства Лобачевского, на правильные многогранники. Только надо быть осторожными, нельзя слишком долго сдувать кубы, иначе образуются самопересечения рёбер (рисунок справа). Это на рисунке у нас самопересечения образовались, а в смысле 3-мерного пространства Лобачевского это означает, что вершины куба вышли за абсолют. Так по шесть кубов в ребре обозначается Символом Шлефли {4,3,6} и уже у этого разбиения 3-мерного пространства Лобачевского вершины находятся прямо на абсолюте. У {4,3,7} вершины уже уходят за абсолют, эти Символы Шлефли тоже показывают разбиения 3-мерного пространства Лобачевского, но строго говоря уже не на правильные многогранники, а на нечто другое, здесь уже можно придумать как называть эти объекты и договориться об их названии.Мы поработали с кубами, аналогично получаются разбиения из других трёхмерных правильных многогранников.
{3,3} — тетраэдры, объединяем по три тетраэдра в ребре {3,3,3}, остаётся зазор, надуваем их до склейки граней, получаем разбиение 3-мерной сферы на тетраэдры, сходящихся по 3 штуки в ребре. Это разбиение задаёт правильный многогранник в 4-мерном Евклидовом пространстве {3,3,3}.
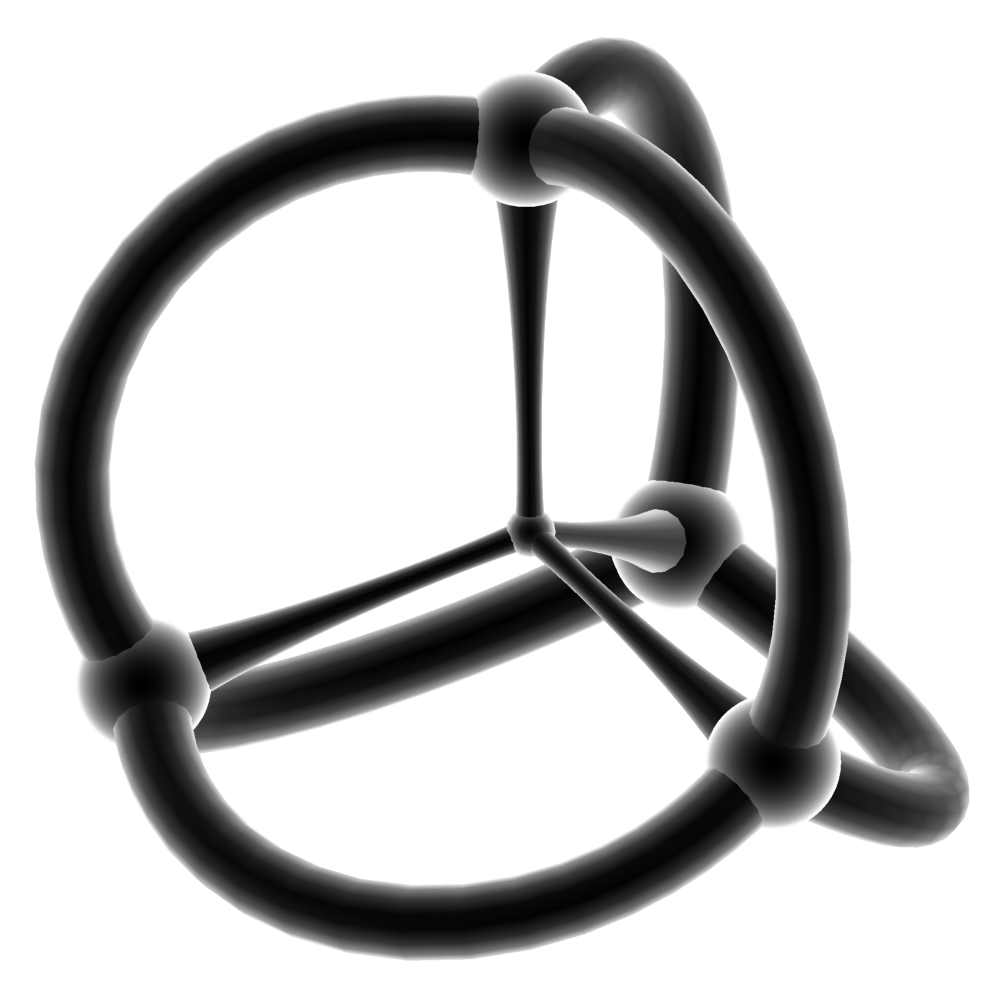
Рис. 22 Разбиение трёхмерной сферы {3,3,3}.
Рис. 23 Четырёхмерный многогранник {3,3,3}
С остальными разбиениями 3-мерной сферы и многогранниками аналогично.
Рис. 24 Разбиение трёхмерной сферы {3,3,4}.
Рис. 25 Четырёхмерный многогранник {3,3,4}
Рис. 26 Разбиение трёхмерной сферы {3,3,5}.
Рис. 27 Четырёхмерный многогранник {3,3,5}
Рис. 28 Разбиение трёхмерной сферы {3,4,3}.
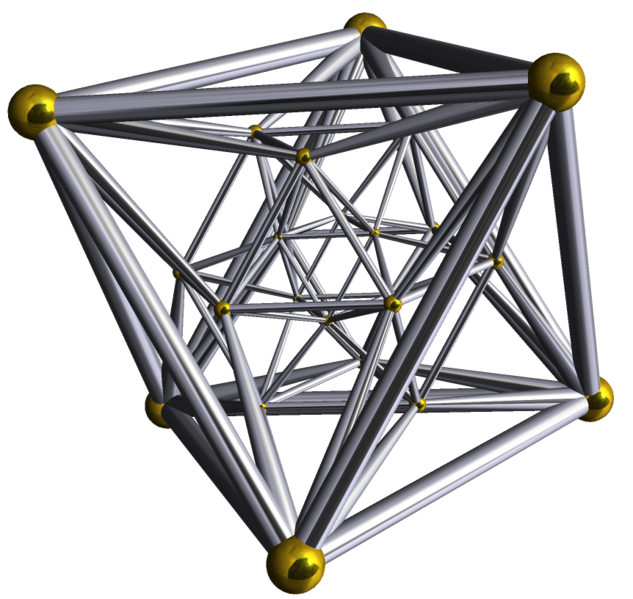
Рис. 29 Четырёхмерный многогранник {3,4,3}
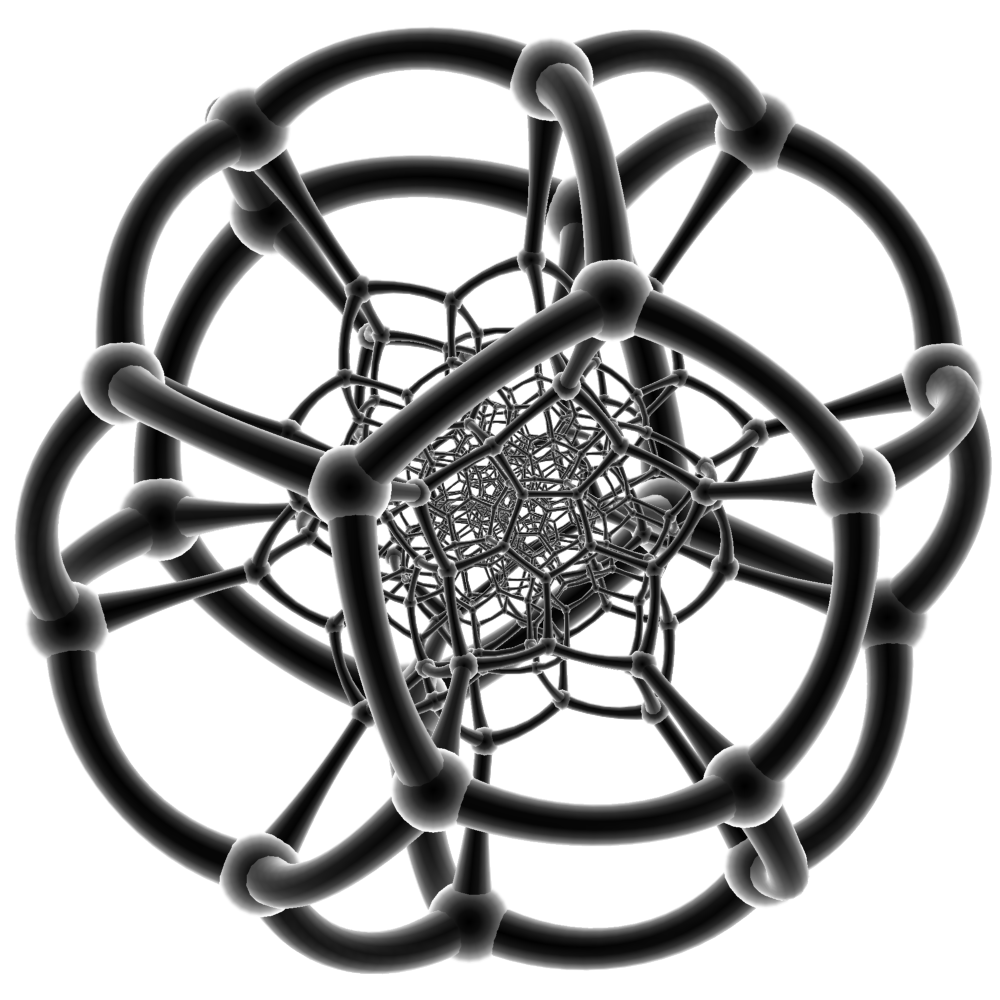
Рис. 30 Разбиение трёхмерной сферы {5,3,3}.
Рис. 31 Четырёхмерный многогранник {5,3,3}
С разбиениями 3-мерного пространства Лобачевского тоже всё аналогично, только многогранники нужно сдувать и не забывать, чтобы вершинки не вылетали за абсолют. Определить где находятся вершинки по Символу Шлефли очень легко, для {p1, p2, p3} рассматриваем Символ {p2, p3}, если {p2, p3} — разбивает плоскость Евклида, т.е. принимает одно из значений {4,4}, {3,6}, {6,3}, то это верный признак, что вершинки {p1, p2, p3} НА абсолюте, например это {3,3,6}, {3,4,4}, {3,6,3} и другие. Если {p2, p3} — разбивает плоскость Лобачевского, то вершинки {p1, p2, p3} ЗА абсолютом, например это {3,3,7}, {3,4,5}, {3,6,4} и другие. Если {p2, p3} — разбивает сферу, но при этом {p1, p2, p3} — не разбивает сферу, значит {p1, p2, p3} — разбивает 3-мерное пространство Лобачевского, эти варианты перечислю все, это: {4,3,5}, {3,5,3}, {5,3,4}, {5,3,5} других таких нет.
Для многогранников и разбиений в остальных размерностях пространств дела обстоят полностью аналогично. Символ Шлефли для пространств высших размерностей будет записываться {p1, p2, p3, p4, … pn}
Научитесь надувать и сдувать шарик и у вас не останется трудностей с пространствами постоянной кривизны.
И в заключение пару слов о свойстве дуальности многогранников. Если Символ Шлефли записать в обратном порядке, то получим тоже правильный многогранник, только дуальный к исходному. Так октаэдр и куб дуальны друг другу, т.е. {3,4} — {4,3}. Тетраэдр самодуален {3,3} — {3,3}. Икосаэдр и додекаэдр дуальны, {3,5} — {5,3}. Это очень важное свойство, которое помогает вычислять размеры рёбер и углы правильных многогранников. При построении всех чертежей, которые я использовал в статье, я пользовался этим свойством очень активно. Также при построении додекаэдра очень важным оказалось свойство, что куб чётко вписывается внутрь додекаэдра, прямо вершины куба попадают на вершины додекаэдра. Это помогло найти координаты 8 вершин додекаэдра, остальные вершины додекаэдра было найти не сложно. Вот такие они, многогранники, очень похожи друг на друга. Дуальность геометрически означает, что вершины одного многогранника упираются в центры плоских граней второго многогранника дуального первому. На примере трёхмерных многогранников эти все свойства показаны на видео.
Можно скачать исходники и поиграться самостоятельно.
Изгибание рёбер куб
Изгибание рёбер октаэдр
Там же найдёте программу для просмотра и редактирования этих чертежей.
Свойство дуальности сохраняется и во всех остальных размерностях пространств, так {3,3,5} дуален {5,3,3} и т.д.
Спасибо, что дочитали «многа букыв» до конца. На связи. Пока.
