Сам себя не потренируешь — никто не потренирует
Однажды мой коллега для кругозора заинтересовался темой построения треугольника Серпинского с помощью «игры в хаос». И познакомил с ней меня. Показал видео. Потом он сказал: «Ты же учишься программировать — попробуй написать программу, в которой это будет реализовано».
Я не специалист в этой области, могу ошибаться в терминах или не очень правильно их интерпретировать и применять.
Про этот треугольник
Треугольник Серпинского — это вот такая штука:
По сути это фрактал. Берётся равносторонний треугольник (пусть он будет ). Середины его сторон соединяются отрезками. Получаются четыре треугольника. Из
удаляется треугольник, находящийся посередине. Остаётся три угловых треугольника
Также поступают и с каждым из них. Получаются девять треугольников
Продолжают до бесконечности — получается треугольник Серпинского.

Игра в хаос
Способ его построения с помощью игры в хаос заключается в следующем (здесь рассказывается с математикой). Берётся равносторонний треугольник (пусть углы будут A, B и C). Внутри произвольным образом выбирается начальная точка. Бросается игральная кость. Будем говорить для определённости, что выпадение того или иного числа на кости соответствует следующим результатам:
»1» или »4» — это А;
»2» или »5» — это В;
»3» или »6» — это С.
Разумеется, это условно. Важно лишь, чтобы А, В и С имели одинаковую вероятность выпадения.
Допустим, в результате первого броска выпала А. Тогда вершина А мысленно соединяется с начальной точкой отрезком, а на середине этого отрезка ставится точка. Пусть теперь она будет начальной.
Следующий бросок игральной кости. Допустим выпала С. Значит теперь уже мысленным отрезком соединяем новую начальную точку и вершину С, и, опять же, отмечаем середину этого отрезка точкой и перетаскиваем туда нашу начальную точку. И так далее.
После достаточно большого количества повторений из точек получим изображение того самого треугольника Серпинского. В теории, по крайней мере.
Не особо важные спойлеры.
Выяснилось, что
Ты же учишься программировать…
Я не работаю в сфере IT. Учусь программировать на C++ по учебникам. Но скорее просто для того, чтобы заставлять свою голову работать. Полагаю, сейчас, чтобы податься в IT нужно учиться владеть каким-то более высокоуровневым инструментом или чему-то более прикладному. Зерокодингу, например. Так что для меня это что-то вроде хобби или аналога разгадывания сканвордов.
Мой коллега знает об этом и не видит ничего плохого в том, чтобы подкинуть мне практику. На тот момент всё, что я умел, это выводить что-то в консоли. Я взял задачку себе на заметку. Со временем я пришёл к тому, как реализовать это в виде приложения для Windows. В итоге я написал эту программу с использованием WinAPI. В этом мне помогла книга Юрия Щупак «Win32 API. Эффективная разработка приложений», 2007. Это было довольно занятно.
Интерфейс приложения
Есть несколько рабочих версий программы. Последняя выглядит так:

На зелёную рамку не обращайте внимания. Я уже не помню точно, но, скорее всего, так я отрабатывал использование геометрических примитивов и разные цвета.
Ну так вот, всё просто. Пожалуй, прежде пройдусь по control«ам интерфейса.
Как видите, тут есть меню. Правда, не очень функциональное. «Выход» реально это и делает. А вот всё остальное просто выводит информационное диалоговое окно, у которого надо нажать «ОК» или закрыть:
А вот пункту «Параметры» в конструкторе меню его свойству «Всплывающее окно» присвоен «false», поэтому он не является раскрывающимся подменю следующего уровня:
Почему-то мне кажется, будто от горячих клавиш там лишь одно название. Пожалуй, не буду возвращаться и проверять это. Но знайте, что тему эту я прошёл и при желании могу реализовать. По крайней мере, знаю, где про это написано.
Так я осваивал создание меню.
Поле с контролами слева — это Modeless Dialog Box, или же диалоговое окно, которое не забирает себе монопольно фокус приложения, а вполне себе сосуществует с ним.
Кнопка «Do it!» выполняет установленное количество итераций с бросками игральной кости и рисованием точек внутри треугольника. Но делает она это только, если на рабочем поле имеются четыре точки — три вершины и начальная точка. А иначе:
Итерация — это:
генерация рандомного числа от 1 до 6;
на основании этого расчёт положения следующей точки;
её рисование.
Если для кого-то это важно, то перед rand () идёт srand (time (NULL)).
«Refresh» это «Clear».
Следующий элемент интерфейса — Edit Control для ввода количества выполняемых за одно нажатие «Do it!» итераций:
При запуске программы эта величина по умолчанию равна единице.
Почему не больше 100000? В общем-то, ничего страшного не произойдёт. Просто никакой речи о многопоточности на тот момент не было. Плюс, в какой-то момент я использовал вектор в качестве хранилища информации обо всех точках. Поэтому при генерации большого количества точек поток замыкается в себе до тех пор, пока все точки не нарисуются.
Уже много позже я научился обходиться без кнопки для ввода нового значения. Реализовал я это уже в другой тренировочной программе.
сколько итераций при нажатии «Do it!» происходит;
текущий радиус точки;
количество уже нарисованных точек;
какой n-угольник будет вначале (опять же, про это позже).
Работа приложения
Вначале я ввожу количество точек, рисуемых одним нажатием «Do it!», ну скажем, 10000. Затем делается три клика на рабочем поле, появляются вершины треугольника, которые автоматически последовательно соединяются линиями. Ещё один клик — создаёт начальную точку. Дальше нажимаем «Do it!». И Вуа ля!

Если ещё несколько раз понажимать, то линии станут чётче:
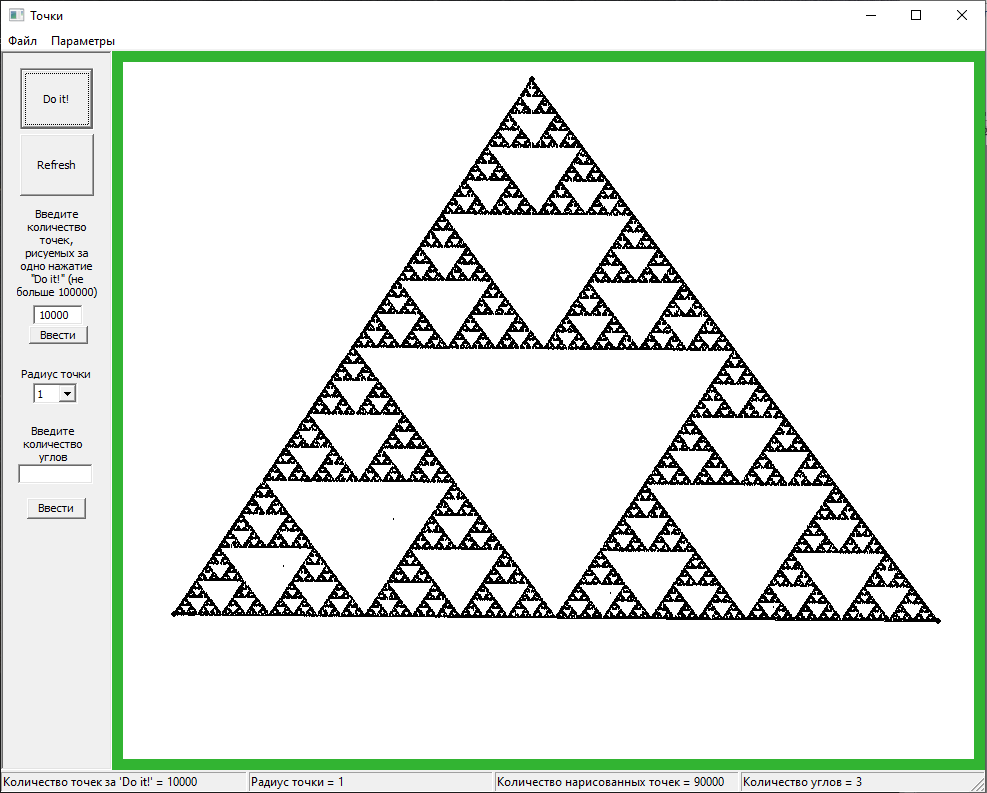
Когда я впервые в рабочем виде реализовал эту программу, я, честно говоря, был в шоке. Шеогоратова математика!

Вот ещё несколько реализаций:
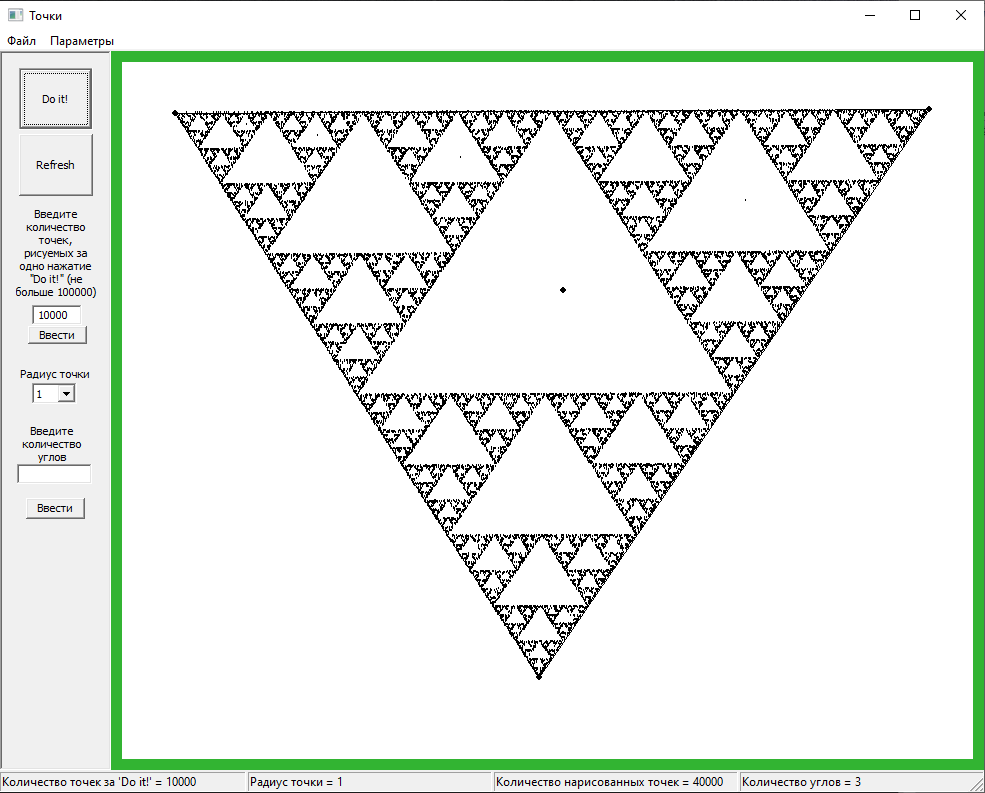
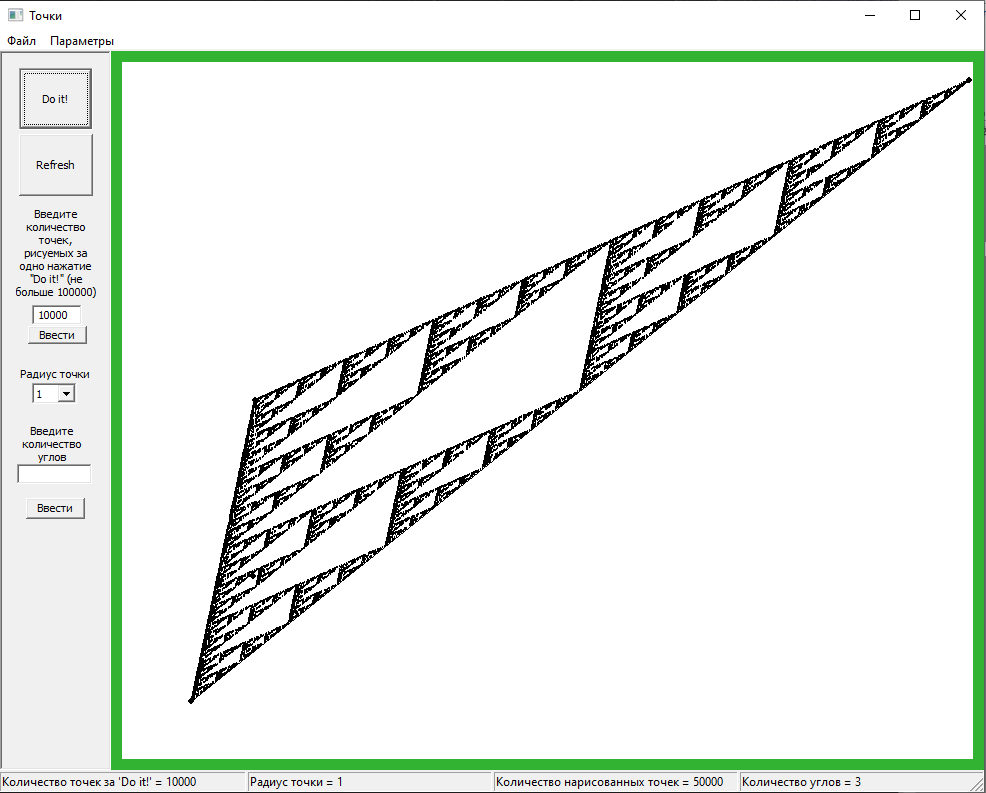
Как я ранее писал, действительно, треугольник может быть каким-угодно. А ещё, если поставить начальную точку вне треугольника, то это ни на что не повлияет. Оно и логично! Потому что рано или поздно точка попадёт внутрь треугольника, а там уже по накатанной.
Итак, задача решена!
Про количество углов фигуры
Мне стало интересно, что же будет с n-угольником, где n > 3. Я добавил кое-какие изменения в код программы и реализовал задачу. В начальных версиях этого функционала не было.
Собственно, вводим в соответствующий Edit Control количество углов и смотрим. Как мне показалось, разные угольники ведут себя по-разному.
Для очень неправильного четырёхугольника выходит что-то такое:
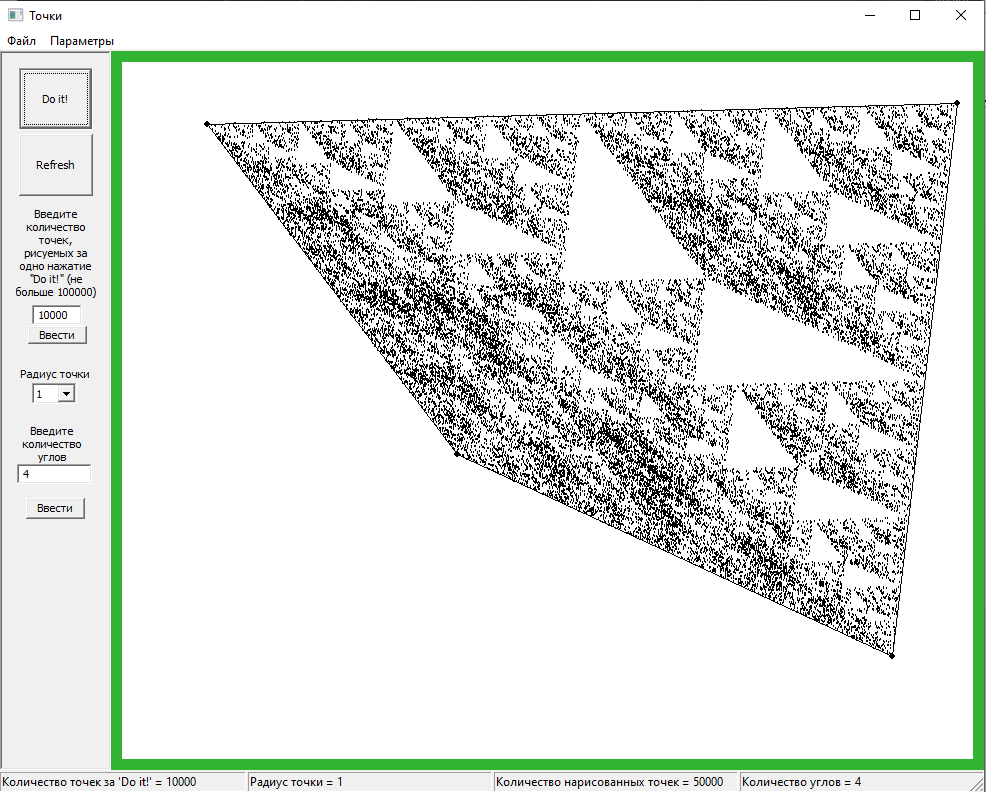
Чем «параллельнее» несмежные стороны, тем однороднее получается распределение точек:
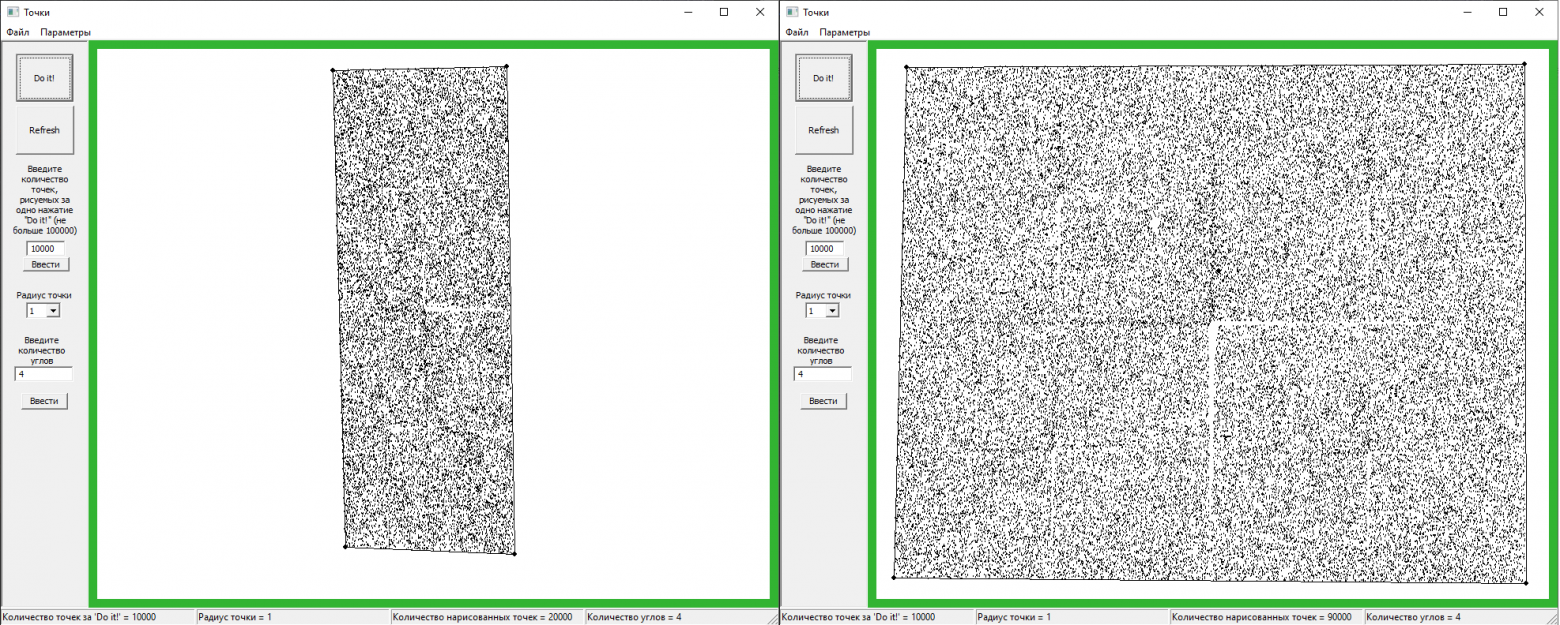
В центре можно разглядеть степень «ошибки параллельности».
И ещё кое-что. Если две вершины поставить достаточно близко друг к другу, получается эффект треугольника, но в той стороне, где находятся эти две близкие друг к другу вершины, плотность точек больше. Довольно логично.
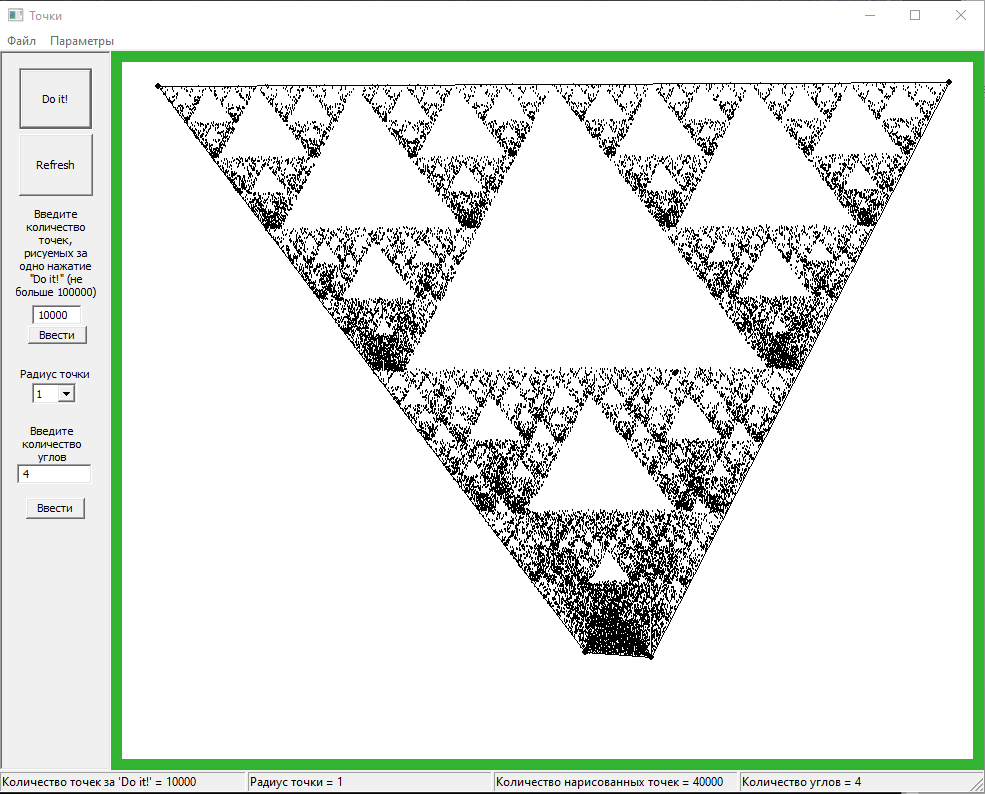
С пентагоном и гексагоном тоже, вроде как, можно выделить какие-то закономерности:
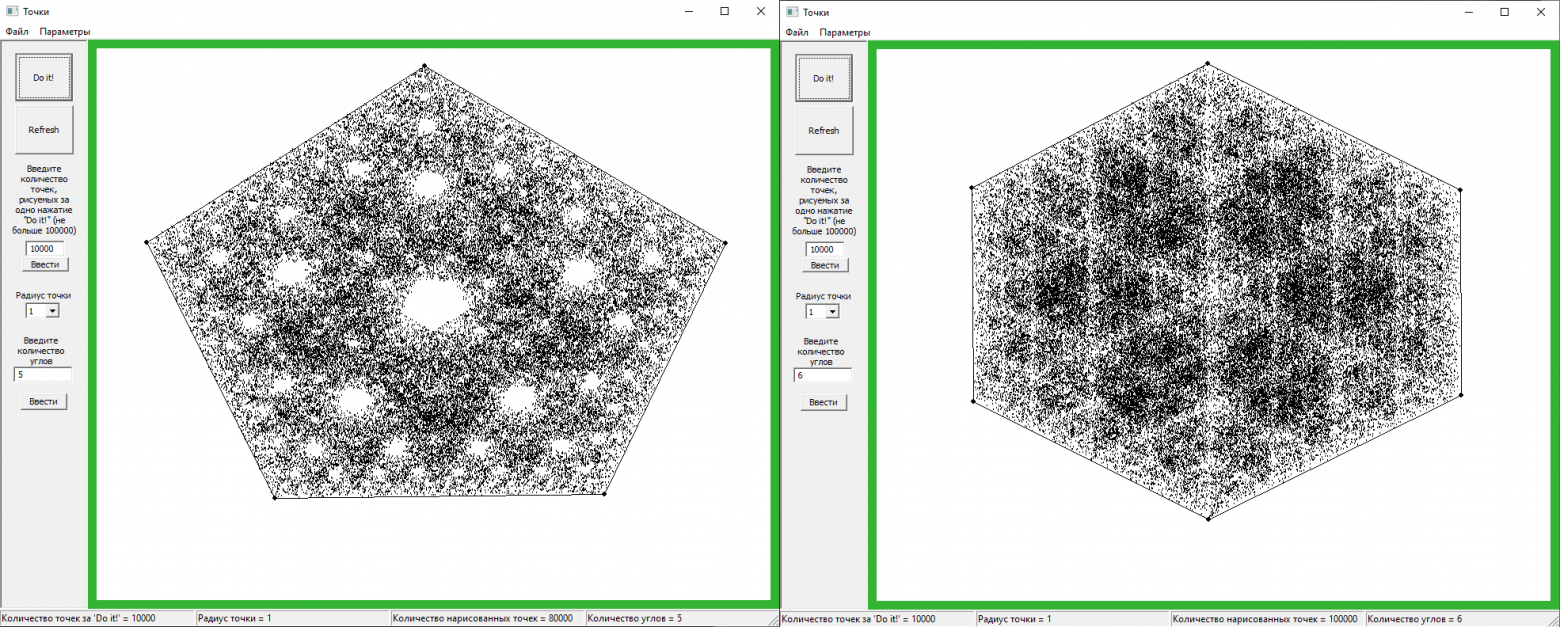
А эффект треугольника на них тоже распространяется:
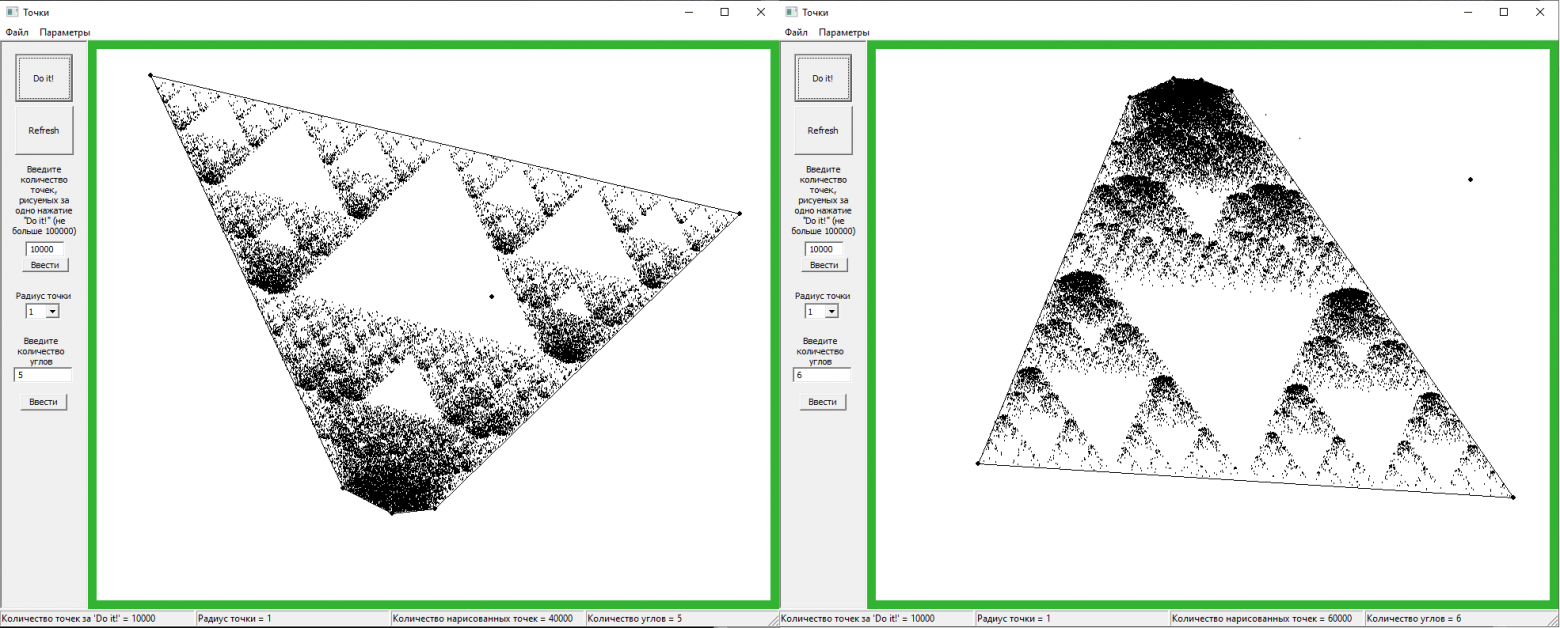
Наращивая дальше количество углов ничего особо интересного я уже не нашёл. Думал, может с октагоном будет что-то интересное, но нет.
Надеюсь, кому-то было интересно. Всем добра!
