Рубрика «Читаем статьи за вас». Февраль — Март 201805.04.2018 14:48

Привет, Хабр! Продолжаем публиковать рецензии на научные статьи от членов сообщества Open Data Science из канала #article_essense. Хотите получать их раньше всех — вступайте в сообщество!

Статьи на сегодня:

1. Learning Semantic Segmentation with Diverse Supervision (University of Manitoba, Shanghai University, 2018)
2. TVAE: Triplet-Based Variational Autoencoder using Metric Learning (Stanford University, 2018)
3. Neural-Symbolic Learning and Reasoning: A Survey and Interpretation
4. Overcoming catastrophic forgetting in neural networks (DeepMind, Imperial College London, 2016)
5. Deep Image Harmonization (University of California, Adobe, 2017)
6. Accelerated Gradient Boosting (Sorbonne Université, Univ Rennes, 2018)

1. Learning Semantic Segmentation with Diverse Supervision

Авторы статьи: Linwei Ye, Zhi Liu, Yang Wang (University of Manitoba, Shanghai University, 2018)
→ Оригинал статьи
Автор обзора: Егор Панфилов (в слэке egor.panfilov)

В данной статье авторами предлагается архитектура для обучения CNN в задаче семантической сегментации, которая позволяет использовать для обучения данные с различными типами разметки (попиксельные маски, bounding box’ы, лейблы для всего изображения).

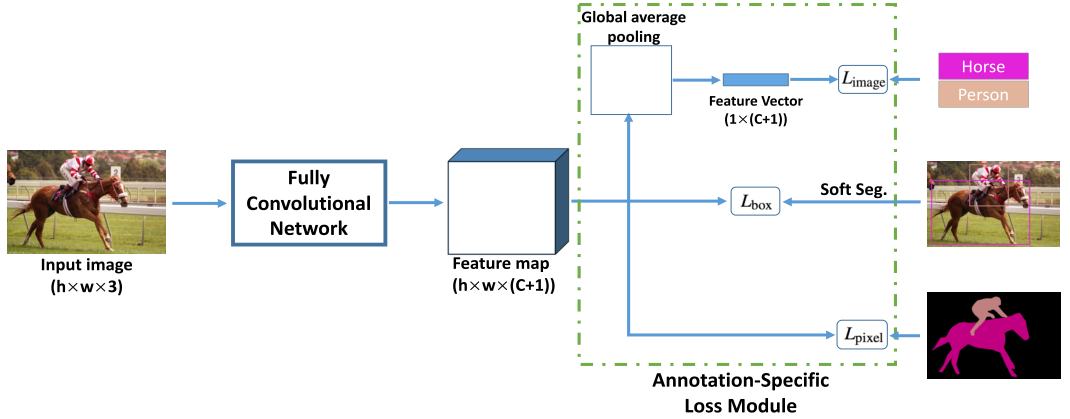
Архитектура представляет собой FCN, принимающий тензор (hw3) на вход, и выдающий тензор (hw(C+1)), т.е. с такими же пространственными размерностями, как и исходное изображение. Выходная карта признаков после этого используется в трёх головах для расчёта лосса: (1) L_image (global average pooling → multi-category BCE loss), (2) L_bbox, (3) L_pixel (усреднённая попиксельная BCE).

L_bbox — одна из самый интересных частей статьи. Проблема здесь в том, как превратить bbox для какого-либо объекта в скаляр лосса. Подход авторов состоит в генерации на основе bbox’а приближенной маски объекта (испробованы Grabcut, MCG, простая заливка bbox’а, и UCM (ultrametric contour map)). Лучше всего заработал UCM, точнее его версия, где при перекрытии нескольких bbox’ов пиксель учитывается для каждого класса (soft.segm.). Вариант, где он назначается одному классу (hard.segm.) показал себя чуть хуже. Генерация маски по UCM работает так: (а) выделяем по UCM контуры, (б) нормируем по интенсивности, (в) задаём 3 значения трешхолда (¼, 2/4, ¾), (г) начинаем заливать концентрические контуры пока не выйдем по площади за какое-то количество %. Остаткам частных масок по этим трешхолдам назначаем лэйбл uncertain — их игнорируем при расчёте лосса. Имея предсказание сети и созданную опорную маску, считаем лосс.

По экспериментам: авторы обучали FCN и DeepLab на PASCAL VOC 2012, используя различными типы разметки и в раличных пропорциях (маски: bbox: лейблы — от 1:1:1 до 1:5:10). Результаты показывают, что bbox’ы добрасывают прилично, но при совсем кислой разметке (когда попиксельных масок очень мало) помогают и image-level лэйблы.

2. TVAE: Triplet-Based Variational Autoencoder using Metric Learning

Авторы статьи: Haque Ishfaq, Assaf Hoogi, Daniel Rubin (Stanford University, 2018)
→ Оригинал статьи
Автор обзора: Егор Панфилов (в слэке egor.panfilov)

В статье свежая кровь из Стенфорда старается сделать контрибьюшен в область Deep Metric Learning. Не отвечая на вопрос зачем, и какую, собственно, проблему они пытаются решить, авторы предлагают взять VAE для картинок, вытащить из боттлнека вектор mean’ов (не обращая внимания на дисперсии), и дополнительно накрутить поверх него триплет лосс. Таким образом, сеть обучают на смешанном лоссе: L_tv_ae = L_reconstruction + L_KL + L_triplet.
Обучают на MNIST с размерностью эмбеддингов в 20 непонятную сеть с непонятно какими параметрами непонятное количество времени. Оценивают тоже чёрт знает как — путём подсчёта после обучения процента триплетов, на которых триплет лосс нулевой. Показатель по данной «метрике качества» улучшается, что, вообще говоря, ожидаемо, так как его обратную версию добавили к функции потерь и, соответственно, старались минимизировать. В качестве заключительной ноты — t-SNE эмбеддингов на двух подходах (VAE и VAE+triplet) с неизвестной perplexity. Кластеры классов (кажется) выглядят более компактными, также значительно меньше случаев, когда один класс представлен несколькими кластерами.

3. Neural-Symbolic Learning and Reasoning: A Survey and Interpretation

Авторы статьи: Besold, Garcez, Bader, Bowman, Domingos, Hitzler, Kuehnberger, Lamb, Lowd, Lima, de Penning, Pinkas, Poon, Zaverucha
→ Оригинал статьи
Автор обзора: Евгений Блохин (в слэке @eb)

Этот обзор описывает нейросимвольные вычисления как попытку объединить два подхода к AI: символизм и коннекционизм. В нём 58 страниц, он очень многословный, привожу наикратчайший конспект в двух частях. Часть 1. (edited)
С одной стороны, логика (символизм) есть «исчисление информатики», и на протяжении десятилетий логика «правила бал» и активно развивалась (cм. GOFAI). Сегодня существует темпоральная, немонотонная, дескрипционная и другие типы логики. Управление знанием есть детерминированный процесс. С другой стороны, машинное обучение (коннекционизм) имеет статистическую природу. В очень общем смысле, это два эквивалентных подхода: они вычислимы и могут быть представлены конечными автоматами. Нейросимвольные сети не являются новым подходом. В общем, логические рассуждения (reasoning) широкого спектра выразительности могут выполняться нейросимвольными сетями, и ключевой момент здесь модульность.

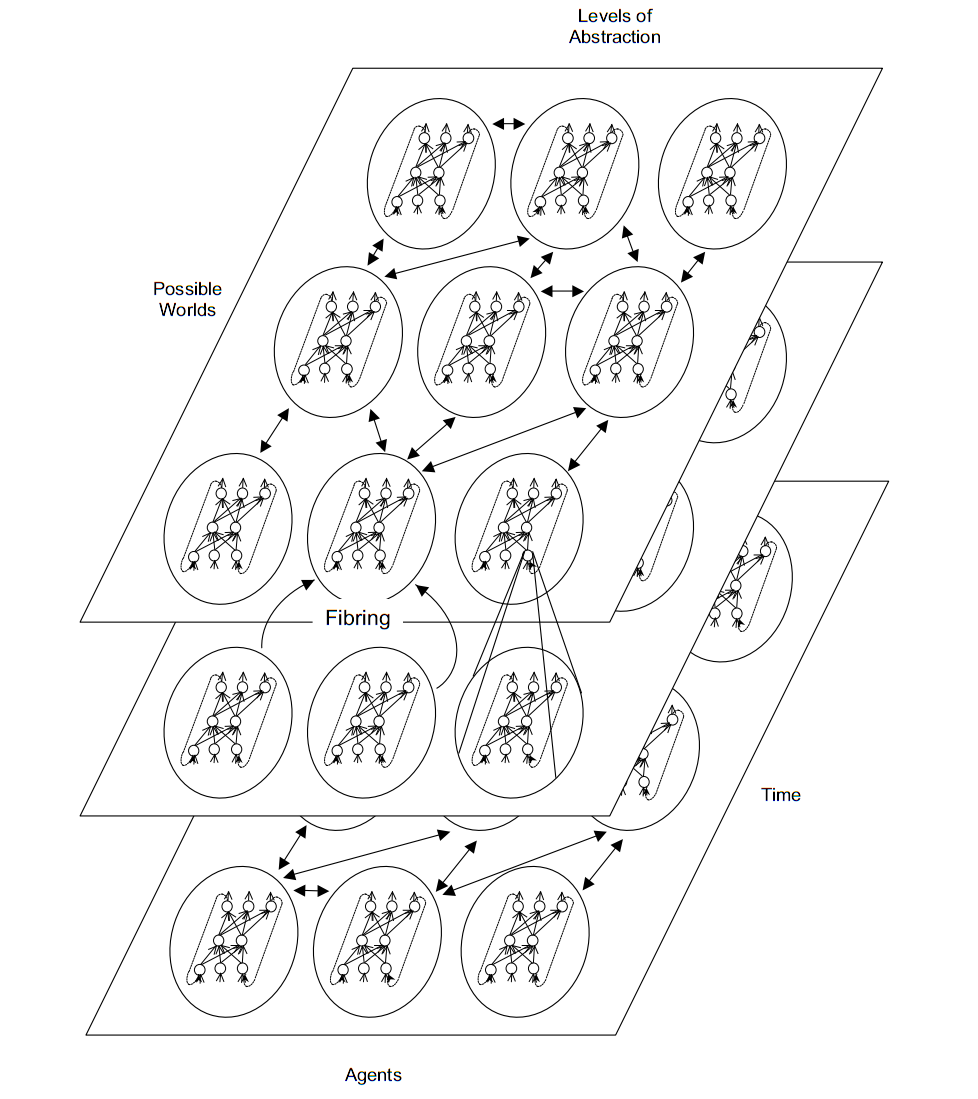
Например, говоря про многоуважаемого Хинтона и его глубокое обучение, мы можем представить себе нейросимвольную сеть как фибринг (fibring, расслоение), когда подсети, отвечающие за символьное знание, формируются друг в друге рекурсивно. Представим себе переменные X, Y и Z и две подсети, отвечающие за концепции P (X, Y) и Q (Z). Тогда мета-сеть в фибринге отобразит P и Q на новую концепцию R (X, Y, Z) так, что P (X, Y) ^ Q (Z) → R (X, Y, Z). Хотя практическая имплементация очень сложна. Когнитивная модель должна обрабатывать комплексные связи в наблюдаемых данных (напр. тактические манёвры, безопасное вождение). К сожалению, человек-эксперт зачастую делает это недетерминированно и субъективно (например, основываясь на стрессе или усталости), и не вполне ясно, как передать модели этот опыт.

Другой пример: архитектура NSCA (Neural Symbolic Cognitive Agent), основанная на рекуррентной темпоральной ограниченной машине Больцмана (RBM) от Суцкевера, Хинтона и Тейлора (2009). Двухслойная сеть RBM получает на вход некие знания в виде темпоральной логики, изменяя свои веса, a расчёт выходных величин по весам в ответ на входные вектора представляет собой вероятностное рассуждение. Таким образом, правила темпоральной логики заданы весами RBM. Архитектура NSCA была использована в симуляторах вождения, в проекте DARPA Mind’s Eye и системах Visual Intelligence. Также в 2014 она была задействована в автомобильных системах снижения выбросов CO2. Сейчас её интегрируют с глубокими Больцмановскими машинами от Хинтона и Салахутдинова, хотя намекается, что у NSCA есть ещё много нерешённых проблем.
Нейросимвольные системы берут начало в когнитивистике и нейронауках. Первая теория человеческого мышления была сформулирована ещё Johnson и Laird в 1983. До сих пор центральная проблема — это механизм нейронного связывания (binding problem), т.е. как именно изолированные образы компонуются друг с другом. Например, теория конъюнктивных кодов (conjunctive codes) для нейронного связывания ближе всего к существующим искусственным нейросетям (ИНС). По этой теории, для нейронов в мозгу нет единого связывающего ресурса (комбинаторный взрыв), но существуют хорошо масштабирующиеся распределённые представления, причём, случайно возникающие и эффективно дискриминируемые. Однако нейронауки в основном отвергают современные ИНС для объяснения мышления, хотя и признают их заслуги. Так, начиная с 1988 Fodor и Pylyshyn утверждают, что мышление симолично по своей природе, приводя занимательную аналогию с software и hardware. Функциональная сложность находится в software, символичном по своей природе, и любой алгоритм определяется именно software, а не его представлением в hardware. Далее, современные эксперименты показывают, что человек тяготеет к использованию правил для решения когнитивных задач, и эти правила индивидуальны и коррелируют с IQ. Кроме того, существует центральная исполнительная функция, ответственная за планирование и локализированная в лобной доле. Далее, среди психолингвистов до сих пор ведутся дебаты о том, основана ли языковая морфология на правилах или на ассоциациях. Наконец, коннекционизм не отражает репрезентативную композиционность, присущую многим когнитивным способностям (Иван в предложении «Иван любит Машу» != Иван в предложении «Маша любит Ивана»). В концепции современных ИНС вышеупомянутые аспекты неразрешимы.

Логические рассуждения в современных ИНС представляются следующим образом (см. работы Pinkas и Lima, 1991–2013). Cкажем, что наша задача есть вывод по базе знаний в логике первого порядка, и возьмём ИНС с симметричной матрицей весов (например, RBM). Наша база знаний будет предствлена весами или активацией каких-либо нейронов. Тогда ИНС проводит градиентный спуск для функции энергии, глобальный минимум которой есть вывод в нашей цепочке рассуждений.

Во второй части примеры рассуждений и логических операций первого порядка в ИНС, логические сети Маркова, примеры других подходов с применением LSTM, сложности и прогнозы на будущее.

4. Overcoming catastrophic forgetting in neural networks

Авторы статьи: James Kirkpatrick, et. al. (DeepMind, Imperial College London, 2016)
→ Оригинал статьи
Автор обзора: Яна Середа (в слэке @yane123)

Сделали предположение о том, что не все параметры сети одинаково важны для производительнсти на выученной задаче А. Решили модифицировать алгоритм обучения так, чтобы он выявил «важные» для уже выученных задач веса и защитил бы их от сильного изменения — пропорционально степени их важности для прошлых выученных задач.

Это было достигнуто прибавлением штрафа к функции потерь. Наказание за изменение параметра (веса или биаса) выбрано пропорционально квадрату изменения. Коэффициентом же пропорциональности (то бишь показателем важности параметра для задачи А) работает информация Фишера, посчитаная для этого параметра и датасета задачи А. Для расчета матрицы Фишера достаточно первых производных.

Если после задач А и В начать учить сеть задаче С, то функция потерь, соотвественно, будет уже из трех слагаемых (за порчу А, за порчу В и за качество решения С).

Также предложили способ померить степень переиспользования сетью одних и тех же весов для решения разных задач — «перекрытие Фишера».

Эксперименты: на синтетике, мнисте и атари

5. Deep Image Harmonization

Авторы статьи: Yi-Hsuan Tsai, Xiaohui Shen, Zhe Lin, Kalyan Sunkavalli, Xin Lu, Ming-Hsuan Yang (University of California, Adobe, 2017)
→ Оригинал статьи
Автор обзора: Арсений Кравченко (в слэке @arsenyinfo)

Если вырезать объект с одной картинки и тупо вставить на другую, несложно догадаться, что дело нечисто — в глаза бросаются различия в освещенности, тенях и т.п. Чтобы замаскировать свою деятельность, мастера фотошопа крутят какие-то кривые, но DL пацаны имеют альтернативное решение.

Давайте обучим end-to-end сеть, которая будет превращать плохо отфотошопленные фотографии в почти настоящие. Проблема с данными: классических пар X, Y для supervised learning здесь нет. Но можно сгенерить такие данные: возьмем картинку из датасета вроде COCO, выберем на ней объект по маске и «испортим» его — перенесем на него цветовые характеристики (например, при помощи histogram matching; впрочем, авторы использовали и много более продвинутых методик). Т.к. COCO недостаточно разнообразен, докинем аналогичным образом искаженных картинок с фликра и отфильтруем (привет, #proj_kaggle_camera!) слишком отвратительные при помощи aesthetics prediction model.

Теперь можно и учить сеть енкодер-декодер архитектуры : unet: превращать искаженные картинки + маски искажения в оригинальные, используя обычный L2 лосс. Чтобы дополнительно повысить качество, займемся multi-task learning: добавим вторую ветку декодера, которая будет отвечать за семантическую сегментацию, а в лосс, соответственно, добавим кросс-энтропию. Итоговая архитектура выглядит так

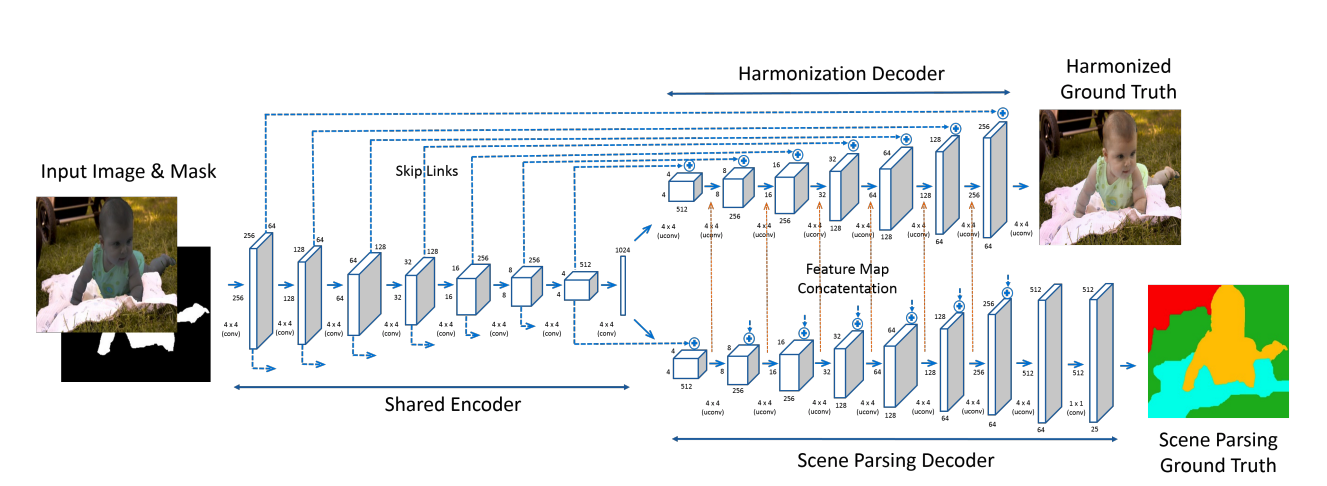
Картинки выглядят реально круто.

Авторы выложили модель и веса на Caffe, но есть и фатальный недостаток — лично я поднять модель пока не смог (кажется, что нужна какая-то фиксированная версия caffe, а вот какая — непонятно).

6. Accelerated Gradient Boosting

Авторы статьи: Gérard Biau, Benoît Cadre, Laurent Rouvìère (Sorbonne Université, Univ Rennes, 2018)
→ Оригинал статьи
Автор обзора: Артем Соболев (в слэке asobolev)

В теории оптимизации известно, что градиентный спуск — довольно медленная процедура. Есть т.н. метод Ньютона, корректирующий направление изменения параметров с помощью матрицы Гессе, но он вычислительно сложнее и требует дополнительных вычислений. Из методов первого порядка, т.е. пользующихся только градиентом и значением функции, оптимальным (для некоторого класса задач) по скорости сходимости является быстрый градиентный метод Нестерова

В данной статье предлагается вставить этот метод оптимизации в градиентный бустинг. Соображеная простые: метод сходится быстрее, значит и такой быстрый градиентный бустинг должен иметь лучшее качество при меньшем количестве ансамблируемых моделей.

Авторы провели несколько экспериментов, сравнившись с обычным градиентным бустингом. Данные использовались странные: несколько синтетических датасетов да пяток оных их UCI репозитория. И правда, авторы показывают (рис. 3), что быстрый градиентный бустинг обучается гораздо быстрее обычного, правда, показывают они это на синтетических данных. В общем же, по результатам своих экспериментов авторы утверждают, что метод работает не хуже, менее чувствителен к learning rate’у и использует меньше моделей в ансамбле.

© Habrahabr.ru