Рогатая сфера Александера — дикая конструкция, которая стала одним из символов топологии
Сегодня я хочу поговорить с Вами о красивейшей из наук — топологии. Начнем мы с очень тривиального рассуждения (за простотой формулировки которого кроется целая бездна), а закончим построением и изучением удивительного объекта — рогатой сферы Александера. Итак, поехали!
Теорема Жордана
Здесь покажу только самую простую формулировку теоремы:
Из рисунка понятно, что если есть замкнутая кривая, которая не имеет самопересечений, то она делит плоскость на две области, и для любых двух точек в одной из областей существует кусочно-ломаная линия, которая их соединяет, не пересекая замкнутую кривую. Соединить же такой линией две точки из разных областей не получится.
Более общее утверждение, получившее название теоремы Шенфлиса гласит, что две области, на которые делит плоскость замкнутая кривая, устроены одинаковым образом.
Одинаковость областей
Здесь необходим некоторый экскурс в топологию. Об «идентичности» двух топологических объектов можно говорить тогда, когда каждое из них может быть получено из другого посредством гомеоморфизма — непрерывного обратимого взаимнооднозначного преобразования. Например, рассмотрим на плоскости несколько треугольников:

Все они гомеоморфны, т.е. топологически эквивалентны: из каждого этого треугольника можно получить другой, растягивая или сжимая стороны. Очевидно также, что любая замкнутая фигура без самопересечений, имеющая большее количество углов, или вообще не имеющая оных (например, окружность), может быть получена путем непрерывных обратимых преобразований из треугольников на рисунке выше.

Расстояния, углы нас не интересуют. Кстати, подобие — это всего лишь частный случай гомеоморфизма.
Одна из главных задач топологии состоит в классификации гомеоморфных объектов. Где-то это можно сделать просто, как на рисунке выше: явным образом предъявить последовательность действий, не нарушающих правил игры.
Топологические и гомотопические эквиваленты
Однако в большинстве случаев непосредственное построение гомеоморфизма затруднено, особенно когда речь идёт о пространствах высших измерений. Поэтому топологи разработали т.н. топологические инварианты — некоторые характеристики объектов, которые не меняются при гомеоморфизмах. Характеристика пространства, которая сохраняется при гомеоморфизме. Иначе говоря, доказать, что объекты (пространства) гомеоморфны — значит предъявить некоторую величину (инвариант), для них одинаковую. Самым наглядным топологическим инвариантом является связность.

Связное пространство не может быть представлено как объединение двух или более непересекающихся непустых открытых подмножеств. Множество А — связно, B — не связно Связность — это обобщение понятия линейной связности. В линейно связном пространстве любые две точки можно соединить непрерывной кривой

Линейно связное пространство называется односвязным, если всякая петля на нём стягивается в точку. Не вдаваясь в строгие формулировки, покажу, что это значит на рисунке:

Любая петля внутри кривой С стягивается в одну точку, а во внешней части есть петля, которая не стягивается (если «опоясать» область С)
Односвязность — это уже не топологический инвариант, а более слабый, т.н. гомотопический. Если пространства X и Y гомеоморфны, то они гомотопически эквивалентны; обратное в общем случае неверно.
Например, окружность гомотопически эквивалентна бублику (полноторию), но не гомеоморфна ему

Именно гомотопическая эквивалентность имеется ввиду под формулировкой «одинаково устроены».
Так вот, теорема Шенфлиса на плоскости утверждает, что две области, на которые делит плоскость любая замкнутая кривая, устроены таким же образом, независимо от формы кривой.
В пространстве же внешность каждой замкнутой поверхности (фактически сферы) не имеет не стягиваемых петель (ведь если надеть петлю на сферу, то благодаря третьему измерению, её легко получится снять). Казалось бы, это верно для любой сферы…однако с доказательством хотя бы для трех измерений сразу возникли проблемы. Что-то подсказывало математикам, что обобщение теоремы не верно.
Джеймс Александер и его «дикая» сфера
Джеймс Александер — американский математик, известный вкладом в топологию и дифференциальную геометрию — в 1924 году предложил контрпример к гипотезе Шенфлиса.

Кстати, Джеймс был женат на русской Наталье Левицкой. У них было двое детей.
Пройдем все этапы построения этого контрпримера. Для начала возьмем диск и «вытащим» из него два рога:

Теперь рассмотрим поверхности этих двух дисков и вытащим из них еще парочку рогов, скрестив из «замком»:

Дальнейшие действия будем повторять бесконечно долго. Таким образом, на первом шаге мы получим 2 рога, затем 4, 8 и т.д. Итак, построили.
Теперь разберемся, во-первых, почему эта штука называется «рогатой сферой Александера», а во-вторых, почему она является контрпримером к гипотезе Шенфлиса. Если с «рогатостью» всё понятно (просто эпитет), то термин «сфера» требует пояснения. Ключевым моментом здесь является понимание, что никакие из «рогов» не соприкасаются между собой.
Да, они могут приближаться до расстояния, заведомо меньшее, любой заданной величины, но всё же! Это значит, что мы можем вернуть всё вспять — т.е. наша деформация является гомеоморфизмом (ни склеек, ни разрывов), а значит перед нами особенная, но всё-таки сфера! Раз у нас сфера, то она обладает свойство односвязности:

А что же с внешностью рогатой сферы Александера? Можем ли мы предъявить такую петлю, которая не может быть стянута в точку? Иными словами, сможем ли мы доказать, что внутренность и внешность сферы гомотопически не эквивалентны? Оказывается, легко и просто!

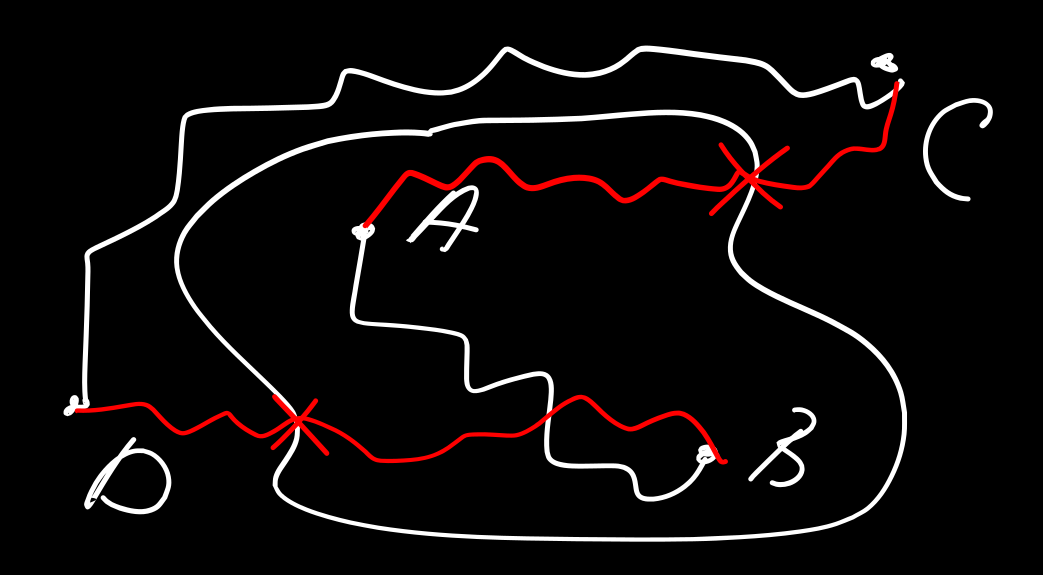
На рисунке выше, показаны примеры трех петель, которые невозможно стянуть. Рано или поздно при попытке снять эту петлю со сферы Александера мы наткнемся на один из её рогов, ведь нам нужно подойти к ним сколь угодно близко, ближе любого наперед заданного значения! А там дебри примерно такие:

Следовательно, внешность сферы Александера и её внутренность устроены иначе, чем внешность и внутренность замкнутой области на плоскости, что опровергает гипотезу Шенфлиса! Спасибо за внимание!
Больше математики в Telegram — «Математика не для всех».
