Решение задачи оптимизации многоступенчатых ракет
Введение
Методы нелинейной оптимизации широко применяются при проектировании машин и механизмов. Указанные методы применяются и в ракетостроении, например, для оптимизации многоступенчатых ракет [1].
Многоступенчатая ракета — это аппарат, в котором части конструкции отделяются во время полета, придавая оставшейся части ракеты дополнительную скорость. Трёхступенчатая ракета схематически показана на рисунке.
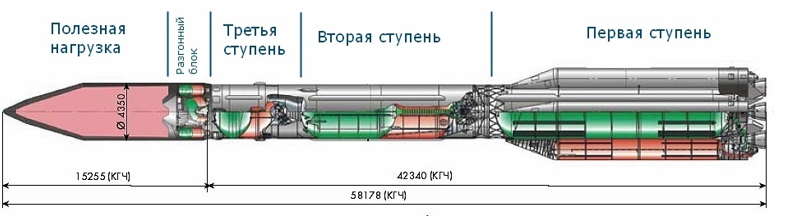
По мере движения ракеты, ступени отделяются до тех пор, пока не останется главная часть ракеты, несущая полезную нагрузку. Задача оптимизации ракеты состоит в таком распределении веса по ступеням, при котором определенная целевая функция достигает максимального либо минимального значения.
Мы рассмотрим две задачи в предположении, что коэффициент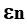 
и скорость реактивной струи Cn постоянны на каждой ступени, однако на разных ступенях могут принимать различные значения. В обеих задачах в качестве целевой функции принят коэффициент полезной нагрузки ракеты G, который необходимо минимизировать.
Характеристики многоступенчатой ракеты можно описать двумя уравнениями. Первое уравнение для коэффициента полезной нагрузки ракеты:
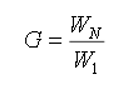
где: W1– полезный вес ракеты ; WN –начальный вес ракеты до отделения ступеней.
Второе уравнение для характеристики полезной нагрузки многоступенчатой ракеты, которое можно записать как выражение для еѐ идеальной конечной скорости (формула К.Э. Циолковского):
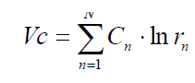
где:
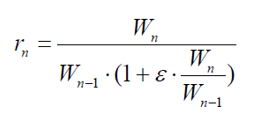
Рассмотрим 4-ступенчатую ракету, движущуюся в отсутствии гравитационного поля с заданными значениями идеальной конечной скорости Vc, начального веса ракеты W4, скорости реактивной струи Cn и коэффициентов Ɛn=Ɛ.
Постановка задач
Первая задача — найти такое распределение веса по ступеням W3, W2, чтобы минимизировать коэффициент полезной нагрузки ракеты G=W4/W1 при заданной скорости Vc.
Вторая задача — найти такое распределение веса по ступеням W3, W2, чтобы максимизировать идеальную конечную скорость Vc при заданном коэффициенте полезной нагрузки ракеты G .
Рассмотрим первую задачу минимизации коэффициента полезной нагрузки при заданной скорости ракеты Vc =1400 м/c и скорости реактивной струи Cn = C =2000 м/с.
В качестве управляющих переменных выбираем распределение веса по ступеням: W3, W2 при заданных значениях начального веса ракеты W4 и коэффициента влияния нагрузки Ɛn=Ɛ=0.3
Представим формулу для вычисления заданной скорости в виде:
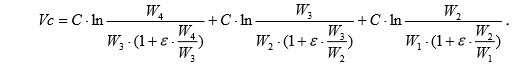
где
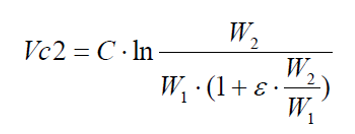
Отсюда следует, что:
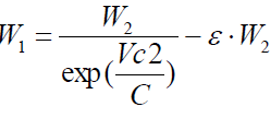
Решение первой задачи на Python
Python является свободно распространяемым языком программирования высокого уровня. До настоящего времени задачи оптимизации решались в лицензионных математических пакетах Maple, Mathcad, Matlab и других.
Несмотря на это, в арсенале средств Python есть замечательные библиотеки numpy и scipy. optimize, использование которых позволяет решать задачи условной и безусловной, а также пользовательской оптимизации. Однако, их использование требует тщательного выбора начальных условий, решателя и функции цели, что мы сейчас и сделаем.
Привожу листинг первой части программы, включая функцию цели:
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import time
C=2000 # скорость реактивной струи
e=0.3# коэффициент нагрузки
VCzad=1400# идеальная конечная скорость ракеты
w4=4000# начальная масса ракеты
def f(a):# вспомогательная функция
return C*np.log(a/(1+e*a))
def VC2(w3,w2):#скорость после отделения первой ступени
return VCzad-f(w4/w3)-f(w3/w2)
def w1(w3,w2):# функция для расчёта массы первой ступени
return (w2/(np.e**(VC2(w3,w2)/C)))-e*w2
start = time.time()# начало отсчета времени работы блока оптимизации
def fun1(x,y):#функция цели с новыми переменными (x=w3, y=w2) в форме удобной для расчетов
return 4000/(-0.3*y+y*np.e**(np.log(x/(0.3*x+y))+np.log(4000/(1200+x))-0.7))Построим контурный график функции цели.
#!/usr/bin/env python
#coding=utf8
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def fun1(x,y):#функция цели
return 4000/(-0.3*y+y*np.e**(np.log(x/(0.3*x+y))+np.log(4000/(1200+x))-0.7))
x= np.linspace(500,5000,10000)
y = np.linspace(500,5000,10000)
z=fun1(x,y)
fig = plt.figure('Контурный график функции цели')
ax= Axes3D(fig)
ax.plot(x,y,z,linewidth=1)
plt.show()Получим:
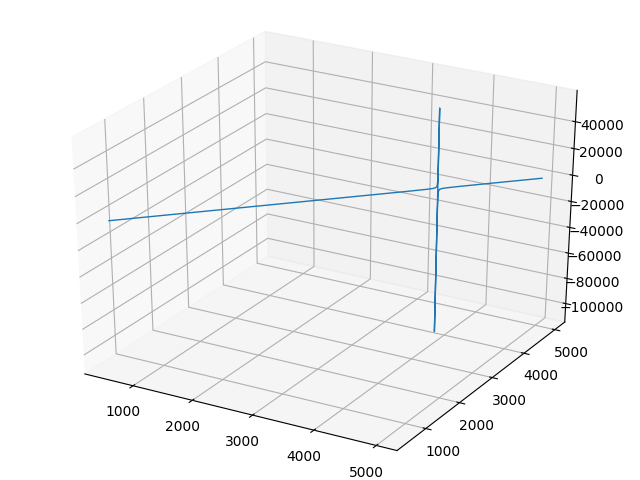
Сложность функции цели состоит в резких изменениях в районе приемлемых значений переменных, поэтому исследуем библиотеку from scipy. optimize import minimize.
Обычно функцию цели записывают в виде [2]: fun = lambda x: (x[0] — 1)**2 + (x[1] — 2.5)**2 (пример). Использование такой записи в решаемой задачи усложнит анализ целевой функции. Для упрощения формы записи целевой функции, применим вспомогательную функцию fun2(x):
def fun2(x):
return fun1(*x)Используем пример из документации [2] для решателя SLSQP:
import numpy as np
from scipy.optimize import minimize
import time
start = time.time()
def fun1(x,y):
return 4000/(-0.3*y+y*np.e**(np.log(x/(0.3*x+y))+np.log(4000/(1200+x))-0.7))
def fun2(x):
return fun1(*x)
x0 =[3000,2000] # начальная точка поиска решения
res = minimize(fun2, x0, method='SLSQP', bounds=None)
stop = time.time()
print ("Время оптимизации :",round(stop-start,3))
print(res)
Получаем следующий результат:
Время оптимизации: 0.0
fun: 8.8345830746128
jac: array ([ 7.71641731e-04, -4.12464142e-05])
message: 'Optimization terminated successfully.'
nfev: 48
nit: 12
njev: 12
status: 0
success: True
x: array ([ 2953.94929027, 1149.31138351])
Варьировать начальной точкой поиска мы не можем, допустим, у нас такое условие, поэтому, для проверки оптимальности решения, перепишем листинг без указания метода:
import numpy as np
from scipy.optimize import minimize
import time
start = time.time()
def fun1(x,y):
return 4000/(-0.3*y+y*np.e**(np.log(x/(0.3*x+y))+np.log(4000/(1200+x))-0.7))
def fun2(x):
return fun1(*x)
x0 =[3000,2000] # начальная точка поиска решения
res = minimize(fun2, x0))
stop = time.time()
print ("Время оптимизации :",round(stop-start,3))
print(res)Получаем следующий результат:
Время оптимизации: 0.0
fun: 8.402280475718243
hess_inv: array ([[ 911166.17713172, 192191.3238931 ],
[ 192191.3238931, 194600.77394409]])
jac: array ([ -1.19209290e-07, 1.31130219e-06])
message: 'Optimization terminated successfully.'
nfev: 152
nit: 28
njev: 38
status: 0
success: True
x: array ([ 1967.29278561, 967.91321904])
Время тоже, но значение функции цели меньше. Поэтому, дальнейшие поиски можно прекратить и представить окончательный листинг в виде:
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import time
C=2000 # скорость реактивной струи
e=0.3# коэффициент нагрузки
VCzad=1400# идеальная конечная скорость ракеты
w4=4000# начальная масса ракеты
def f(a):# вспомогательная функция
return C*np.log(a/(1+e*a))
def VC2(w3,w2):#скорость после отделения первой ступени
return VCzad-f(w4/w3)-f(w3/w2)
def w1(w3,w2):# функция для расчёта массы первой ступени
return (w2/(np.e**(VC2(w3,w2)/C)))-e*w2
start = time.time()# начало отсчёта времени работы блока оптимизации
def fun1(x,y):#функция цели с новыми переменными (x=w3, y=w2) в форме удобной для расчётов
return 4000/(-0.3*y+y*np.e**(np.log(x/(0.3*x+y))+np.log(4000/(1200+x))-0.7))
def fun2(x):
return fun1(*x)
x0 =[3000,2000]
res = minimize(fun2, x0)
stop = time.time()
print ("Время работы оптимизатора :",round(stop-start,3))
print ("Расчётное значение функции цели :",round(res['fun'],3))
w2=round(res['x'][1],3)
w3=round(res['x'][0],3)
w1=round(w1(w3,w2),3)
v1=round(f(w2/w1),3)
v2=round(f(w2/w1)+f(w3/w2),3)
v3=round(f(w2/w1)+f(w3/w2)+f(w4/w3),3)
print("Изменение веса ракеты -:%s;%s;%s;%s "%(w4,w3,w2,w1))
print("Изменение скорости ракеты -:%s;%s;%s;%s "%(0,v1,v2,v3))
VES=[w4,w3,w2,w1]
VC=[0,v1,v2,v3]
plt.title("Распределение веса ракеты при минимальной нагрузке \n для заданной скорости")
plt.plot(VES,VC,'o')
plt.plot(VES,VC,'r')
plt.xlabel("Вес ракеты")
plt.ylabel("Скорость ракеты")
plt.grid(True)
plt.show()
Получаем следующий результат:
Время работы оптимизатора: 0.0
Расчётное значение функции цели: 8.402
Изменение веса ракеты -:4000;1967.293;967.913;476.061
Изменение скорости ракеты -:0;466.785;933.166;1400.001
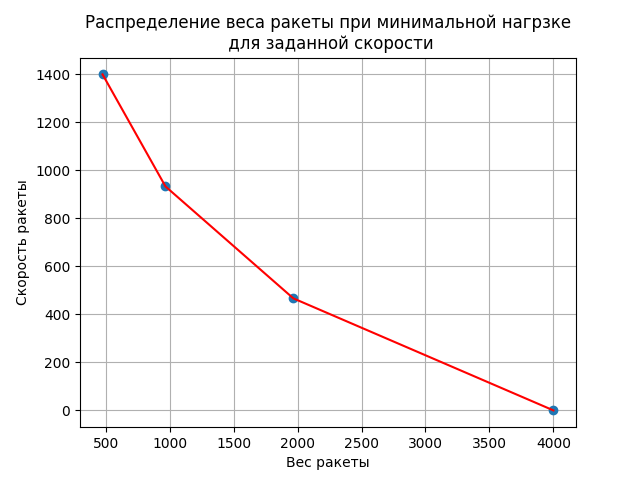
Вес ракеты распределен так (4000.0; 1967.0; 967.9; 476.1), что соответствует нарастанию скорости равными долями (после отделения каждой ступени) в среднем на 460 м/с.
Используем ту же формулу для конечной скорости ракеты, что и в предыдущей задаче:
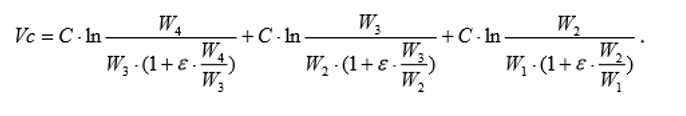
Так как W4 и W1 заданы, то распределением веса ракеты по ступеням W3 и W2 можно максимизировать идеальную конечную скорость Vc при заданном коэффициенте полезной нагрузки ракеты G.
Решение второй задачи на Python
С учётом ранее изложенного, запишем часть листинга до функции цели:
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import time
C=2000 # скорость реактивной струи
e=0.4# коэффициент влияния изменения нагрузки
w4zad=4000# масса ракеты
w1zad=200# масса первой ступени
def f(a):
return np.log(a/(1+e*a))
def Vc1(w3):
return C*f(w4zad/w3)
def Vc2(w3,w2):
return C*f(w3/w2)
def Vc3(w2):
return C*f(w2/w1zad)
start = time.time()
def fun1(x, y):
return -(C*np.log((w4zad/y)/(1+e*(w4zad/y)))+ C*np.log((y/x)/(1+e*(y/x)))+C* np.log((x/w1zad)/(1+e*(x/w1zad))))Построим контурный график функции цели:
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
C=2000 #скорость реактивной струи
e=0.4#коэффициент влияния изменения нагрузки
w4zad=4000# масса ракеты
w1zad=200# масса первой ступени
def fun1(x, y):
return -(C*np.log((w4zad/y)/(1+e*(w4zad/y)))+ C*np.log((y/x)/(1+e*(y/x)))+C* np.log((x/w1zad)/(1+e*(x/w1zad))))
x= np.linspace(500,5000,10000)
y = np.linspace(500,5000,10000)
z=fun1(x,y)
fig = plt.figure('Контурный график функции цели')
ax= Axes3D(fig)
ax.plot(x,y,z,linewidth=1)
plt.show()
Получим контурный график функции цели с отрицательным знаком для смены минимума на максимум:
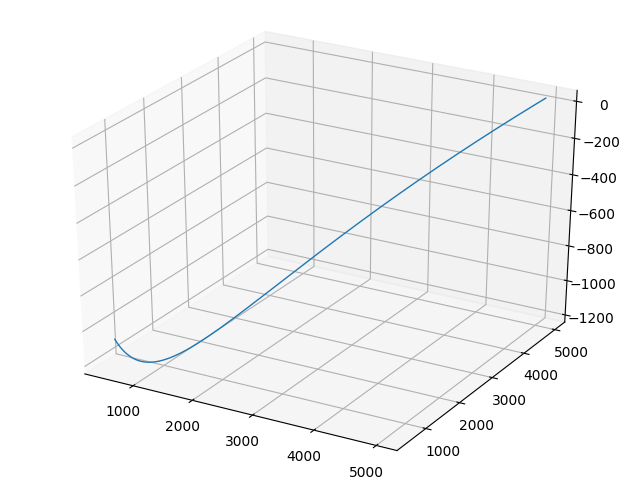
Получили локальный максимум (минимум на графике), поэтому окончательный листинг представим в виде:
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import time
C=2000 #скорость реактивной струи
e=0.4#коэффициент влияния изменения нагрузки
w4zad=4000# масса ракеты
w1zad=200# масса первой ступени
def f(a):
return np.log(a/(1+e*a))
def Vc1(w3):
return C*f(w4zad/w3)
def Vc2(w3,w2):
return C*f(w3/w2)
def Vc3(w2):
return C*f(w2/w1zad)
start = time.time()
def fun1(x, y):
return -(C*np.log((w4zad/y)/(1+e*(w4zad/y)))+ C*np.log((y/x)/(1+e*(y/x)))+C* np.log((x/w1zad)/(1+e*(x/w1zad))))
def fun2(x):
return fun1(*x)
x0 = (1000,2000)
res = minimize(fun2, x0)
stop = time.time()
print ("Время работы оптимизатора:",round(stop-start,3))
print ("Расчётное значение функции цели :",round(res['fun'],3))
w2=round(res['x'][0],3)
w3=round(res['x'][1],3)
v1=round(Vc1(w3),3)
v2=round(Vc1(w3)+Vc2(w3,w2),3)
v3=round(Vc1(w3)+Vc2(w3,w2)+Vc3(w2),2)
print("Изменение веса ракеты -:%s;%s;%s;%s "%(w4zad,w3,w2,w1zad))
print("Изменение скорости ракеты -:%s;%s;%s;%s "%(0,v1,v2,v3))
VES=[w4zad,w3,w2,w1zad]
VC=[0,v1,v2,v3]
plt.title("Распределение веса ракеты при максимальной скорости\n для заданной нагрузки")
plt.plot(VES,VC,'o')
plt.plot(VES,VC,'r')
plt.xlabel("Вес ракеты")
plt.ylabel("Скорость ракеты")
plt.grid(True)
plt.show()В результате получим:
Время работы оптимизатора: 0.016
Расчётное значение функции цели: -1580.644
Изменение веса ракеты -:4000;1473.625;542.889;200
Изменение скорости ракеты -:0;526.873;1053.753;1580.64
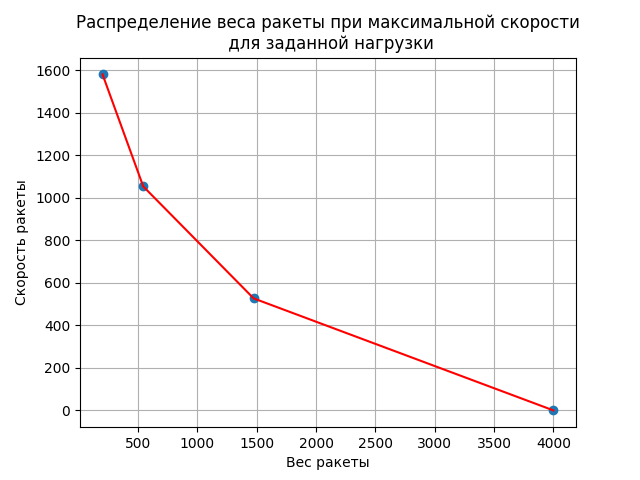
Веса ракеты распределяются так:4000;1473.625;542.889;200, что соответствует нарастанию скорости равными долями (после отделения каждой ступени) на 526.9 м/с.
Выводы
В публикации рассмотрены особенности применения библиотеки scipy. optimize при решении задач оптимизации на примере оптимизации многоступенчатой ракеты. Полученные результаты в части неизменности начальной точки поиска экстремума для переменных и формирования функции цели в привычном пользователю виде будут способствовать расширению области применения свободно распространяемого языка программирования Python.
Всем спасибо за внимание! И главное, чтобы многоступенчатая ракета с не полезной для нас нагрузкой НИКОГДА к нам не прилетела.
Ссылки
- Решение задач нелинейного программирования
- SciPy. Optimize.minimize
