Разбираем самый маленький JPEG в мире
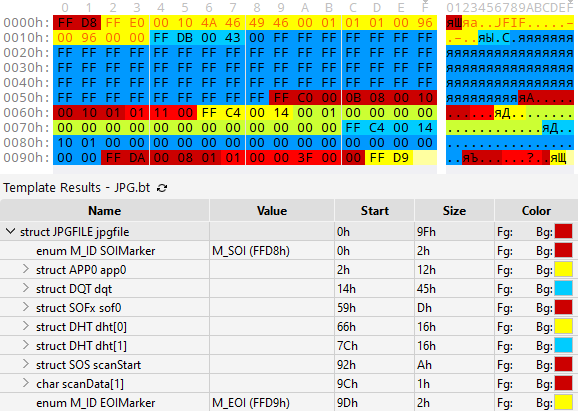
Самый маленький корректный Baseline JPEG (159 байтов)
Недавно на Хабре была опубликована статья Разбираем самый маленький PNG в мире. Интересно, а какой самый маленький файл JPEG? В ответах на StackOverflow и Reddit можно встретить размеры 107, 119, 125, 134, 141, 160 байтов. Все они представляют серый прямоугольник 1 на 1. И кто прав? Все правы, просто такая разница объясняется различными режимами кодирования и степенью строгости соответствия стандарту. Описание всех нюансов разрослось до целой статьи cо всеми необходимыми подробностями для более-менее хорошего знакомства с самыми маленькими jpeg-ами. После краткой теории разберем 159-байтный файл на КДПВ, а затем рассмотрим способы его уменьшения.
Что такое JPEG
Если сильно упростить, то суть кодирования JPEG вот в чем. Каждый блок изображения 8 на 8 пикселей раскладывается в виде взвешенной суммы таких «волняшек» (с помощью DCT-II — разновидностью двухмерного дискретного преобразования Фурье).

Это я сам рисовал в Питоне
Весами являются 64 разночастотных коэффициента, образующих матрицу 8 на 8 (соответственно позициям «волняшек»). Левое верхнее значение представляет константную составляющую — DC-коэффициент. Остальные 63 — AC-коэффициенты. Чем выше частота, тем мельче и тоньше детали изображения за которые она отвечает. И при повышении частоты вклад каждого коэффициента в общую картину становится все более незаметным, что позволяет либо вообще обнулять их, либо «огрублять».
Процесс «огрубления» коэффициентов называется квантованием: каждый коэффициент делится на соответствующее число таблицы квантования и округляется. Рассмотрим, например, таблицу квантования из стандарта (ей соответствует 50% качество сжатия). Как видим, у высокочастотных коэффициентов мало шансов не превратиться в 0.
16 11 10 16 24 40 51 61
12 12 14 19 26 58 60 55
14 13 16 24 40 57 69 56
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99 Полученные коэффициенты записываются с помощью кодирования Хаффмана или арифметического кодирования. Порядок записи зигзагообразный.

Шакалы на сильно сжатой картинке образуются из-за обилия нулевых значений. К примеру, ненулевыми могут оставаться только DC и первые 1–3 AC, которые могут передать разве что примерный градиент.
Режимы
Каждый файл JPEG закодирован одним из 13 способов. Основные характеристики каждого способа:
Режим: Sequential (обычно), Progressive (редко), Hierarchical или Lossless (оба — экзотика)
Алгоритм энтропийного кодирования: Хаффмана (обычно) или арифметический (экзотика)
Разрядность хранимых коэффициентов: 8 (обычно), 12 бит (Extended Sequential — экзотика), 16 бит (только для Lossless — экзотика)
Сразу все эти фичи поддерживает, возможно, только libjpeg. Популярная библиотека libjpeg-turbo таким похвастать не может.
В режиме Sequential все коэффициенты для всего изображения записываются последовательно за один проход. Sequential с кодированием Хаффмана называется Baseline. Думаю, что Baseline используется в более чем 99.999% всех существующих JPEG. Это те, который делает ваш смартфон и графический редактор (по умолчанию).
В режиме Progressive запись осуществляется в несколько проходов. Например, сначала передаются только DC-коэффициенты для всего изображения. Затем AC-коэффициенты с 1-го по 5-й каждого блока. И, наконец, в последнем проходе все оставшиеся. Кроме того, возможно передавать не цельные значения коэффициентов, а, например, в первом проходе — все биты кроме самого младшего, в другом — оставшийся младший бит. Такой подход полезен при медленном соединении так как позволяет быстро передать приблизительное изображение и постепенно улучшать его по мере загрузки.
Режим Hierarchical также многопроходный и еще более вариативный. В самом простом случае изображение уменьшается в 2 раза по вертикали и горизонтали. Полученное изображение кодируется в любом другом режиме (Sequential, Progressive или Lossless) и записывается в файл (или передается по сети). Тем временем кодер проделывает обратные операции: декодирует и растягивает. Разница между восстановленным и исходным изображением так же кодируется в одном из других режимов и записывается в файл. В более сложных случаях уменьшенное в 2 раза изображение подвергается аналогичной процедуре, а потом и еще раз. В конечном итоге получается одна мелкая закодированная картинка и несколько последовательных диффов.
Режим Lossless самый непохожий на остальные, так как не использует преобразование Фурье и является алгоритмом сжатия без потерь. В этом режиме для каждого прохода выбирается предиктор: одна из 8 формул для вычисления предсказания значения пикселя (X) по значениям предыдущих пикселей (A, B, C). Разница между предсказанием и фактическим значением кодируется Хаффманом или арифметическим кодированием.
C B .
A X .
. . .
0: без предсказания
1: X = A
2: X = B
3: X = C
4: X = A + B - C
5: X = A + (B - C)/2
6: X = B + (A - C)/2
7: X = (A + B)/2Структура файла
Общая структура такова:
[Маркер начала изображения]
[Маркер X][Сегмент X]
[Маркер Y][Сегмент Y]
[Маркер Z][Сегмент Z]
...
[Маркер параметров прохода 1][Параметры 1][Энтропийно-кодированный сегмент 1]
[Маркер параметров прохода 2][Параметры 2][Энтропийно-кодированный сегмент 2]
[Маркер параметров прохода 3][Параметры 3][Энтропийно-кодированный сегмент 3]
...
[Маркер конца изображения]Все маркеры — 2 байта вида «FF XX», причем значение XX задает тип маркера и, соответственно, тип сегмента, который следует далее. Сегменты в начале файла (здесь условно обозначены как X, Y, Z… и т. д.) содержат различную метаинформацию. Каждый энтропийно-кодированный сегмент содержит коэффициенты одного прохода.
Самый маленький JPEG
Мы разберем 159-байтный Baseline JPEG. Скорее всего, это файл (точнее один из файлов) минимального размера, который поддерживается всеми декодерами и полностью соответствует стандарту. Но вскоре мы разберем другие примеры и способы уменьшения размера.
Размерность рассматриваемого файла — 16×16, хотя можно заменить на 1×1 как во всех найденных примерах на сторонних ресурсах. Но меньше байтов он занимать не станет, так как кодеры все равно работают с блоками 8×8, а декодеры обрезают до подходящего размера. A так как в нашем примере для блока 8×8 требуется 2 бита, мы можем взять изображение 16×16 (или 32×8), чтобы заполнить единственный байт, в котором хранятся кодированные коэффициенты.
Теперь подробнее из чего состоит файл.
FF D8 Маркер начала изображенияМаркер начала кодированного изображения, найдя который, декодер начинает свой работу. Если дописать в начало файла что-нибудь, то картинка все равно будет корректно восстановлена.
FF E0 Маркер сегмента APP0, назначение которого определяется приложением
00 10 Длина сегмента (16 байтов)
4A 46 49 46 00 Идентификатор "JFIF"
01 02 Старшая (1) и младшая версии (2)
01 Единица измерения плотности (1 - точек на дюйм)
00 96 00 96 Гориз-я (150) и верт-я плотность (150)
00 00 Ширина (0) и высота (0) превьюшки в пикселахСегмент APP0. Вообще таких сегментов может быть много: от APP0 (0xFFE0) до APP15 (0xFFEF), причем не по одному разу каждый. Они используются для различных прикладных нужд, не относящихся к стандарту JPEG. Например для Exif. В нашем случае содержимое описывается спецификацией JFIF. Но об этом позже.
FF DB Маркер таблицы квантования
00 43 Длина сегмента (67 байтов)
00 Разрядность (0 - 8 бит) и идентификатор таблицы квантования (0)
XX ... XX 64 байта значений таблицы квантований 8x8Единственная таблица квантования. В Baseline JPEG она всегда представляет собой 64 однобайтовых значений, заполняющих таблицу 8 на 8. В нашем примере значения могут быть любыми, так как 0 * X = 0.
FF C0 Маркер заголовочного фрейма SOF0
00 0B Длина сегмента (8 байтов)
08 Размерность хранимых коэффициентов (8 битов)
00 10 Высота изображения (16)
00 10 Ширина изображения (16)
01 Количество каналов (1 - только серый)
01 Идентификатор канала (1). Параметры этого канала:
11 Гориз-е и верт-е прореживание (1, 1)
00 Идентификатор таблицы квантования (0)Заголовочный фрейм SOF0 означающий Baseline JPEG. Сегмент содержит:
Размерность коэффициентов — 8 бит. Такая размерность использутся в подавляющем количестве файлов. Другое возможное значение — 12 бит для Extended JPEG, но вы его вряд ли встретите, оно поддерживается единичными кодерами.
Размер изображения — 16 на 16 пикселей.
Один канал. Стандарт не регламентирует его цвет, но единственный канал всегда рассматривается декодерами как серый. В случае нескольких каналов интерпретируются идентификаторы каналов. Например, для Y, Cb, Cr — просто 1, 2 и 3, для R, G, B — 82, 71, 66, то есть 'R', 'G', 'B' в ASCII. Почти во всех встречающихся jpeg-ах используется цветовая модель YCbCr. У нее один канал яркости и 2 цветоразностных канала для синего и красного.
Прореживание не используется, так как для одного канала оно бессмысленно. Но обычно Cb, Cr уменьшают в 2 раза по горизонтали и вертикали, так что каждые 4 пикселя (2 на 2) заменяются одним со средним значением.
Идентификатор таблицы квантования для этого канала равен 0, мы рассмотрели ее ранее. Почти во всех встречающихся jpeg-ах используется 2 таблицы: одна для канала Y, другая (общая) для Cb, Cr.
FF C4 Маркер таблицы Хаффмана
00 14 Длина сегмента (20 байтов)
00 Класс таблицы (0 - DC коэф-ы) и идентификатор таблицы (0)
01 Количество кодов (1) длины 1
00 Количество кодов (0) длины 2
... ...
00 Количество кодов (0) длины 16
00 Значение кода (0, того единственного с длиной 1)
FF C4 Маркер таблицы Хаффмана
00 14 Длина сегмента (20 байтов)
10 Класс таблицы (1 - AC коэф-ы) и идентификатор таблицы (0)
01 Количество кодов (1) длины 1
00 Количество кодов (0) длины 2
... ...
00 Количество кодов (0) длины 16
00 Значение кода (0, того единственного с длиной 1)2 таблицы Хаффмана. Одна из них для кодирования DC-коэффициентов DCT-преобразования, другая — для AC. Сегмент хранит только количество кодов для каждой длины (от 1 до 16 битов) и значения кодов, но не сами коды. Этой информации достаточно, чтобы построить дерево Хаффмана. В нашем случае в каждой таблице только по одному коду 0 со значением 0.
FF DA Маркер параметров прохода
00 08 Длина сегмента (8 байтов)
01 Количество каналов прохода (1)
01 Для канала с идентификатором (1):
00 Идентификаторы таблиц Хаффмана для DC и AC (0, 0)
(Параметры, актуальные только для Progressive или Lossless)
SS SE Progressive: диапазон коэффициентов (с индексами от SS до SE),
записываемых в этом проходе
Lossless: предиктор (SS)
HL Progressive: диапазон битов (с индексами от H до L)
значений коэффициентов для записи в этом проходе
H должен быть равен нулю в первом проходе
для каждой новой партии коэффициентовПараметры очередного прохода, задающие используемые далее идентификаторы таблиц Хаффмана. В файле каждый такой сегмент расположен перед данными соответствующего прохода. Sequential JPEG использует только один проход, поэтому такой сегмент тоже один. Параметры определяют какие каналы передаются в текущем проходе, таблицы Хаффмана (отдельно для DC и AC), подмножество коэффициентов и их диапазон битов. Значения SS, SE, H, L не имеют смысла для Sequential, но они должны быть равны 0, 63, 0, 0, видимо, чтобы подчеркнуть, что коэффициенты передаются сразу полностью.
00 Энтропийно-кодированный сегментОписание в следующем разделе.
FF D9 Маркер конца изображенияМаркер конца изображения. Пожалуй, все декодеры справляются и без этого маркера. Но по стандарту он обязателен.
Декодирование примера
Структура сегмента имеет примерно такой вид:
[Код][Коэффициент][Код][Коэффициент]...Хм, зачем нужны коды Хаффмана, если коэффициенты лежат в открытом виде? Дело в том, что мы не знаем битовую длину коэффициента, но она (и другая информация) хранится в значении кода. Поэтому, чтобы читать энтропийно-кодированный сегмент, декодеру требуются таблицы Хаффмана. Таблица состоит из префиксных кодов различной длины (от 1 до 16 битов) и их значений.
Как было сказано ранее, изначально известны только количество кодов для каждой длины (от 1 до 16 битов) и их значения, но не сами коды. Чтобы найти коды можно создать пустое бинарное дерево и добавлять очередное значение кода как можно левее так, чтобы уровень глубины узла был равен длине кода. Путь в дереве и будет являться кодом.
Обе таблицы из примера тривиальные с единственным кодом 0 и его значением 0.
Чуть более сложный пример
Сегмент с таблицей Хаффмана какого-то файла:
FF C4
00 1A
10
01 00 02 03 01 00 00 00 00 00 00 00 00 00 00 00
01 00 12 03 11 31 21Упростить интерпретацию можно с помощью JPEGSnoop:
Destination ID = 0
Class = 1 (AC Table)
Codes of length 01 bits (001 total): 01
Codes of length 02 bits (000 total):
Codes of length 03 bits (002 total): 00 12
Codes of length 04 bits (003 total): 02 11 31
Codes of length 05 bits (001 total): 21
Codes of length 06 bits (000 total):
Codes of length 07 bits (000 total):
Codes of length 08 bits (000 total):
Codes of length 09 bits (000 total):
Codes of length 10 bits (000 total):
Codes of length 11 bits (000 total):
Codes of length 12 bits (000 total):
Codes of length 13 bits (000 total):
Codes of length 14 bits (000 total):
Codes of length 15 bits (000 total):
Codes of length 16 bits (000 total):
Total number of codes: 007По этим данным строится такое дерево. В кружках — значения кодов, под кружками — сами коды (мы получили их, пройдя путь от вершины до каждого узла)

Младшие 4 бита значения — битовая длина коэффициента. Старшие 4 бита — количество нулевых AC коэффициентов, которые нужно расположить перед рассматриваемым. Это эффективно, потому что матрица может быть сильно разрежена (в смысле ненулевых значений).
Фотокамеры обычно (всегда?) используют готовые таблицы Хаффмана. В приличных редакторах, как правило, есть опции вроде «Optimize» или «Optimize Huffman» для генерации наиболее подходящих таблиц для конкретного изображения.
Чтение энтропийно-кодированного сегмента
Наш сегмент состоит из 8 нулевых битов. Он читается следующим образом.
Создается матрица 8 на 8.
Читается первый бит и проверяется таблица Хаффмана для DC-коэффициентов. Да, такой код там есть. Его значение 0. Это значит, что значение DC-коэффициента равно 0. Оно присваивается элементу матрицы с индексом [0, 0].
Читается второй бит и проверяется таблица Хаффмана для AC-коэффициентов. Аналогично получается 0. Значение 0 — особое, означающее, что нужно завершить чтение и заполнить все оставшиеся значения матрицы нулями.
Читаем оставшиеся 6 битов и, в конечном итоге, получаем 4 матрицы 8×8 заполненных нулями. Значения каждой матрицы — коэффициенты дискретного косинусного преобразования. Выполнив обратное преобразование, получаем все те же нули. Далее умножаем почленно каждый элемент матрицы на соответствующий элемент матрицы квантования, что опять приводит к одним нулям. Поэтому в примере значения могут быть произвольными. Наконец, прибавляем по 128 к каждому элементу и получаем 4 серых квадрата 8 на 8.
Другие примеры маленьких JPEG-ов
Описанный 159-байтный файл выглядит слишком большим на фоне остальных. Основные отличия следующие.
Использование арифметического кодирования. Файл получается меньше, но… Во-первых, его почти никто не поддерживает (в том числе браузеры). Во-вторых, я с ним не разбирался, поэтому не описываю :)
[Минус 2 байта] Удален маркер конца изображения. Это точно не соответствует стандарту. Хотя декодерам норм.
[Минус 18 байтов] Удален сегмент с заголовком JFIF. Стандарт JPEG описывает непосредственно кодек. JFIF описывает формат файла, содержимое которого закодировано JPEG-ом. То есть jpeg-файлы фактически являются jfif-файлами. Единственное жесткое требование JFIF — наличие специального заголовка. Хотя декодерам опять-таки норм и без него.
[Минус 22 байта] Использование прогрессивного режима. Фича прогрессивного режима — возможность частичной записи коэффициентов в каждом проходе. Автор одного из маленьких jpeg-ов предлагает ограничиться одним проходом с записью только DC-коэффициентов. Тогда понадобится только одна таблица Хаффмана. Это действительно сработало. Я не нашел в спецификации запрета такого трюка, но не нашел и явного разрешения.
Если вам понравилось и хочется почитать что-нибудь про JPEG, то подписывайтесь на мой телеграм-канал (блин, забыл что его нет) можете перейти к моей старой статье Изобретаем JPEG, чтобы интуитивно понимать этот алгоритм.
