Рассеяние света в атмосфере в менее чем четырёх килобайтах18.06.2018 07:17

В этой краткой заметке будет рассказано о том, как устроена модель атмосферного рассеяния света в нашей последней 4к интре Appear by Jetlag, party-версия которой заняла почётное 12-е место в 4k intro compo на демопати Revision 2018 в апреле этого года.

Cкачать бинарник бесплатно без смс можно здесь.

Если, однако, у вас не Виндовс, или нет мощной современной видеокарты, то есть утешительный утупчик:


Музыку к этой работе написал keen, используя 4klang. За мной же остался весь код и визуальный ряд.

Здесь будет рассказано только о модели рассеяния света. Остальные вещи, как то: инструментарий, модель города, модель освещения и материалов, не затрагиваются. Смелых могу отправить читать исходники, или смотреть записи того, как я часами туплю — большая часть разработки попала на видео.

Работа над этой работой началась с осознания, что основная на-полный-рабочий-день работа не оставляет времени на работу над полноценной 4к работой — на дворе уже почти середина марта, до Ревижена остаётся пара-тройка недель.
Остаётся лишь придумать что-нибудь достаточно простое для быстрого, на пару вечеров, компо-филлера. Делать очередной тупо реймарч — не уважать зрителя, поэтому я вспомнил, что несколько лет назад доводилось делать шейдер с рассеянием, и он был довольно простым, компактным и в то же время допустимо красивым, хотя и довольно медленным.

В ходе недолгого обсуждения я настоял на своём, и мы решили остановиться на следующем: сделать ландшафт, залитый рассеянным светом, с закатом, облаками и сумеречными лучами (TIL как переводится выражение «god rays»). Для того, чтобы не задирать количество шагов по атмосфере до совсем неинтерактивных величин, придётся сильно дребезжать лучами (дворовый такой Монте-Карло метод), что породит видимый шум. Но не беда, если камеру двигать и сцену менять медленно и пустить эмбиент-трек, то можно безболезненно смешивать соседние кадры и темпорально сглаживать этот шум.

Keen написал музыку довольно быстро — она была практически готова за две недели до Ревижена. Меня, однако, серьёзно подкосил грипп — со скорой и инфекционкой — поэтому я практически не начинал работать над шейдером вплоть до того момента, пока в более-менее как-то живом состоянии не попал на самолёт до Франкфурта. Прототип этой модели рассеяния был написан уже в воздухе.

Party-версию интры мы уже на скорую руку собирали из песка и слюней на самой пати в течение нескольких остававшихся часов до дедлайна (и, наверное, парочки — после; D), пока я параллельно отходил от гриппа, недосыпа, многочасовых перелётов, а так же постоянно отвлекался на участие в Shader showdown livecoding compo.

Версия, показанная на большом экране, содержала очень много артефактов и лишь рудиментарную геометрию города на основе диаграммы Вороного со случайными высотами.

В общем, 12-е место — это довольно щедро.

Финальная версия, продемонстрированная выше, была сделана уже позднее и в более расслабленном режиме по 1–2 вечера в неделю в течение месяца. В общей сложности на работу ушло около 40–50 часов труда.

(Примечание: я не занимаюсь программированием графики профессионально. Это — моё маленькое уютное хобби на хорошо, если сотню-другую очень расфокусированных под пивовино часов в год. Поэтому не нулевая вероятность того, что некоторые вещи ниже описаны и/или названы неправильно. Дяденьки, бейте!)

Модель рассеяния позаимствована из статьи «High Performance Outdoor Light Scattering Using Epipolar Sampling» товарища Egor Yusov, опубликованной в книге GPU Pro 5, с полностью выкинутым эпиполярным семплингом.


Физическая модель

Фотоны солнышка бомбардируют атмосферу земли и взаимодействуют с частицами воздуха. Фотон может быть рассеян частицей, что влечёт за собой изменение направления фотона, или он может быть поглощён, что означает, что фотон потерян, а его энергия была преобразована в какую-то иную форму.
Оба процесса вероятностные и зависят в частности от плотности частиц и энергии фотона (которая соответствует его цвету).

На пальцах, «красные» фотоны имеют более низкую вероятность взаимодействия с воздухом, поэтому они преодолевают толщу атмосферы относительно нетронутыми.
«Голубые», однако, имеют более высокую вероятность рассеяния, отчего они могут менять направление неоднократно и преодолевать значительные расстояния в атмосфере, прежде чем достигнут (или нет) наблюдателя.

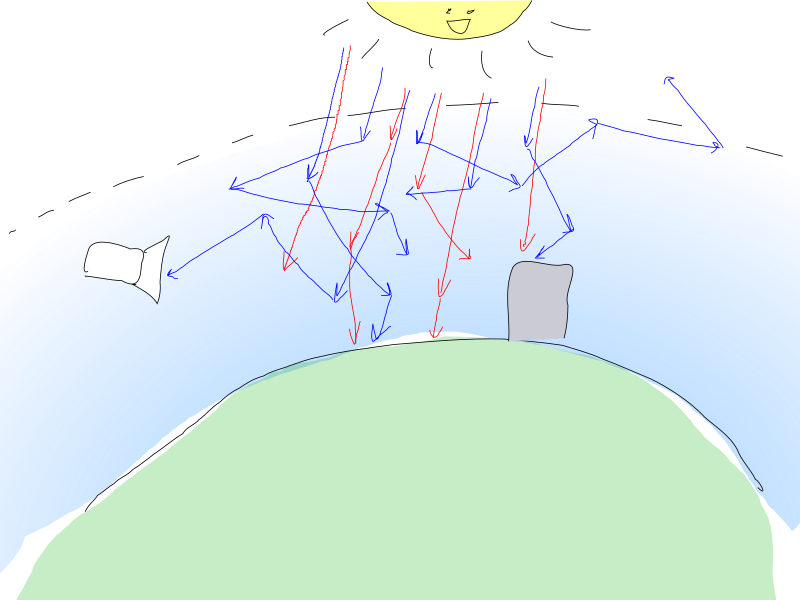
image

Интересующие нас параметры взаимодействия света с воздухом следующие:

Предполагается, что воздух состоит из двух типов частиц, рассеяние на которых происходит независимо: молекулы (Рэлеевская модель) и аэрозоли (относительно крупные сферические частицы, Mie scattering в англоязычной литературе). Модели отличаются только разными значениями для параметров выше.

Для обеих моделей считается, что плотность соответствующих частиц экспоненциально убывает с высотой: $\rho = \rho_0e^{-\frac{h}{H}}$, где $\rho_0$ — плотность на уровне моря. Коэффициенты $\beta$ пропорциональны $\rho$, и их значения ниже даны для уровня моря.


Рэлеевская модель


  • $p_R(\alpha) = \frac{3}{16\pi}(1+\cos^2(\alpha))$ [Nishita et al. 93, Preetham et al. 99]
  • $\beta_R^a = 0$
  • $\mathbf{\beta_R^e} = \mathbf{\beta_R^s} = (5.8, 13.5, 33.1)_{rgb}10^{-6}m^{-1}$ [Riley et al. 04, Bruneton and Neyret 08]
  • $H_R = 7994m$ [Nishita et al. 93]


Аэрозоли


Приближение одиночного рассеяния

Приближение рассеяния строится на пускании луча из каждого пикселя камеры и расчете, сколько света из атмосферы должно попасть из этого направления. Каждому лучу соответствуют все три RGB компоненты света, будто вдоль этого луча летят три фотона с соответствующими энергиями.

Свет, достигающий камеры, формируется следующими процессами в толще воздуха:


  • Врассеяние (TIL, что фиг узнаешь, как переводится in-scattering). Добавляется свет, испущенный солнцем, который вероятностным образом рассеивается на угол, соответствующий направлению на камеру.
  • Поглощение. Свет, уже летящий вдоль луча, поглощается воздухом.
  • Рассеяние. Свет, уже летящий вдоль луча, теряется на рассеяние в других направлениях.

Из соображений производительности считаем, что свет может от рассеяния попасть в направление на камеру только один раз, и всем остальным светом (который был рассеян более одного раза) можно пренебречь. Этого делать не рекомендуют для сумерек, но что поделать.

Этот подход изображен на следующем прекрасном изображении (я старался!):

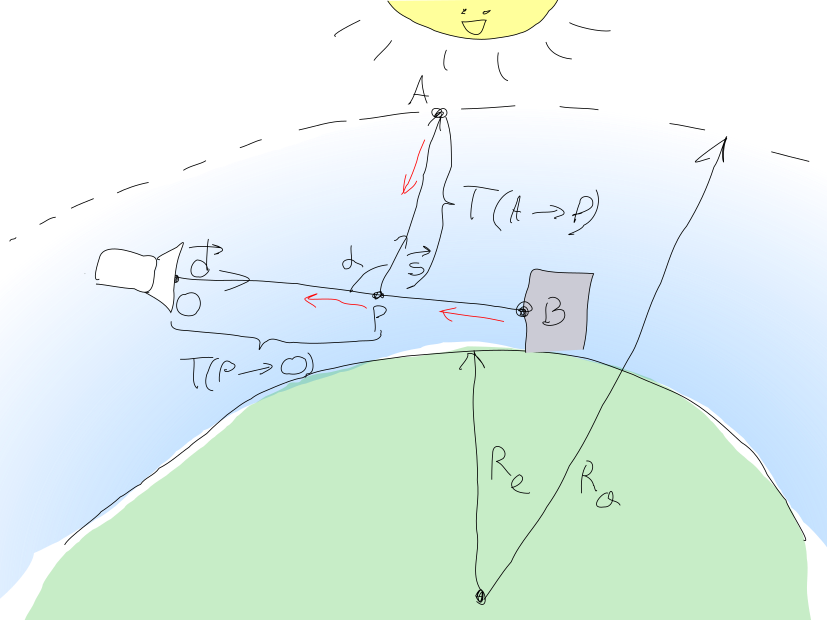
image

Таким образом, количество света, которое должно быть зарегистрировано пикселем камеры в точке $O$ может быть рассчитано как сумма $\mathbf{L} = \mathbf{L_{in}} + \mathbf{L_{BO}}$, где $\mathbf{L_{in}}$ — врассеянный свет от солнца, а $\mathbf{L_{BO}}$ — количество света от точки $B$ объекта геометрии сцены, достигающего $O$.


Свет геометрии

$\mathbf{L_{BO}} = \mathbf{L_O} e ^ {-\mathbf{T}(B \rightarrow O)}$, где $\mathbf{L_O}$ — это свет, испущенный из точки $B$ в направлении камеры.

$\mathbf{T}(B \rightarrow O)$ называется оптической толщиной среды между точками $B$ и $O$, и вычисляется следующим образом:

$\mathbf{T}(B \rightarrow O) = \int_B^O(\beta_M^e(s) + \mathbf{\beta_R^e}(s))ds$

Принимая во внимание, что члены $\beta$ состоят из константы уровня моря и переменной плотности, это выражение можно преобразовать до:

$\mathbf{T}(B \rightarrow O) = \beta_M^e \cdot \int_B^O \rho_M(s) ds + \mathbf{\beta_R^e} \int_B^O \rho_R(s) ds = \bar{\mathbf{\beta}} \cdot \bar{T_\rho}(B \rightarrow O)$

Обратите внимание, что я специально не раскрываю $\rho$, потому что мы будем их менять в дальнейшем при добавлении облаков. Также обращаю внимание на то, что $\beta$ — вектора RGB (по крайней мере $\mathbf{\beta_R}$ имеют разные значения для RGB-компонент, а $\beta_M$ — вектор просто для консистентности). Члены с $\rho$ под интегралом — скаляры.


Солнечный свет

Солнечный свет $\mathbf{L_{in}}$ рассчитывается интегрированием по всем точкам $P$ вдоль отрезка $OB$ и накоплением всего входящего солнечного света, рассеивающегося в сторону камеры и затухающего в толще $\mathbf{T}(P \rightarrow O)$.

Количество солнечного света, достигающего точки $P$, вычисляется по аналогичной формуле $\mathbf{L_P} = \mathbf{L_{sun}}e^{-T(A \rightarrow P)}$, где $\mathbf{L_{sun}}$ — яркость солнца, а $A$ — точка, в которой луч из точки $P$ в направлении солнца $\vec{s}$ покидает атмосферу. Доля этого света, которая будет рассеяна в направлении камеры, составляет $\mathbf{L_P} \cdot (\mathbf{\beta_R^s}(s)p_R(\alpha) + \beta_M^s(s) p_M(\alpha))$.

Итого получим:

$\mathbf{L_{in}} = \int_B^O \mathbf{L_P}(s) \cdot (\beta_M^s(s) p_M(\alpha) + \mathbf{\beta_R^s}(s)p_R(\alpha)) \cdot e ^ {-\mathbf{T}(P(s) \rightarrow O)} ds$

Можно заметить, что:


  • $\alpha$ является константой для каждого пикселя-луча камеры (считаем, что солнце бесконечно далеко и лучи от него параллельны)
  • Коэффициенты $\beta$ состоят и констант уровня моря и функций плотности $\rho(s)$
  • Функции $p(\alpha)$ имеют общие множители для обоих процессов рассеяния

Это позволяет преобразовать выражение в:

$\mathbf{L_{in}} = \mathbf{L_{sun}} (1+\cos^2(\alpha)) (\frac{\frac{1}{4\pi}\frac{3(1-g^2)}{2(2+g^2)}}{(1 + g^2 - 2g\cos(\alpha))^\frac{3}{2}}\beta_M^s \cdot \mathbf{I_M} + \frac{3}{16\pi} \mathbf{\beta_R^s} \cdot \mathbf{I_R})$

где

$\mathbf{I_M} = \int_B^O \rho_M(s) e^{-\mathbf{T}(A \rightarrow P(s)) - \mathbf{T}(P(s) \rightarrow O)} ds$

$\mathbf{I_R} = \int_B^O \rho_R(s) e^{-\mathbf{T}(A \rightarrow P(s)) - \mathbf{T}(P(s) \rightarrow O)} ds$

$I_M$ и $I_R$ отличаются только функциями плотности, их экспоненты при этом одинаковы.

Эти интегралы никому так и не удалось вычислить аналитически, поэтому придётся считать численно, с помощью рэймарчинга (как, говорится в исходных публикациях, делать нельзя!).


Численное интегрирование

Из соображений размера и лени считать будем как можно более тупо: $\int_A^B f(x) dx \approx \frac{\left |B - A \right |}{N} \sum_{i=0}^N f(A + i \cdot \frac{\vec{B - A}}{N})$

Маршировка по лучу будет производиться в противоположном потоку света направлении: от точки камеры $O$ до пересечения луча с геометрией $B$. Отрезок $O \rightarrow B$ делится на $N$ шагов.

Прежде чем запустить марш, инициализируем переменные:


  • vec2 (две отдельные компоненты, для Релеевского и аэрозольного рассеяний) общая накопленная оптическая толщина $\mathbf{T_\rho}(P(s) \rightarrow O)$
  • vec3 (RGB) $\mathbf{I_M}$, $\mathbf{I_R}$

Далее для точки $P_i$ каждого шага между $O$ и $B$:


  1. Испутим луч $\vec{s}$ в направлении солнца и получим точку $A_i$ выхода этого луча из атмосферы.
  2. Вычислим толщину $\mathbf{T}(A \rightarrow P_i)$, сначала рассчитав $\int_A^{P_i}\rho_M(s)ds$ и $\int_A^{P_i}\rho_R(s)ds$ с помощью такого же рэймарчинга (с количеством шагов M), а затем перемножим полученные слагаемые с соответствующими константами $\beta_M^e$ и $\mathbf{\beta_R^e}$.
  3. Вычислим толщину $\mathbf{T_\rho}(P_i \rightarrow O) = \mathbf{T_\rho}(P_{i-1} \rightarrow O) + \rho_i(s) \cdot ds$
  4. Аккумулируем $\mathbf{I_R}$ и $\mathbf{I_M}$, используя эти значения

Финальный цвет после рэймарчинга вычисляется суммой слагаемых:


  1. Слагаемое $\mathbf{L_{BO}}$ получить тривиально: переменная, содержавшая $\mathbf{T_\rho}(P_i \rightarrow O)$ содержит значение $\mathbf{T_\rho}(B \rightarrow O)$, поскольку $P_i$ достигла $B$.
  2. Перемножением $\mathbf{I_R}$ и $\mathbf{I_M}$ на соответствующие константы и сложением результата вычисляется $\mathbf{L_{in}}$


Простое рассеяние без никто

Немного причёсанные и откомментированные исходники рассеяния, взятые (почти) напрямую из самой интры: 

const float R0 = 6360e3; // Радиус поверхности земли
const float Ra = 6380e3; // Радиус верхней границы атмосферы
const vec3 bR = vec3(58e-7, 135e-7, 331e-7); // Рэлеевский коэффициент рассеяния
const vec3 bMs = vec3(2e-5); // Аэрозольный коэффициент рассеяния
const vec3 bMe = bMs * 1.1;
const float I = 10.; // Яркость солнца
const vec3 C = vec3(0., -R0, 0.); // Координаты центра земли, точка (0, 0, 0) находится на поверхности

// Функция плотностей
// Возвращает vec2(rho_rayleigh, rho_mie)
vec2 densitiesRM(vec3 p) {
    float h = max(0., length(p - C) - R0); // Высота от поверхности
    return vec2(exp(-h/8e3), exp(-h/12e2));
}

// Пересечение луча и сферы, используется для вычисления расстояния покидания лучом атмосферы
float escape(vec3 p, vec3 d, float R) {
    vec3 v = p - C;
    float b = dot(v, d);
    float det = b * b - dot(v, v) + R*R;
    if (det < 0.) return -1.;
    det = sqrt(det);
    float t1 = -b - det, t2 = -b + det;
    return (t1 >= 0.) ? t1 : t2;
}

// Вычисление интеграла плотности оптической глубины для отрезка длины `L` из точки `p` в направлении `d`
// Интегрирует за `steps` шагов
// Возвращает vec2(depth_int_rayleigh, depth_int_mie)
vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) {
    vec2 depthRMs = vec2(0.);
    L /= steps; d *= L;
    for (float i = 0.; i < steps; ++i)
        depthRMs += densitiesRM(o + d * i);

    return depthRMs * L;
}

// Глобальные переменные (в основном -- из соображений размера)
vec2 totalDepthRM;
vec3 I_R, I_M;

// Направление на солнце
vec3 sundir;

// Рассчитать количество солнечного света, рассеиваемого в направлении `-d` отрезка длиной `L` из точки `o` в направлении `d`.
// `steps` -- количество шагов интегрирования
void scatterIn(vec3 o, vec3 d, float L, float steps) {
    L /= steps; d *= L;

    // Из точки O в B
    for (float i = 0.; i < steps; ++i) {

        // P_i
        vec3 p = o + d * i;

        vec2 dRM = densitiesRM(p) * L;

        // Накопление T(P_i -> O)
        totalDepthRM += dRM;

        // Вычисление суммы оптической глубины T(P_i ->O) + T(A -> P_i)
        // scatterDepthInt() вычисляет скалярную часть T(A -> P_i)
        vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.);

        vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y);

        I_R += A * dRM.x;
        I_M += A * dRM.y;
    }
}

// Готовая функция рассеяния
// O = o -- начальная точка
// B = o + d * L -- конечная точка
// Lo -- цвет геометрии в точке B
vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) {
    totalDepthRM = vec2(0.);
    I_R = I_M = vec3(0.);

    // Вычисление T(P -> O) and I_M and I_R
    scatterIn(o, d, L, 16.);

    // mu = cos(alpha)
    float mu = dot(d, sundir);

    // Затухание цвета геометрии сцены
    return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y)

    // Солнечный свет
        + I * (1. + mu * mu) * (
            I_R * bR * .0597 +
            I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5));
}

Зазыкать на шейдертое


Облака

Неплохо, но такую картинку можно было бы также получить гораздо проще каким-нибудь хитрым нагромождением градиентов.

Обманным путём же получить облака и god rays значительно сложнее. Давайте добавим.

Идея заключается в приближении облаков аэрозолями и модификации только функции плотностей densitiesRM(). Это может быть не настолько физически корректно, как хотелось бы (понятия не имею, как на самом деле приближается рассеяние света в облаках в компьютерной графике).

// Верхняя и нижняя границы атмосферы
const float low = 1e3, hi = 25e2;

// vec4 noise24(vec2 v) -- просто читает значения из шумовой текстуры
// float t -- время

float noise31(vec3 v) {
    return (noise24(v.xz).x + noise24(v.yx).y) * .5;
}

vec2 densitiesRM(vec3 p) {
    float h = max(0., length(p - C) - R0);
    vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.);

    // Облака ограничены высотой (оптимизация)
    if (low < h && h < hi) {
        vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.));

        // Вся эта мешанина аккуратно написана от балды с одной целью: чтобы интра выглядела приемлемо
        retRM.y +=
            250. *
            step(v.z, 38.) *
            smoothstep(low, low + 1e2, h) *
            smoothstep(hi, hi - 1e3, h) *
            smoothstep(.5, .55, // ключевая часть: многооктавный шум
                .75 * noise31(v)
                + .125 * noise31(v*4. + t)
                + .0625 * noise31(v*9.)
                + .0625 * noise31(v*17.)-.1
            );
    }

    return retRM;
}

Вопреки ожиданиям, получаем не красивые облака, сладкую победу и поклонниц, а артефакты. Попытка в лоб поднять количество шагов артефакты убирает не полностью, однако значительно портит производительность.

Решения костыли, которыми подтыкается интра:


  • Самые неприятные артефакты на горизонте прячутся за горами
  • Облака добавляются только вблизи камеры
  • Добавляется Монте-Карловщина, каждый маршируемый луч сдвигается на случайное смещение: for (float i = pixel_random.w; i < steps; ++i). Это добавляет тот самый шум, который приходится темпорально сглаживать смешиванием подряд идущих кадров.

  • Увеличивается количество шагов для зон, требующих большего количества деталей (например, слой с облаками). Именно для этого сделано такое нелепое разделение функций на scatterImpl() и scatterDepthInt(): 

    // В цикле функции scatterIn()
    vec2 depthRMsum = totalDepthRM;
    float l = max(0., escape(p, sundir, R0 + hi));
    if (l > 0.) // под облаками 16 шагов
        depthRMsum += scatterDepthInt(p, sundir, l, 16.);
    // над облаками достаточно и 4-х
    depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.);

    // в функции scatter()
    // ближайшие 10км получают больше шагов
    float l = 10e3;
    if (L < l)
        scatterIn(o, d, L, 16.);
    else {
        scatterIn(o, d, l, 32.);

        // 8 шагов -- достаточно для дальних расстояний
        scatterIn(o+d*l, d, L-l, 8.);
    }


Совмещение с геометрией сцены

В результате традиционного рэймарчинга функций расстояния и затенения уже получено расстояние L до точки B и цвет пикселя Lo. Эти значения просто подставляются в функцию scatter(). Если луч не упёрся в геометрию и покинул сцену, тогда цвет Lo нулевой, а L рассчитывается с помощью escape() — считается, что луч покинул атмосферу.

Вроде всё.

… На самом деле конечно не всё. Довольно большая боль теперь притереть все части друг к другу так, чтобы оно в целом выглядело правдоподобно. Просто куча возни с подкручиванием параметров, геометрии сцены, шумовых функций, траектории и ракурса камеры. Боюсь, у меня здесь нет хороших советов, кроме как рекомендации много часов итерировать и биться головой о стену.


Минификация

После обработки shader minifier’ом конечный шейдерный код рассеяния имеет размер около 1500 байт. Crinkler ужимает его до ~700 байт, что составляет примерно 30% всего шейдерного кода.

Я не умею в компьютерную графику.

© Habrahabr.ru