Работа с фреймворком итеративной обработки графов Giraph на примере RBM15.08.2016 14:18

The Indifferent by xetobyte

Всем привет. В предыдущей статье мы рассказали, как создавать свои приложения под фреймворк Giraph (надстройка над системой обработки данных Hadoop), и обещали подробно рассмотреть, как работать с Giraph, на примере алгоритма обучения Restricted Boltzmann Machine. Итак, в какой-то момент группа сегментации аудитории департамента рекламных технологий Mail.Ru Group столкнулась с необходимостью подобрать инструмент для быстрого анализа графов, и по целому ряду причин (читайте ниже) наше внимание привлекла система Apache Giraph.

Чтобы понять, насколько данная система удобна/производительна/стабильна и т. д., двум участникам лаборатории Техносферы Mail.Ru Александру Щербакову и Павлу Коваленко было выдано задание исследовать работу с Giraph на примере алгоритма обучения Restricted Boltzmann Machine и попытаться его максимально ускорить. На этой задаче ребята смогли лучше понять тонкости настройки Giraph и получить практический опыт работы с open source проектами.

Ниже мы подробно разберём вариант реализации алгоритма обучения ограниченной машины Больцмана (Restricted Boltzmann Machine, RBM) с помощью фреймворка Giraph, который, в свою очередь, является надстройкой над Hadoop. Будут рассмотрены основные аспекты работы с Giraph, а также некоторые «фишки» и методы тюнинга производительности данного фреймворка. О том, что такое Giraph, и как создать на нём свой первый проект, вы можете прочитать в предыдущей статье.

План статьи
1. RBM и Giraph
    1.1. Краткое описание RBM
    1.2. Giraph
    1.3. RBM и Giraph
2. Управление исполнением compute-методов, worker context
    2.1. Параметры для запуска
    2.2. Обзор деятельности мастера
    2.3. Использование WorkerContext и хранящихся в нём параметров в нейронах
3. Обзор инициализирующих классов
4. Описание общего класса для нейронов
5. Классы нейронов
    5.1. VisibleNeuronZero
    5.2. HiddenNeuronFirst
    5.3. VisibleNeuronFirst
    5.4. NeuronDefault
    5.5. VisibleNeuronLast
    5.6. HiddenNeuronLast
    5.7. VisibleNeuronOneStep
6. Обзор вспомогательных классов
    6.1. JSONWritable
    6.2. RBMInputFormat
7. Оптимизации
    7.1. Хранение рёбер
    7.2. Использование векторных операций
8. Future work
9. Заключение
10. Литература1. RBM и Giraph

1.1. Краткое описание RBM

В данной статье мы ограничимся только фактами, которые необходимы для понимания происходящего, подробнее об RBM вы можете прочитать здесь или здесь.

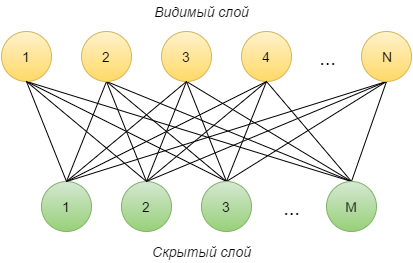
Ограниченная машина Больцмана (Restricted Boltzmann Machine, RBM) — это нейронная сеть, состоящая из двух слоёв: видимого и скрытого. Каждый видимый нейрон i соединён с каждым скрытым j, причём изначально соединяющее их ребро имеет случайный вес wij. Также каждый нейрон имеет параметр «смещение» (видимого слоя — ai, скрытого — bi). Количество нейронов на видимом слое обозначается N, на скрытом — M.

Опишем, как работает такая сеть.

Возьмём некоторый вектор v (0) из обучающей выборки в качестве начальных значений активации нейронов видимого слоя.
На скрытом слое считается вектор h (1) как линейная комбинация значений вектора v (0) с весами w с последующим применением сигмоидальной функции активации: , где — сигмоидальная функция активации. Далее hj = 1 с вероятностью и 0 в противном случае, иначе говоря, проведём семплирование.
Далее по вектору h (1) можно найти новое значение вектора v (1) по аналогичным формулам: .

Шаги 2—3 будем повторять k раз. В итоге получим векторы v (k) и h (k).

Ограниченную машину Больцмана можно рассматривать как метод нелинейного преобразования признакового пространства. Исходный вектор v мы описываем вектором h по формулам, представленным выше. По вектору h мы можем с некоторой точностью восстановить исходный вектор v. Таким образом, вектор v (k) — это результат применения k раз операций преобразования и восстановления к вектору v (0). Логично потребовать, чтобы выходной вектор v (k) был как можно ближе к v (0). Это будет означать, что вектор x можно представить вектором y с минимальными потерями точности.

Будем минимизировать отклонение v (k) от v (0) методом обратного распространения ошибки. Разобьём всю обучающую выборку на батчи — подвыборки фиксированного размера T. Для каждого батча будем находить значения активации, градиенты и обновлять значения весов и смещений. Пусть текущий батч состоит из объектов zi, i = 1… T. Для каждого из них найдём v (j) (zi) и h (j) (zi), j = 1… k. Тогда получим [1, 2] следующие формулы для изменения параметров сети:

где η — темп обучения (learning rate).

Один прогон алгоритма по всем батчам назовём одной эпохой обучения. Для получения лучшего результата имеет смысл провести несколько (K) эпох обучения, чтобы каждый батч был использован K раз для вычисления градиентов и обновления параметров сети. По сути, мы получили алгоритм стохастического градиентного спуска по переменным w, a и b для минимизации среднего по объектам выборки отклонения v (k) от v (0).

1.2. Giraph

Giraph — это система итеративной обработки больших графов, работающая поверх системы распределённой обработки данных Hadoop. Опишем основные моменты в работе этой системы. Giraph работает с графами. Граф — это множество вершин и множество рёбер, которые соединяют эти вершины. Графы бывают ориентированными и неориентированными. Технически Giraph поддерживает только ориентированные графы; чтобы сделать неориентированный граф, нужно создать два ребра между вершиной А и Б: от А к Б и от Б к А, с одинаковыми значениями.

Каждая вершина и каждое ребро имеют своё значение, причём значения вершин и рёбер могут быть разных типов (выбирается в зависимости от задач). Каждая вершина содержит класс, который реализует интерфейс Computation и в котором описан метод compute. Вычисления в Giraph происходят в виде суперстепов (superstep). На каждом суперстепе для вершин вызывается метод compute. Между суперстепами вершинам доставляются сообщения от других вершин, отправленные при выполнении предыдущего суперстепа. Сообщения имеют свой тип, который не обязан совпадать с типами вершин или рёбер.

Для координации вычислений существует специальный механизм — MasterCompute (мастер). По умолчанию в вычислениях используется DefaultMaster — класс, унаследованный от абстрактного класса MasterCompute. Сам по себе он достаточно бесполезен, так как не делает ничего (во многих задачах от него ничего и не требуется). К счастью, есть возможность сделать свой мастер, он должен быть унаследован от MasterCompute, и в нём должен быть реализован метод compute, который выполняется перед каждым суперстепом. Мастер позволяет выбирать класс для вершин, агрегировать некоторые данные из вершин и завершать вычисления.

Каждая вершина может находиться в двух состояниях: активном и неактивном. Если внутри compute вызывается метод voteToHalt(), то по окончании суперстепа вершина «засыпает» — становится неактивной на следующем суперстепе. Между суперстепами вершинам доставляются сообщения, отправленные другими вершинами в ходе суперстепа. Все вершины, которые не заснули на предыдущем суперстепе или получили сообщения перед следующим, являются активными и участвуют в новом суперстепе, выполняя свой метод compute. Если все вершины неактивны, то вычисления заканчиваются. По окончании суперстепа текущее состояние графа сохраняется на диск.

Обработка графа ведётся на нескольких воркерах (workers), число которых не изменяется во время выполнения. Каждый воркер последовательно обрабатывает несколько частей графа (Partition). Граф разбивается на части, которые могут меняться в процессе обработки. Всё это делается автоматически и не требует вмешательства пользователя.

Giraph использует вычислительную модель vertex-oriented, в отличие от того же GraphX. Это может быть удобно для ряда задач, так как GraphX работает с графом как с простым набором параллельных данных, не обращая внимания на его структуру. Также стоит отметить, что GraphX работает с неизменяемыми графами и требует наличие Spark«а.

1.3. RBM и Giraph

А теперь соотнесём полученные представления о Giraph и RBM. Есть вершины (нейроны), соединённые между собой рёбрами. Они разделены на две части, которые работают по очереди: видимый и скрытый слой. Один слой посылает другому сообщения (значения активации), делая его при этом активным, а сам засыпает. Слои время от времени меняют действия, которые им необходимо произвести (это работа для мастера). Как мы видим, RBM является не чем иным, как двудольным ненаправленным графом, и отлично ложится на архитектуру Giraph«а.2. Управление исполнением compute-методов, worker context
Разберёмся с тем, как координируется работа нашей реализации RBM. Во-первых, мы используем свой master, в котором на каждой итерации выбирается нужный класс для вершин. Во-вторых, реализован свой WorkerContext — класс, в котором просчитывается текущее состояние сети и из которого вершины могут получать контекст запущенного приложения. В-третьих, это параметры, передаваемые при запуске. Мастер и контекст получают значения, переданные в параметрах.

2.1. Параметры для запуска

Для начала отметим параметры, которые можно задать в нашей реализации:

maxEpochNumber — количество повторений обучения на всех данных;
maxBatchNumber — количество батчей, используемых для обучения;
maxStepInSample — количество прогонов батча с видимого слоя на скрытый и обратно;
learningRate — темп обучения;
visibleLayerSize — количество нейронов на видимом слое;
hiddenLayerSize — количество нейронов на скрытом слое;
inputPath — путь до входных файлов;
useSampling — если true, производит семплирование на скрытом слое.

2.2. Обзор деятельности мастера

Все параметры, указанные в пункте 2.1, master использует для управления процессом обучения. Рассмотрим подробнее, как это происходит.

Сначала создаётся видимый слой. Он конфигурируется классом VisibleInitialize. Далее то же самое происходит и для скрытого слоя с классом HiddenInitialize. После того как сеть создана, можно начинать обучение. Оно состоит из нескольких эпох. Эпоха, в свою очередь, — это последовательное обучение на данном наборе батчей. Таким образом, чтобы понять, как происходит весь процесс обучения, необходимо понять обучение на одном батче.

В общем случае обучение проходит по следующей схеме (схема 1):

Чтение данных видимым слоем.
Сохранение положительного значения градиента скрытым слоем.
Сохранение положительного значения градиента видимым слоем.
Вычисление значения активации скрытого слоя.
Вычисление значения активации видимого слоя.
Вычисление значения активации скрытого слоя.
Повторение шагов 5 и 6 ещё по (maxStepInSample — 3) раза.
Обновление весов исходящих рёбер видимого слоя.
Обновление весов на скрытом слое.

Стоит отметить, что значения активации считаются на всех шагах, кроме 1-го и 9-го. Всего будет выполнено (maxStepInSample + 1) * 2 шагов.

В случае, когда мы отправляем данные на скрытый слой только один раз (maxStepInSample = 1), схема несколько меняется (схема 2):

Чтение данных видимым слоем.
Сохранение положительного значения градиента скрытым слоем.
Обновление весов исходящих рёбер видимого слоя.
Обновление весов на скрытом слое.

Значения активации в этом варианте пересчитываются только на 2-м и 3-м шагах. Таким образом, у нас получилось семь классов для нейронов (вершин графа), использующихся в процессе обучения:

Название класса	Назначение	Соответствующие шаги
Из схемы 1	Из схемы 2
`VisibleNeuronZero`	Нулевой этап обучения с чтением данных, также сохраняет положительную часть градиента для смещений	1	1
`VisibleNeuronFirst`	Сохраняет положительную часть градиента в видимом слое	3	–
`VisibleNeuronLast`	Последний шаг обучения на видимом слое, считает отрицательную часть градиента и обновляет веса рёбер, выходящих из видимого слоя	8	–
`VisibleNeuronOneStep`	Комбинация классов `VisibleNeuronFirst` и `VisibleNeuronLast`, используется в случае, когда `maxStepInSample` = 1	–	3
`HiddenNeuronFirst`	Сохраняет положительное значение градиента для скрытого слоя (только для смещений `b`, градиенты весов `w` вычисляются на видимом слое)	2	2
`HiddenNeuronLast`	Обновляет веса рёбер, выходящих из скрытого слоя	9	4
`NeuronDefault`	Вызывается как на видимом слое, так и на скрытом и просто пересчитывает значения активации	4, 5, 6	–

2.3. Использование WorkerContext и хранящихся в нём параметров в нейронах

Для того чтобы в нейронах можно было использовать передаваемые параметры, был сделан свой WorkerContext, который, во-первых, передаёт информацию о размерах слоёв при инициализации, во-вторых, даёт нейронам информацию о темпе обучения, нужно ли делать семплирование и пути к данным. В этом классе независимо от мастера просчитывается, какой класс для нейронов сейчас используется.3. Обзор инициализирующих классов
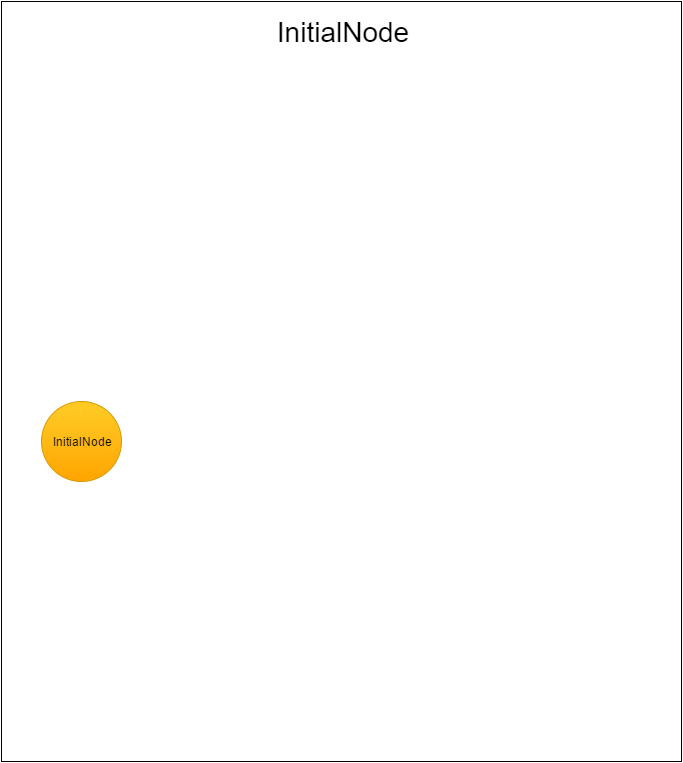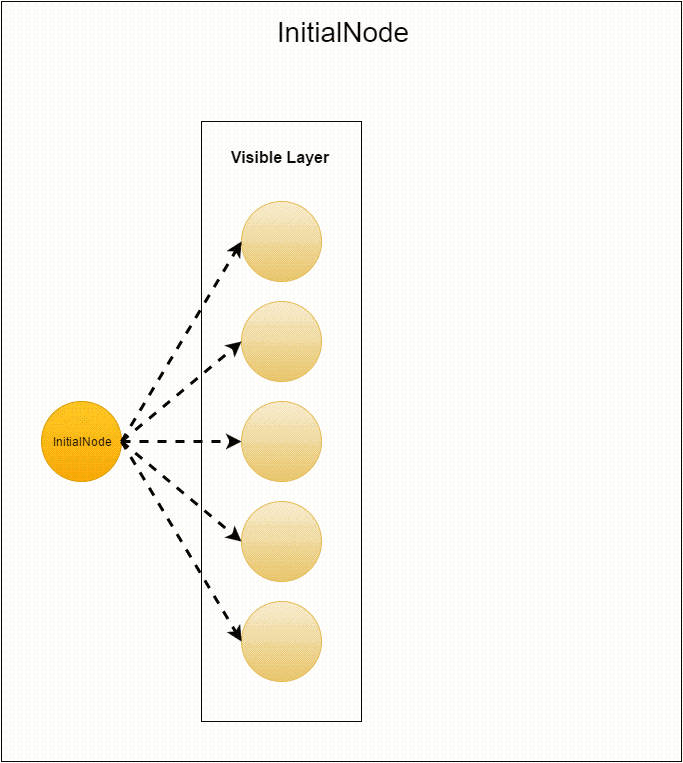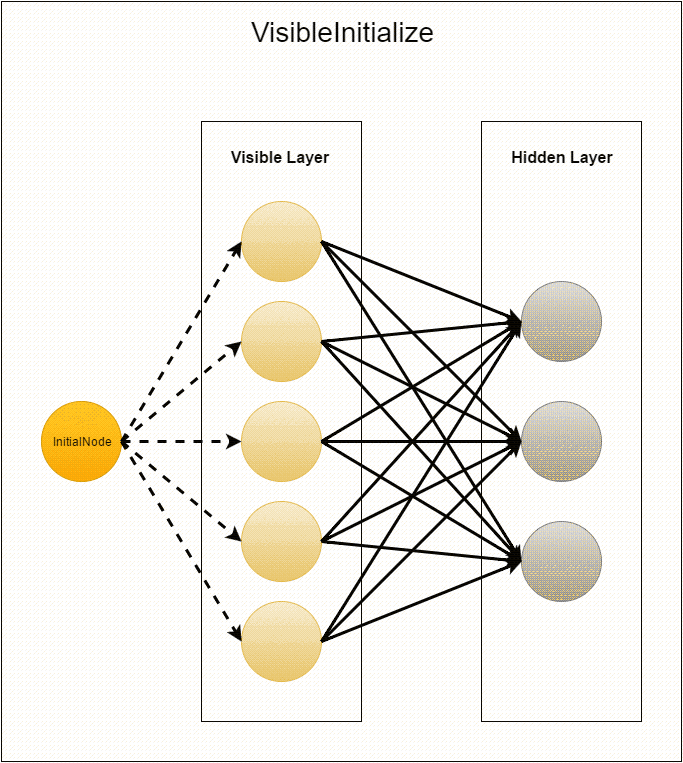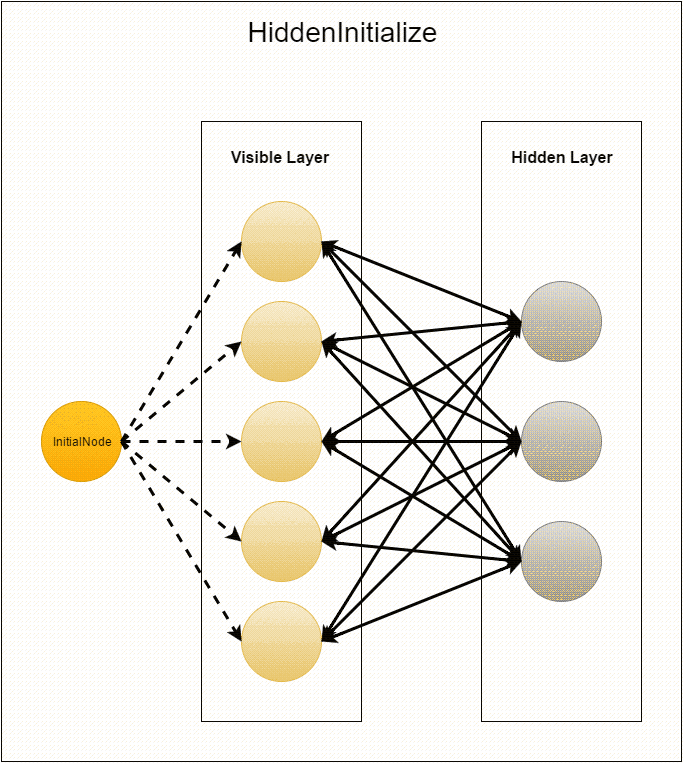
Ещё раз, но подробнее остановимся на том, как производится инициализация графа. Приложение запускается с единственной фиктивной вершиной. Она выполняет compute из InitialNode. Единственное, что происходит в этом классе, — это рассылка пустых сообщений вершинам с id от 1 до visibleLayerSize (вершины с этими идентификаторами сразу же создаются и используются уже на следующем шаге). Сразу после этого вершина «засыпает» (вызов voteToHalt) и никогда больше не используется.

Перед следующим шагом MasterCompute устанавливает VisibleInitialize в качестве compute class, таким образом, созданные в результате отправки сообщения вершины будут выполнять его. Вначале вершина генерирует выходящие из неё рёбра со случайными весами в вершины с id от –hiddenLayerSize до –1. Затем эти веса отсылаются соответствующим вершинам скрытого слоя (напомним, что это вызывает создание этих вершин). И в конце каждой вершине добавляется нулевое смещение. После этого видимый слой «засыпает», так как его создание завершено.

На последнем этапе инициализации в нейронах скрытого слоя выполняется compute из HiddenInitialize. Каждая вершина итерируется по пришедшим ей сообщениям и создаёт соответствующие рёбра. Таким образом, каждая связь между нейронами задаётся двумя рёбрами с одинаковыми весами. Далее создаются нулевые смещения. Потом скрытый слой «будит» видимый пустыми сообщениями, а сам «засыпает».

4. Описание общего класса для нейронов
Классы нейронов во многом выполняют очень похожие действия, которые можно по смыслу объединить в набор различных функций. Отличие заключается в том, что в некоторых классах вызываются / не вызываются те или иные функции. Те функции, которые вызываются во всех классах нейронов, были выделены в отдельный абстрактный класс NeuronCompute. От него унаследованы все классы нейронов, и в них реализованы функции compute, в которых могут вызываться как методы NeuronCompute, так и методы, присущие только конкретному классу. А вот, собственно, и список реализованных в нём функций:

sigma — возвращает значение сигма-функции от переданного параметра;
ComputeActivateValues — возвращает значения активации для батча в соответствии с пришедшими в сообщениях значениями активации и смещением вершины;
SendActivateValues — рассылает значения активации по исходящим рёбрам;
ComputePositivePartOfBiasGradient — возвращает положительную часть градиента для смещений;
UpdateBiases — обновляет смещение;
AddBias — добавляет в вершину нулевое смещение;
SendNewEdges — отсылает новые значения рёбер на скрытый слой.

5. Классы нейронов
Опишем классы, которые реализуют нейроны. В зависимости от номера суперстепа выбирается тот или иной класс.

5.1. VisibleNeuronZero

Данный класс выполняется первым в эпохе. Он содержит два собственных метода: ReadBatch и compute. Несложно догадаться, что в методе ReadBatch происходит загрузка очередного батча. Номер батча и путь берутся из WorkerContext«а.

/**
* Значения в вершине
*/
double[] activateValues;
double positiveBias;

activateValues = ReadBatch(vertex); // Считываем очередной батч. Номер батча и путь к файлу берутся из WorkerContext’а

positiveBias = ComputePositivePartOfBiasGradient(activateValues); // Считаем положительную часть градиента для смещений

SendActivateValues(vertex, activateValues); // Посылаем значения активации всем смежным вершинам

/**
* Обновляем значения в вершине
*/
JSONWritable value = vertex.getValue();
value.addDouble("Positive bias", positiveBias);
value.addArray("Value", activateValues);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.2. HiddenNeuronFirst

Это первый класс, выполняющийся на скрытом слое. Он полностью состоит из методов класса NeuronCompute. Взглянем на его compute:

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues;
double positiveBias;

activateValues = ComputeActivateValues(vertex, messages, bias); // Считаем значения активации

positiveBias = ComputePositivePartOfBiasGradient(activateValues); // Считаем положительную часть градиента для смещений

SendActivateValues(vertex, activateValues); // Отправляем новые значения активации

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addDouble("Positive bias", positiveBias);
value.addArray("Value", activateValues);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.3. VisibleNeuronFirst

Теперь, когда у нас есть значения активации для видимого и скрытого слоя, мы можем посчитать положительную часть градиента для рёбер.

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues = vertex.getValue().getArray("Value");
HashMap positiveGradient;

ArrayList valueAndGrad = ComputeActivateValuesAndPositivePartOfGradient(vertex, messages, activateValues, bias); // Считаем новые значения активации и положительную часть градиента
activateValues = (double[])valueAndGrad.get(0);
positiveGradient = (HashMap)valueAndGrad.get(1);

SendActivateValues(vertex, activateValues); // Отправляем значения активации

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addArray("Value", activateValues);
value.addHashMap("Positive gradient", positiveGradient);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.4. NeuronDefault

Этот класс общий для обоих слоёв. Приведём его compute:

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues;

activateValues = ComputeActivateValues(vertex, messages, bias); // Пересчитываем значения активации

SendActivateValues(vertex, activateValues); // Рассылаем значения активации

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addArray("Value", activateValues);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.5. VisibleNeuronLast

Это последний этап, выполняющийся на видимом слое, и именно в нём происходит обновление весов. На нём бы всё и закончилось (как в последовательных реализациях), но нужно также обновить рёбра, направленные в обратную сторону.

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues = vertex.getValue().getArray("Value");
double positiveBias = vertex.getValue().getDouble("Positive bias");

activateValues = ComputeGradientAndUpdateEdges(vertex, messages, activateValues.length, bias); // Вычисляем градиент и обновляем рёбра. Возвращаем значение активации

bias = UpdateBiases(activateValues, bias, positiveBias); // Обновляем смещение

SendNewEdges(vertex); // Отправляем новые веса рёбер скрытому слою

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addArray("Value", activateValues);
value.addDouble("Bias", bias);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.6. HiddenNeuronLast

На этом шаге берём новые веса рёбер из сообщений и устанавливаем их на существующие рёбра.

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues = vertex.getValue().getArray("Value");
double positiveBias = vertex.getValue().getDouble("Positive bias");

UpdateEdgesByMessages(vertex, messages); // Итерируемся по сообщениям и обновляем веса рёбер

bias = UpdateBiases(activateValues, bias, positiveBias); // Обновляем смещения

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addDouble("Bias", bias);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

5.7. VisibleNeuronOneStep

Этот класс используется в случае, когда осуществляется один проход значений активации на скрытый слой и обратно. В нём объединён функционал классов VisibleNeuronFirst и VisibleNeuronLast.

/**
 * Значения в вершине
 */
double bias = vertex.getValue().getDouble("Bias");
double[] activateValues = vertex.getValue().getArray("Value");
double positiveBias = vertex.getValue().getDouble("Positive bias");

activateValues = ComputeGradientAndUpdateEdges(vertex, messages, activateValues, bias); // Считаем положительный и отрицательный градиент и обновляем с его помощью веса рёбер

bias = UpdateBiases(activateValues, bias, positiveBias); // Обновляем смещения

SendNewEdges(vertex); // Отсылаем новые веса рёбер на скрытый слой

/**
 * Обновляем значения в вершине
 */
JSONWritable value = vertex.getValue();
value.addArray("Value", activateValues);
value.addDouble("Bias", bias);
vertex.setValue(value);

vertex.voteToHalt(); // Засыпаем

6. Описание вспомогательных классов

6.1. JSONWritable

JSONWritable — класс, используемый нами в качестве класса для значения в вершинах и для отправляемых сообщений. По сути это Writable-обёртка для JSON-объекта. Такой формат хранения данных удобен, поскольку тип и количество значений, которые нужно хранить, меняются в зависимости от текущей итерации. В качестве библиотеки для работы с JSON используется Google GSON. Для записи и отправки JSON-строка оборачивается в объект класса Text.

Для Writable-класса основными методами являются readFieds — считать объект этого класса с потока ввода и write — записать объект в поток вывода. Ниже представлена их реализация для класса JSONWritable.

public class JSONWritable implements Writable {
    private JsonElement json;

    public void write(DataOutput out) throws IOException {
        Text text = new Text(this.json.toString());
        text.write(out);
    }

    public void readFields(DataInput in) throws IOException {
        Text text = new Text();
        text.readFields(in);
        JsonParser parser = new JsonParser();
        this.json = parser.parse(text.toString());
    }

    /*
    Вспомогательные функции
    */
}

Поскольку в JSON-объекте необходимо было хранить много разных данных, удобно представлять его в виде словаря со строковыми ключами (Bias, PositiveGradient и т. д.). Для данной задачи нужно было записать в JSON некоторые сложные объекты, в том числе в вершинах необходимо хранить положительную часть градиента для рёбер. Она представляется в виде HashMap, ключами которого служат id вершин назначения рёбер (типа long), а значениями — положительная часть градиента соответствующего ребра (типа double). Для этого у JSONWritable были написаны специальные методы для добавления и извлечения HashMap по ключу.

public HashMap getHashMap(String key) {
    HashMap a = new HashMap();
    Iterator it = this.json.getAsJsonObject().getAsJsonObject(key).entrySet().iterator();
    while (it.hasNext()) {
        Map.Entry me = (Map.Entry) it.next();
        a.put(Long.valueOf(me.getKey().toString()), ((JsonElement) me.getValue()).getAsDouble());
    }
    return a;
}

public void addHashMap(String key, HashMap a) {
    Iterator it = a.entrySet().iterator();
    JsonObject obj = new JsonObject();
    while (it.hasNext()) {
        Map.Entry me = (Map.Entry) it.next();
        obj.addProperty(me.getKey().toString(), (double) me.getValue());
    }
    this.json.getAsJsonObject().add(key, obj);
}

6.2. RBMInputFormat

Этот класс используется для считывания записанного в файл графа. Он является модификацией стандартного JsonLongDoubleFloatDoubleVertexInputFormat для работы с другими типами данных. Входные данные должны быть записаны в следующем виде: каждая строка входного файла является JSON-списком, соответствующим одной вершине. Каждый список записан в формате [Id_вершины, значение_в_вершине, список_рёбер], где Id — целое число, значение — JSON-объект, список рёбер — JSON-список вида [[Id_вершины_назначения, значение_на_ребре], … ].7. Оптимизации
Многие параметры работы Giraph, такие как способ хранения рёбер и сообщений, способ разбиения вершин между воркерами, уровень дебагового вывода и настройки счётчиков, можно настраивать при запуске из командной строки. Полный список параметров запуска можно найти на http://giraph.apache.org/options.html. Настройка этих опций под конкретную задачу позволяет добиться заметного прироста в производительности.

7.1. Хранение рёбер

В Giraph рёбра по умолчанию хранятся в виде массива байтов (ByteArray) и при каждом обращении заново десериализуются. Это помогает сэкономить память, однако увеличивает время работы. Для ускорения программы мы попробовали хранить рёбра в виде списка (ArrayList) и в виде словаря, ключами в котором являются конечные вершины рёбер (HashMap). Список позволяет быстро итерироваться по рёбрам, в то время как словарь — быстро находить ребро по его вершине назначения.
Класс для хранения выходящих рёбер — один из стандартных параметров запуска Giraph, и его можно настраивать, добавив в строку запуска -ca giraph.outEdgesClass=org.apache.giraph.edge.ArrayListEdges (или другой класс).

Скорость работы тестировалась при следующей конфигурации сети: около 800 видимых нейронов, 150 скрытых, 50 воркеров, 100 объектов в батче, два шага пересчёта значений активации (maxStepInSample=2), соответственно, 6 суперстепов на каждый батч. На графике ниже представлена зависимость среднего времени работы каждого суперстепа при разных форматах хранения рёбер. Из графика видно, что на тех шагах, где происходит пересчёт значений активации, а значит, итерация по рёбрам (шаги 2—4), удаётся добиться ускорения на 20%.

7.2. Использование векторных операций

Основная работа при вычислениях значений активации и работе с ними ведётся с батчами. Поэтому для удобства можно использовать векторные операции. Это даёт небольшой прирост в производительности, так как эти функции оптимизированы для векторов. Особенно это должно быть заметно при больших размерах батчей. Мы, в свою очередь, обратили внимание на библиотеку smile, и часть операций с батчами реализована посредством этой библиотеки.

Увеличение производительности тестировалось при той же конфигурации сети, что и в предыдущем пункте. График со средним временем работы каждого суперстепа представлен ниже.

8. Дальнейшие планы
На данный момент загрузка батчей реализована самым простым образом — непосредственным считыванием из файловой системы. Такой способ работы с данными имеет ряд недостатков, поэтому мы исследуем другие способы, в частности применение Hive — хранилища данных на основе HDFS с использованием SQL-подобного синтаксиса.9. Future work
Как мы видим, Giraph — весьма многофункциональный инструмент, который может быть адаптирован под множество различных задач, в том числе и обучение RBM. В нём есть множество настраиваемых параметров, начиная от способа хранения данных и форматов ввода/вывода графа и заканчивая разбиением графа на части для хранения и количеством воркеров. С другой стороны, эффективное использование этих параметров требует понимания устройства Giraph. В статье мы попытались сделать краткий экскурс в эту область и показали несколько оптимизаций, которые могут быть использованы и в других проектах.10. Ссылки

Статья Павла Нестерова про RBM
Статья Джеффри Хинтона
Сайт Giraph«а
Smile
Claudio Martella, Roman Shaposhnik, Dionysios Logothetis. Practical Graph Analytics with Apache Giraph. 2015.
Код RBM на Giraph