Python и красивые ножки — как бы я знакомил сына с математикой и программированием
Раньше мы уже искали необычные модели Playboy с помощью библиотеки Python Scikit-learn. Теперь мы продемонстрируем некоторые возможности библиотек SymPy, SciPy, Matplotlib и Pandas на живом примере из разряда занимательных школьных задач по математике. Цель — облегчить порог вхождения при изучении Python библиотек для анализа данных.

Задача 1
Стоит девушка с изящными, натренированными, а главное, оголенными ножками. Скучает. Перед тем как демонстрировать свой (n+1)-ый уровень владения техникой пикапа, хочется получше рассмотреть ножки девушки —, а стоит ли овчинка выделки? Получше рассмотреть — это под наибольшим углом. Можно незаметно подходить к девушке (типа вдаль смотришь), но приседать нельзя — надо же как-то и приличия соблюдать. С какого расстояния ножки видны под наибольшим углом? Допустим, Ваш рост таков, что глаза находятся на высоте m над поверхностью земли. Ноги девушки оголены до высоты f.
Решение
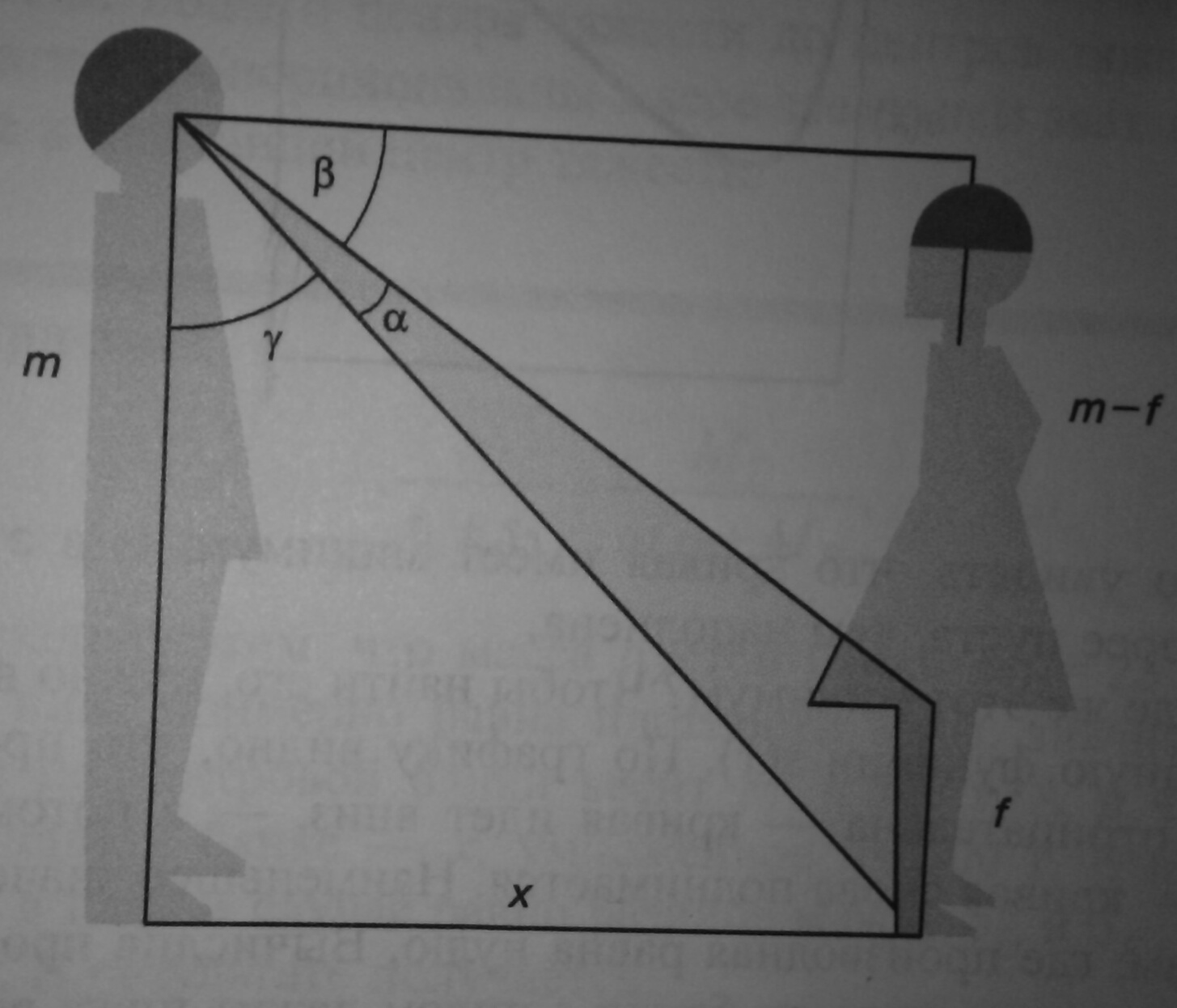
Картинка и перефразированная задача из «Кристоф Дрессер: Обольстить математикой. Числовые игры на все случаи жизни. Бином. Лаборатория знаний, 2015»
Поясним проблему. Издалека плохо рассматривать ноги — они видны под слишком малым углом. Но и если подойти слишком близко, ноги тоже будут видны под малым углом. Где-то должно быть оптимальное расстояние.
Пусть x — расстояние до девушки, f — длина оголенной части ног девушки, alpha — угол, под которым ноги видны (надо максимизировать).
Угол alpha проще всего найти, вычитая из прямого угла углы beta и gamma. Если школьная тригонометрия еще как-то жива в закоулках мозга, легко получим, что
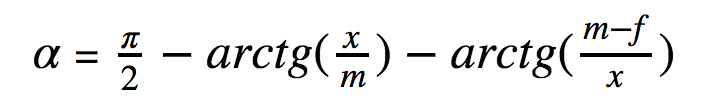
Задача сводится к максимизации alpha (x) по переменной x.
Ну это тоже просто, скажем мы: зануляем производную — и вперед!
Для начала построим график функции alpha (x). Для определенности возьмем значения пераметров m=1.7 м и f=0.7 м (хотелось бы 1 м, но все же предполагается, что имеется некая юбка.)
Теперь код. Используется сборка Anaconda и тетрадки IPython. Код воспроизводим, лежит в репозитории GitHub.
# отключим лишние предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
# магическая команда IPython, чтоб картинки прямо в тетрадке рисовались
%pylab inline
import numpy as np
from math import pi, atan
def alpha(x, m, f):
return pi/2 - atan(x/m) - atan((m-f)/x)
# задаем иксы с некоторым мелким шагом
x = np.arange(0, 6, 0.05)
plot(x, [alpha(i, 1.7, 0.7) for i in x])
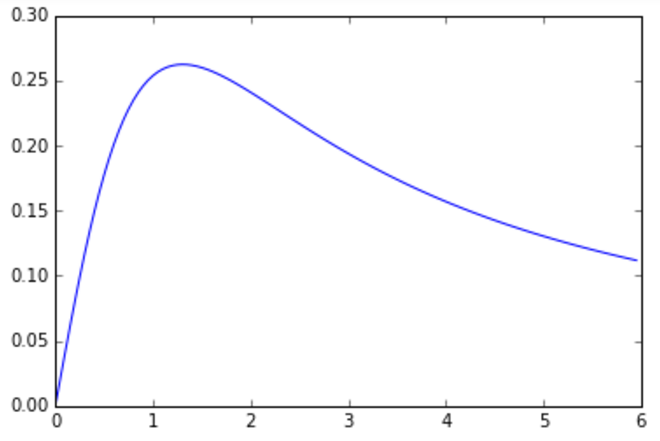
О! Предположение подтвердилось: где-то в 1–1.5 м от девушки ее ноги видны под наибольшим углом. Ну… это уже сложно без палева. Давайте теперь найдем точное значение оптимального расстояния до девушки.
Аналитическое решение «от руки»
Аналитическое решение очень простое, достаточно помнить производную арктангенса. На Хабре LaTeX не поддерживается, так что эта часть в соответствующей тетрадке IPython.
Результат получается такой:
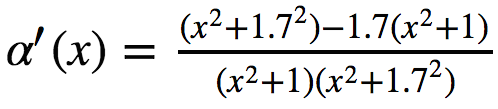
Аналитическое решение с SymPy
SymPy — это библиотека символьных вычислений на языке Python. Мы рассмотрим, как с ее помощью вычислять производные (метод diff) и находить корни уравнений (метод solve).
import sympy as sym
Заведем символьную переменную x и функцию alpha (x). Для символьных вычислений число Пи и арктангенс тоже надо взять из SymPy.
x = sym.Symbol('x')
alpha = sym.pi/2 - sym.atan(x/1.7) - sym.atan(1/x)
alpha # -atan(1/x) - atan(0.588235294117647*x) + pi/2
Посчитаем производную alpha'(x). Методу diff надо указать функцию, переменную, по которой происходит дифференцирование, и порядок производной, в данном случае 1.
alpha_deriv = sym.diff(alpha, x, 1)
alpha_deriv # -0.59/(0.35*x**2 + 1) + 1/(x**2*(1 + x**(-2)))
Можно убедиться, что это то же самое, что получалось, если взять в руки карандаш и бумагу.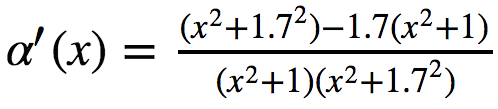
Как видно, к общему знаменателю SymPy просто так выражения не приводит. Для этого есть метод simplify.
sym.simplify(alpha_deriv) # (-0.24*x**2 + 0.41)/((0.35*x**2 + 1)*(x**2 + 1))
Теперь найдем нули производной с помощью метода solve.
sym.solve(alpha_deriv, x) # [-1.30384048104053, 1.30384048104053]
Опять получили, что лучше всего рассматривать девушку примерно с 1.3 м. Интересно, фотографы тоже такие вычисления проводят?
Численное решение c SciPy
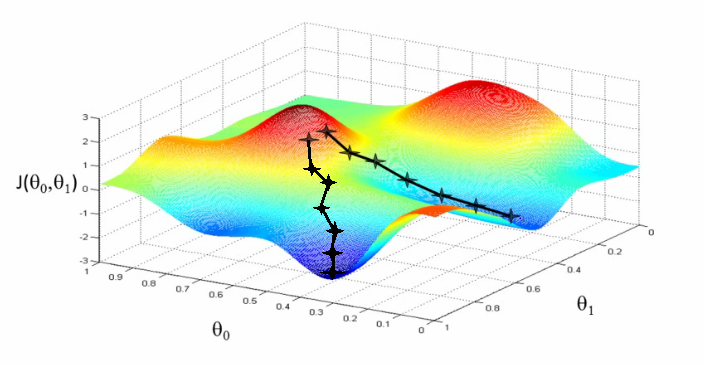
Картинка из курса Andrew Ng по машинному обучению
В библиотеке SciPy помимо всего полезного реализованы разные методы численной оптимизации. Подробное описание многих методов минимизации одномерных и многомерных функций даны в документации метода scipy.optimize.minimize.
Метода maximize как такового нет, поэтому задача максимизации будет эмулироваться минимизацией функции, домноженной на (-1). Рассмотрим самый простой случай — минимация скалярной функции одной переменной. Реализованы методы оптимизации 'brent', 'bounded' и 'golden', но отличия почему-то толком не документированы.
from scipy.optimize import minimize_scalar
alpha = lambda x: -(pi/2 - atan(x/1.7) - atan(1/x))
result = minimize_scalar(alpha, bounds=[0., 100.], method = 'bounded')
Ответ прежний, как и ожидалось.
result.x # 1.3038404104038319
Теперь выберем девушку, на чьи ноги будем любоваться. Вернемся к знакомому набору данных girls.csv по моделям месяца по Playboy. Выберем самую высокую из недистрофичных девушек. Заодно покажем кое-что из библиотеки Pandas.
Задача 2
Найти среди моделей Playboy девушку с самым высоким ростом при «нормальном» индексе массы тела — от 18 до 18.5.
Решение
import pandas as pd
girls = pd.read_csv('girls.csv') # объект Pandas.DataFrame
girls.head() # посмотреть 5 первых записей
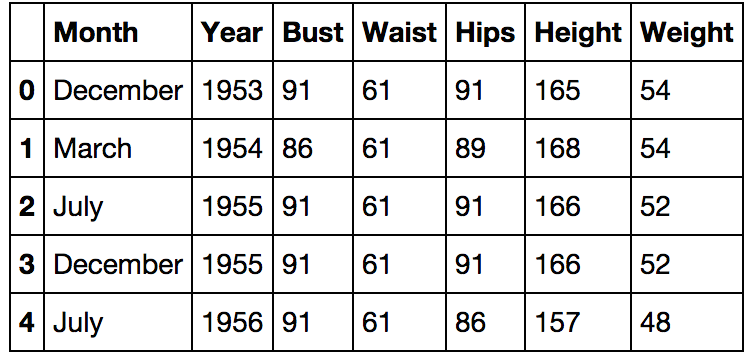
Создадим новый признак BMI — индекс массы тела, равный весу, деленному на рост в метрах в квадрате.
girls['BMI'] = 100 ** 2 * girls['Weight'] / (girls['Height'] ** 2)
Построим гистограмму распределения BMI.
girls['BMI'].hist()

Википедия говорит, что нормальный индекс BMI — 18,5—24,99. Видим, что средний индекс у моделей Playboy примерно на нижней границе нормы.
Отберем девушек с BMI от 18 до 18.5.
selected_girls = girls[(girls['BMI'] >= 18) &
(girls['BMI'] <= 18.5)]
selected_girls.sort(columns=['Height', 'Bust'],
ascending=[False, False]).head(1)
# Month Year Bust Waist Hips Height Weight BMI
#430 July 1994 91 61 91 180 59 18.209877
Это Miss July 1994 по версии Playboy Traci Adell. Дальше поисковик в помощь. Такой выбор вряд ли разочарует.
Итак, мы посмотрели самые основы использования библиотек Python SymPy, SciPy и Pandas. Обилие примеров уже реального использования этих библиотек можно найти в репозиториях GitHub. Один из обзоров таких репозиториев тут.
