«Психологика» в кубе
Не так давно проходил тест у психиатра. Хорошо, что не стал с ним спорить о том, что же куб или не куб нарисовали в тесте канадские учёные. Тест я благополучно прошёл. Но остались сомнения: чем мог для меня закончиться спор с психиатром? Ведь теперь запись врача в электронную медицинскую карту не так легко оспорить и исправить пациенту. А уж смотреть то эту электронную карту может не только пациент.
Тест у психиатра
Справка от психиатра требовалась для оформления водительских прав. Пошел пораньше в психдиспансер, народа было мало. Врач психиатр (молодая женщина) добродушно начала беседу и, тем не менее, далее в непринуждённой беседе прошлась по всем моим датам (выяснила: помню ли их я). Затем предложила мне листочек с заданиями теста.
Первое задание: соединить прямыми возрастающие числа, хаотично расположенные на листочке. Задание мне понравилось — получился красивый полигон. Он придал мне математический настрой. С ним я приступил ко второму заданию.
Врач показала листочек (с рисунком 1) и сказала: — Здесь нарисован куб, и вам тоже следует нарисовать куб.

Рисунок 1. Куб, нарисованный в тестах.
Я рассуждал: стороны квадрата с рисунка 1 параллельны обрезам листа, значит рёбра, исходящие из его углов, перпендикулярны плоскости листа с рисунком. Каждое из них должно проецироваться в точку. И тут математика дёрнула меня за язык, и у меня вырвалось:
— Вообще-то, здесь нарисован не куб!
Возникла пауза.
Конечно, мне было понятно, что это кабинетная проекция — косоугольная проекция, которую только условно можно считать реалистичным рисунком. Но тут мне вспомнились кадры из одной старой комедии про рационального математика.
Этот математик, объезжая закоулками пробки, на своём микро-авто, подтолкнул слона, которого переводили по дороге из зоопарка. Слон присел и помял капот авто. Полицейским, остановившим помятое авто, не понравился ответ математика:
— Это слон сел мне на капот. Математика отправили в психлечебницу. «Старожил» психушки поучал математика: — Если хочешь отсюда выйти, то сразу не говори доктору, что слон был всего один. Сначала скажи — три слона, потом — два, пока все слоны не кончатся, и доктор поймет, что он тебя вылечил.
Врач прервала паузу и спросила: — А вы специалист?
— Вообще-то, я в этом разбираюсь, но не буду тратить время, — ответил я и нарисовал куб, а для пущей наглядности пунктиром обозначил невидимые рёбра.
В следующем задании: «показать стрелками часов время без четверти восемь», я не стал умничать, нарисовал стрелки. Врач одобрительно кивнула.
Остальные задания вопросов и сомнений не вызвали. В последнем задании: «Подобрать обобщенное имя к предметам, нарисованным на карточке», например, для мотоцикла и велосипеда — транспортные средства, тоже трудностей не возникало. А когда появилась карточка с ботинком и карандашом, я не стал придумывать «атрибуты дизайнера обуви» или умничать, что эти предметы надо задавать как «перечисляемое множество», а вопросительно посмотрел на врача.
Она сказала: — Если затрудняетесь, ставьте прочерк.
Так я и сделал. На этом тест закончился. Мне выдали справку с положительным заключением.
Домашняя проработка
Вновь я вспомнил про этот куб, когда случайно увидел его на 1-ом ТВ-канале центрального телевидения в передаче Е.В. Малышевой про здоровье. Оказалось, что тест с этим кубом специально разработали канадские учёные. Ну, раз здесь постарались канадские учёные, то отвечу цитатой из [1]:»– Учёностью меня не обморочишь!…»). Ведь ни в проектировании, ни в реалистическом рисовании не применяют кабинетную проекцию, а практически используют прямоугольное и центральное (перспективное) проецирование. И если считать, что используется общепринятое прямоугольное проецирование, то, напрашивается вопрос: что же за фигура была изображена? И сама собой возникла геометрическая задачка №1.
Задачка №1.
Фронтальная (прямоугольная) проекция шестигранника выглядит (см. рисунок 1) как кабинетная проекция куба. Считая, что грани, параллельные фронтальной плоскости, — квадраты, а расстояние между ними равно длине стороны этих квадратов, построить вертикальную и профильную проекции шестигранника. Также определить его тип и угол наклона рёбер к фронтальной плоскости (то есть угол между ребром и его проекцией на плоскость квадрата).
А для тренинга к заданиям 2 и 3 подготовил задачку №2 и задачку №3.

Рисунок 2. «Претенденты» на изображение куба.
Задачка 2.
На каком из рисунков 2а, 2.б, 2.в, 2.г, 2.д, 2.е, 2.ж, 2.з изображён куб?
Задачка 3.
Показать стрелками часов время: «без четверти восемь».
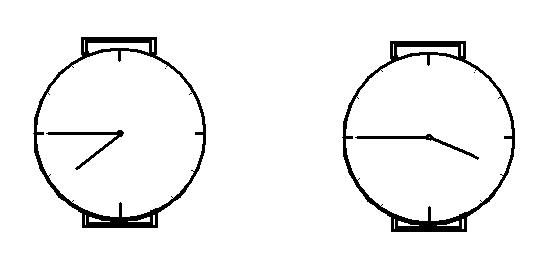
Рисунок 3. Какие часы правильно показывают время: «без четверти восемь?»
Ответы на эти навеянные тестированием задачки приведу в конце текста, а далее рискну сформулировать некоторые выводы.
Мои скромные выводы
Из моего прохождения тестирования у психиатра мне показалось, что не всегда главное точно отвечать на вопросы. Важно следовать общепринятому контексту.
Если вопрос сформулирован четко и однозначно, то ответить на него легко. Например, я встречал в тестах на IQ вопрос-задачку: «Собралась компания из 12 человек, и каждый каждому пожал руку. Сколько всего было рукопожатий?». Здесь всё просто: первый пожал 11 рук, второй — 10, …, 11-ый — одну. Всего 11+10+…+2+1=(11+1)+(10+2)+…+(5+7)+6=12×5+6=66 рукопожатий. Но не во всех вопросах чётко оговорены условия (см. ответ задачки №2), которые предполагаются по умолчанию, и даже правильный обоснованный ответ может не оказаться верным с точки зрения психиатра. Возможно, что эти вопросы специально так составляются. И уж конечно не следует спорить с психиатром. Важно то, что врач (в ограниченное регламентом время приёма) запишет в вашу медицинскую карту. Ведь это может иметь серьёзные последствия. И не так легко пациенту оспорить и исправить негативную запись. А уж смотреть то эту электронную карту может не только пациент. Конечно, полезно знать об этом мнение специалистов и учитывать их рекомендации.
Ответы к задачкам и способ построения решений
При геометрических построениях, доказывающих правильность альтернативной точки зрения, необходимо обеспечить высокую точность. Её требовали даже при традиционных графических построениях. Рассказывают, что классик отечественной начертательной геометрии профессор Владимир Осипович Гордон [2] на экзамене сделал замечание студенту, который не чертил, а рисовал всё от руки. Студент огрызнулся: — А какая разница? Профессор сказал: — Это начертательная геометрия! И вообще, кто кого учит: яйца курицу или курица яйца? Студент: — Вообще-то, курица учит. Профессор: — То-то! А я старая курица! Студент и с этим согласился, взял линейку и стал чертить, а не рисовать.
Но здесь используем не графическое, а математическое задание координат вершин шестигранника и компьютерные вычисления координат их проекций на плоскость проецирования. Так что погрешность обуславливается только разрешением при графическом выводе.
Ответ к задачке 1.
Тип шестигранника: наклонная призма с основаниями — квадратами (эти грани по определению лежат в параллельных плоскостях). Боковые грани призмы — параллелограммы, две стороны каждого параллелограмма — рёбра, совпадающие со сторонами квадратов, лежащих в основании призмы, а два других ребра наклонены под углом π/2 — arccos (2/√5)≈63,435° к основаниям призмы.

Рисунок 4. Изображение наклонной призмы («кабинетного куба»).

Рисунок 5. Чертёж наклонной призмы (к задачке 1).
Ответ к задачке 2.
Все 8 изображений, показанных на рисунке 6, являются правильными аксонометрическими изображениями куба. Этот куб (с единичной длиной рёбер) размещён в первом квадранте так, что три его ребра совмещены с координатными осями прямоугольной системы координат. На рисунке 6 для перспективных (центральных) проекций указаны: O — начало uOv-координат на картинной плоскости, G — центр пучка. Взгляд наблюдателя направлен из точки G к точке O перпендикулярно картинной плоскости. А какой рисунок окажется верным на взгляд психиатра? И хотя все изображения правильные, в тесте я нарисовал куб, как на рисунке 6.д.

Рисунок 6. Изображения куба в параллельных и перспективных проекциях.
Ответ к задачке 3.
Если внимательно посмотреть на рисунок 7 и включить логическое мышление, то уверенно можно сказать, что именно часы справа показывают время «без четверти восемь». А вот часы слева могут показывать ещё и время »19 часов 45 минут». Вроде бы всё логично. А какой вариант подойдёт для ответа психиатру? В тесте я не стал искушать судьбу (использовал иную «логику») и нарисовал стрелки как у часов, показанных слева.

Рисунок 7. Часы, которые должны показывать время «без четверти восемь».
Справочные материалы
Основные определения
Аксонометрия (аксонометрическая проекция) — проекция фигуры (с пространственной системой координат) на некоторую (картинную) плоскость.
Картинная плоскость — плоскость, на которую проецируются заданные в пространственной системе координат точки фигуры.
Центральное (перспективное) проецирование – проецирование пучком прямых, исходящих из одной точки — центра пучка.
Параллельное проецирование — проецирование линиями, параллельными одному заданному направлению.
Прямоугольная проекция — аксонометрическая проекция, для которой направление проецирования перпендикулярно картинной плоскости.
Фронтальная проекция (на плоскость V) — вид спереди (простыми словами).
Горизонтальная проекция (на плоскость H) — вид сверху (простыми словами).
Профильная проекция (на плоскость W) — вид сбоку (простыми словами).
Косоугольная проекция — аксонометрическая проекция, для которой направление проецирования не перпендикулярно картинной плоскости.
Кабинетная проекция — косоугольная проекция, у которой ось x — расположена горизонтально, ось z — проведена вертикально, а ось y — проведена под углом 45° к горизонту. При построении изображений по осям x и z откладываются натуральные размеры, а по оси y — размеры сокращают в 2 раза (см. рисунок 8).

Рисунок 8. Кабинетная проекция.
Литература
[1] А.С. Грибоедов, Горе от ума, М., 1833.
[2] И.О. Гордон, М.А. Семенцов-Оргиевский, Курс начертательной геометрии, Наука, 1968.
