Проверка гипотезы равенства средних при неравной дисперсии в R11.05.2021 09:32

(при условии нормальности распределения)

Задача определения равенства средних при условии равных дисперсий — классическая задача математической статистики, которую решают в техникумах и ВУЗах. Однако МС как наука очень похожа на болото — при попытке спрыгнуть в сторону с кочки классически решаемой задачи можно увязнуть или вовсе утонуть

Рассматриваемая задача — одна из таких. На самом деле, заботливыми математиками уже разработано порядка двух десятков разных статистических тестов для решения такого рода задач, что ставит вопрос из разряда «какой из них применять»

Проведенное предварительное исследование (текст исследования доступен на GitHub) показало, что в зависимости от конкретной комбинации значений средних, дисперсии, и особенностей постановки задачи лучшим может быть чуть ли не любой из тестов, рассмотренных в статье «Cavus, M., Yazici, B. Testing the equality of normal distributed and independent groups' means under unequal variances by doex package / The R Journal. 2020. № 2 (12). P. 134–155».

Для решения этой задачи была разработана процедура, позволяющая для каждого конкретного случая определить лучший статистический тест. Она будет продемонстрирована на примере базы данных GrowthDJ, содержащих данные об экономическом росте. Проверим предположение о равенстве средних значений экономического роста (переменная gdpgrowth) в зависимости от наличия в странах качественных данных (переменная inter)

Первые этапы исследования — проверка нормальности распределений и нахождение описательных статистик:

library("tibble")

library("AER")

library("WRS2")

library("doex")

data("GrowthDJ")

XX<-na.omit(GrowthDJ)

library("psych")

describeBy(XX$gdpgrowth, XX$inter)

shapiro.test(XX[XX$inter=='yes',6])

shapiro.test(XX[XX$inter=='no',6])

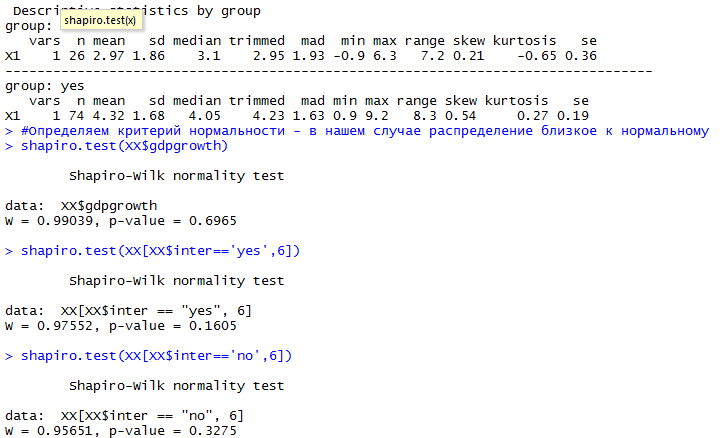
3c36e4edb45f77b7c6ebbff0cbde0a01.png

Получаем, что наши данные распределены нормальны — значит, тесты можно применять

Методика проверки

  1. Задается два средних значения и два значения дисперсии (исходя из имеющихся данных по группам)

  2. При заданных средних значениях и заданных дисперсиях генерируется три нормально распределенных выборки (каждая из 70 наблюдений). Первая — со средним значением № 1 и дисперсии № 1, вторая — со средним значением № 1 и дисперсией № 2, третья — со средним значением № 2 и дисперсией № 2.

  3. Далее с использованием выбранного теста по объединенным данным первой и третьей выборки проверяется гипотеза о равенстве средних на уровне значимости в 0.01. Если полученное p-значение критерия больше 0.01, то гипотеза отклоняется верно, если меньше 0.01 — то гипотеза ошибочно принята. По объединенным данным первой и второй выборки также проверяется данная гипотеза. Если полученное p-значение критерия меньше 0.01, то гипотеза принимается верно, если больше 0.01 — то гипотеза ошибочно отклонена. После этого данная симуляция проводится 100 раз по каждому тесту, и подводится количество разных исходов.

На основании полученных результатов выявляются лучшие тесты по следующим метрикам качества (рассчитаны по аналогии с соответствующими показателями, используемыми при анализе качества классификации):

  • accuracy (процент правильно сделанных выводов);

  • selectivity (доля правильных выводов для выборок, в которых средние не равны);

  • precision (доля правильно сделанных выводов о равенстве средних);

  • recall (доля правильных выводов для выборок, в которых средние равны);

  • FOR (доля ошибочно сделанных выводов о неравенстве средних);

  • F-мера (гармоническое среднее precision и recall, общая характеристика точности качества).

Результаты расчетов (код представлен в файле Итого.R на гитхабе) позволили получить следующую таблицу

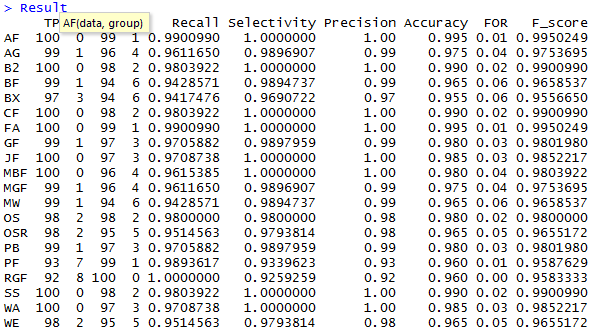
2406991f19f700a6f998165e6ab8c3af.png

Выведем лучшие тесты

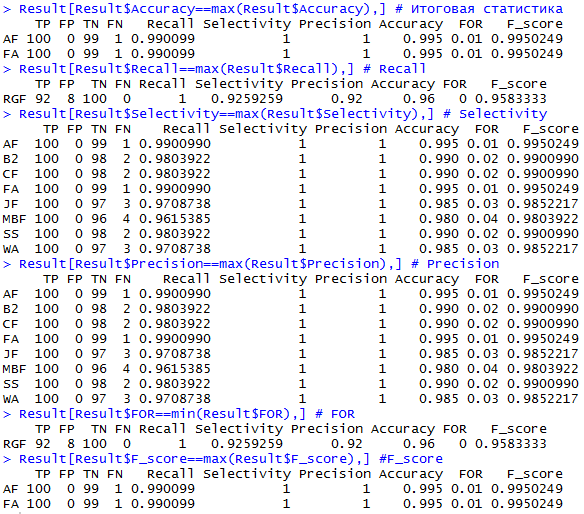
cd7d08a49b20f122b64b23fc6a4dfb10.png

Таким образом, получаем:

  • если нам нужен самый точный тест вообще, то необходимо использовать AF или FA-тест (они лучшие и по точности, и по значению F-score

  • если необходимо максимально избегать ложно-отрицательного вывода (т.е. ложного вывода о наличии различий в средних), необходимо применять RGF-тест

  • если необходимо максимально избегать ложно-положительного вывода (т.е. ложного вывода о равенстве средних), можно выбрать любой из 8 тестов (AF, BA, CF, FA, JF, MBF, SS, WA)

  • если нам нужна максимальная точность вывода о равенстве средних, то также можно выбрать любой из 8 тестов

  • если нам нужна максимальная точность вывода о неравенстве средних, то также необходимо применять RGF-тест

Итого — давайте применим AF-тест (Approximate F-test)

8af4a86b936dbccee4ca1f7ea8ed571e.png

Гипотеза о равенстве средних принята на уровне значимости 0.0003 или в терминах поставленной задачи — среднее значение темпов экономического роста не отличается в странах с наличием или отсутствием более качественных данных

© Habrahabr.ru