Прокачиваем разметку мультимодальных данных: меньше асессоров, больше слоёв18.08.2020 20:02

Всем привет! Мы — учёные лаборатории «Машинное обучение» ИТМО и команда Core ML ВКонтакте — проводим совместные исследования. Одна из важных задач VK заключается в автоматической классификации постов: она необходима не только чтобы формировать тематические ленты, но и определять нежелательный контент. Для такой обработки записей привлекаются асессоры. При этом стоимость их работы можно значительно снизить с помощью такой парадигмы machine learning, как активное обучение.

Именно о его применении для классификации мультимодальных данных и пойдёт речь в этой статье. Мы расскажем про общие принципы и методы активного обучения, особенности их применения к задаче, а также инсайты, полученные в ходе исследования.

Введение

Активное обучение — это раздел machine learning, где модель взаимодействует с учителем. Она запрашивает у него для тренировки лишь те данные, которые позволят обучиться лучше и, следовательно, быстрее.

Это направление интересно компаниям, которые привлекают асессоров для разметки данных (например, с помощью сервисов Amazon Mechanical Turk, Яндекс.Толока) и хотят удешевить этот процесс. Один из вариантов — использовать reCAPTCHA, где пользователь должен отмечать снимки, скажем, со светофорами, — и заодно получать бесплатную разметку для Google Street View. Другой способ — применять активное обучение.

Некоторые уже сейчас используют его для оптимизации краудсорсинга и делятся опытом. Например, Voyage — компания, которая занимается автопилотируемыми автомобилями. В статье её специалисты рассказали, как активное обучение позволило им не только сэкономить на разметке данных, но и повысить предельную точность модели. Их подход к активному обучению очень похож на тот, о котором расскажем мы.

Компания Amazon в своей работе описывает фреймворк DALC (Deep Active Learning from targeted Crowds). Он раскрывает концепцию активного обучения с точки зрения нейронных сетей, байесовского подхода и краудсорсинга. В исследовании в том числе используется техника Monte Carlo Dropout (о ней мы тоже поговорим в этой статье). Ещё авторы вводят любопытное понятие — noisy annotation. Если в большинстве работ по активному обучению предполагается, что асессор «говорит правду и ничего, кроме правды», то здесь допускается вероятность ошибки в силу человеческого фактора.

Про ещё одно исследование от Amazon можно прочитать здесь. В нём рассматривается концепция иерархической разметки: когда асессор вместо классической одноклассовой разметки объекта должен дать бинарный ответ о его принадлежности к определённому надклассу/классу в иерархии. При этом бинарные вопросы, как и объект для разметки, выбирает сам алгоритм. Таким образом, конечная разметка может получиться неполной: будет определён не конечный класс объекта, а его категория. Однако этого будет достаточно для обучения.

Но хватит говорить про использование парадигмы — пора рассмотреть активное обучение в деталях! У него есть несколько основных подходов, или сценариев. В нашем исследовании модель взаимодействовала с учителем по сценарию pool-based sampling.

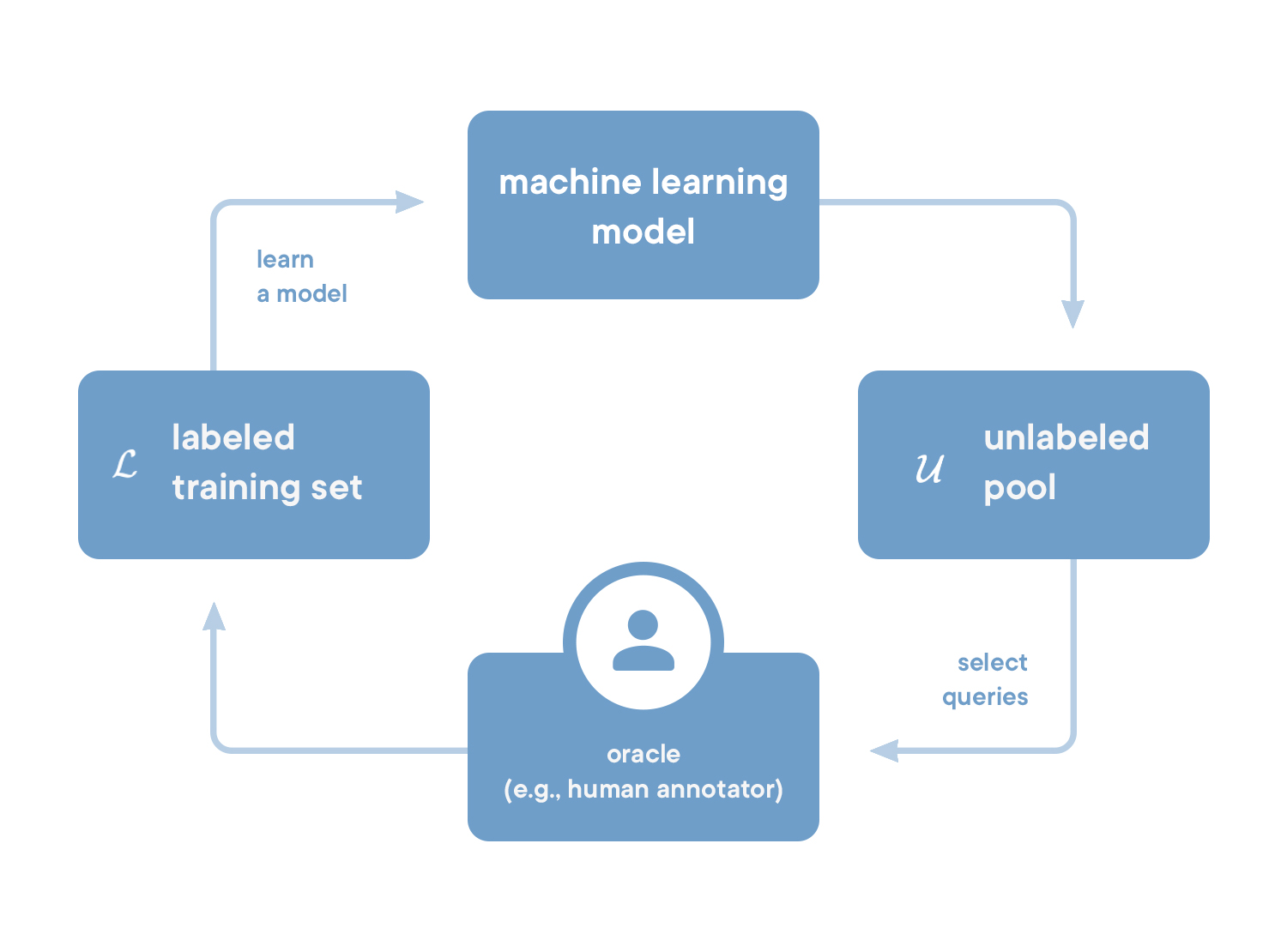
Рис. 1. Общая схема pool-based сценария активного обучения

Поясним суть этого сценария. Допустим, есть некоторое количество размеченных данных, на которых модель уже обучена (то есть прошла пассивную фазу обучения). Далее с её помощью уже можно оценивать неразмеченные данные: определять, насколько они пригодятся для дальнейшего обучения.

Наиболее полезные данные отправляются на разметку эксперту, чтобы затем вернуться для дообучения модели — уже в активной фазе. Отправленные на разметку данные называют запросом (англ. — query). Запрос может состоять как из одного объекта, так и из нескольких. Способы выбора объектов пула для запроса к эксперту (иными словами, способы оценить полезность данных) называются стратегиями активного обучения.

Далее опишем, как устроена решаемая задача и набор данных, и рассмотрим конкретные стратегии активного обучения на примере.

Набор данных и задача

Напомним, общая задача — классификация постов ВКонтакте. Они представляют собой мультимодальные данные (изображение и текст). Предоставленный набор данных включает ≈250 тыс. готовых эмбеддингов постов. Здесь каждый объект (пост) размечен одним из 50 классов — тематик публикаций — и опционально содержит:

векторное представление, или эмбеддинг (англ. embedding), картинки поста;
векторное представление текста.

Стоит отметить, что набор данных сильно несбалансирован (см. рис. 2).

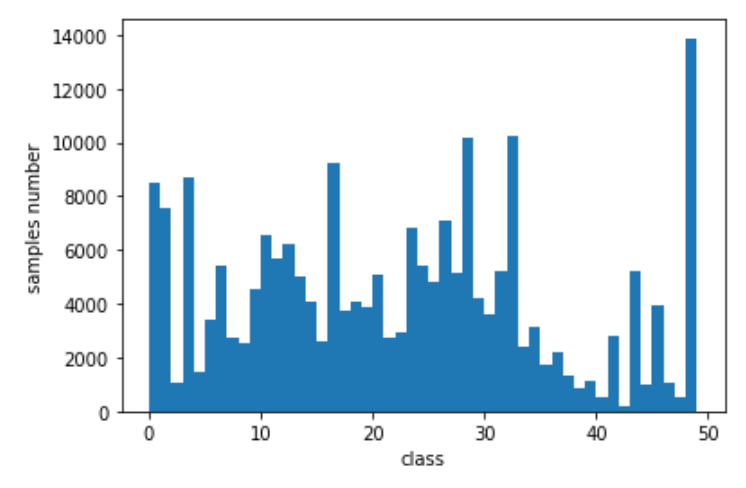
Рис. 2 — гистограмма распределения классов

Модель для классификации

Важный этап в решении любой задачи ML и активного обучения в частности — выбор оптимальной базовой модели. То есть той, на основе которой будет сравниваться активное обучение с пассивным.

Одним из ключевых требований к модели было отсутствие переобучения. Дело в том, что активное обучение подразумевает постоянное дообучение модели. А если она будет переобучена, то, как бы мы ни выбирали новые данные, точность не возрастёт значительно или вовсе будет уменьшаться. Конечно, можно было бы на каждом шаге активной фазы обучать модель с нуля, останавливая процесс с помощью early stopping. Но это сделает эксперименты слишком долгими, так как вместо одной эпохи дообучения на новых данных потребуется несколько десятков.

В проекте мы экспериментально изучили различные конфигурации глубоких нейронных сетей. Проводились эксперименты с добавлением residual соединений, highway блоков, использованием энкодеров (англ. encoder). Рассмотрели разные варианты, учитывающие мультимодальность на основе слияния (англ. fusion): метод внимания для мультимодальных данных, матричное слияние.
Но некоторые способы учёта мультимодальности данных невозможно было применить к нашей задаче — например, выравнивание и обучение различным представлениям. Это связано с готовым представлением данных в виде предобученных векторов-эмбеддингов.

Впрочем, предмет этой статьи — не классификация мультимодальных данных как таковых, а активное обучение. Так что не будем подробно останавливаться на выборе базовой модели, а опишем лишь конечную.

Критерием для выбора итоговой модели стала максимизация значения метрики валидационной точности. Итак, в качестве классификатора была подобрана следующая архитектура (рис. 3):

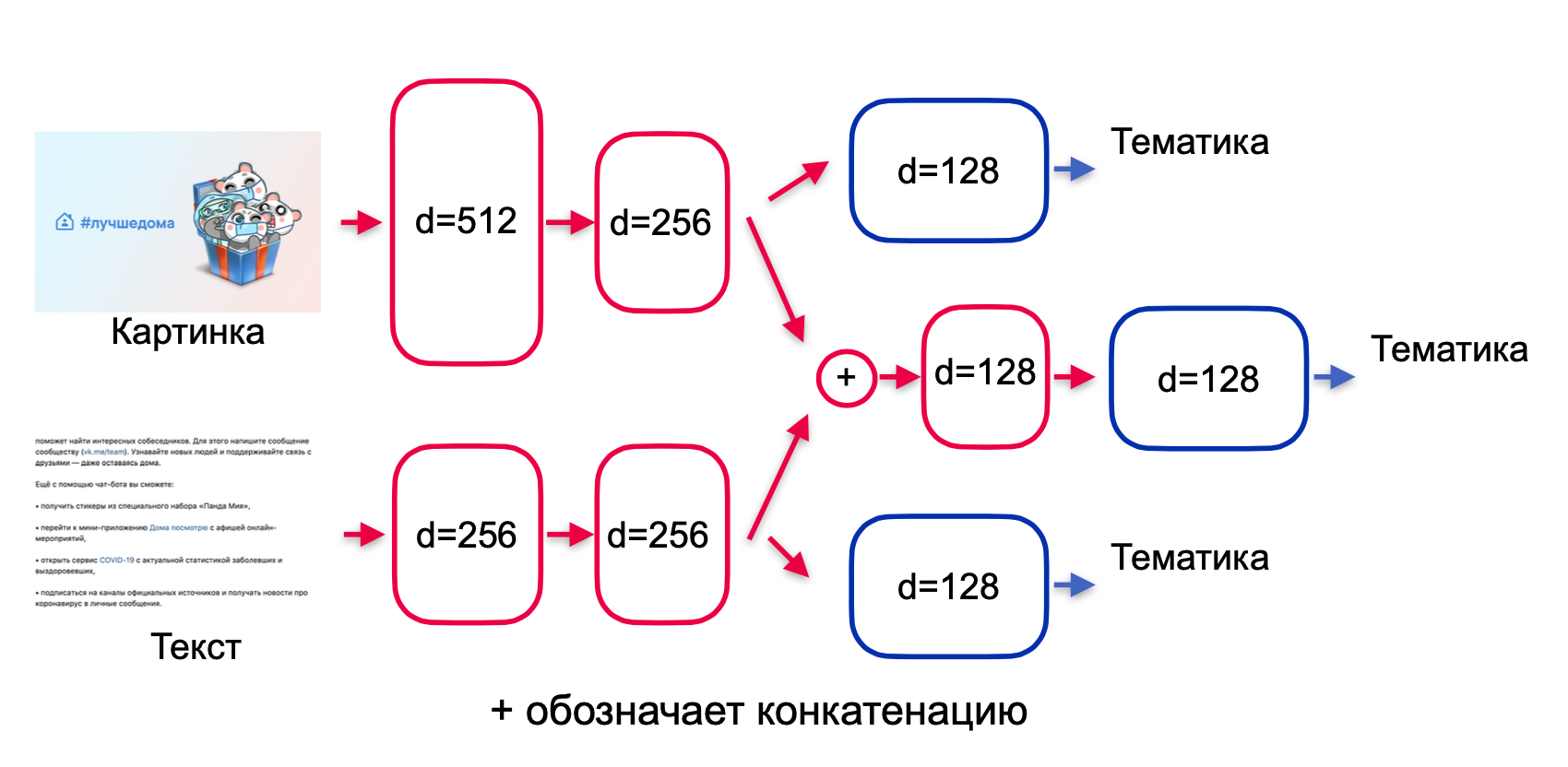
Рис. 3. Подобранная архитектура для классификации

В данной модели производится позднее слияние модальностей. Идея в том, что эмбеддинги картинки и текста сначала обрабатываются по отдельности. Такой подход позволяет уменьшить размер нейронной сети, которая сперва извлекает из каждой модальности необходимую информацию, а потом объединяет их для финального предсказания. Кроме того, три головы модели (отдельно на текст и картинку + объединённая) дополнительно стимулируют сеть обучать веса — чтобы извлекать как можно больше релевантной информации для классификации по каждой из модальностей.

Блоки, обозначенные красным и синим на рис. 3, имеют следующий вид:

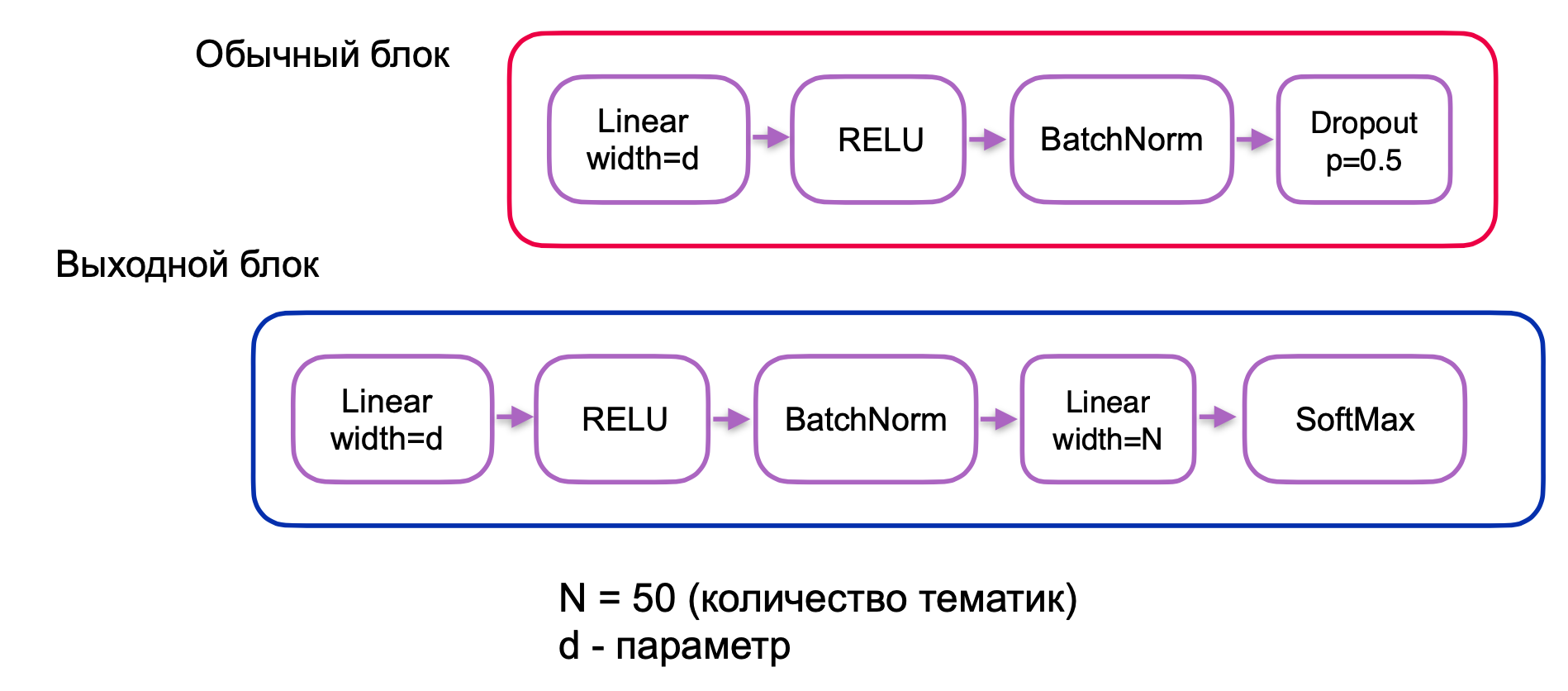
Рис. 4. Описание основных блоков модели нейронной сети для классификации

Любопытно то, что изначально разрабатывалась модель с одним выходом, а дополнительные планировалось использовать для различных стратегий активного обучения. Но оказалось, что подобранная архитектура показывает бóльшую точность, чем аналогичная модель с одним выходом, объединённым по двум модальностям.

Один из закономерных и важных вопросов, которые возникли при построении этой архитектуры: как считать функцию потерь? Варианты:

простое покомпонентное суммирование элементов функции потерь с разных голов;
взвешенная функция потерь с ручным перебором весов;
взвешенная функция потерь с обученными весами голов.

Мы выбрали третий вариант. Ещё вдохновились статьёй из области байесовского глубокого обучения: в ней комбинации функций потерь выводятся исходя из формулы maximum likelihood и учёта неопределённости предсказаний, возникающих из-за шума в данных. В итоге мы остановились на такой функции потерь:

$L = \frac{1}{\sigma_1 ^ 2}L_1 + \frac{1}{\sigma_2 ^ 2}L_2 + \frac{1}{\sigma_3 ^ 2}L_3 + \log{\sigma_1} + \log{\sigma_2} + \log{\sigma_3}$

где $L_1, L_2, L_3$ — функции потерь для разных выходов модели (в нашем случае они представляют собой категориальную кросс-энтропию), а $\sigma_1, \sigma_2, \sigma_3$ — настраиваемые параметры, характеризующие дисперсию и шум в данных.

Pool-based sampling

С моделью определились — теперь опишем, как будем применять и тестировать различные стратегии активного обучения. Согласно сценарию pool-based sampling мы составили пайплайн экспериментов:

Берём из тренировочного набора данных какое-то количество случайных объектов.
Обучаем на них модель.
Выбираем новую пачку данных из оставшегося тренировочного набора, основываясь на тестируемой стратегии, и добавляем их к размеченным данным.
Дообучаем модель.
Считаем метрики (валидационную точность).
Повторяем шаги 3–5 до выполнения определённого критерия (например, пока не кончится весь тренировочный набор данных).

Первые два шага соответствуют пассивной фазе обучения, шаги 3–6 — активной.

Помимо самой стратегии, в данном пайплайне значимыми являются два параметра, а именно:

Размер изначального набора данных, на котором обучается модель во время пассивной фазы. Если этот параметр окажется недостаточным, то сложно будет сравнить эффект от активного обучения и дообучения на случайных данных: точность будет стремительно расти в обоих случаях. Если же, напротив, сделать начальный размеченный набор слишком большим, то модель будет хорошо обучена уже в пассивной фазе. Тогда в активной рост точности будет слабым вне зависимости от метода обучения. В нашем случае оптимальным оказался размер изначального набора данных, равный 2 000.
Размер запроса к эксперту. С одной стороны, можно отправлять объекты к эксперту по одному. В этом случае первый объект в запросе будет максимизировать критерий рассматриваемой стратегии активного обучения (при сортировке объектов по убыванию соответствия критерию). И после обучения на этом объекте остальные в запросе, скорее всего, перестанут представлять интерес. Но если выбирать объекты по одному, то эксперимент затянется и всё исследование усложнится. Поэтому мы остановились на 20 объектах в запросе.
Ещё можно варьировать количество шагов в фазе активного обучения. Очевидно, что с его увеличением точность модели может расти. Но цель нашего проекта — не достичь максимальной возможной точности классификации, а исследовать эффективность активного обучения. Поэтому мы решили зафиксировать количество шагов на 100 или 200.

Теперь, когда мы определились, как и на чём тестировать методы активного обучения, перейдём к их реализации.

Инсайт №1: влияние выбора batch size

В качестве baseline рассмотрим, как обучается модель при случайном выборе данных (будем называть это пассивным обучением) (рис. 5).

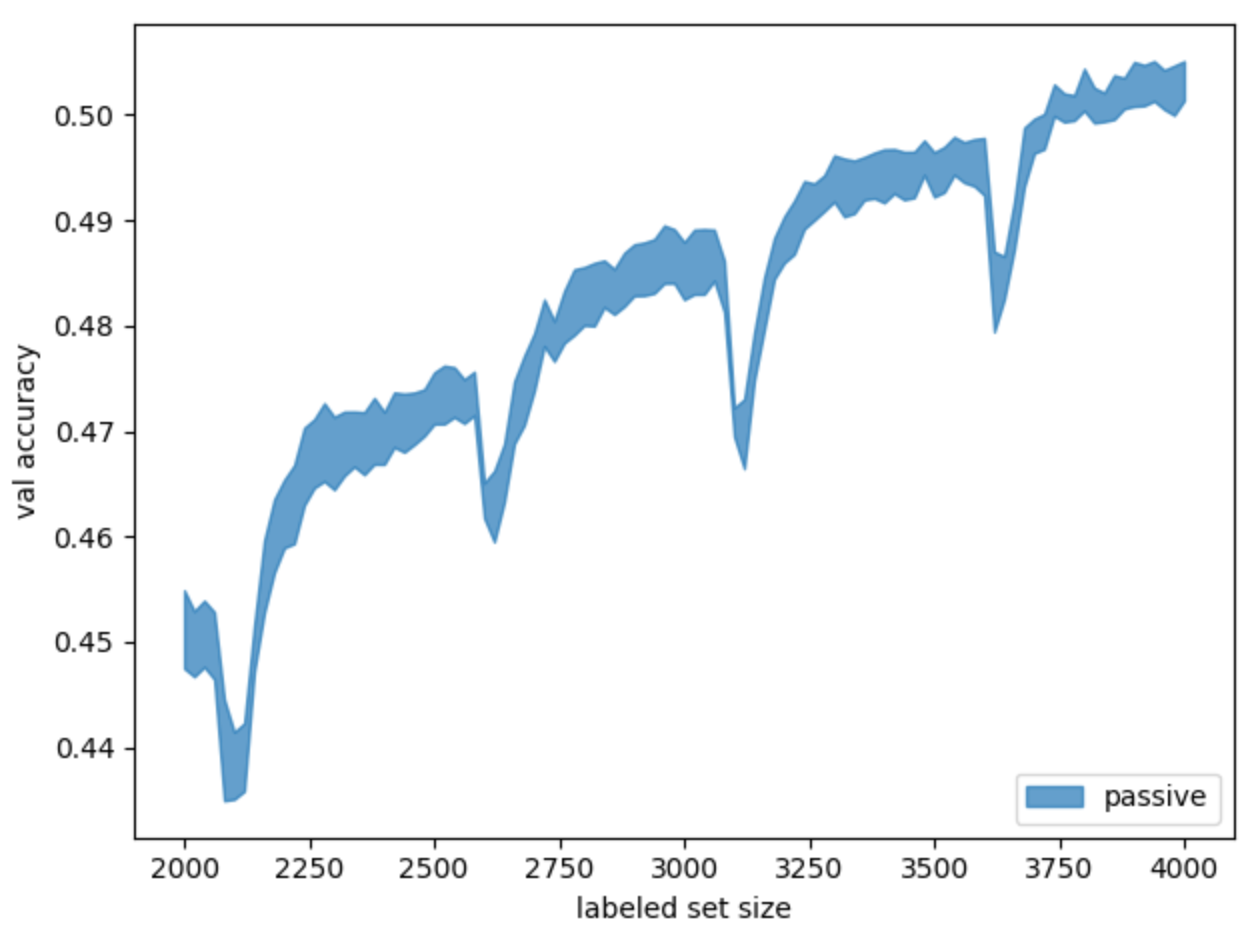
Рис. 5. График обучения baseline-модели пассивным способом. Приведён результат пяти запусков с доверительным интервалом

Для достоверности этот и все последующие эксперименты запускались по пять раз с разным random state. На графиках выводится средняя точность запусков с доверительным интервалом.

Здесь мы встретились с первым инсайтом решаемой задачи. На графике обучения с определённым периодом появляются «просадки» точности, хотя интуитивно кажется, что точность должна монотонно расти.

Чтобы устранить этот эффект, нужно осознать важность параметра размера батча (англ. batch size). В нашем случае он был по дефолту выбран равным 512 — из-за большого количества классов (50). Получалось, что при конечном размере размеченного набора данных и фиксированном batch size последний батч мог оказаться крайне мал. Это вносило шум в значение градиента и негативно сказывалось на обучении модели в целом. Мы опробовали следующие варианты решения этой проблемы:

upsample, чтобы порции данных были одной длины;
увеличение числа эпох обучения, чтобы влияние маленького батча нивелировалось последующими.

Итоговым решением стало формирование адаптивного batch size: на каждом шаге активного дообучения он вычислялся согласно формуле (1).

$current\_batch\_size =b + \Big \lfloor\frac{n \mod b}{\lfloor\frac{n}{b}\rfloor}\Big\rfloor [1]$

где $b$ — изначальный batch size, а $n$ — текущий размер размеченного набора данных.
Адаптивный подход помог сгладить «просадки» точности и получить монотонно возрастающий график (рис. 6).

Рис. 6. Сравнение использования фиксированного параметра batch size (passive на графике) и адаптивного (passive + flexible на графике)

Примечание: Эти графики показывают работу модели c одним выходом. Но, не умаляя общности, адаптивный batch size можно применять также для модели с тремя выходами. Так мы и сделали в дальнейших экспериментах.

Теперь перейдём непосредственно к исследованию методов активного обучения для нашей задачи.

Uncertainty

Первыми были реализованы наиболее простые стратегии активного обучения из обзорной статьи — методы группы uncertainty sampling. Как следует из названия, стратегия основана на выборе для разметки тех объектов, в предсказании которых модель наименее уверена.

В статье приводятся три варианта подсчёта неуверенности:

1. Минимальная уверенность (англ. Least confident sampling)

В этом виде стратегии эксперту для разметки передаётся объект, наиболее вероятный предсказанный класс для которого характеризуется наименьшей уверенностью:

$x^{*}_{LC} = \underset{x}{\arg\max} \ 1 - P_{\theta }(\hat{y}|x) [2]$

где $\hat{y} = \underset{y}{\arg\max}\ P_{\theta}(y|x)$ — класс с наибольшей вероятностью при классификации моделью, $y$ — один из возможных классов, $x$ — один из объектов набора данных, $x^{*}_{LC}$ — объект, выбранный с помощью стратегии наименьшей уверенности объект.

Подробнее

Эту меру можно понимать так. Допустим, функция потерь на объекте выглядит как $1-\hat{y}$ . В таком случае модель выбирает объект, на котором получит худшую оценку значения функции потерь. Она обучается на нём и тем самым уменьшает значение функции потерь.

Но у этого метода есть недостаток. Например, на одном объекте модель получила следующее распределение по трём классам: {0,5; 0,49; 0,01}, а на другом — {0,49; 0,255; 0,255}. В таком случае алгоритм выберет второй объект, так как его наиболее вероятное предсказание (0,49) меньше, чем у первого объекта (0,5). Хотя интуитивно понятно, что бóльшую информативность для обучения имеет первый объект: вероятности первого и второго класса в предсказании почти равны. Алгоритм стоит модифицировать, чтобы учитывать такие ситуации.

2. Минимальный отступ (англ. Margin sampling)

Согласно этому виду стратегии, алгоритм отправит на экспертизу те объекты, для которых наибольшую вероятность имеют два класса, причём эти вероятности близки:

$x^{*}_{M} = \underset{x}{\arg\min} \ P_{\theta }(\hat{y}_{1}|x) - P_{\theta }(\hat{y}_{2}|x)[3]$

где $\hat{y}_1$ — наиболее вероятный класс для объекта $x$ , $\hat{y}_2$ — второй по вероятности класс.

Подробнее

С точки зрения информации этот метод выигрывает, так как алгоритм учитывает в два раза больше данных о распределении вероятностей классов. Однако и он не идеален, так как не рассматривает распределения по всем остальным классам. При этом, например, в MNIST (популярном наборе данных для классификации рукописных цифр) содержится десять классов — соответственно, во внимание принимается лишь пятая часть информации о распределении. Преодолеть этот недостаток позволяет метод максимальной энтропии.

3. Максимальная энтропия (англ. Entropy sampling)

В этом виде стратегии для измерения неуверенности модели используется мера энтропии:

$x^{*}_{H} = \underset{x}{\arg\max} -\sum \ P_{\theta }(y_{i}|x)\log{P_{\theta }(y_{i}|x)}[4]$

где $y_{i}$ — вероятность $i$ -го класса для объекта $x$ при классификации данной моделью.

Подробнее

Энтропия удобна тем, что она обобщает два метода, которые мы описали выше. Она выбирает объекты обоих типов:

те, где наиболее вероятное предсказание имеет меньшее значение, чем предсказания для других объектов;
и те, для которых два наиболее вероятных класса имеют близкие значения.

Согласно обзорной статье, среди перечисленных методов каждый последующий учитывает больше информации, чем предыдущий. Поэтому изначально ожидалось, что метод entropy sampling окажется наиболее эффективным.

Но практические результаты в рамках решаемой задачи показали расхождение с теорией (рис. 7).

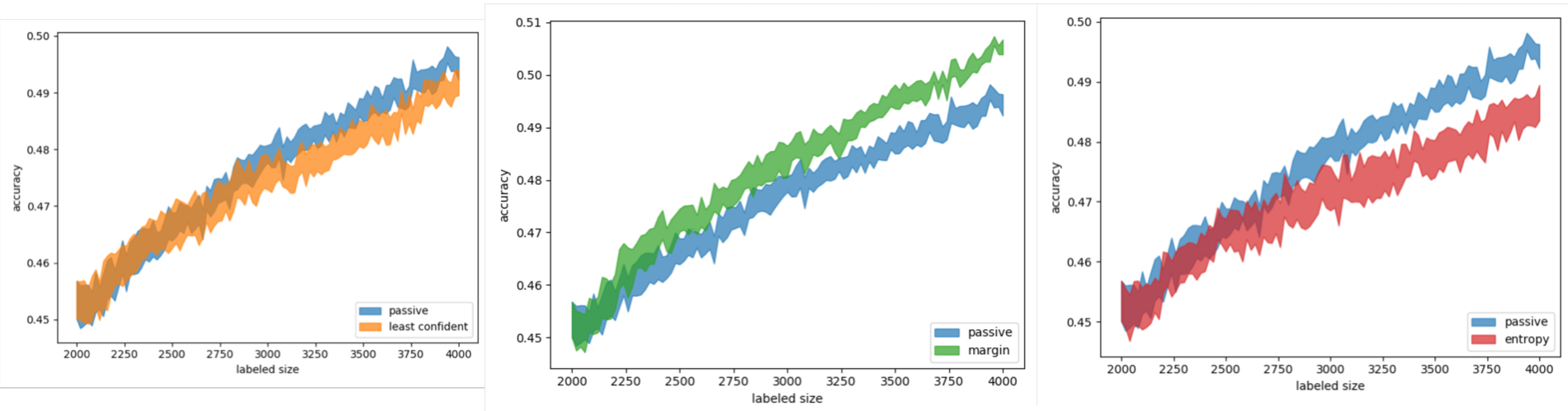
Рис. 7. Результаты сравнения различных видов стратегии uncertainty sampling с пассивным обучением (слева — с методом минимальной уверенности, по центру — с методом минимального отступа, справа — с методом максимальной энтропии)

Как можно заметить, методы least confident и entropy sampling показали себя хуже, чем пассивное обучение со случайным выбором объектов для дообучения. В то же время margin sampling оказался более эффективным.

Чтобы читатели не подозревали, что на реализацию методов могли повлиять баги, сразу отметим: все методы были протестированы также на наборе данных MNIST. И на нём, например, стратегия entropy sampling продемонстрировала результаты, не противоречащие теоретической эффективности метода. Можно сделать вывод, что практическая эффективность описанных методов неоднозначна и зависит от конкретной решаемой задачи.

Перечисленные методы просты с точки зрения реализации и обладают низкой вычислительной сложностью. Можно оценить сложность одного запроса к эксперту как $O(p\log{q})$ , где $p$ — размер неразмеченного набора данных, а $q$ — число объектов в запросе к эксперту. Также эти методы легко применять на практике, так как они не требуют изменения используемой модели.

BALD

Следующая стратегия, о которой пойдёт речь, — BALD sampling (Bayesian Active Learning by Disagreement). Это байесовский подход к измерению неуверенности комитета моделей.

Согласно классификации методов активного обучения, это представитель стратегии query-by-committee (QBC). Её основная идея — в использовании предсказаний нескольких моделей с конкурирующими гипотезами. Можно брать их усреднённое предсказание за основу для uncertainty sampling. Или выбирать для разметки те объекты, в предсказаниях которых модели несогласны в большей степени. Эксперименты проводились с методом QBC на основе Monte Carlo Dropout, речь о котором пойдёт дальше.

Проблема классических байесовских методов для глубокого обучения в том, что необходимо выводить большое количество параметров, —, а это делает обучение моделей в два раза дороже. Поэтому авторы предложили использовать dropout в качестве способа байесовской аппроксимации. Этот подход отличается от привычного применения dropout тем, что он используется во время инференса (на стадии предсказания). Причём для каждого объекта выборки предсказание делается несколько раз одной и той же моделью, но с разными dropout-масками (рис. 8). Такой способ сэмплирования называется Monte Carlo Dropout (MC Dropout) и не требует увеличения затрат памяти при обучении модели. Так с помощью одной модели можно получить несколько предсказаний, которые могут различаться для одного и того же объекта. Несогласие моделей (где они отличаются друг от друга лишь масками dropout) считается на основе Mutual Information (MI). MI здесь представляет собой эпистемическую неопределённость, или неуверенность комитета, — то есть такой вид неопределённости, которая уменьшается с добавлением новых данных. Это согласуется с концепцией активного обучения в целом.

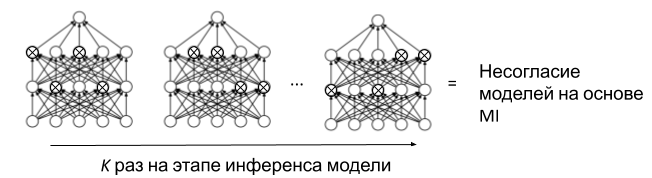
Рис. 8. Иллюстрация MC Dropout для метода BALD

Итак, для начала мы использовали усреднённое предсказание полученного QBC на основе MC Dropout комитета и применили к нему различные методы uncertainty sampling. Это не дало прироста по сравнению с соответствующими методами, использующими только одно предсказание (рис. 9).

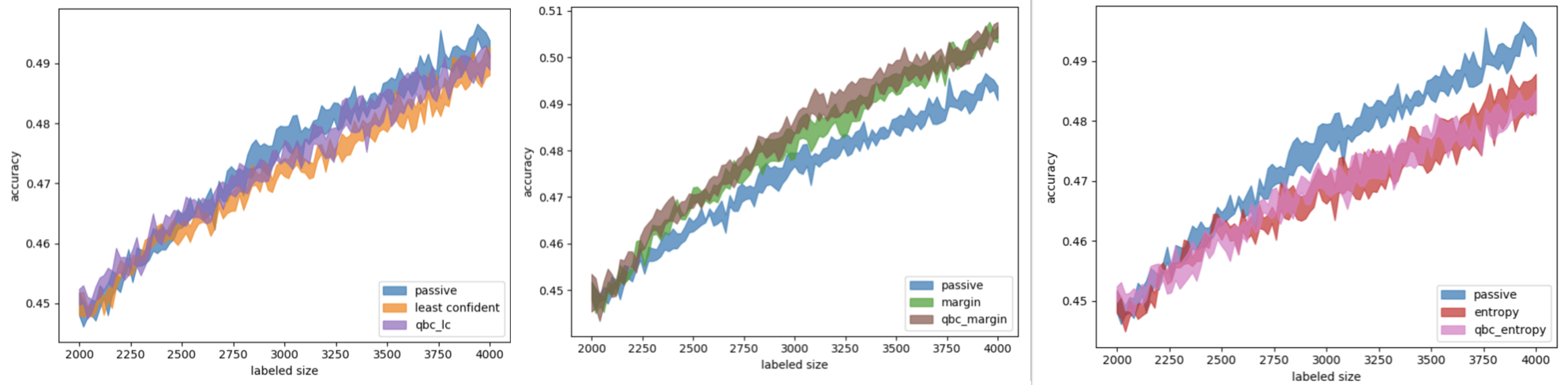
Рис. 9. Результаты сравнения различных видов стратегии uncertainty sampling (на основе QBC и без него) с пассивным обучением (слева — с методом минимальной уверенности, по центру — с методом минимального отступа, справа — с методом максимальной энтропии)

На следующем шаге мы использовали меры несогласия комитета по методу BALD. Как уже было сказано, для этого применяется Mutual Information моделей комитета:

$a_{BALD}=\mathbb{H}(y_1,...,y_n)-\mathbb{E}[\mathbb{H}(y_1,...,y_n|\omega)] [5]$

$\mathbb{E}[\mathbb{H}(y_1,...,y_n|w)]=\frac{1}{k}\sum_{i=1}^{n}\sum_{j=1}^{k}\mathbb{H}(y_i|w_j) [6]$

где $n$ — число классов, $k$ — число моделей в комитете.

Первое слагаемое в формуле (5) представляет собой энтропию усреднённого предсказания комитета, второе — среднюю энтропию каждой модели в отдельности. Таким образом, выбираются только те объекты, в предсказании для которых комитет менее всего согласен. Результаты применения метода BALD представлены на рис. 10.

Рис. 10. Результаты применения стратегии BALD в сравнении с пассивным способом обучения

К сожалению, пока что данный метод не дал ожидаемого результата на долгом запуске эксперимента, несмотря на прирост по сравнению с пассивным методом в начале.
Сложность алгоритмов стратегии query-by-committee в целом и BALD в частности пропорциональна числу предсказаний, сделанных для каждого объекта. В свою очередь, сложность предсказания для каждого объекта аналогична методам uncertainty sampling. Таким образом, сложность одного запроса — $O(kp\log(q))$ , где $p$ — размер неразмеченного набора данных, $q$ — число объектов в запросе к эксперту, а $k$ — число предсказаний, посчитанных для одного объекта.

На практике применить метод BALD может быть нелегко при использовании фреймворка tf.keras, так как он не обладает достаточной гибкостью для работы со слоями. Поэтому в рамках данного проекта мы выбрали фреймворк PyTorch, который позволил не только с легкостью включать dropout во время инференса, но и отключать batch normalization в течение активной фазы, о чем пойдет речь далее.

Инсайт №2: отключение batch normalization в активной фазе

Подобранная модель классификации в своей структуре использует слои batch normalization. Суть подхода batch normalization — в обучении параметров нормализации данных во время обучения и применении найденных параметров во время инференса, или предсказания. Идея, которую мы использовали, состоит в том, чтобы рассматривать активную фазу обучения как этап инференса, и отключать на ней обучение batch normalization. К тому же интуитивно кажется, что такой подход позволит избежать смещения модели. Насколько нам известно, данный вопрос ещё не исследовался в отношении методов активного обучения. Для экспериментов мы взяли за основу метод BALD. Рассмотрим результаты (рис. 11).

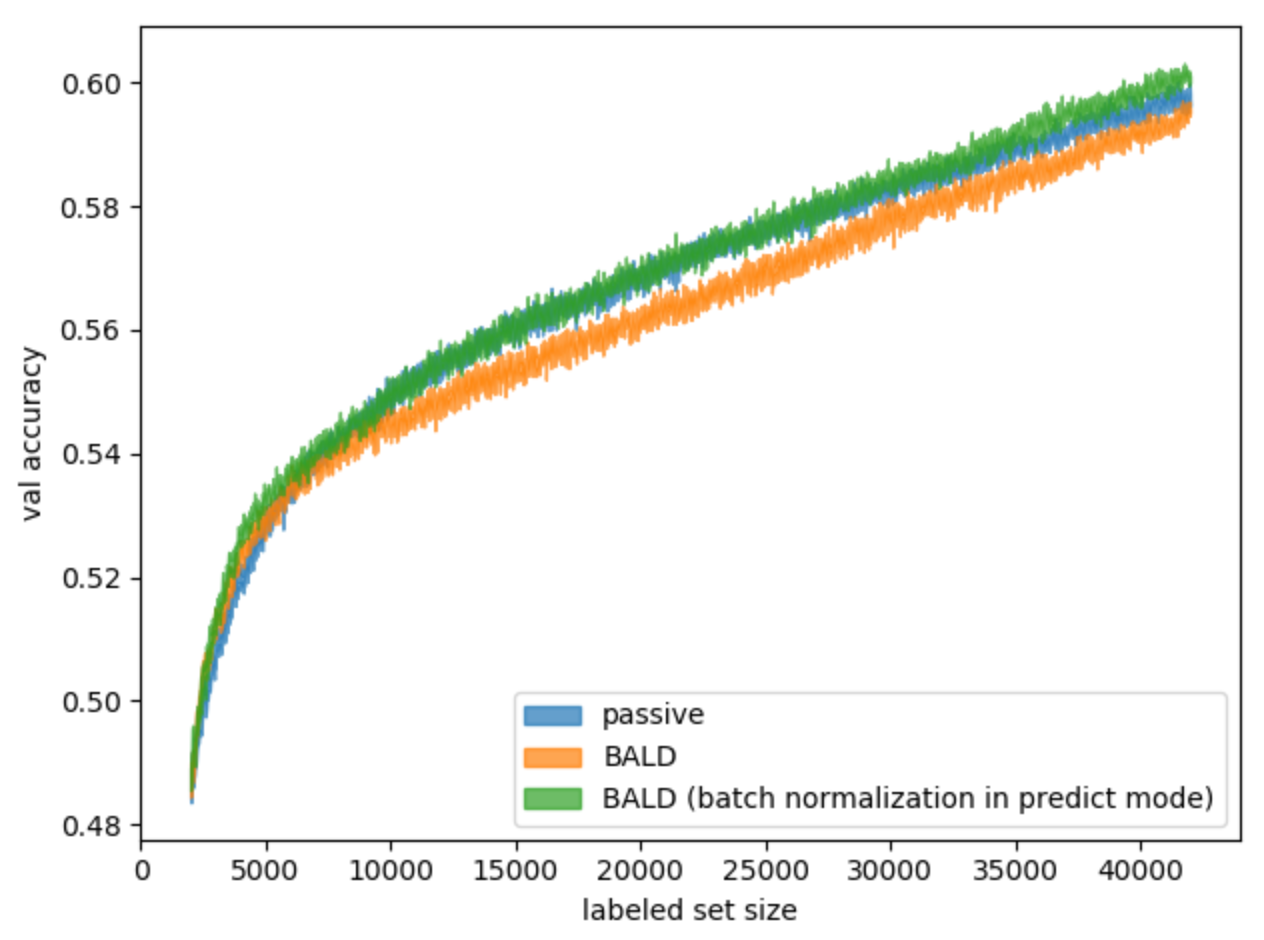
Рис. 11. Результаты отключения batch normalization для метода BALD в сравнении со стандартным методом и пассивным обучением

Как можно судить, такой подход позволил стратегии обойти пассивное обучение, а мы узнали ещё одну неизученную особенность активного обучения.

Чтобы успешно применять отключаемые модули batch normalization, важно располагать большим и разнообразным набором данных для обучения в пассивной фазе. Дело в том, что точность модели сильно зависит от найденных на изначальной выборке параметров нормализации.

Learning loss

Теперь взглянём на проблему активного обучения с другой стороны. Предположим, что неуверенность модели относительно классов тех или иных объектов пропорциональна значению функции потерь от предсказаний для этих объектов. Но пока мы не знаем реального класса объекта, не можем посчитать значение функции потерь.

Создадим вспомогательную модель, принимающую на вход выходы промежуточных и последних слоёв модели. Задача вспомогательной модели — предсказывать значение функции потерь. Мы будем выбирать для разметки те объекты, для которых это значение максимально. Этот метод называется learning loss, подробнее про него можно почитать здесь. Рассмотрим результаты первичных экспериментов, где метод применялся для базовой модели (рис. 12).

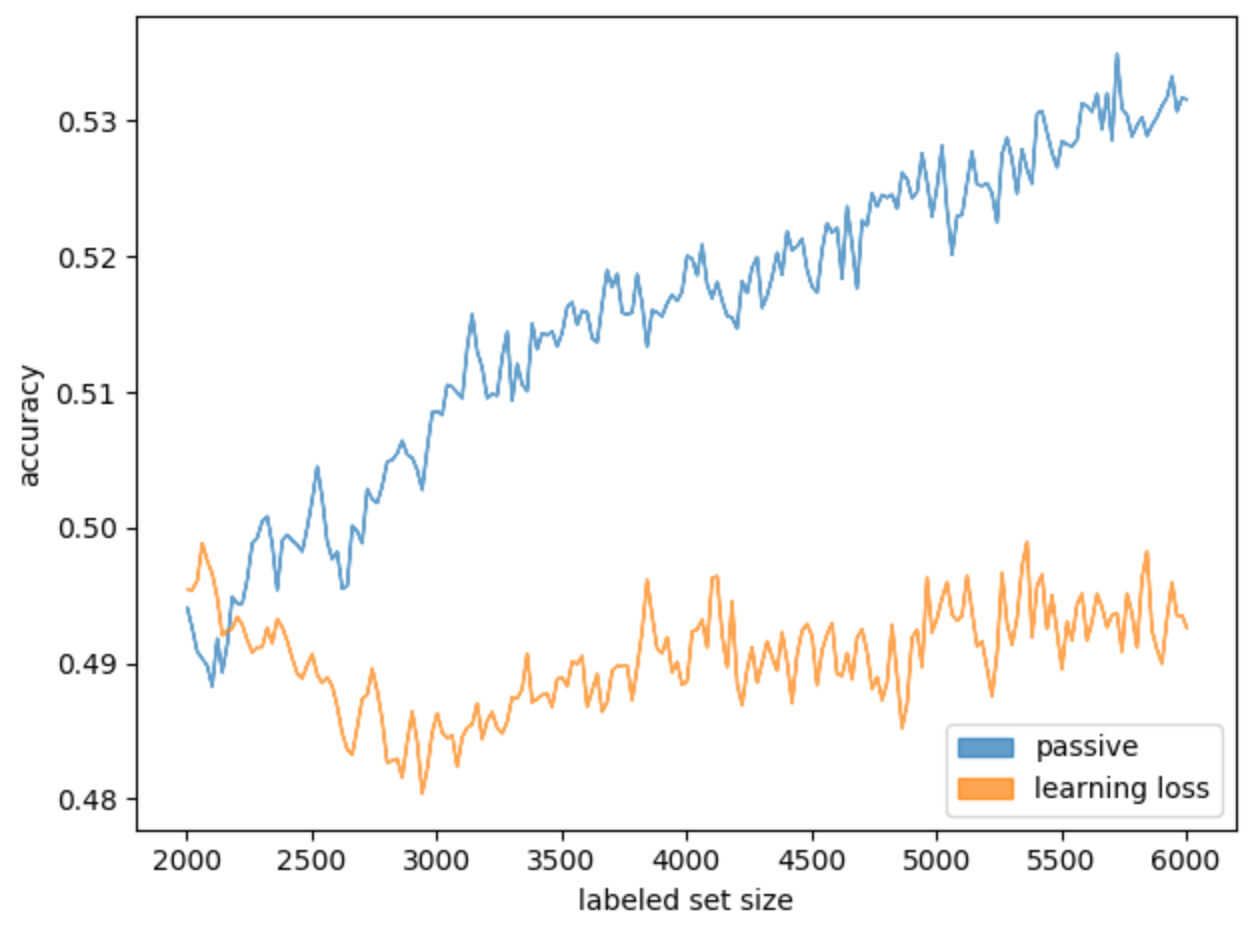
Рис. 12. Результаты применения Learning loss для базовой модели в сравнении с ее пассивным обучением

Метод learning loss не дал прироста по сравнению с пассивным обучением на случайно выбранных объектах. Логично было бы использовать его для моделей других архитектур или отказаться от него как от неэффективного для нашей задачи.
Но мы вместо этого попробуем провести следующий эксперимент. В обычном сценарии активного обучения модель не знает настоящих меток классов, а в нашей задаче они известны. Это позволяет посчитать «идеальный» learning loss: зная настоящую метку класса объекта, будем считать на нём значение функции потерь и добавлять в размеченный набор данных те объекты, у которых оно больше. Назовём такой подход ideal learning loss (рис. 13).

Рис. 13. Результаты применения ideal learning loss для базовой модели в сравнении с её пассивным обучением

Несмотря на ожидания, этот подход показал себя хуже базового метода learning loss.
Мы предположили, что значение функции потерь слабо зависит от точности модели или даже обратно пропорционально ей. Чтобы это проверить, можно построить корреляцию точности модели, обученной на какой-то выборке, и среднего значения функции потерь для объектов этой выборки. Получился следующий экспериментальный пайплайн:

Обучаем модель на начальной выборке (2000 объектов), как для активного обучения;
Выбираем из всего набора неразмеченных данных 10000 объектов (чтобы ускорить подсчёт);
Для выбранных объектов неразмеченной выборки считаем значения функции потерь;
Сортируем объекты по полученным значениям;
Разбиваем на группы по 100 объектов;
Для каждой группы параллельно обучаем на ней модель, стартуя с весов, полученных на шаге 1;
Фиксируем получившиеся точности.

Далее считаем корреляцию Спирмена между точностью модели, обученной на определённой выборке, и средним значением функции потерь по каждому из объектов выборки. А также вычисляем, как средняя точность модели коррелирует со средним значением параметра отступа (из метода margin sampling).

Таблица 1. Корреляции точности и метрик активного обучения для набора данных публикаций ВКонтакте

Как видим, для метода margin sampling корреляция слабая и положительная — то есть, зная отступ, можно быть уверенными, что объект полезен для обучения модели. А в случае c функцией потерь корреляция слабая отрицательная.

Возникает вопрос:, а что если попробовать выбирать для разметки объекты с наименьшими значениями функции потерь?
Как ни странно, эксперименты показали, что и такой вариант тоже не работает ожидаемым образом (рис. 14).

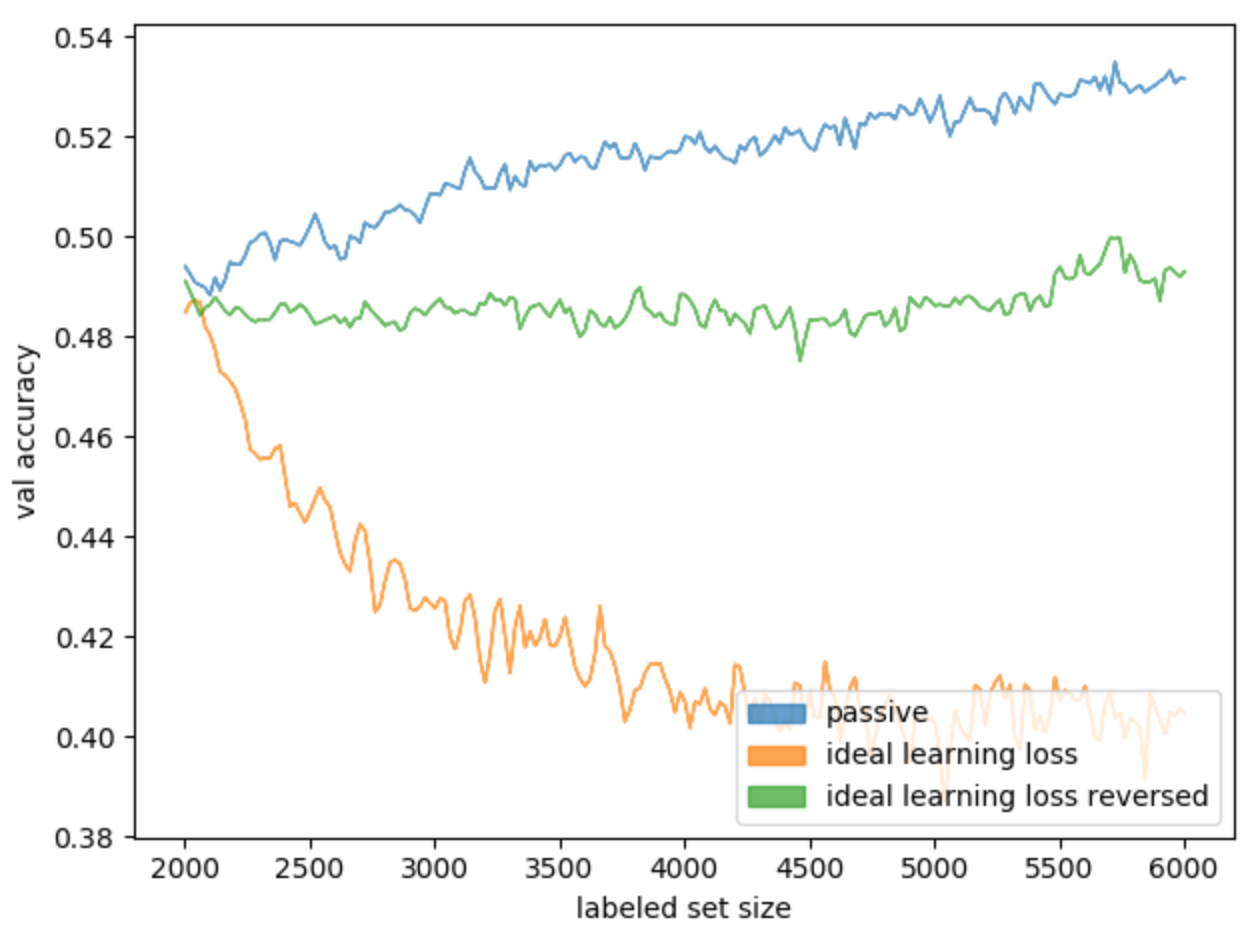
Рис. 14. Результаты применения обратного ideal learning loss для базовой модели в сравнении с прямым ideal learning loss и пассивным обучением

Несмотря на плохие результаты для целевого набора данных, для набора данных MNIST были получены следующие значения корреляции:

Таблица 2. Корреляции точности и метрик активного обучения для набора данных MNIST

При этом сам метод ideal learning loss работает так, как ожидается (рис. 15).

Рис. 15. Активное обучение классификатора символов из набора данных MNIST стратегией ideal learning loss. Синий график — ideal learning loss, оранжевый — пассивное обучение

Получается, что метод, предполагающий, что модели выгоднее обучаться на данных с наибольшим значением функции потерь, работает хорошо. Но при этом он не подходит для нашего набора данных.

Сложность метода learning loss та же, что и для методов uncertainty sampling: $O(p\log{q})$ , где $p$ — размер неразмеченного набора данных, а $q$ — число объектов в запросе к эксперту. Но важно учесть, что при его применении обучать нужно не только основную модель, но и вспомогательную. Этот метод сложнее предыдущих в практическом применении ещё и потому, что требует проводить обучение каскада моделей.

Заключение

Не будем бесконечно раздувать статью, рассказывая обо всех применённых методах и проведённых экспериментах. Здесь мы постарались осветить основные и наиболее интересные. Любопытно, что эффективнее всех оказался самый первый и простой метод margin sampling — результаты его длинного запуска можно увидеть на рис. 16.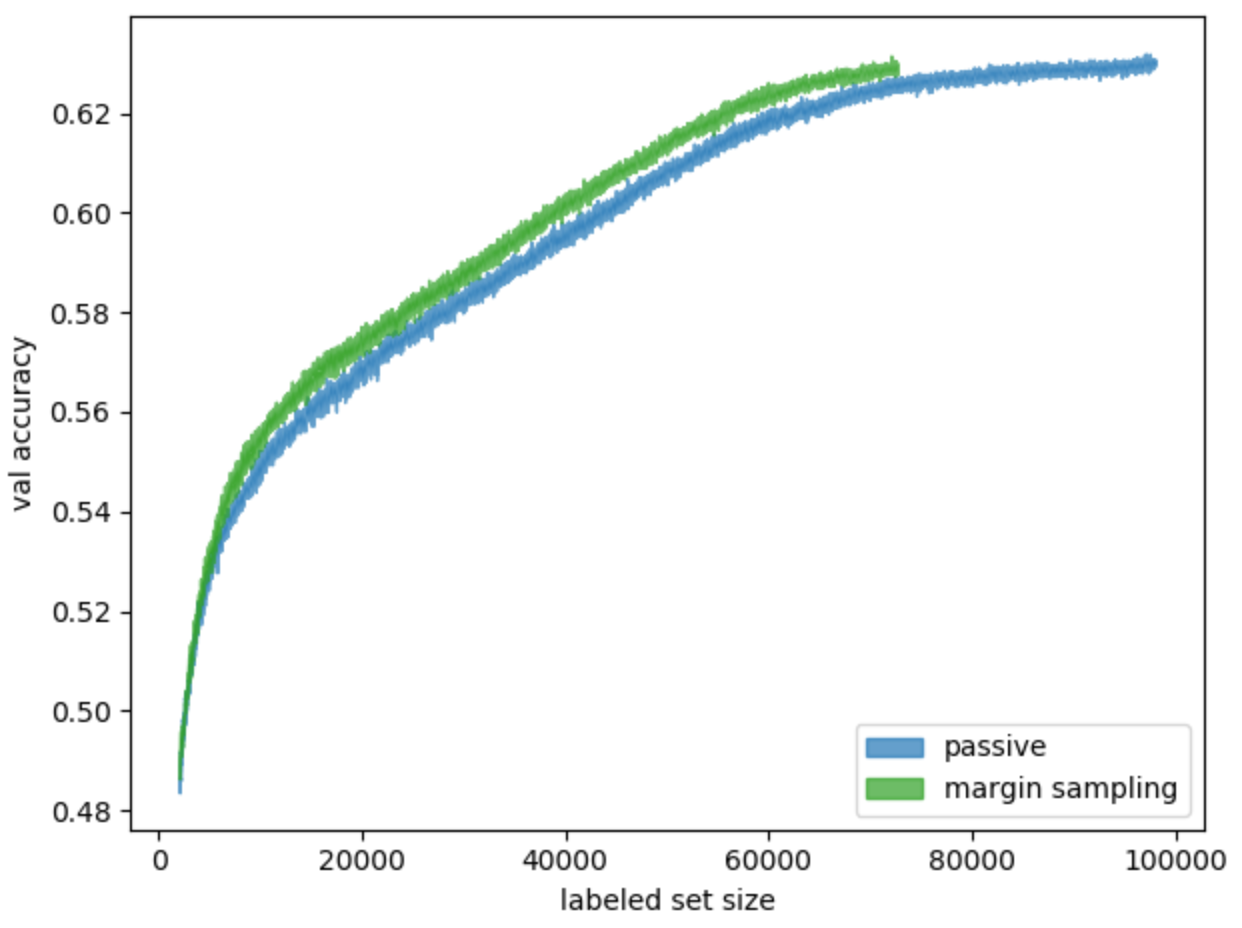

Рис. 16. Сравнение обучения на случайно выбираемых данных (пассивное обучение) и на данных, выбираемых стратегией margin sampling

График показывает: тренируя модель с помощью активного обучения (в нашем случае — стратегией margin sampling), можно достичь предельной точности — такой же, как у модели, обученной пассивным способом. Но при этом использовать на ≈25 тыс. объектов меньше. Экономия ресурсов разметки составит порядка 25% — это довольно значимо.

Также отметим, что в этой задаче эффективность методов была ограничена размером набора данных. В других обстоятельствах выборка может быть значительно больше, а следовательно, у методов активного обучения будет больше вариантов выбора и выше потенциальная эффективность.

Все методы, о которых мы говорили, просты в реализации и обладают невысокой вычислительной сложностью. Но есть моменты, на которые стоит обращать внимание:

выбор batch size;
целесообразность использования для активного обучения подходов, зарекомендовавших себя в глубоких нейронных сетях, — например, batch normalization.