Продиагностируем регрессионные PlayBoy модели?
На пост натолкнул регрессионный анализ PlayBoy моделей бегло на MatLab здесь и продолжение использования этого датасета для анализа выбросов методом опорных векторов на питоне
здесь.
Собственно цель поста — провести беглую диагностику модели регрессионного анализа используя в языке R пакет CAR созданный Джонном Фоксом и сотоварищами, а так же попробуем найти те же выбросы методами регрессии (насколько возможно применять формулировку «выброс» к таким объектам исследований).
Выложил готовый датасет с предыдущих постов (уже переведенный в нашу метрическую систему) предварительно трансформировав его в csv.
Выложил на яндекс диск, предварительно сжав ссылку (для скачивания в R требуется прямая ссылка на файл, а не короткая превью ссылка яндекса) через гуглсервис: https://goo.gl/12XFCG
Y-год журнала
M-Месяц журнала
W — вес реальный, кг (Зависимая переменная, предикаты-ниже)
S — бюст, см
T — талия, см
B — бедра, см
L — рост, см
Диагностировать будем множественную регрессию без трансформации предикатов (т.е. без полиномов, логарифмирования и т.д.) т.к. цель текущего поста-именно диагностика, а не трансформация предикатов.
Итак, скачиваем в датафрейм напрямую по ссылке:
library(car)
df<-read.csv(file=url("https://goo.gl/12XFCG"),header = T,sep=";",as.is = T)
Присваиваем заголовки строк комбинируя сокращенный год и сокращенный месяц:
row.names(df)<-paste(substr(df$Y,start = 3,stop = 4),abbreviate(df$M))
Создаем простую модель
m<-lm(W~S+T+B+L,data=df)
И для начала покажем базовые средства диагностики безотносительно пакета CAR (что это все значит — затронем в конце статьи)
layout(matrix(1:4,nrow = 2));plot(m)
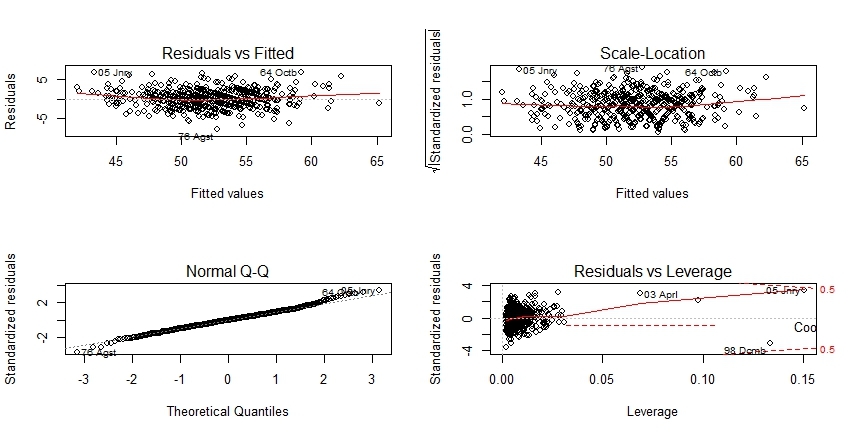
Теперь используем инструментарий CAR
Шаг 1. Тест на нормальность распределения остатков между мат.ожиданиями и факт.значениями зависимой переменной
qqp(m,id.method="identify")
Метод identify позволяет интерактивно получить подписи объектов по кликам мыши на интересных местах графика
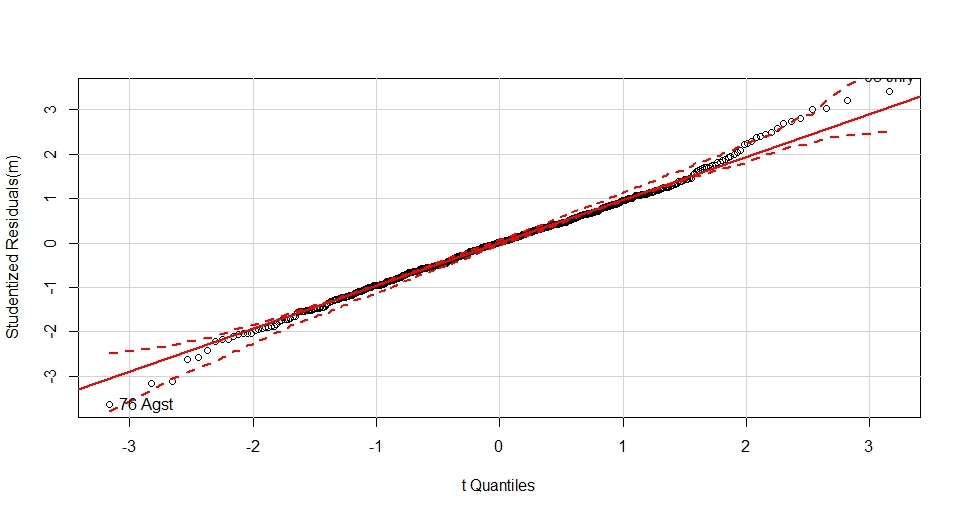
Видно что правый хвост распределения растет выше теоретически нормального, наиболее сильно выбиваются август 76-го и январь 2005 го.
Как видно, распределение не очень хорошо подчиняется нормальному, это же утверждение можно получить через базовый функционал тестом Шапиро-Уилкса, видно что вероятность истинности нормального распределения p-value составляет много меньше нуля
shapiro.test(df$W)
Shapiro-Wilk normality test
data: df$W
W = 0.98205, p-value = 9.131e-07
Один из вариантов приведения распределения зависимой переменной ближе к нормальному- возведение в степень, а вот в какую — ответит функция пакета CAR
> summary(powerTransform(df$W))
bcPower Transformation to Normality
Est.Power Std.Err. Wald Lower Bound Wald Upper Bound
df$W -0.1452 0.4203 -0.969 0.6785
Likelihood ratio tests about transformation parameters
LRT df pval
LR test, lambda = (0) 0.1195765 1 0.729494257
LR test, lambda = (1) 7.5145585 1 0.006120229
Как видно-чуть ближе к нормальному распределению позволит притянуть степень зависимой переменной -0,145
Шаг 2. Тест на отсутствие автокорреляции в остатках
> durbinWatsonTest(m)
lag Autocorrelation D-W Statistic p-value
1 0.1058936 1.786508 0.006
Alternative hypothesis: rho != 0
Значение p-value в данном случае интерпретируется как вероятность отсутствия автокорреляции, низкое значение в 6 тысячных говорит о том что автокорреляция в остатках наблюдается. Тут стоит заметить что функция durbinWatsonTest как и сам тест больше заточены под временные ряды, поэтому в данном случае интерпретировать наличие автокорреляции с лагом =1 довольно сложно.
Шаг 3. Тест на наличие линейной связи между остаками модели (+вклад компоненты в модель) и предикторами
crPlots(m)

Полученный набор графиков позволяет понять-какие компоненты ведут себя нелинейно и требуют преобразований (например логарифмирования). В данном случае стоит обратить внимание на чуть менее выраженную линейность воздействия бедер на мат.ожидание в сравнении с другими предикатами.
В случае выявления нелинейной зависимости в результате обзора графиков,
независимый предикат можно возвести в степень преобразующий данную зависимость в линейную.
расчет степени (и потребности в преобразовании) дает преобразование Бокса-Тидвелла пакета CAR
> boxTidwell(W~S+T+B+L,data=df)
Score Statistic p-value MLE of lambda
S 2.320776 0.0202990 9.995223
T -1.706191 0.0879724 -2.291302
B 6.302344 0.0000000 9.033179
L 2.543296 0.0109812 4.546597
Видно что предикаты бедра и бюст можно попробовать возвести в степень 9 и 10 для более линейного воздействия
Шаг 4 Тест на гомоскедастичность
(постоянство дисперсии остатков)
> ncvTest(m)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.2563336 Df = 1 p = 0.6126503
Нулевая гипотеза в данном случае говорит о вероятности истинности утверждения гомоскедастичности, при этом полученное значение 61% много выше условной 5%-ной границы.
Так же в пакете есть возможность отобразить графически данный тест
spreadLevelPlot(m)
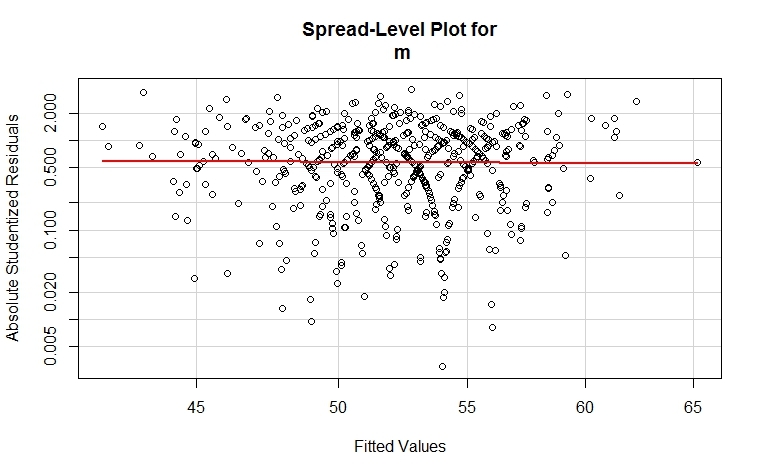
В случае если p-value функции ncvTest
то стоит обратить внимание на то что функция spreadLevelPlot помимо визуализации
выдает в консоль предложение о возведении зависимой переменной в степень для приведения модели к
к состоянию гомоскедастичности
Шаг 5. Тест на мультиколлинеарность предикатов
Наличие взаимной корреляции между влияющими переменными оказывает негативное воздействие на модель, ищем такие ситуации с помощью функции vif
> sqrt(vif(m))>2
S T B L
FALSE FALSE FALSE FALSE
Так же можно отразить визуально наличие корреляции сторонними пакетами
library(corrplot)
cr<-cor(df[,3:6])
corrplot.mixed(corr = cr,upper = "circle",tl.pos = "lt",cl.cex=.5,tl.cex=1.1)
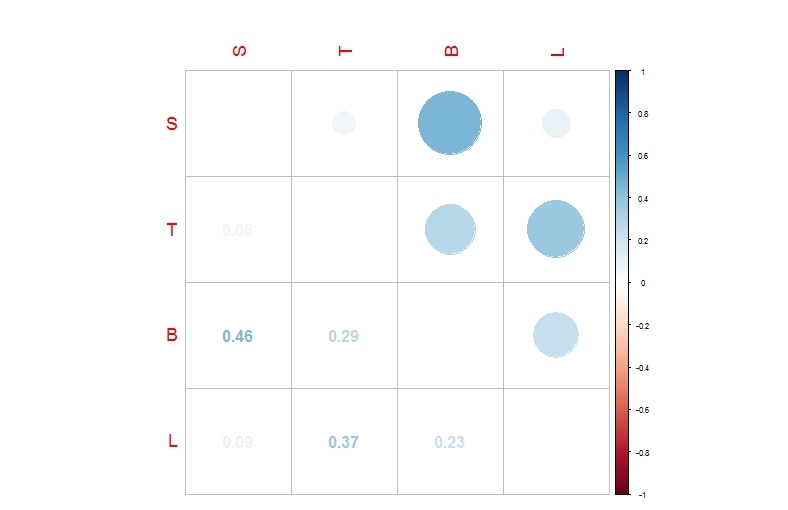
Как видно-наиболее характерная положительная корреляция видна между бедрами и бюстом, но даже в этом случае коэфициент корреляции далек от единицы, так что можно считать что вышеприведенный тест функцией vif подтверждается
Шаг 6. Поиск выбросов по зависимой переменной (по весу)
(отбор происходит по одной в абсолюте, вывод следующей-после удаления из модели предыдущей)
outlierTest(m)
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
76 Agst -3.6393 0.00029703 0.17941
Проверяем вес для августа 1976 года
> subset(df,Y==1976 & M=="August")
M Y S T B L W
76 Agst August 1976 89 61 89 168 45
Кстати, насколько я помню при анализе нормальности распределения эта точка тоже была подписана
Шаг 7.Поиск необычного сочетания предикатов (точки напряженности)
Это тот самый поиск объектов по необычным сочетаниям характеристик на питоне в прошлой статье, только надо понимать что разные алгоритмы дадут разные результаты+насколько я помню там применялся training set, а у нас анализ по полному набору данных.
plot(hatvalues(m),main="Точки напряженности",xlab="Объект",ylab="Значение напряженности")
abline(b = length(m),h = 3*mean(hatvalues(m)),col="red")
identify(x = hatvalues(m),n = length(m),labels = row.names(df))

Шаг 8. Влиятельные объекты на модель по расстоянию Кука (не обязательно точки напряженности)
avPlots(m,ask=F,onepage=T,id.method="identify")
Функция показывает наиболее влиятельный объект на зависимую переменную-вес (не обязательно в высоких значениях зависимой переменной, но и в области низких значений)
Плюсом данных графиков является тот важный момент что становится понятно-в ккую сторону качнется мат.ожидание зависимой переменной если удалить определенный объект.
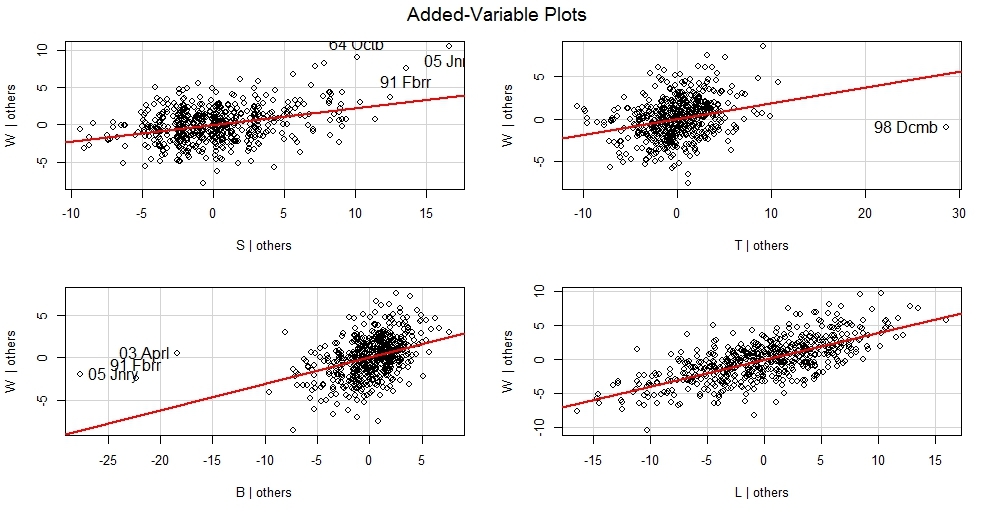
Влиятельным объектом в модели на вес с точки зрения бюста может быть январь 2005 го.
Можем детализировать сначала посчитав статистику всех бюстов и весов
> summary(df[,c(3,7)])
S W
Min. : 81.00 Min. :42.00
1st Qu.: 86.00 1st Qu.:49.00
Median : 89.00 Median :52.00
Mean : 89.29 Mean :52.17
3rd Qu.: 91.00 3rd Qu.:54.00
Max. :104.00 Max. :68.00
и затем детализировав интересующий объект
> subset(df,Y==2005 & M=="January")
M Y S T B L W
05 Jnry January 2005 91 61 61 165 50
Видно что бюст бодро держится в 3-м квартиле при весе объекта значительно ниже медианы
Бонус пакета (общая диаграмма)
influencePlot(m,id.method = "identify")
абсцисса-напряженность, ордината-выброс, размер окружности-влиятельность на модель
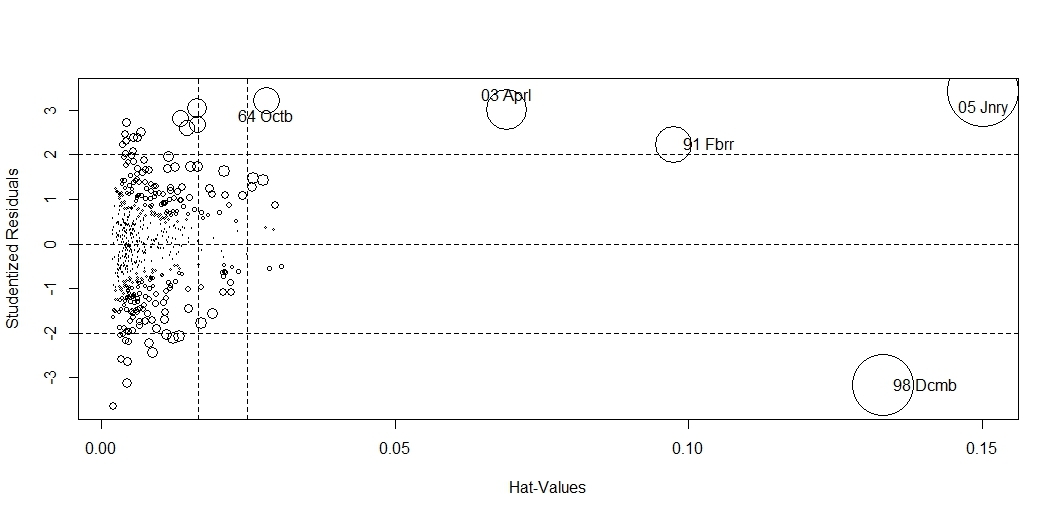
P.S.
Теперь как и обещал-интепретация базовой графикиd в начале статьи в контексте вышеописанных инструментов.
левый верхний — тест на линейность зависимости
правый верхний график-тест на гомоскедастичность
левый нижний- тест на нормальность распределения
правый нижний график- абсцисса это уровень напряженности (необычного сочетания предикатов), ордината-стандартизованные остатки позволяющие судить о выбросе, расстояние Кука- зона влиятельных на модель объектов.
Таким образом есть возможность выбора-анализировать модель урезанным базовым функционалом либо расширенным из пакета CAR (я описал бегло и по-диагонали лишь часть того что в нем есть)
