Применение R при вычислениях с повышенной точностью
Периодически встречаются задачи, даже в обыденной жизни, когда разрядной точности float64/int64 оказывается недостаточной для того, чтобы получить ответ с требуемой точностью. Метаться в поисках другого инструмента? Тоже вариант.
А можно этого и не делать, а проявить любопытство и узнать, что для вычисления с произвольной точностью давным давно сделана библиотека GNU MPFR к которой есть обертки почти к всем языкам. Практика показывает, что с этой библиотекой вообще мало кто знаком, что вызвано, наверное, особенностями программ обучения в ВУЗ-ах и последующим программистским мейнстримом.
Библиотека хороша и заслуживает того, чтобы на нее обращали внимание, хотя бы в рамках расширения кругозора. По R к ней есть обертка Rmpfr. Ниже приведу простенький пример на задачках для школьников (ну не трогать же проектные данные под NDA) и затрону ряд классических граблей, на которые наступают почти сразу же.
Является продолжением предыдущих публикаций.
Берем для примера задачу №39 из конкурса 2019/2020 учебного года в Квантике:
Положительные числа x и y таковы, что в неравенстве ниже левая дробь больше правой. Что больше: x или y?
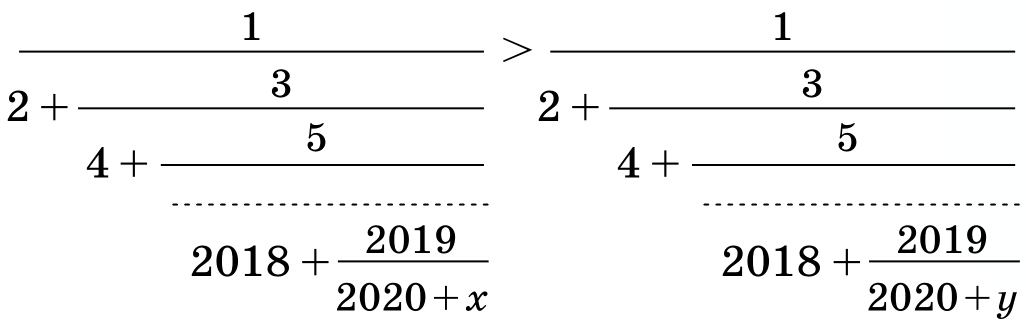
Естественно, что решать ее надо аналитически (знакопеременное неравенство), но это не повод не использовать ее в качестве демонстрации.
Рисуем простенький код для вычисления последовательности значений дробей. Можно сразу финальное значение задать, но тут же демосцена для mpfr, так что движемся мелкими шажками.
library(tidyverse)
library(magrittr)
options(digits=15)
frec <- function(stopval, n, x){
res <- ifelse(n == stopval,
(stopval - 1) + stopval/(stopval + 1 + x),
(n - 1 ) + n / (frec(stopval, n + 2, x))
)
res
}
frec_wrap <- function(stopval, x){
res <- frec(stopval = stopval, n = 1, x = x)
print(glue::glue("{stopval}: {res}"))
res
}
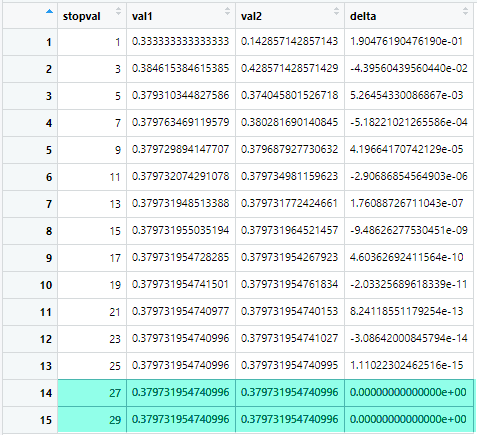
sol_df <- tibble(stopval = seq(1, 29, by = 2)) %>%
mutate(val1 = purrr::map_dbl(stopval, frec_wrap, x = 1),
val2 = purrr::map_dbl(stopval, frec_wrap, x = 5),
delta = val1 - val2)И вот ведь незадача, уже на 14-ой итерации (стоп число = 29) нам недостаточно точности чтобы различить значения дробей. А надо считать аж до 2019!
Все пропало? Ну нет, возьмем в руки Rmfpr. Первая идея — давайте просто заменим float64 на mpfr и дело в шляпе.
library(tidyverse)
library(magrittr)
library(Rmpfr)
frec2 <- function(stopval, n, x){
if(n == stopval){
(stopval - 1) + stopval/(stopval + 1 + x)} else {
(n - 1 ) + n / (frec2(stopval, n + 2, x))
}
}
frec2_wrap <- function(stopval, x){
.precision <- 5000
res <- frec2(stopval = mpfr(stopval, .precision),
n = mpfr(1, .precision),
x = mpfr(x, .precision)
)
print(glue::glue("{stopval}: {formatMpfr(res, drop0trailing = TRUE)}"))
res
}
sol2_df <- tibble(stopval = seq(1, 29, by = 2)) %>%
mutate(val1 = purrr::map(stopval, frec2_wrap, x = 1),
val2 = purrr::map(stopval, frec2_wrap, x = 5))Но не тут то было. Худо бедно посчитать можно, но в tibble уже засунуть затруднительно. Распечатать или провести математические действия путем векторизации невозможно.
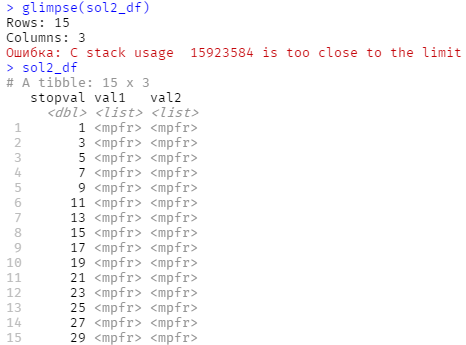
Проблема №1: tibble в последней инкарнации не принимает типы данных, отличные от vctrs. Все прочие (а mpfr является S4 классом) только через list-column. Как-то неудобненько и не наглядненько.
Кстати, переход на vctrs не только здесь дает знать. Он начинает рвать на простых операция присвоения в несуществующие колонки, пример кода:
for(jj in 1:12){
# поскольку прямое присвоение, то мы ничего перед этим не чистим
flags_df[[glue("bp_2_{jj}_T")]] <- flags_df[[glue("bp_2_{jj}_in")]] & flags_df[[glue("flag_2_{jj}")]]
flags_df[[glue("bp_2_{jj}_F")]] <- flags_df[[glue("bp_2_{jj}_in")]] & ! flags_df[[glue("flag_2_{jj}")]]
}Проблема №2:
list-column автоматически отменяет векторизацию и требует ручной итерации. При этом разницу между двумя mpfr числами придется опять помещать в list-column.
Проблема №3
Посмотреть визуально rpfm числа не представляется возможным. StackOverflow предлагает массу вариантов с регулярными выражениями по выцеплению визуального представления. Плюс это еще засунуть в итератор. И эти люди говорят нам об элегантности подходов в R?
Проблемы? Да-да-да! Это все потому что R, а не Python! Мы всегда знали!
Нет. Просто RTFM, вспоминаем хорошо забытое старое и решаем все одним взмахом.
- Проблема №1. Решается все просто — свет клином на
tibbleне сошелся. Можно использовать старый проверенныйdata.frame. - Проблема №2. В
rpfmесть абстрация для вектора чисел с повышенной точностью над которыми можно проводить мат. операции обычным образом, не привлекая итераторы. Аdata.frameвполне себе стерпит такой вектор. - Проблема №3. Читаем документацию и используем векторизированную функцию
formatMpfrдля создания текстовых представлений чисел.
Легкость бытия возвращается в первозданном виде.
library(tidyverse)
library(magrittr)
library(Rmpfr)
# решаем через повышенную точность
frec2 <- function(stopval, n, x){
if(n == stopval){
(stopval - 1) + stopval/(stopval + 1 + x)} else {
(n - 1 ) + n / (frec2(stopval, n + 2, x))
}
}
frec2_wrap <- function(stopval, x){
# browser()
.precision <- 5000
res <- frec2(stopval = mpfr(stopval, .precision),
n = mpfr(1, .precision),
x = mpfr(x, .precision)
)
print(glue::glue("{stopval}: {formatMpfr(res, drop0trailing = TRUE)}"))
res
}
sol_df <- data.frame(stopval = seq(111, 119, by = 2)) %>%
# сразу преобразуем список mpfr чисел в вектор
mutate(val1 = new("mpfr", unlist(purrr::map(stopval, frec2_wrap, x = 1))),
val2 = new("mpfr", unlist(purrr::map(stopval, frec2_wrap, x = 5))),
delta = val1 - val2)
sol_txt_df <- sol_df %$%
tibble(stopval = stopval,
val1_txt = formatMpfr(val1, drop0trailing = TRUE),
val2_txt = formatMpfr(val2, drop0trailing = TRUE),
delta_txt = formatMpfr(delta, drop0trailing = TRUE))P.S. Желающие поспорить в поисках истины могут не утруждаться. Это больше похоже на задачку в стиле головоломок, чем на серьезную претензию. А те, кто умеет читать между строк, обязательно ознакомятся с GNU MPFR.
Предыдущая публикация — «Применение R в задаче обновления кассового ПО?».
