Positive-Unlabeled learning and where to find it
Привет! В этой статье я начну рассказ про Positive-Unlabeled (PU) learning. Расскажу, что это за область машинного обучения и в каких задачах она применяется. В конце будет немного про наше применение PU learning для поиска коррупции в аукционах государственных закупок.

Кто я
Меня зовут Дмитрий Иванов. Я учусь на 2-м курсе аспирантуры по экономике в Питерской Вышке. Работаю в исследовательской группе «Агентные Системы и Обучение с Подкреплением» в JetBrains Research, а также в международной лаборатории Теории Игр и Принятия Решений в ВШЭ. Помимо PU learning я интересуюсь обучением с подкреплением и исследованиями на стыке машинного обучения и экономики.
Преамбула
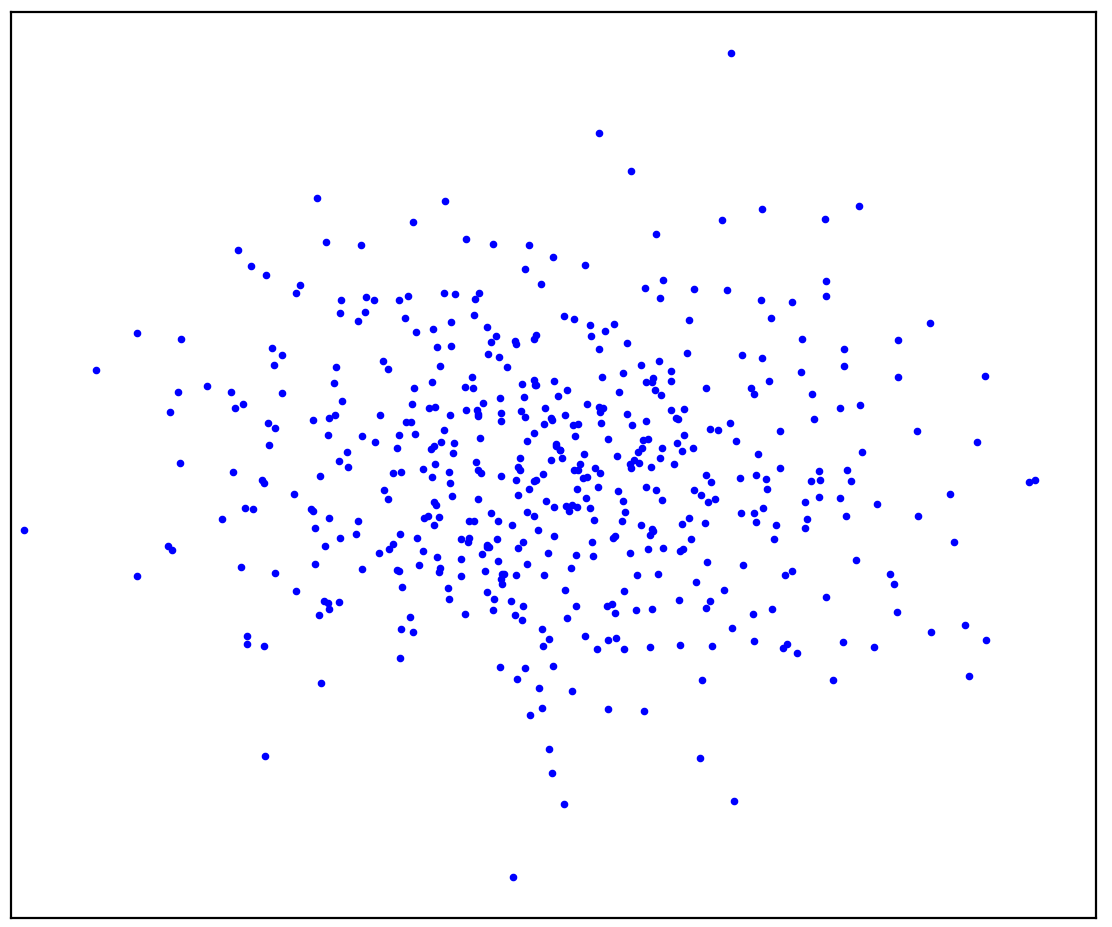
Рис. 1а. Положительные данные
На рисунке 1а изображен набор точек, сгенерированных некоторым распределением, которое мы назовем положительным. Все другие возможные точки, которые не принадлежат положительному распределению, назовем отрицательными. Попробуйте мысленно нарисовать линию, отделяющую представленные положительные точки от всех возможных отрицательных. Кстати, такую задачу называют «детекция аномалий».

Рис. 1 б. Эллипс отделяет положительные данные от возможных отрицательных
Возможно, вы представили себе что-то подобное рисунку 1 б: обвели данные в эллипс. На самом деле, так и работают многие методы детекции аномалий.
Теперь немного изменим задачу: пусть у нас есть дополнительная информация, что отделять положительные точки от отрицательных должна прямая линия. Попробуйте мысленно нарисовать ее.
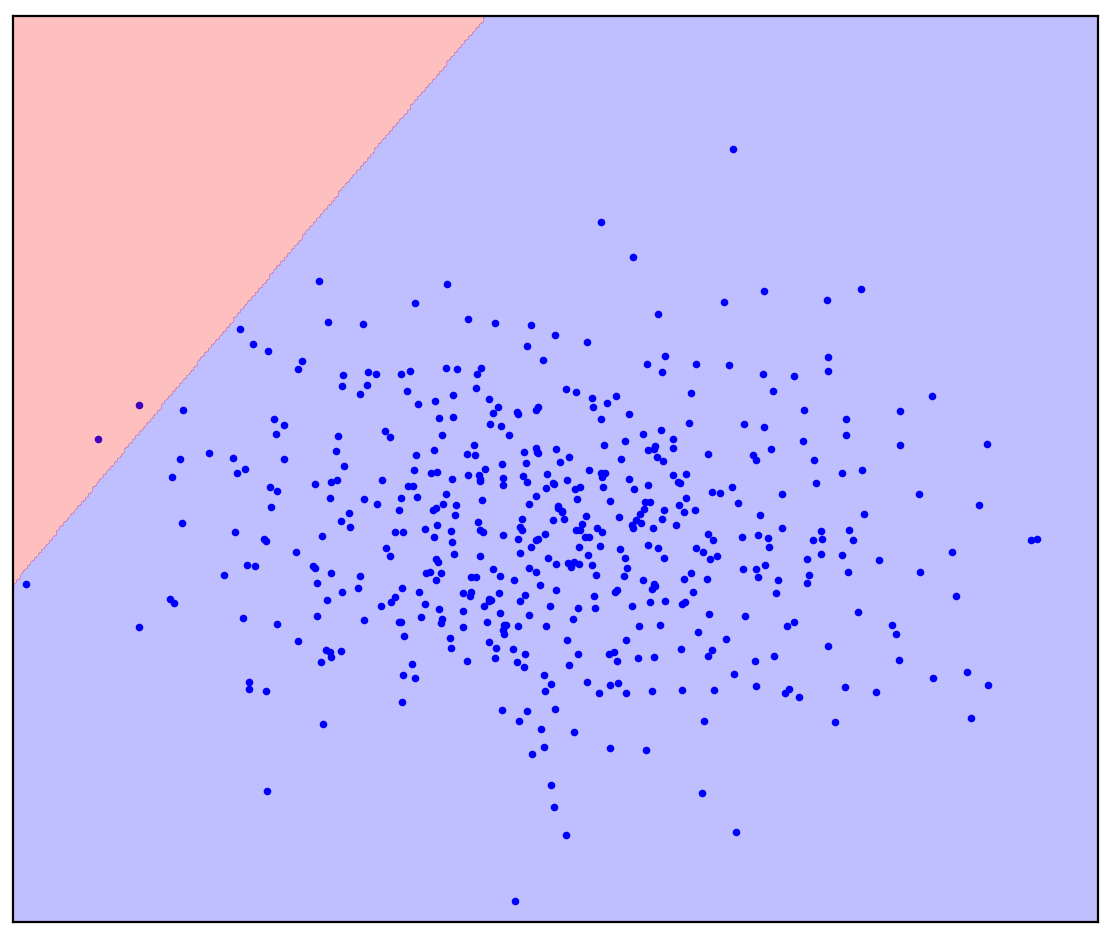
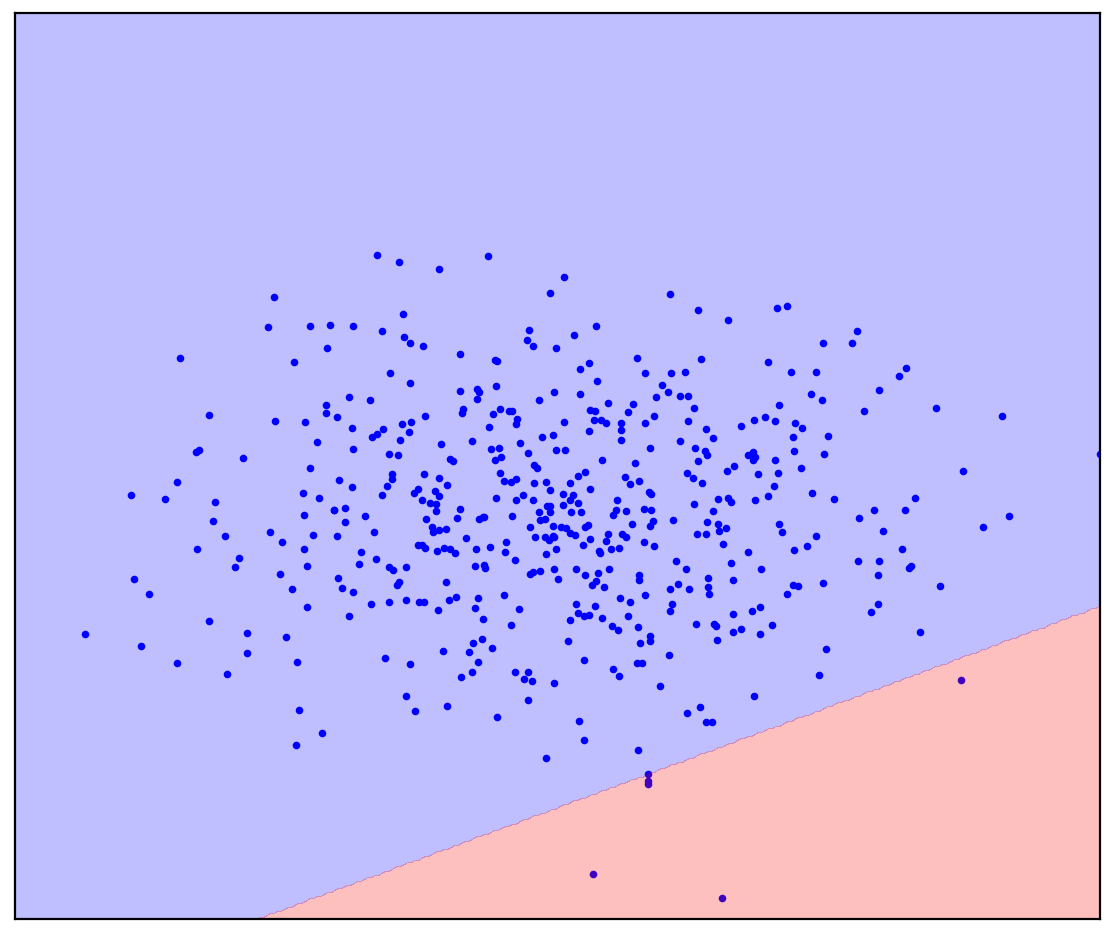
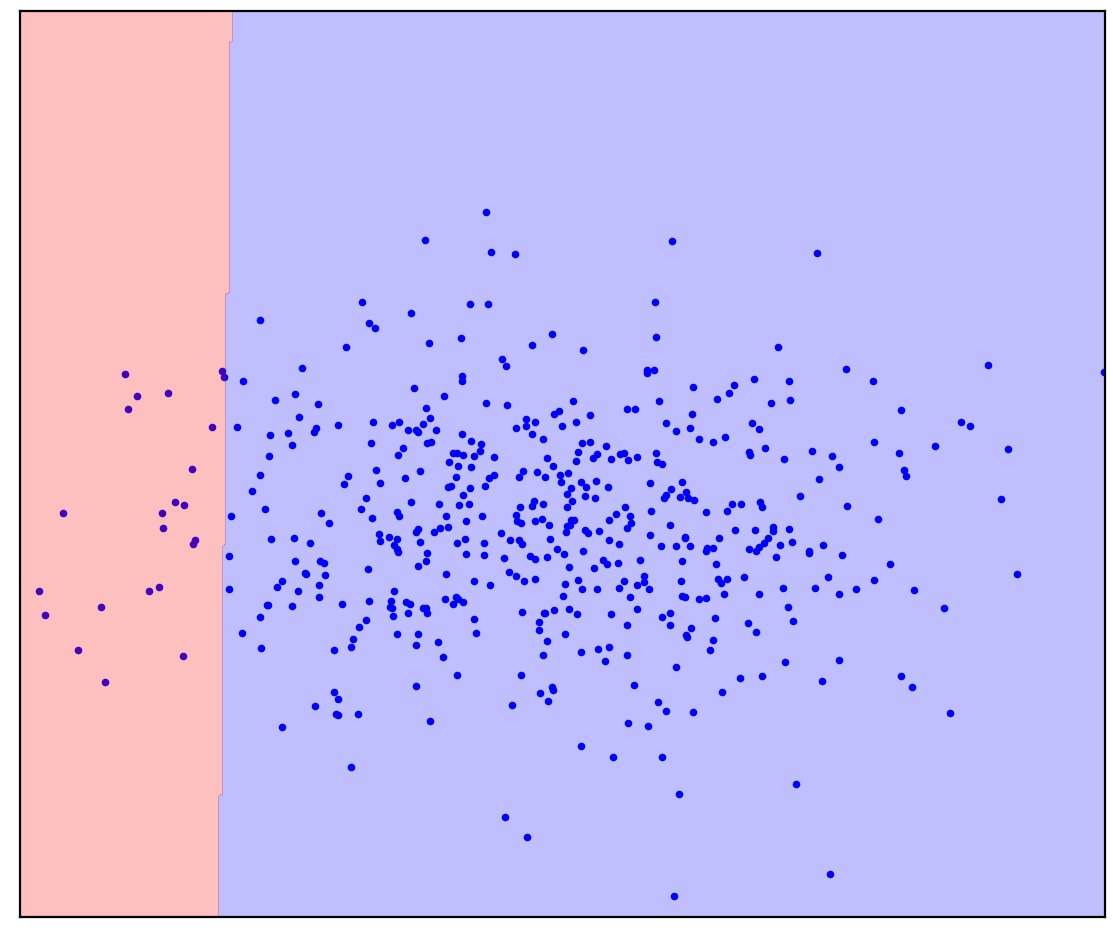
Рис. 1в. Прямые отделяют положительные данные от возможных отрицательных (прямые предсказаны алгоритмом детекции аномалий One-Class SVM)
В случае прямой разделяющей линии нет однозначного ответа. В каком направлении рисовать прямую ― непонятно.
Теперь я добавлю на рисунок 1 г неразмеченные точки, которые содержат смесь положительных и отрицательных. В последний раз я попрошу вас приложить ментальное усилие и представить прямую, разделяющую положительные и отрицательные точки. Но на этот раз можно использовать неразмеченные данные!

Рис. 1 г. Положительные (синие) и неразмеченные (красные) точки. Неразмеченные точки состоят из положительных и отрицательных

Рис. 1д. Прямая отделяет положительные точки от отрицательных исходя из неразмеченных данных
Стало легче! Хотя мы заранее не знаем, как сгенерирована каждая конкретная неразмеченная точка, мы можем примерно их разметить, сравнив с положительными. Красные точки, похожие на синие, вероятно, положительные. Наоборот, непохожие — наверняка отрицательные. В итоге, несмотря на то что у нас нет «чистых» отрицательных данных, информацию о них можно получить из неразмеченной смеси и использовать ее для более точной классификации. Это и делают алгоритмы Positive-Unlabeled learning, о которых я хочу поведать.
Введение
Positive-Unlabeled (PU) learning можно перевести как «обучение на основе положительных и неразмеченных данных». По сути, PU learning — это аналог бинарной классификация для случаев, когда имеются размеченные данные только одного из классов, но доступна неразмеченная смесь данных обоих классов. В общем случае мы даже не знаем, сколько данных в смеси соответствует положительному классу, а сколько — отрицательному. На основе таких наборов данных мы хотим построить бинарный классификатор: такой же, как и при наличии чистых данных обоих классов.
В качестве игрушечного примера рассмотрим классификатор картинок кошек и собак. У нас есть немного картинок кошек и еще много картинок как кошек, так и собак. На выходе мы хотим получить классификатор: функцию, предсказывающую для каждой картинки вероятность того, что изображена кошка. Заодно классификатор может разметить нашу имеющуюся смесь картинок на кошек и собак. При этом вручную размечать картинки для обучения классификатора может быть сложно / дорого / долго / невозможно, хочется без этого.
PU learning — задача довольно естественная. Данные, которые встречаются в реальном мире, часто являются грязными. Возможность обучаться на грязных данных относительно качественно кажется полезным лайфхаком. Несмотря на это, я встречал парадоксально мало людей, которые слышали о PU learning, и еще меньше тех, кто знал бы о каких-то конкретных методах. Поэтому я решил рассказать об этой области.

Рис. 2. Jürgen Schmidhuber and Yann LeCun, NeurIPS 2020
Применение PU learning
Я неформально разделю случаи, в которых PU learning может быть полезен, на три категории.
Первая категория, наверное, наиболее очевидная: PU learning можно применять вместо обычной бинарной классификации. В некоторых задачах данные по своей природе немного грязные. В принципе, это загрязнение можно игнорировать и использовать обычный классификатор. Но можно совсем немного изменить лосс-функцию при тренировке классификатора (Kiryo et al., 2017) или даже сами предсказания уже после тренировки (Elkan & Noto, 2008), и классификация станет точнее.
В качестве примера рассмотрим идентификацию новых генов, отвечающих за развитие каких-либо заболеваний (disease genes). Стандартный подход — считать уже найденные disease genes положительными данными, а все остальные гены — отрицательными. Очевидно, что в этих отрицательных данных могут присутствовать еще не найденные disease genes. Более того, сама задача состоит в поиске таких disease genes среди «отрицательных» данных. Это внутреннее противоречие замечают здесь: (Yang et al., 2012). Исследователи отошли от стандартного подхода и рассмотрели гены, не относящиеся к уже обнаруженным disease genes, как неразмеченную смесь, а затем применили методы PU learning.
Другой пример — обучение с подкреплением на основе демонстраций эксперта. Задача заключается в том, чтобы обучить агента действовать так же, как эксперт. Этого можно добиться при помощи метода generative adversarial imitation learning (GAIL). В GAIL используется GAN-подобная (generative adversarial networks) архитектура: агент генерирует траектории так, чтобы дискриминатор (классификатор) не мог отличить их от демонстраций эксперта. Недавно исследователи из DeepMind заметили, что в GAIL дискриминатор решает задачу PU learning (Xu & Denil, 2019). Обычно экспертные данные дискриминатор считает положительными, а сгенерированные — отрицательными. Это приближение достаточно точно в начале обучения, когда генератор не способен производить данные, похожие на положительные. Однако по мере обучения сгенерированные данные все больше походят на экспертные, пока не станут неотличимыми для дискриминатора в конце обучения. По этой причине исследователи (Xu & Denil, 2019) считают сгенерированные данные неразмеченными данными с непостоянной пропорцией смеси. Позднее похожим образом был модифицирован GAN при генерации картинок (Guo et al., 2020).

Рис. 3. PU learning как аналог стандартной PN классификации
Во второй категории PU learning может быть применен для детекции аномалий как аналог одноклассовой классификации (OCC). Мы уже видели в Преамбуле, чем конкретно неразмеченные данные могут помочь. Все методы ОСС без исключений вынуждены делать предположение о распределении отрицательных данных. Например, разумно обвести положительные данные в эллипс (гиперсферу в многомерном случае), вне которого все точки отрицательны. В этом случае мы предполагаем, что негативные данные распределены равномерно (Blanchard et al., 2010). Вместо того чтобы делать такие предположения, методы PU learning могут оценить распределение отрицательных данных на основе неразмеченных. Это особенно важно, если распределения двух классов сильно пересекаются (Scott & Blanchard, 2009). Один из примеров детекции аномалий с применением PU learning — обнаружение фейковых обзоров (Ren et al., 2014).

Рис. 4. Пример фейкового обзора
Детекция коррупции в аукционах российских государственных закупок
В третью категорию применения PU learning можно отнести задачи, в которых ни бинарная, ни одноклассовая классификации не могут быть использованы. В качестве примера я расскажу про наш проект по детекции коррупции в аукционах российских государственных закупок (Ivanov & Nesterov, 2019).
По законодательству полные данные по всем аукционам госзакупок размещаются в открытом доступе для всех желающих потратить месяц на их парсинг. Мы собрали данные по более чем миллиону аукционов, проведенных с 2014 по 2018 года. Кто, когда и сколько поставил, кто выиграл, в какой период проходил аукцион, кто проводил, что закупал ― все это в данных есть. Но, разумеется, нет метки «тут коррупция», так что обычный классификатор не построишь. Вместо этого мы применили PU learning. Основное предположение: участники с нечестным преимуществом всегда выигрывают. Используя это предположение, проигравших в аукционах можно рассмотреть как честных (положительных), а победителей ― как потенциально нечестных (неразмеченных). При такой постановке методы PU learning могут находить подозрительные паттерны в данных на основе тонких различий между победителями и проигравшими. Конечно, на практике возникают сложности: необходимы аккуратный дизайн признаков для классификатора, анализ интерпретируемости его предсказаний, статистическая проверка предположений о данных.
По нашей очень консервативной оценке около 9% аукционов в данных коррумпированы, вследствие чего государство теряет около 120 миллионов рублей в год. Потери могут показаться не очень большими, но исследуемые нами аукционы занимают лишь около 1% рынка госзакупок.


Рис. 5. Доля коррумпированных аукционов госзакупок в разных регионах России (Ivanov & Nesterov, 2019)
Завершающие ремарки
Чтобы не создавалось впечатление, что PU — решение всех бед человечества, упомяну подводные камни. В обычной классификации чем больше у нас данных, тем точнее можно построить классификатор. Более того, увеличивая количество данных до бесконечности, мы можем приближаться к идеальному (по формуле Байеса) классификатору. Так вот, основной подвох PU learning в том, что это — ill-posed задача, то есть задача, которая не решается однозначно даже при бесконечном количестве данных. Ситуация становится лучше, если известна пропорция двух классов в неразмеченных данных, однако определение этой пропорции — тоже ill-posed задача (Jain et al., 2016). Лучшее, что мы можем определить — это интервал, в котором находится пропорция. Более того, методы PU learning часто не предлагают способов оценки этой пропорции и считают ее известной. Есть отдельные методы, которые ее оценивают (задача называется Mixture Proportion Estimation), однако часто они медленны и/или нестабильны, особенно когда два класса представлены в смеси сильно неравномерно.
В этом посте я рассказал про интуитивное определение и применения PU learning. Помимо этого, я могу рассказать про формальное определение PU learning с формулами и их пояснениями, а также про классические и современные методы PU learning. Если этот пост вызовет интерес — напишу продолжение.
Список литературы
Blanchard, G., Lee, G., & Scott, C. (2010). Semi-supervised novelty detection. Journal of Machine Learning Research, 11(Nov), 2973–3009.
Elkan, C., & Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining — KDD 08, 213. https://doi.org/10.1145/1401890.1401920
Guo, T., Xu, C., Huang, J., Wang, Y., Shi, B., Xu, C., & Tao, D. (2020). On Positive-Unlabeled Classification in GAN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8385–8393.
Ivanov, D. I., & Nesterov, A. S. (2019). Identifying Bid Leakage In Procurement Auctions: Machine Learning Approach. ArXiv Preprint ArXiv:1903.00261.
Jain, S., White, M., Trosset, M. W., & Radivojac, P. (2016). Nonparametric semi-supervised learning of class proportions. ArXiv Preprint ArXiv:1601.01944.
Kiryo, R., Niu, G., du Plessis, M. C., & Sugiyama, M. (2017). Positive-unlabeled learning with non-negative risk estimator. Advances in Neural Information Processing Systems, 1675–1685.
Ren, Y., Ji, D., & Zhang, H. (2014). Positive Unlabeled Learning for Deceptive Reviews Detection. EMNLP, 488–498.
Scott, C., & Blanchard, G. (2009). Novelty detection: Unlabeled data definitely help. Artificial Intelligence and Statistics, 464–471.
Xu, D., & Denil, M. (2019). Positive-Unlabeled Reward Learning. ArXiv:1911.00459 [Cs, Stat]. http://arxiv.org/abs/1911.00459
Yang, P., Li, X.-L., Mei, J.-P., Kwoh, C.-K., & Ng, S.-K. (2012). Positive-unlabeled learning for disease gene identification. Bioinformatics, 28(20), 2640–2647.
