Поиск кратчайшей траектории на поверхности реконструированного МРТ изображения30.07.2023 21:01

Привет, Хабр! Хочу рассказать о том, как я решал задачу связанную с обработкой и визуализацией томографических изображений, а именно — измерение и поиск кратчайшей траектории на поверхности 3D изображения. Одна из областей применения — измерение антропометрических данных на КТ/МРТ исследованиях.

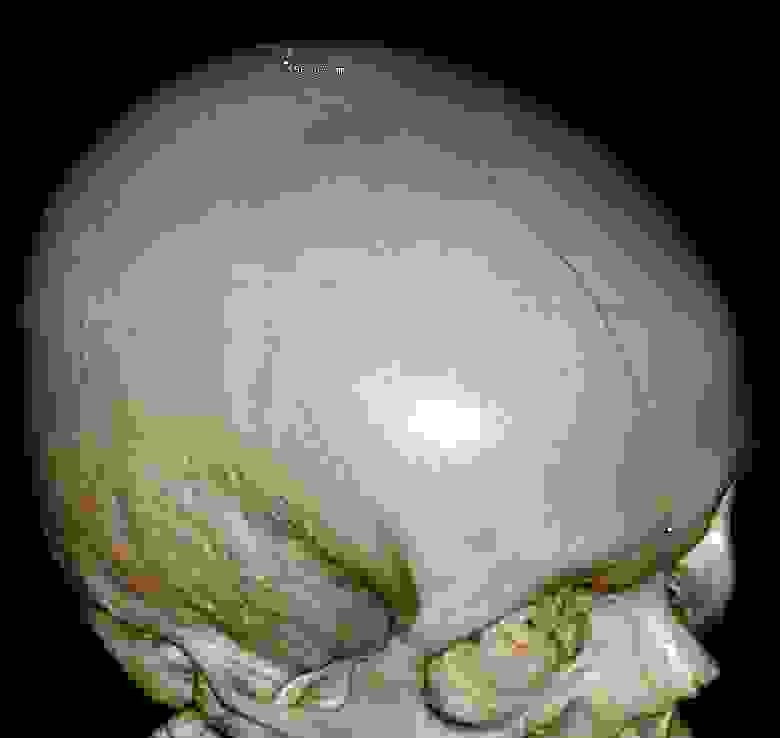
Измерение длины черепа на КТ изображении

Данная статья представляет собой небольшой обзор решения задачи, в процессе реализации, пришлось столкнуться со многими подводными камнями. Поэтому текст будет соответствовать хронологической последовательности, в которой и происходила реализация алгоритма.

Содержание

Воксельный объем
Классические алгоритмы поиска пути
Проблема Евклидова кратчайшего пути
Планирование пути под любым углом
Проблема ориентации воксельной поверхности
Полигонализация
Поиск пути на полигональной сетке
Заключение

Воксельный объем

Воксельный объем представляет собой трехмерный куб — структура моделирующая собой объемный объект, где каждый элемент такой структуры называется вокселем. Воксели не содержат информацию о своих координатах в пространстве, поэтому координаты вычисляются из их позиции в объеме.

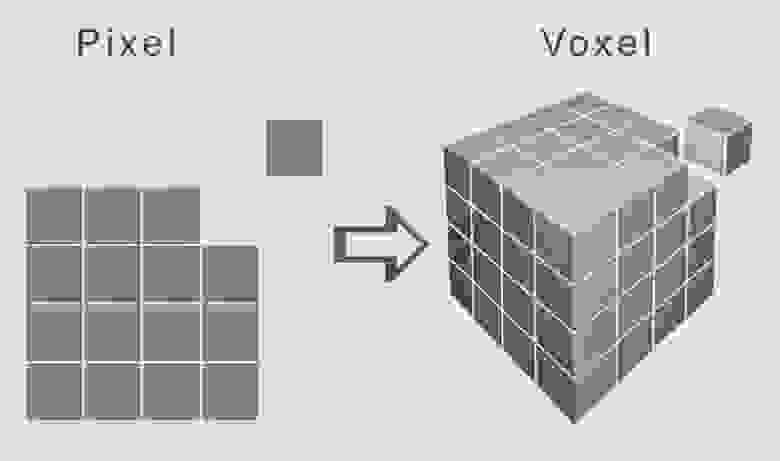
Связь между вокселями и пикселями

Воксели хорошо подходят для описания моделей имеющие внутреннюю структуру, например для моделирования сплошных сред или трехмерной реконструкции томографических исследований. А каждый воксель может характеризоваться определенными значениями, такими как скорость частицы или рентгеновская плотность вещества.

Воксельный рендер

Существует множество статей о практическом применения воксельных моделей в медицине. Интересующийся читатель может ознакомиться с сегментацией томографических данных или же прочесть про методику обнаружения центральной линии сосудов.

Для простоты изложения и понимания материала, в данной статье будут рассматриваться 2D изображения, но используемы алгоритмы с легкостью расширяются и на объемное пространство.

Классические алгоритмы поиска пути

Тем, кто хоть немного знаком с теорией графов, наверняка слышали про обход графа в ширину (BFS) и в глубину (DFS), или же про алгоритм Дейкстры. Эти методы являются базовыми для решения задачи поиска пути. Только вот алгоритм Дейкстры, в отличии от двух других позволяет найти не только наличие траектории, но и выдать кратчайший из возможных. Могу порекомендовать онлайн-книгу, в которой достаточно обширно рассказывается на тему поиска пути.

Большинство алгоритмов поиска имеют одну общую идею, которая заключается в обходе графа, и порядок обхода является ключевым моментом, определяющий название алгоритма. Если же посещение вершин будет организовано в виде очереди, то получится поиск в ширину, а если в качестве структуры данных будет стек — поиск в глубину. Также можно представить обход над очередью с приоритетом, то в таком случае получится алгоритм Дейкстры. Одним из самых известных алгоритмов поиска кратчайших путей является A*, который представляет собой модификацию Дейкстры.

Может показаться, что решение поставленной задачи очевидно, ведь узлы графа — это видимые воксели, связь между двумя соседними векселями образуют ребра, а вес ребра — это расстояние между вокселями, нужно всего лишь реализовать поиск пути методом A*. Но есть один нюанс. Данный алгоритм действительно является эффективным и оптимальным, но он прежде всего ориентирован на дискретные области. И первая проблема — это применение алгоритма к воксельному объему, представленный в виде дискретного набора элементов, которые в свою очередь описывают непрерывное (в данном случае Евклидово) пространство.

Проблема Евклидова кратчайшего пути

Классические алгоритмы распространяются на дискретном наборе траекторий, и в случае двухмерной регулярной сетки количество направлений будет равно 8, с шагом в 45 градусов.

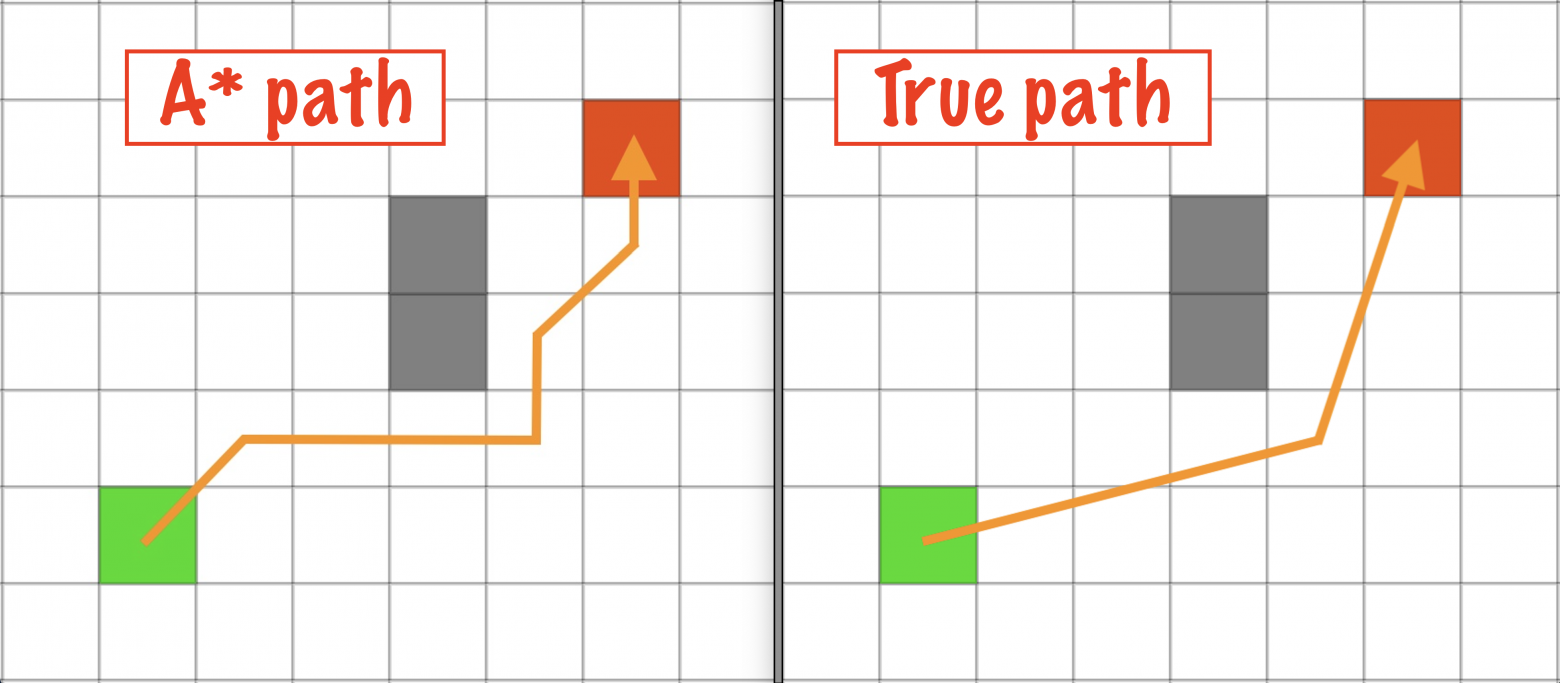
Различие межу алгоритмом A* и реальной траекторией

Планирование пути под любым углом

Алгоритмы планирования пути под любым углом направлены на получение оптимальных или почти оптимальных траекторий с учетом непрерывности пространства, и естественно это приводит к росту стоимости вычислений.

Post-smoothing

Самый простой подход приводящий к улучшению траектории, заключается в применении итеративного сглаживания на этапе пост обработки пути. Казалось бы, что это хорошее решение, которое способно решить нашу проблему, но к сожалению реальность сурова — у такого подхода есть недостаток, который заключается в том, что сглаживание не всегда оптимально, например, если сглаживаемая точка будет проходит через препятствие, то сглаживание на данном участке недопустимо и больше не будет производится.

Рассмотрим пример. Видим, что весь путь можно удачно сгладить в прямую линию, что бы он прошел под препятствием. Но на одной из итерации сглаживания, траектория пройдет по недопустимому маршруту, тем самым, ожидаемого результата данный алгоритм не достигнет.

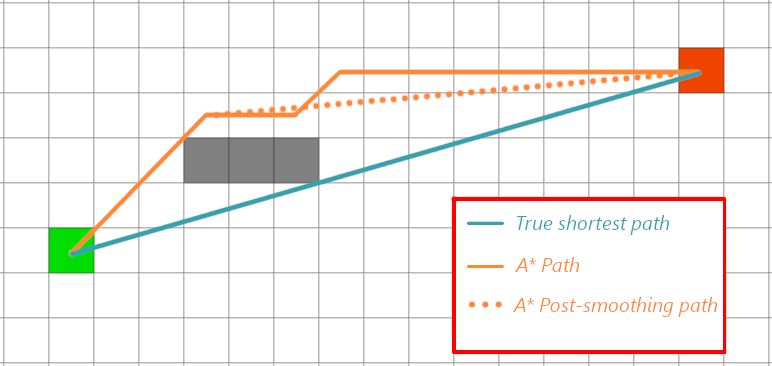
Сглаживание не дает оптимальной траектории

Алгоритм Lazy Theta*

Более эффективным подходом будет применение алгоритмов, основанных на трассировке траектории между точками, с целью определения видимости между узлами. Одним из таких алгоритмов является Theta* [1], который является модификацией A*. В свою очередь у данного метода есть оптимизация в виде Lazy Theta* [2], которая приводит к меньшим вычислительным затратам.

Вкратце алгоритм Theta* заключается в том, что при распространении волны поиска, следующая точка проверяет видимость до родительской точки текущего узла, и в случае успеха родитель текущего узла становится также родителем следующей точки, в противном случае родителем становится текущая вершина. Таким образом, при обнаружении препятствия на пути к цели, алгоритм ищет наилучшую точку в направлении цели на линии между текущей точкой и предыдущей наилучшей точкой, а не пересчитывает путь до каждой точки, это похоже на формирование некого графа видимости.

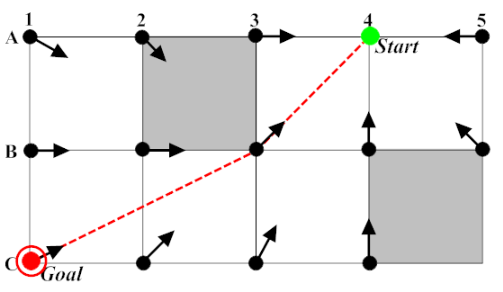
Theta*

Проблема ориентации воксельной поверхности

Может показаться, что все подводные камни решены и вышеуказанного подхода будет достаточно. Но, на самом деле мы только на пол пути.

Вспомним, что путь строится на поверхности, поэтому рассмотрим бинарное изображение и вычислим контур его поверхности. Вычисление контура бинарного изображения можно осуществить через морфологические операции. Контур изображения представляет собой разность между исходным изображением и его эрозией.

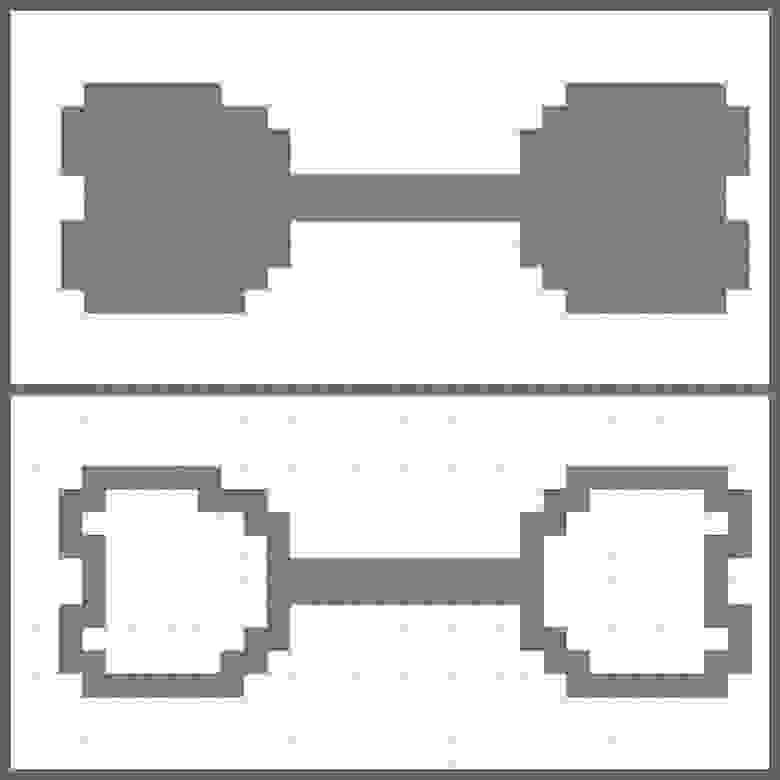
Исходное изображение (сверху) и его контур (снизу)

Если посмотреть, как будет вести себя алгоритм Lazy Theta* на данном примере, то мы обнаружим, что естественное поведение алгоритма не всегда приводит к ожидаемому результату. В момент, когда поверхности располагаются очень близко, то они образуют некий «мост», по которому путь может перейти на другую сторону поверхности. Это видно на изображение ниже, где существует ожидаемый маршрут (зеленый) и реальный (красный)

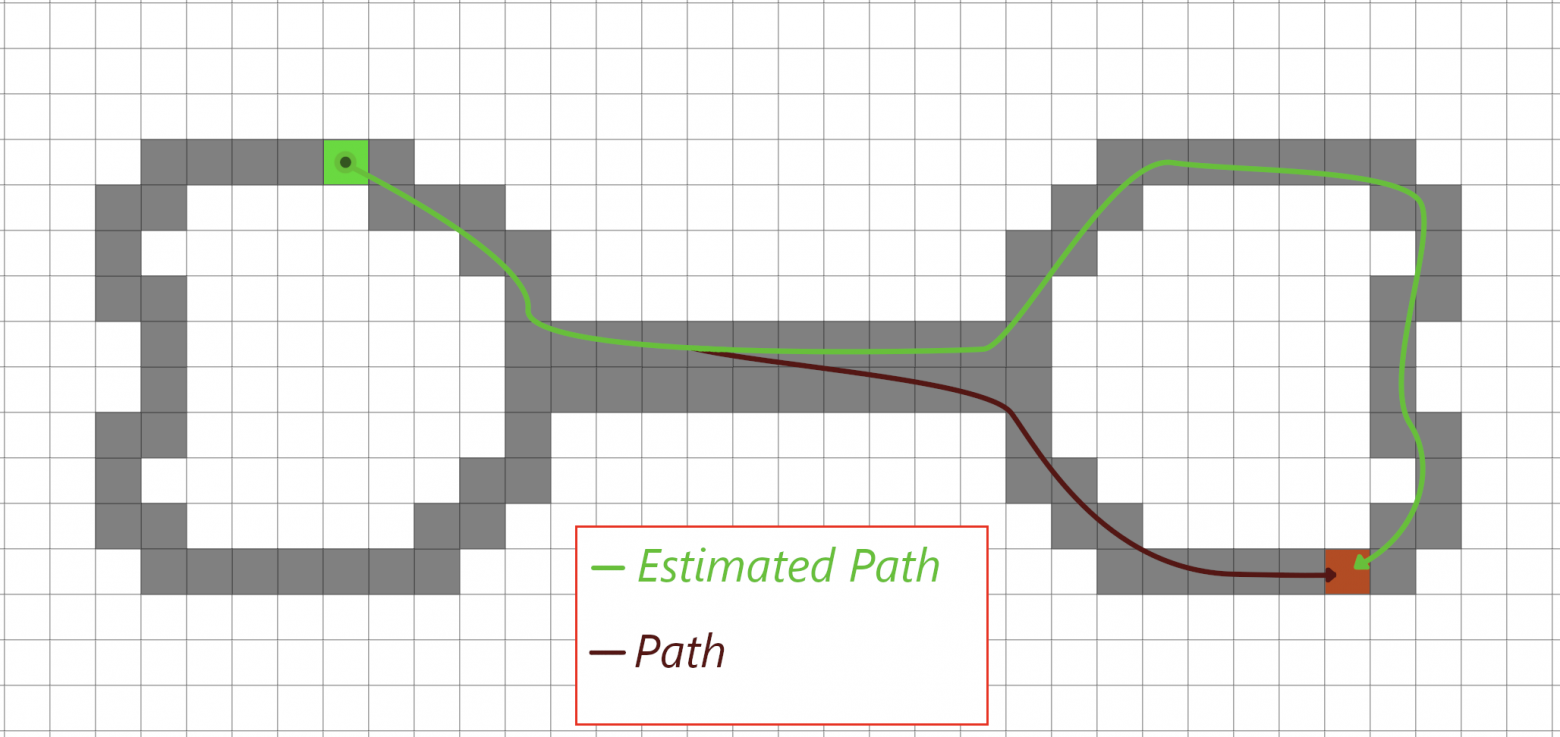
Полигонализация

Проблема пиксельного (воксельного) представления объекта приводит к тому, что необходимо определение полигональной границы объекта на изображении. Для этого используется алгоритмы, которые определяют границы контура и создают полигоны, соединяющие эти границы. Одним из простых алгоритмов полигонализации является алгоритм марширующих кубов.

Алгоритм марширующих кубов является трехмерным алгоритмом, который используется для создания поверхностей в трехмерном пространстве. Однако, алгоритм также может быть адаптирован для работы в двумерном пространстве.

Идея алгоритма марширующих кубов в 2D состоит в том, чтобы разбить изображение на набор прямоугольников (пиксели 2×2). Затем, используя информацию о значениях пикселя в углах каждого прямоугольника, алгоритм создает линии, которые проходят через грани прямоугольника. Таким образом, создается набор линий, которые соединяются, чтобы создать границу объекта.

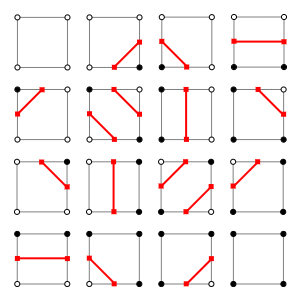
Вариации 2D полигонализации

Алгоритм марширующих кубов в 3D основан на той же идее, что и в 2D. Но вместо того, чтобы использовать прямоугольники, он разделяет объемное изображение на набор кубов, каждый из которых состоит из 8 вокселей (вершин). Затем, используя информацию о значениях вокселя внутри каждого куба, алгоритм создает поверхности, которые проходят через грани куба. Таким образом, создается набор треугольников, которые соединяются, чтобы создать границу объекта.

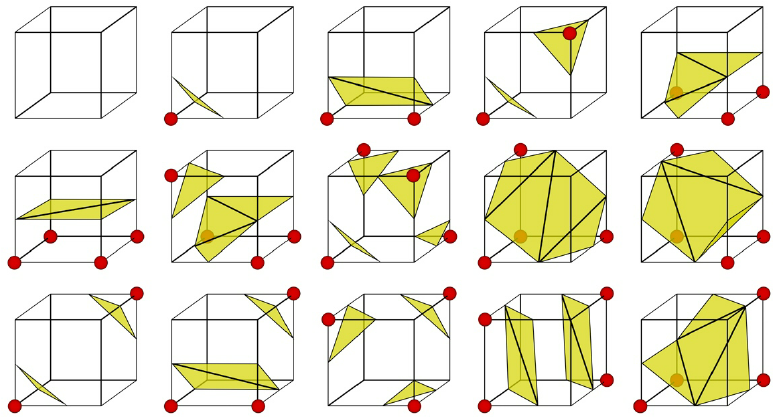
Вариации 3D полигонализации

Посмотрев на результат марш. кубов, можно заметить, что полигонализация изображения предоставляет более точную информацию о поверхности, чем морфологическое оконтуривание, а именно — отсутствие «лишних» связей.

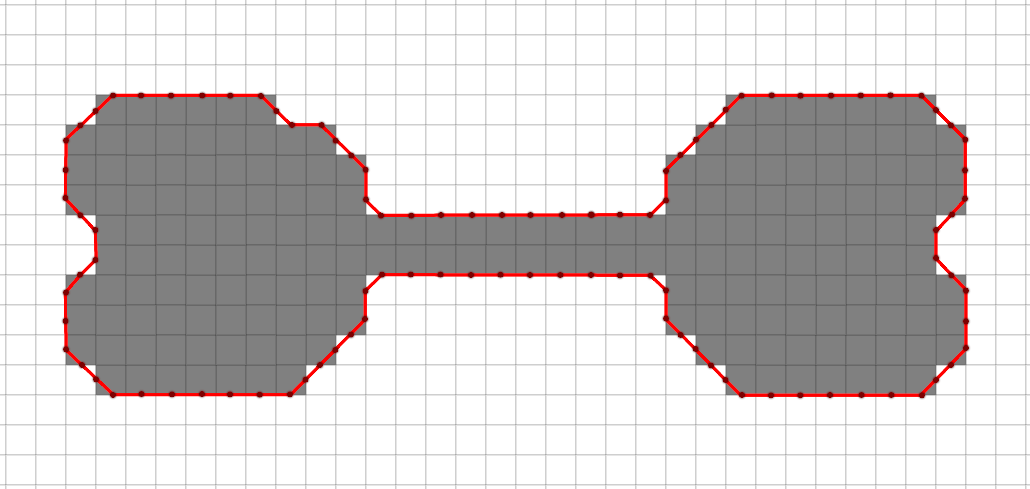
Результат 2D полигонализации

Поиск пути на полигональной сетке

В результате полигонализации изображения, мы возвращаемся к дискретному представлению поверхности в виде графа. Здесь проблему сглаживания можно решить с помощью вычисления геодезических расстояний [3],[4]. Геодезические расстояния являются наиболее точным способом измерения расстояний на поверхности. Они учитывают не только геометрическую длину пути, но и особенности самой поверхности. Эти различия можно увидеться на рисунке ниже.

Кратчайший путь на графе (слева) и с учетом геодезических расстояний (справа) [3]

В результате, геодезические расстояния на трехмерной полигональной модели выглядят следующим образом:

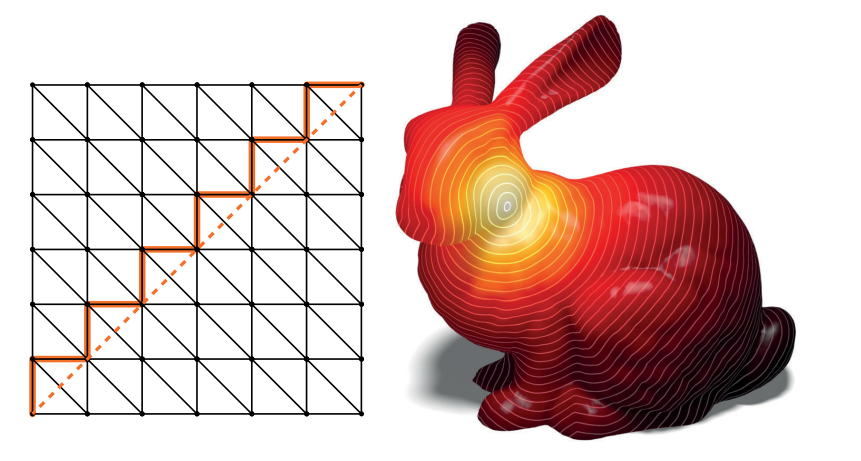
Заключение

Построение геодезического пути было достаточно для решения данной задачи, но все же не дает покоя мысль о том, что данную задачу, можно было бы решить без перехода к полигональной поверхности. В процессе, я наткнулся на книгу по функционально-воксельному моделированию [5], и работу по применению функционально-воксельного метода в решении задач поиска пути [6]. Но уже не было желания читать и разбирать эти работы, таким образом изучение данного вопроса представляется читателю.

Литература

Daniel, Kenny & Nash, Alex & Koenig, Sven & Felner, Ariel. (2014). Theta*: Any-Angle Path Planning on Grids. J. Artif. Intell. Res. (JAIR). 39. 10.1613/jair.2994.
Nash, Alex & Koenig, Sven & Tovey, Craig. (2010). Lazy Theta*: Any-Angle Path Planning and Path Length Analysis in 3D. Proceedings of the 3rd Annual Symposium on Combinatorial Search, SoCS 2010. 1.
Crane, Keenan & Livesu, Marco & Puppo, Enrico & Qin, Yipeng. (2020). A Survey of Algorithms for Geodesic Paths and Distances.
Crane, Keenan & Weischedel, Clarisse & Wardetzky, Max. (2017). The heat method for distance computation. Communications of the ACM. 60. 90–99. 10.1145/3131280.
Толок А.В. Функционально-воксельный метод в компьютерном моделировании
/ Под ред. акад. РАН С.Н. Васильева. — М.: ФИЗМАТЛИТ, 2016. 112 с. ISBN: 978–5–9221–1680–0.
Локтев М.А. Особенности применения функционально-воксельного моделирования в задачах поиска пути с препятствиями // Информационные технологии в проектировании и производстве. 2016. № 1. С. 45–49.