Поиск цикла Эйлера алгоритмом backtracking
Алгоритм поиска с возвратом является хоть и затратным, но зато достаточно универсальным методом. Связан он с перебором вершин графа. Возникает вопрос: можно ли интерпретировать ребра в качестве вершин? Вот эта идея и реализуется.
Код позволяет найти, с учетом стартовой вершины, цикл Эйлера или хотя бы его маршрут (полу-Эйлер). По сути, за вершину в такой интерпретации берется множество из двух соседних вершин. Реализовано в dict_to_setEdge. Что касается dfs, то это стандартная реализация обхода в глубину с возвратом.

рис. из интернета
# не Эйлер
G1 = {
1: [2, 3, 5],
2: [1, 4, 5],
3: [1, 4, 5],
4: [2, 3, 5],
5: [1, 2, 3, 4]
}
# полу-Эйлер
G2 = {
1: [2, 3, 5],
2: [1, 4, 5, 6],
3: [1, 4, 5],
4: [2, 3, 5, 6],
5: [1, 2, 3, 4],
6: [2, 4]
}
# Эйлер
G3 = {
1: [2, 3, 5, 7],
2: [1, 4, 5, 6],
3: [1, 4, 5, 7],
4: [2, 3, 5, 6],
5: [1, 2, 3, 4],
6: [2, 4],
7: [1, 3]
}
def dfs(g, v, path):
#print("path =", path)
if len(path)-1 == len(edgeSet):
return path
for w in g[v]:
if not {v, w} in path:
path.append({v, w})
newpath = dfs(g, w, path)
if newpath:
return newpath
path.pop()
def dict_to_setEdge(G):
s = []
for v in G:
for z in G[v]:
if not {v, z} in s:
s.append({v, z})
return s
v = [1, 2]
for i,g in enumerate([G1, G2, G3]):
edgeSet = dict_to_setEdge(g)
print("==== граф ===", i+1)
for s in v:
print(" для вершины =", s)
p = dfs(g, s, [{s, None}])
if not p:
print("Эйлер и полу-Эйлер не найдены")
elif len({s, None}.intersection(p[-1])):
print("Эйлер найден", p[1:])
else: print("Полу-Эйлер найден", p[1:])
print()
Теперь модифицируем формат данных так, чтобы была возможность обработки мульти-графов. Для этого, во-первых, добавим именованные ребра. Во-вторых, к двум смежным вершинам (3,7) добавим еще одно ребро (для G5) или еще два ребра (для G4). Соответственно, G4 Эйлеровым графом останется.
# Эйлер
G4 = {
1: [(2,1), (3,1), (5,1), (7,1)],
2: [(1,1), (4,1), (5,1), (6,1)],
3: [(1,1), (4,1), (5,1), (7,1), (7,2), (7,3)],
4: [(2,1), (3,1), (5,1), (6,1)],
5: [(1,1), (2,1), (3,1), (4,1)],
6: [(2,1), (4,1)],
7: [(1,1), (3,1), (3,2), (3,3)]
}
# не Эйлер
G5 = {
1: [(2,1), (3,1), (5,1), (7,1)],
2: [(1,1), (4,1), (5,1), (6,1)],
3: [(1,1), (4,1), (5,1), (7,1), (7,2)],
4: [(2,1), (3,1), (5,1), (6,1)],
5: [(1,1), (2,1), (3,1), (4,1)],
6: [(2,1), (4,1)],
7: [(1,1), (3,1), (3,2)]
}
def dfs(g, v, path):
#print("path =", path)
if len(path)-1 == len(edgeSet):
return path
for w in g[v]:
if not ({v, w[0]}, w[1]) in path:
path.append(({v, w[0]}, w[1]))
newpath = dfs(g, w[0], path)
if newpath:
return newpath
path.pop()
def dict_to_setEdge(G):
s = []
for v in G:
for z in G[v]:
if not ({v, z[0]}, z[1]) in s:
s.append(({v, z[0]}, z[1]))
return s
v = [1, 2]
for i,g in enumerate([G4, G5]):
edgeSet = dict_to_setEdge(g)
#print(edgeSet); input()
print("\n==== граф ===", i+1)
for s in v:
print("для вершины =", s)
p = dfs(g, s, [{s, None}])
if not p:
print("Эйлер и полу-Эйлер не найден")
elif len({s, None}.intersection(p[-1][0])):
print("Эйлер найден", p[1:])
else: print("Полу-Эйлер найден", p[1:])
print()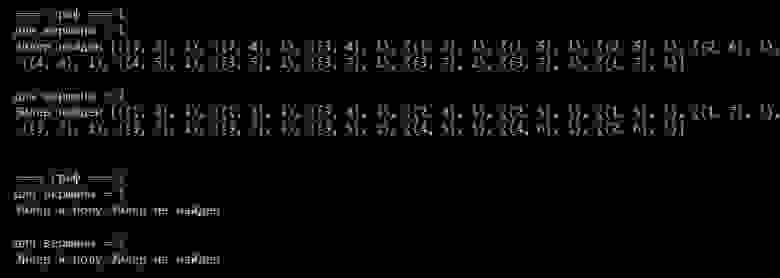
Вот и все.
