Поговорим про перформанс-анализ

Когда начинается разговор про перформанс-тестирование, то большинство программистов размышляет только о проведении замеров и сборе метрик, в то время как намного важнее задуматься об анализе собранных значений. Понять, как правильно использовать измеренные метрики и извлечь из них максимум пользы, — не такая уж и простая задача.
Сегодня мы обсудим основные задачи и сложности перформанс-анализа: поговорим о том, как изучать сырые данные и сводные метрики, применять статистические тесты, сравнивать перформансные распределения, писать перформансные тесты, анализировать историю замеров и выбирать правильные метрики. С этим нам поможет Андрей Акиньшин — ниже представлены видеозапись и расшифровка его доклада.
Доклад был сделан летом на нашей .NET-конференции DotNext. Заметим, что 2–5 декабря пройдет новый DotNext, где тему производительности тоже осветят — например, в докладе «Как легко измерить производительность CPU и паттерны аллокации памяти несколькими строками на C#».
Презентацию доклада Андрея можно посмотреть тут.
Далее — повествование от лица спикера.
Задачи перформанс-анализа
Давайте начнём с того, как выглядит типичный день обычного перформанс-инженера.

Порядок действий довольно простой. Нужно взять проблему, изучить её, придумать решение и реализовать его. Потом нужно взять следующую проблему, изучить её, придумать решение и реализовать его. И так от начала трекера и до заката.
Хотя, если подумать, то так выглядит типичный день не только для перформанс-инженеров, но и для многих других инженеров. Так вот, поговорим о том, как выбраться из порочного круга непрерывного решения внезапных проблем. Говорить будем в контексте производительности приложений, но многие идеи и подходы могут пригодиться в любой технической деятельности.
Тема перформанс-анализа очень большая, но в ней можно выделить четыре основных задачи:
- Анализ распределений. Он даёт ответ на вопрос о том, какова продолжительность некоторой операции. Увы, если мы N раз замерим один и тот же метод, то получим N разных значений. А как их агрегировать — не очень понятно. Часто можно услышать, что вроде бы брать среднее — плохо, брать медиану — плохо, брать любую другую метрику — тоже плохо.
- Сравнение бенчмарков. Вот есть у нас два варианта алгоритма, и нужно понять, какой из них быстрее. Но если начать мерить, то порой оказывается, что в половине случаев быстрее первый, а в другой половине — второй. Как в этом случае принять бизнес-решение о выборе правильного алгоритма для продакшна — тоже не очень понятно.
- Анализ истории. Гоняется, скажем, набор некоторых тестов на CI-сервере после каждого коммита. И вроде есть ощущение, что по этим данным мы можем обнаружить моменты, в которые всё стало работать медленнее. Но из-за шума и большого разброса значений логика обнаружения вызывает огромное количество трудностей.
- Написание перформанс-тестов. Это мечта многих разработчиков и тестировщиков — написать некоторую логику и сказать ей: не регрессируй по производительности. Если логика стала работать медленнее, то тест должен сразу упасть. А если не стала — то не должен. Звучит просто ровно до того момента, когда вы попытаетесь написать такой тест. У большинства моих знакомых первые 30 попыток оказываются неудачными, после чего они бросают это занятие.
Источники вдохновения
Сегодня я буду много рассказывать о различных подходах и алгоритмах для решения этих задач. Появились эти подходы не на пустом месте, а в результате многолетнего опыта работы над несколькими проектами.
Первый из них — BenchmarkDotNet. Это библиотека для точных и надёжных замеров перформанса .NET-приложений, которую я начал делать семь лет назад как маленький pet project. К сожалению, с ним случилось самое страшное, что вообще может случиться с опенсорс-проектом: он стал популярным. Сейчас у проекта тысячи пользователей и миллионы скачиваний.
А страшно это потому, что все эти пользователи постоянно пишут мне и задают разные вопросы. И самый популярный вопрос звучит так: «Ну, вот замерил я производительность, получил какие-то циферки, а дальше-то что делать?» И это очень хороший вопрос. Действительно, далеко не всегда понятно как анализировать результаты замеров.
Тогда я решил завести ещё один проект — Perfolizer. В нём я потихоньку собираю разные алгоритмы для перформанс-анализа, которые доступны в виде NuGet-пакета и в виде command line-тулов. Сначала пользователи радовались, но потом они начали задавать новый вопрос: «Ну, применил я эти алгоритмы, получил какие-то результаты, а дальше-то что делать?» И это тоже очень хороший вопрос, на который я попытаюсь вам ответить сегодня.
А ответ основан на опыте, который я получил в компании JetBrains, работая над проектом Rider. Это кросс-платформенная среда разработки для .NET на базе ReSharper и IntelliJ IDEA. Проект довольно большой: в нём несколько десятков миллионов строчек кода, и каждый день добавляются сотни новых коммитов. Производительность — это одна из главных фич, которая важна для наших пользователей. Увы, судьба складывается так, что у нас постоянно возникают перформанс-проблемы в самых неожиданных местах. Их нужно оперативно находить, изучать и побеждать. В ходе этой бесконечной борьбы появилось довольно много хороших подходов, которыми я сегодня поделюсь с вами. Давайте же отправимся в волшебную страну перформанс-анализа и разберёмся со всеми этими задачами.
План
— 1. Изучаем сырые данные
— 2. Изучаем сводные метрики
— 3. Применяем статические тесты
— 4. Сравниваем перформансные распределения
— 5. Анализируем историю замеров
— 6. Анализируем точки разладки
— 7. Пишем перформансные тесты
— 8. Допускаем ошибки
— 9. Читаем методическую литературу
— 10. Резюме
— 11. Титры
1. Изучаем сырые данные
И начнём мы с анализа сырых данных. Это отправная точка для многих перформанс-исследований: нужно глазами посмотреть на графики и понять, что там происходит. Давайте попробуем сделать это вместе.
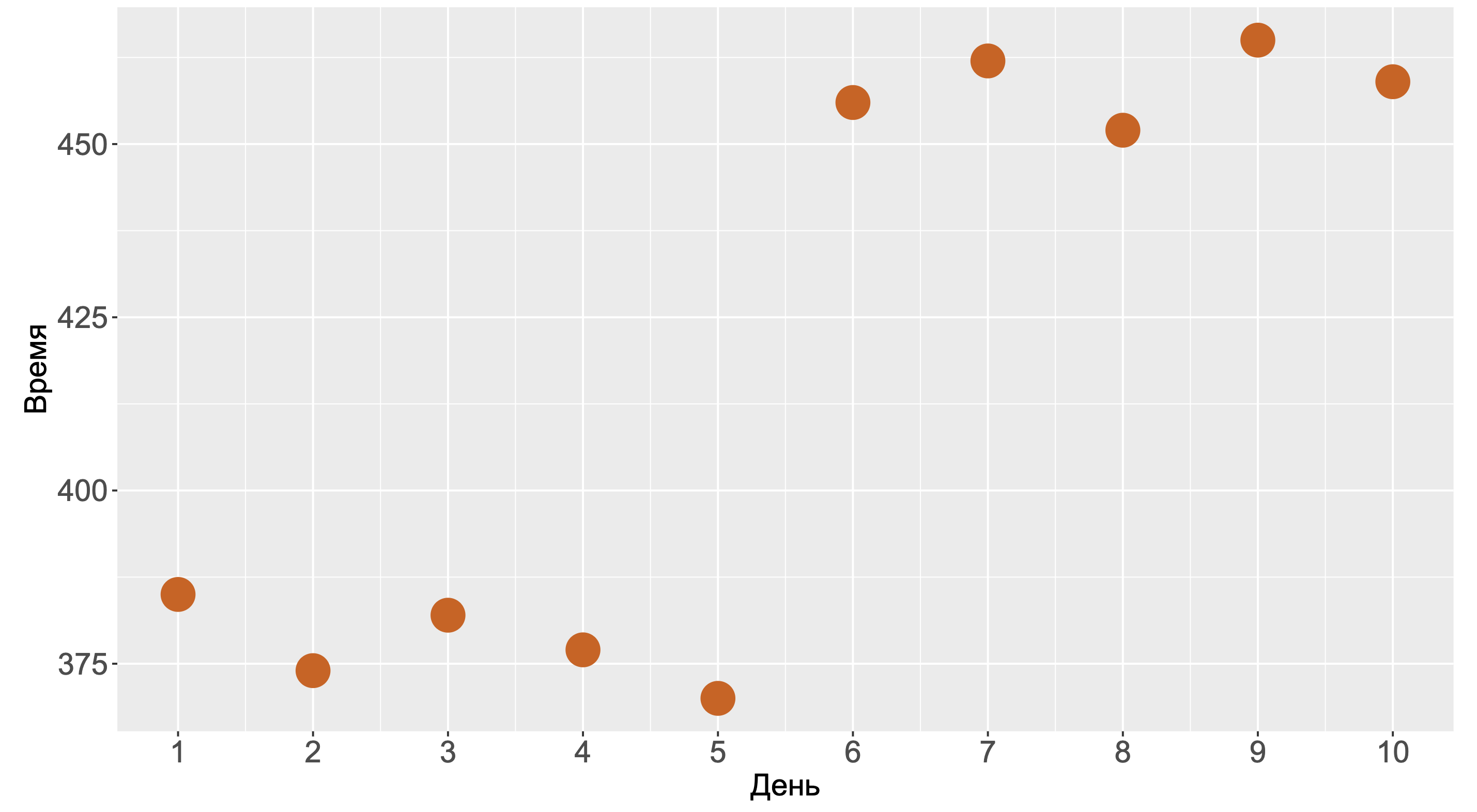
Посмотрите на этот график. За ним скрывается бенчмарк, который мы запускали в течение десяти дней. На каждый день приходится один-единственный замер. С одной стороны, график выглядит так, будто на шестой день у нас произошла деградация. С другой стороны, мы могли получить такую картинку и без деградаций, просто из-за того, что нам не повезло.
Давайте решим вот какую задачку. Допустим, у нас имеется десять тысяч тестов, каждый из которых запускался по разу в течении десяти дней. При этом исходный код никто не меняет, тесты всё время замеряют одно и тоже. Какова вероятность получить хотя бы один подобный график, на котором последние пять замеров больше, чем первые пять замеров?
Для простоты предположим, что форма распределения нам известна и она бимодальна. Какова вероятность того, что первые пять замеров будут из первой моды, а последние пять замеров — из второй?
Правильный ответ: 2–10 или 0,0009765625. Вроде выглядит как довольно маленькая вероятность, но давайте вспомним, что у нас десять тысяч тестов. Несложно подсчитать вероятность того, что хотя бы на одном тесте мы получим такую псевдо-деградацию. Получится практически 100%.
В качестве упражнения попробуйте обобщить эту формулу на случай произвольного распределения и посмотрите, что получится там. А мы продолжим работать с нашей моделью и посмотрим на зависимость вероятности от количества тестов.
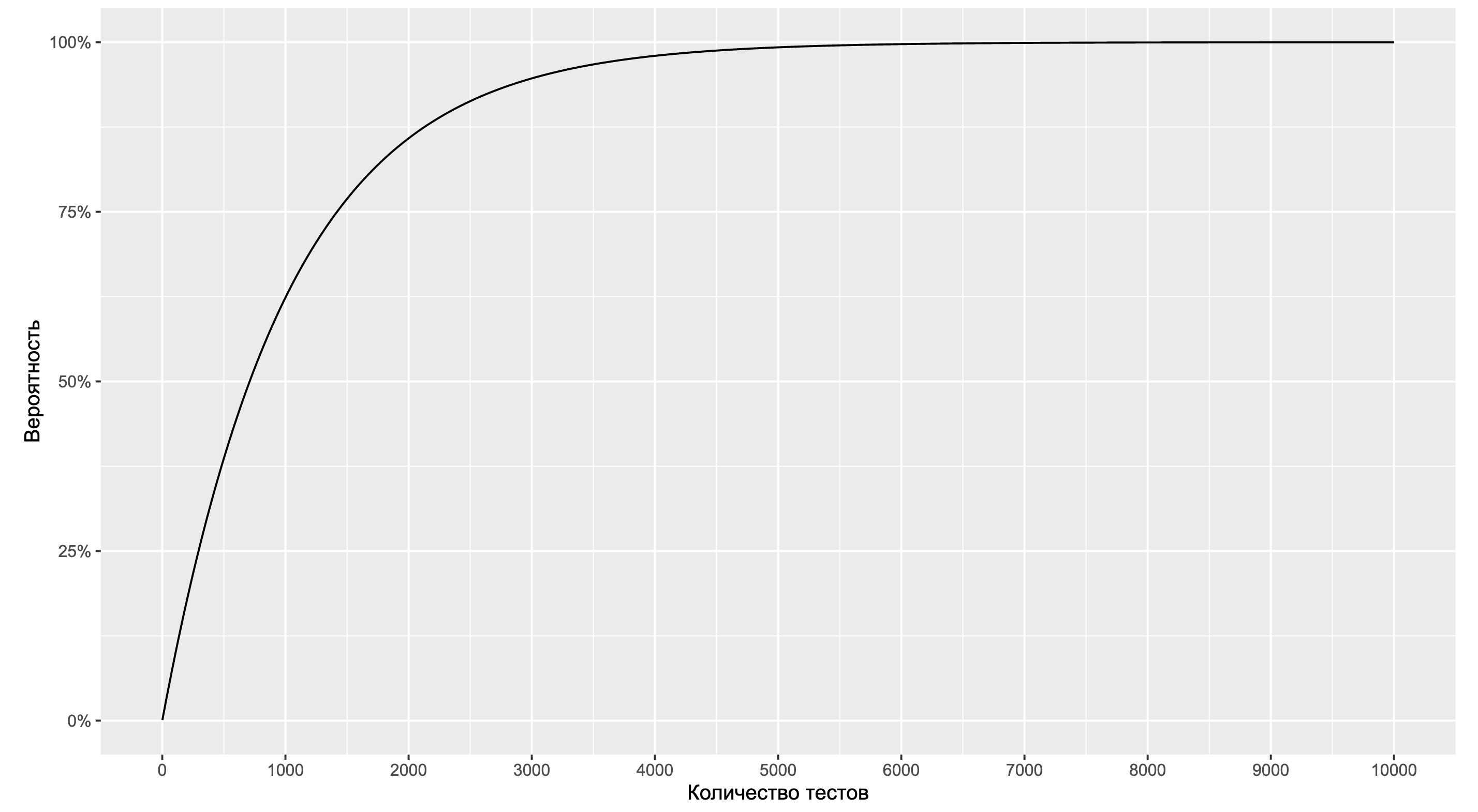
Как можно видеть, мы приближаемся к 100% уже на 5000 тестов. А это довольно маленькое количество тестов по энтерпрайзным меркам. Если же мы обобщим форму распределения и начнём искать другие типы ситуаций с подозрительными графиками, то мы имеем все шансы их найти уже на 1000 тестов. Если систематически смотреть на эти графики, то скорее всего мы быстро наткнёмся на подобные картинки. И тут начинаются проблемы, так как наш мозг очень любит искать паттерны.
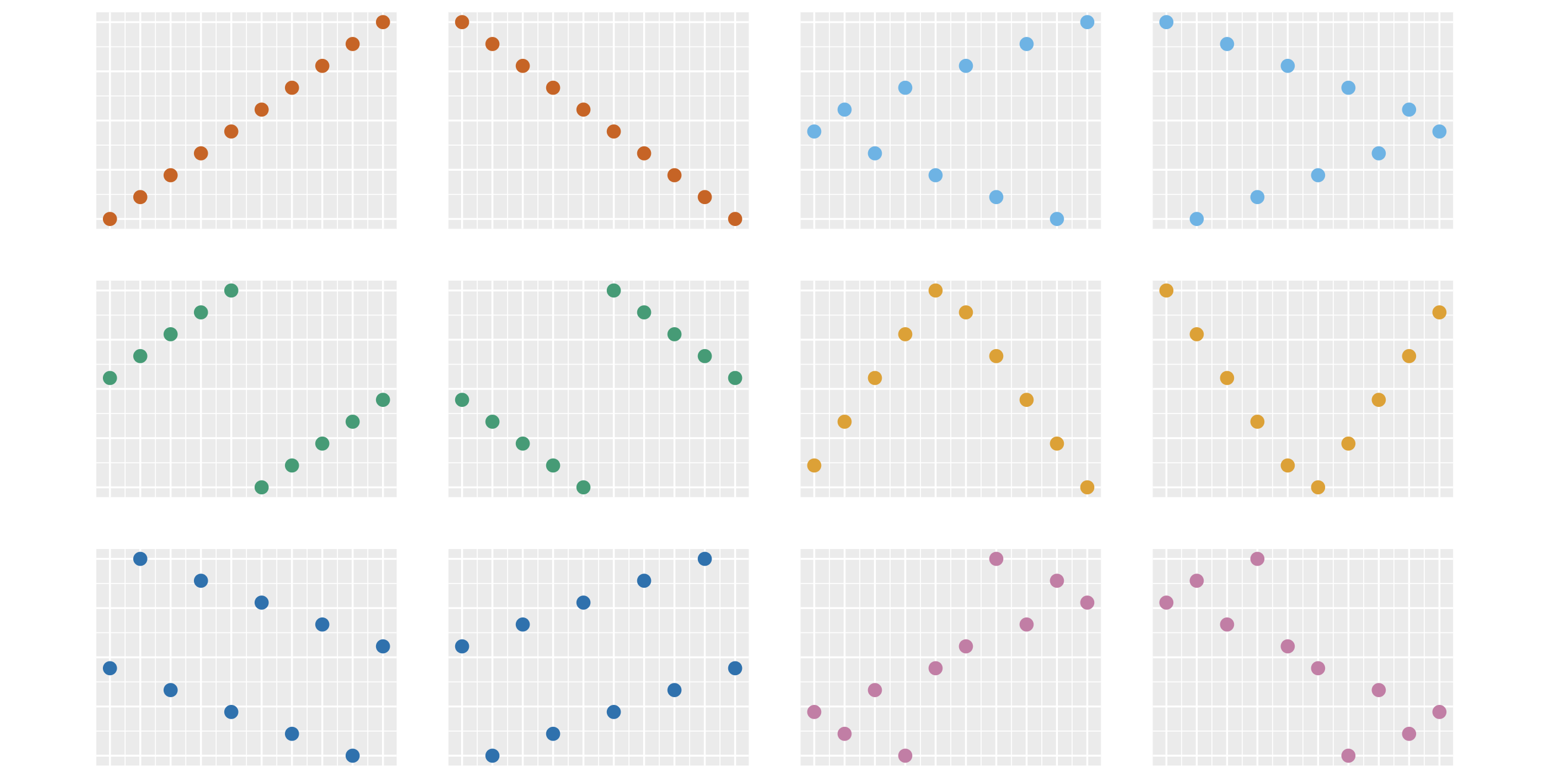
Сейчас вы видите 12 разных картинок. На каждой изображены 10 точек. Набор ординат точек на всех картинках одинаковый, отличается только их порядок. При большом количестве тестов велика вероятность получить любую из этих картинок совершенно случайно. Однако у нашего мозга есть удивительная способность видеть структуру и взаимосвязи в случайных и бессмысленных данных. По научному такой феномен называется апофения.
Даже на полностью рандомных данных человек всегда найдёт несколько ситуаций, когда захочется сказать: «Мы никак не могли получить такую картинку случайно, тут явно есть закономерность!» На этом свойстве нашего мозга базируется большое количество разных когнитивных искажений. Последствия бывают самые разные.
От веры в то, что танец с бубном поможет ускорить программу, до десятков бесполезных часов, которые проведены в поисках проблемы, которой на самом деле нет.
Кто лучше всех разбирается в перформанс-анализе?
На эту тему написано большое количество статей, но я решил для верности провести собственный эксперимент. В течение долгих недель я методично изучал разные перформанс-графики и пытался отгадать ситуации, в которых у нас есть проблемы.
В какой-то момент я решил начать записывать, насколько хорошо у меня получается. Процент успешных угадываний составил 20–30%. Это не так уж и плохо, лучше, чем у многих моих коллег.
Но я задался вопросом: «Можно ли угадывать ещё лучше?» Тогда я сделал из этих графиков набор задачек, в которых нужно было найти деградации. Ответ можно было дать автоматически, нажимая клавиши на клавиатуре. Я пошёл с этим набором к начальнику нашего .NET-отдела и попросил прорешать задачки… его кошку Осю. Сначала Ося восприняла эту идею без особого энтузиазма. Но вскоре её удалось усадить за клавиатуру, чтобы она нажимала на клавиши и давала ответы на задачки. Процент угадываний получился 45–55%.

Таким образом, Ося — намного более квалифицированный интуитивный перформанс-инженер, чем я. Увы, работать у нас фултайм Ося не захотела. К счастью, её логику принятия решений удалось аппроксимировать монеткой. Орёл — есть деградация, решка — нет деградации. Такой подход позволяет значительно улучшить качество анализа.
Общий вывод: сырые данные контринтуитивны и обманчивы. Даже если у вас большой опыт разбора всяких графиков, интуиция может создавать большое количество трудностей. И можно было бы продолжать пользоваться монеткой, но монеток на все расследования не напасёшься. Да и вручную смотреть на все эти графики довольно утомительно. Хочется иметь более доступный, надёжный и автоматизированный инструмент.
2. Изучаем сводные метрики
В такие моменты программисты начинают рассуждать о том, что нужно как-то агрегировать наши данные. Мол, надо подсчитать какие-то сводные метрики, засунуть их в умную формулу, и всё сразу станет хорошо.
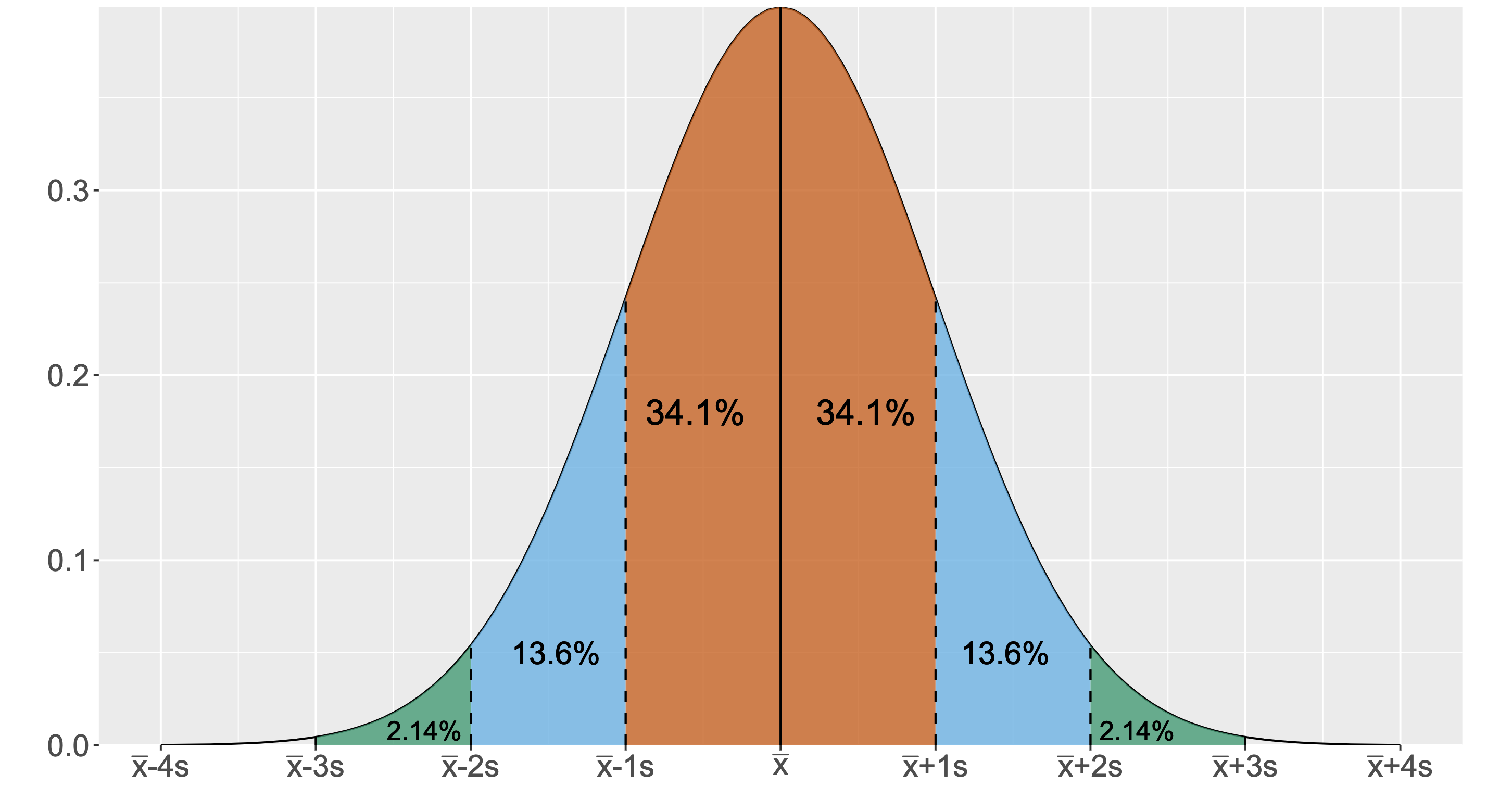
При работе с этими метриками в голове часто возникает картинка нормального распределения. Скорее всего, вы видели подобную картинку в учебниках по матстатистике. Однако сомневаюсь, что встречали нормальное распределение в реальной жизни.
Нужно признать, что нормальное распределение действительно возникает в некоторых предметных областях при определённых математических построениях. Но на сырых перформансных данных вероятность встретить идеальное нормальное распределение практически нулевая. Поэтому дальше мы будем полагать, что условие нормальности не выполняется. Распределение может иметь сколь угодно странную форму. Но, увы, людям инстинктивно хочется использовать нормальное распределение в качестве ментальной модели. Его проще всего себе представить. Давайте проведём эксперимент.

Посмотрите на эту таблицу и постарайтесь сходу сказать, какой из двух методов быстрее. Большинство людей смотрят только на среднее значение и игнорируют остальные метрики, так как с ними довольно сложно работать.
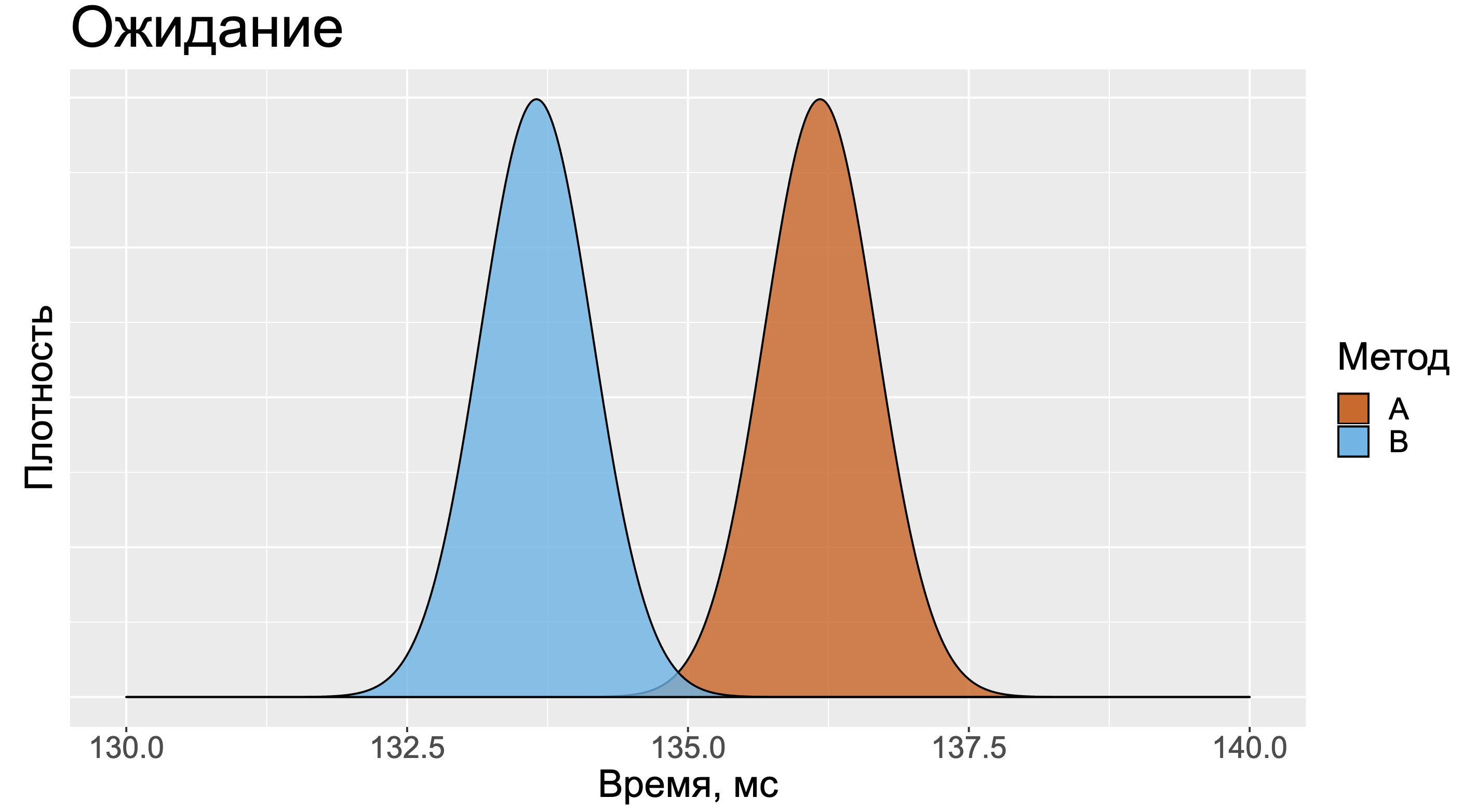
В данном случае хочется представить два примерно одинаковых нормальных распределения. Распределение для метода А будет немного правее, так как среднее значение замеров у него больше.
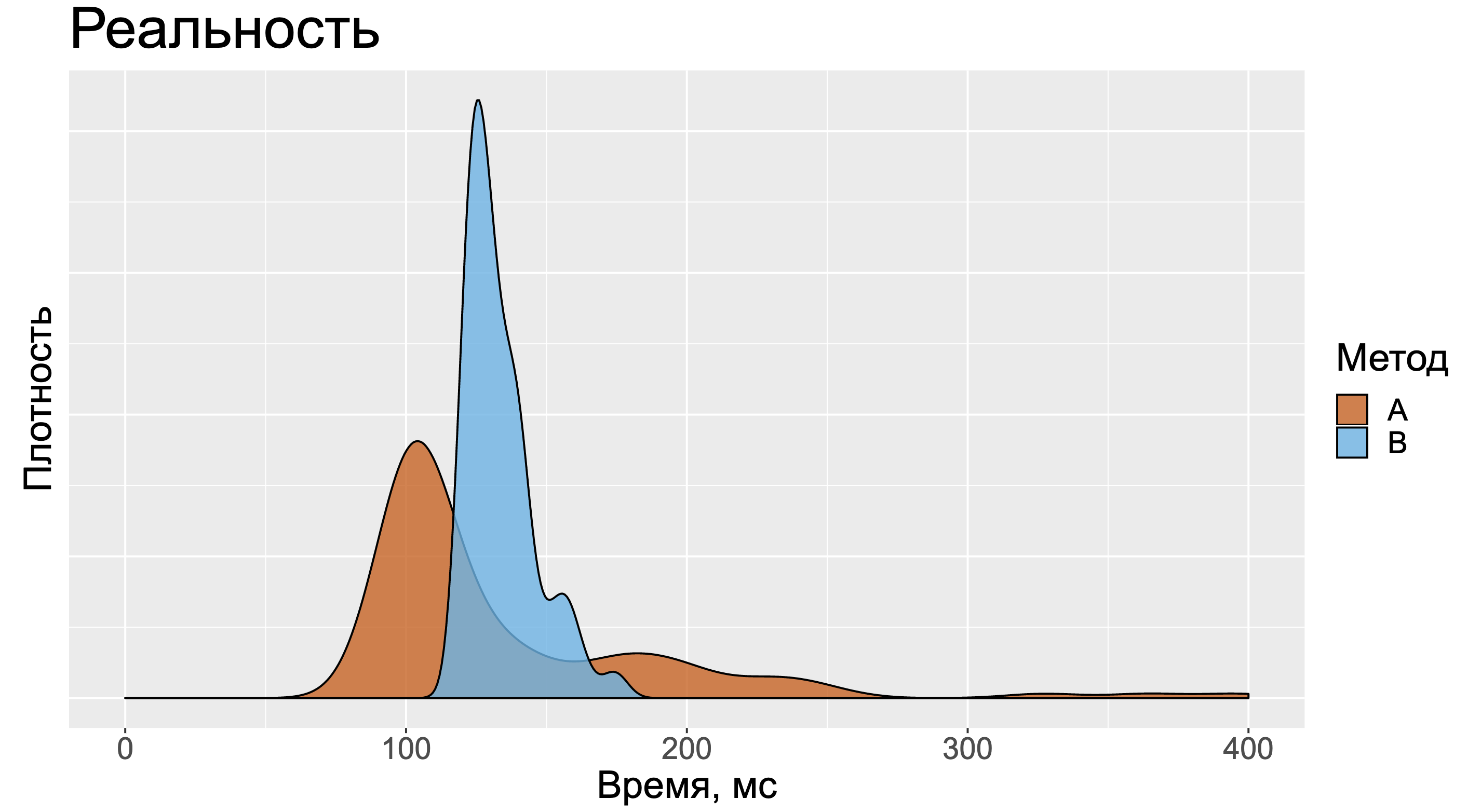
Но в реальности картинка может оказаться более сложной. Для методов А и B нельзя сказать кто быстрее. Когда-то быстрее А, когда-то быстрее B. И вроде бы большое значение стандартного отклонения должно было нас немного насторожить.
А тот факт, что медиана замеров метода А намного меньше медианы замеров метода B, должен был бы нас взволновать ещё сильнее.
Увы, в реальной жизни появляется привычка игнорировать дополнительные метрики. Особенно, если вы изучаете большое количество сводных таблиц с результатами бенчмарков. Слишком уж напряжно смотреть сразу на дюжину разных метрик, удерживать их в голове и пытаться сопоставить их друг с другом. Эффект обманчивости сводных метрик хорошо описан в научной литературе.
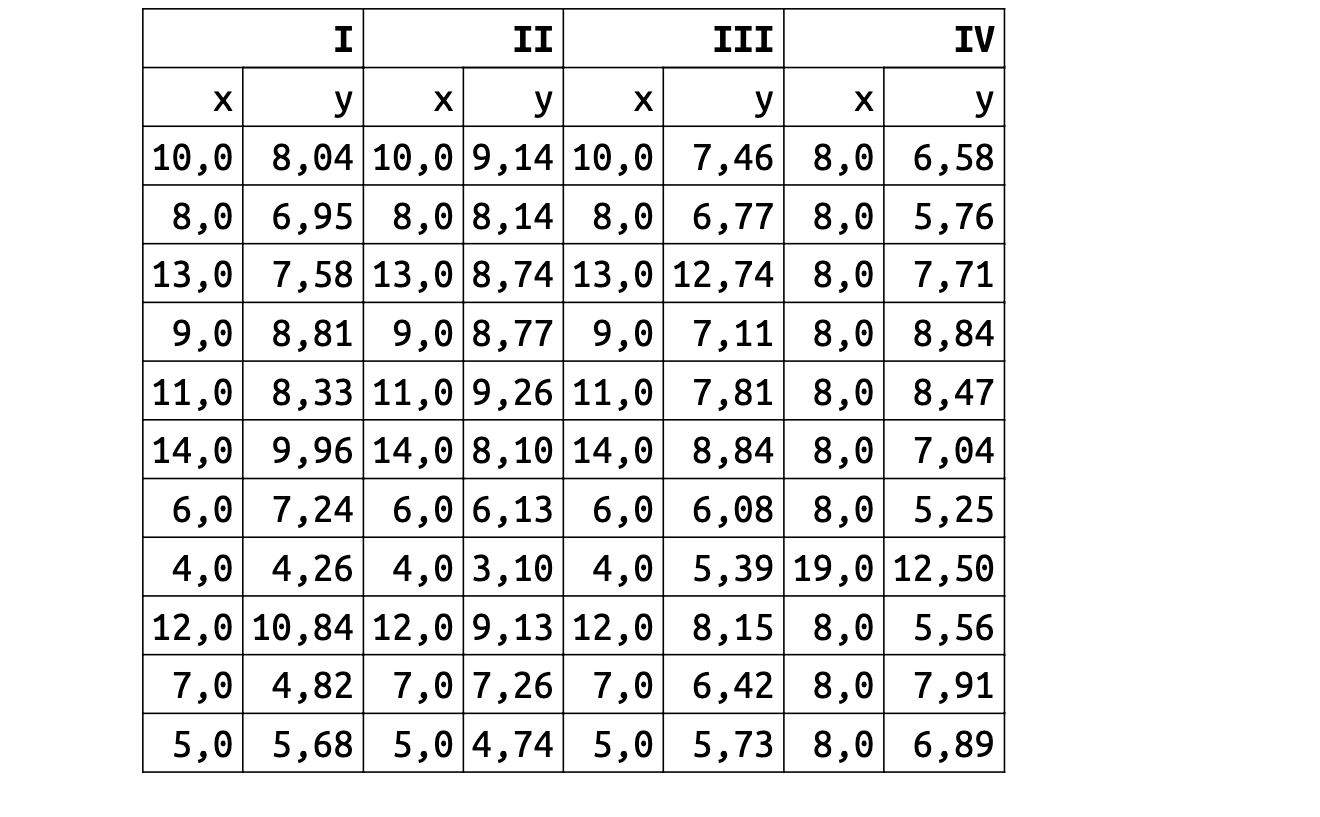
Одним из классических примеров подобной проблемы является квартет Энскомба 1973 года. Он состоит из четырёх наборов данных, в каждом из которых есть 11 пар значений x и y. Анализировать подобные сырые данные глазами тяжко. Поэтому возникает желание посмотреть на метрики.
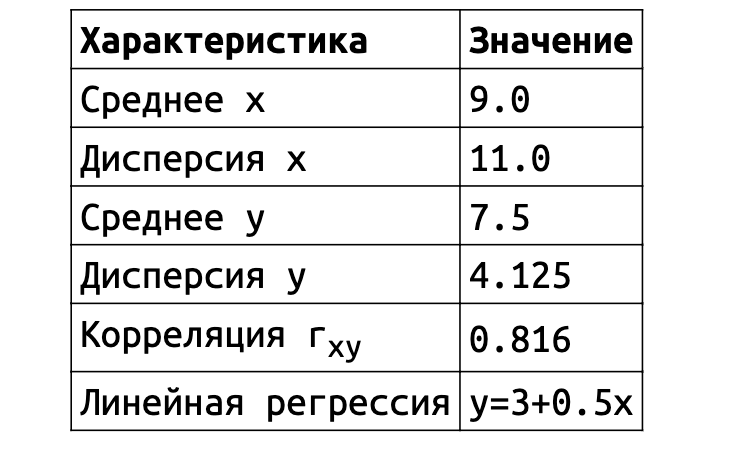
И тут начинается самое интересное. Значения средних, дисперсии, корреляции и формулы линейной регрессии оказываются практически одинаковыми для всех наборов данных.
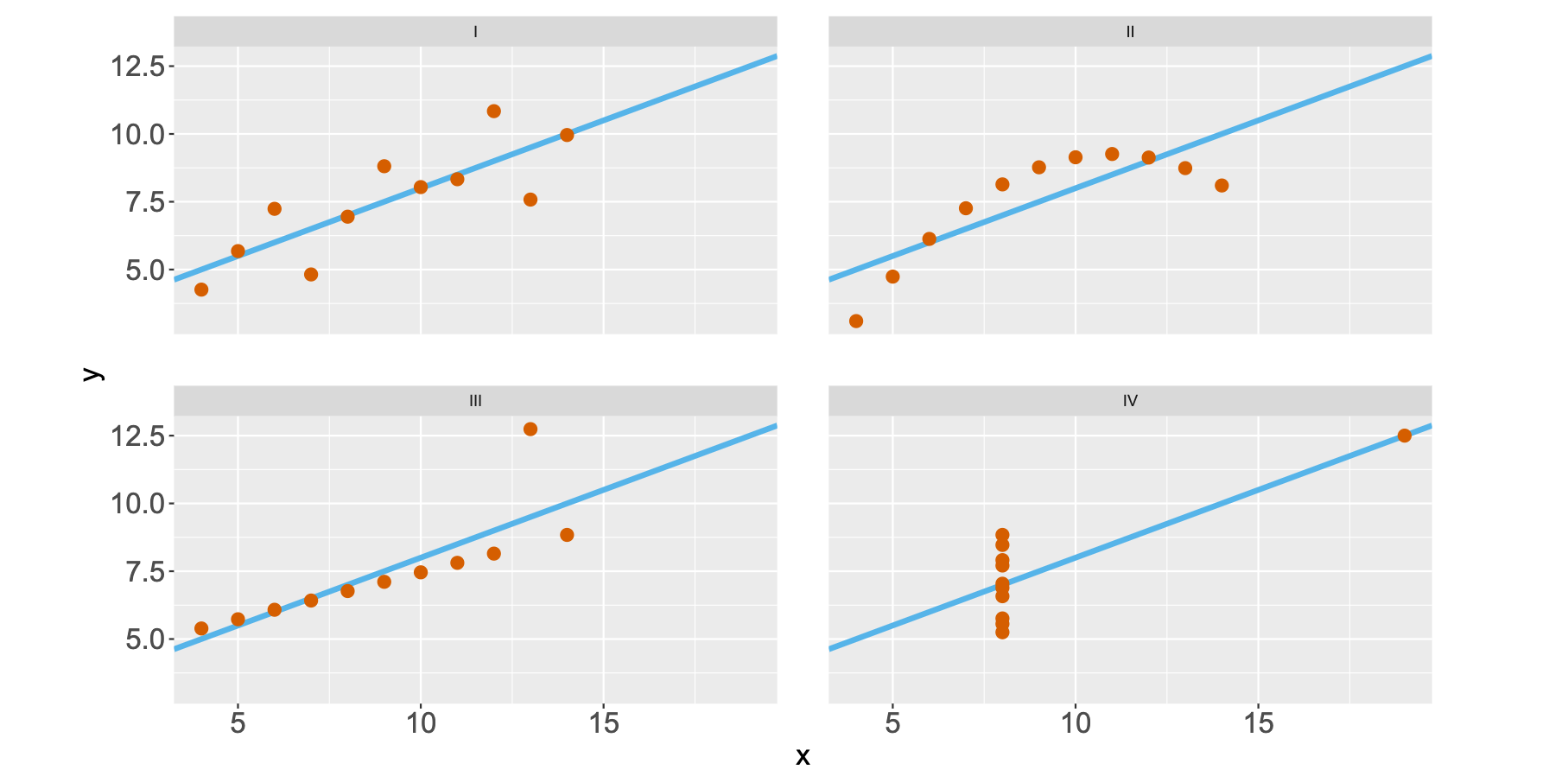
Однако форма этих данных абсолютно разная. Классические метрики скрывают от нас эту информацию. Даже если вы очень круто разбираетесь в матстатистике, вы не сможете обнаружить разницу между наборами данных только по метрикам. Просто потому, что такова их природа.

Из более свежих работ хочется отметить статью 2017 года «Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing», в которой пара канадских учёных нарисовала очаровательный набор разных картинок с одинаковыми значениями средних, дисперсий и корреляций.
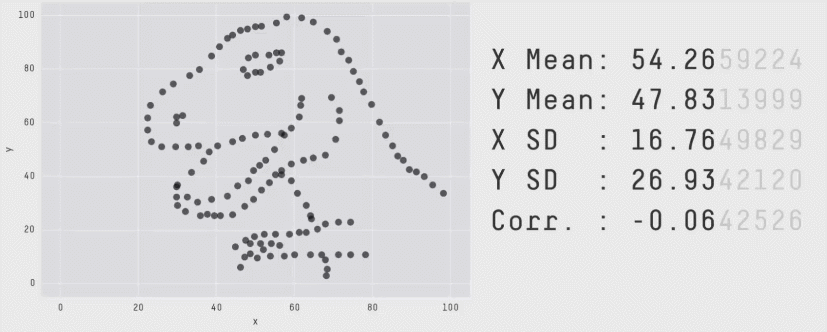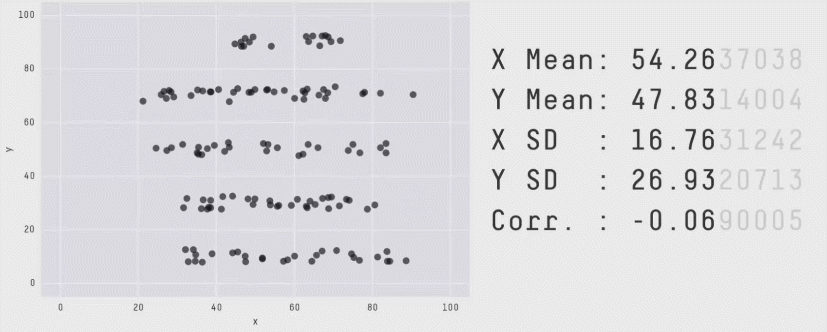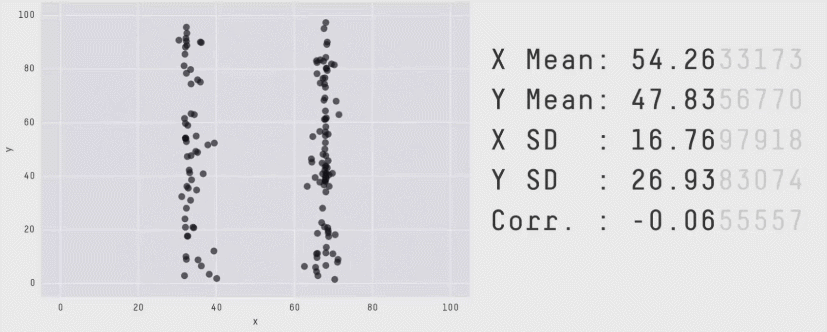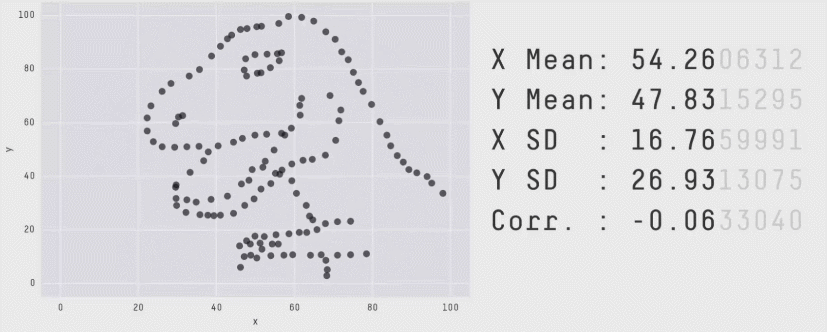
Ситуация аналогична квартету Энскомба: сводные метрики совпадают, но форма данных кардинально различается. И это грустно, так как вся классическая статистика построена на подсчёте каких-то странных метрик и попытках извлечь из них полезную информацию. Попытки победить в подобной угадайке могут обернуться провалом. Хочется создать подход, в котором статистические отчёты не будут нас обманывать столь подлым способом.
Статистика должна быть дружелюбной
К счастью, у нас есть компьютеры, с помощью которых мы можем сделать статистику более дружелюбной. Сейчас я покажу вам один из способов, который можно эффективно использовать на практике.
Основная идея в том, что мы будем описывать распределения с помощью интервалов, в которые попадает основная масса значений. Ведь именно это нас на самом деле интересует на первом этапе перформанс-исследования. Нам хочется примерно узнать сколько времени занимает тот или иной метод. Ответ «примерно 100–200 мс» зачастую нас вполне устроит.
Обычно мы пытаемся сами домыслить такой интервал по среднему и дисперсии, используя нормальное распределение в качестве ментальной модели. Почему бы не подсчитать такой интервал сразу? Но тут истинные математики возмутятся: «Как же мы будем сравнивать распределения без классических метрик? А что, если у нас есть большие выбросы?» Это может быть для нас важно, но эта информация в табличке отсутствует.
К счастью, обладая базовыми навыками программирования, можно легко обнаружить такие ситуации и отобразить эту информацию в табличке.
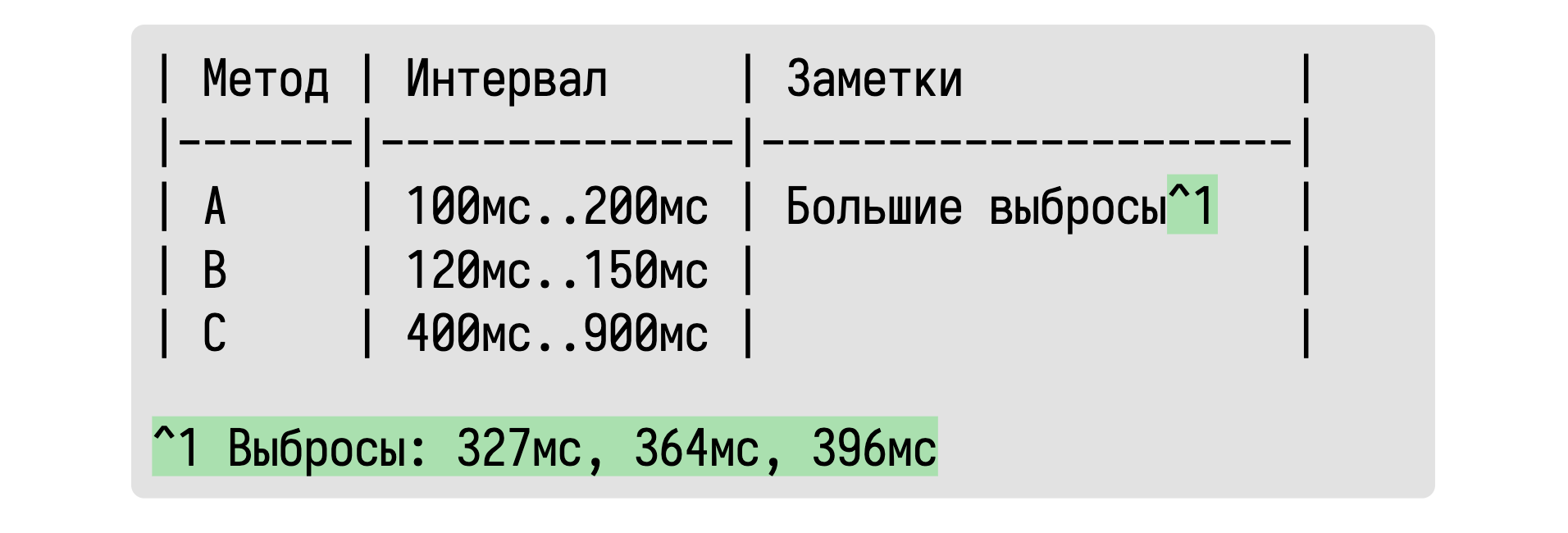
Если нас волнуют конкретные значения выбросов, то мы их можем также выписать. А что, спросите вы, если какой-то интервал оказался очень неточным из-за маленького размера выборки?
Про это тоже можно написать.
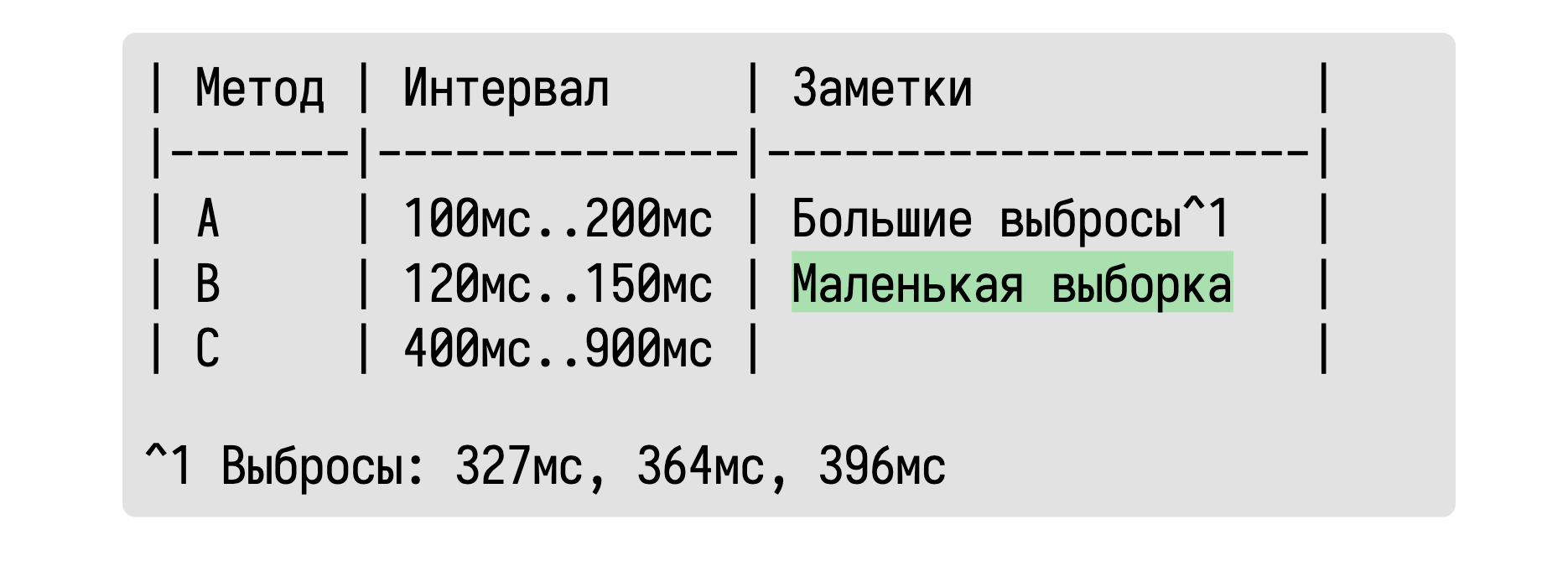
Если выборка слишком мала для получения достоверного результата, то можно просто это указать.

А что, спросите вы, если у нас распределение мультимодальное? Мы не сможем об этом узнать по такой табличке!
Мультимодальность тоже отлично обнаруживается.
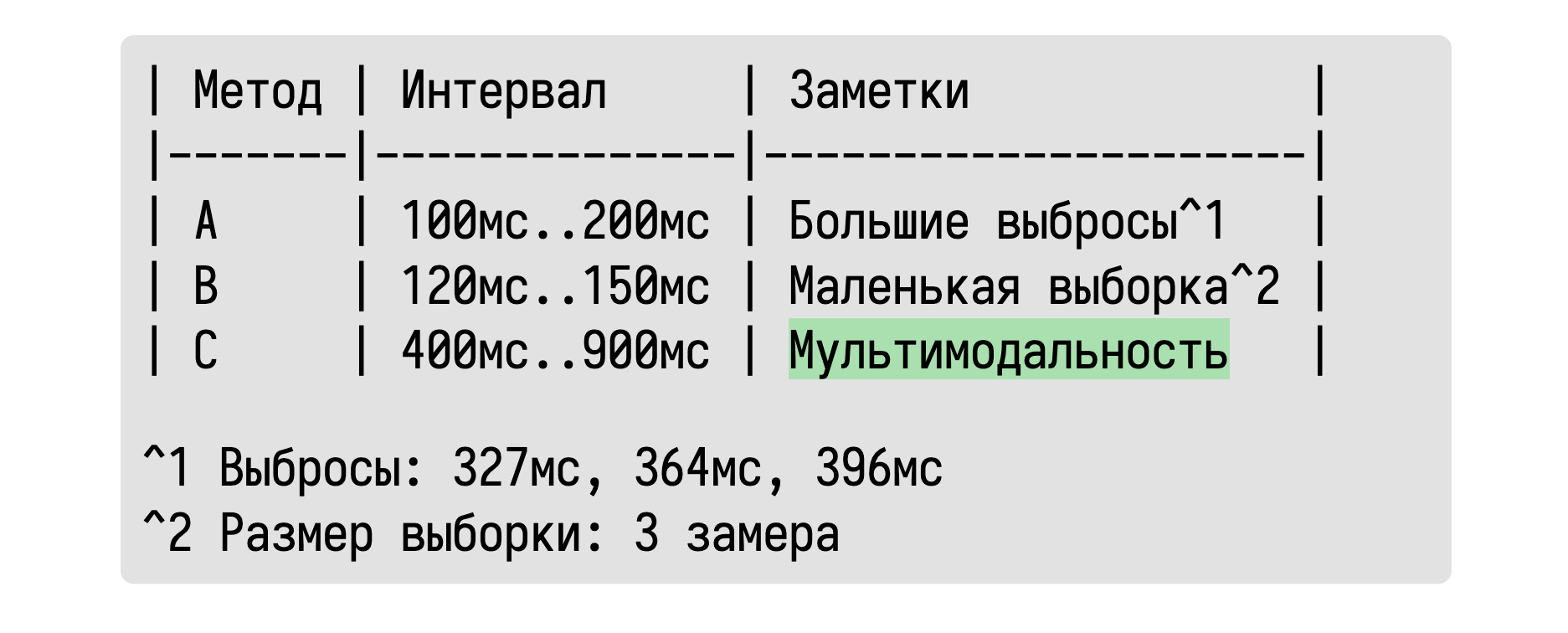
А если внутри нашего интервала существуют два или более подынтервалов, которые содержат основную массу значений, то давайте просто напишем об этом.
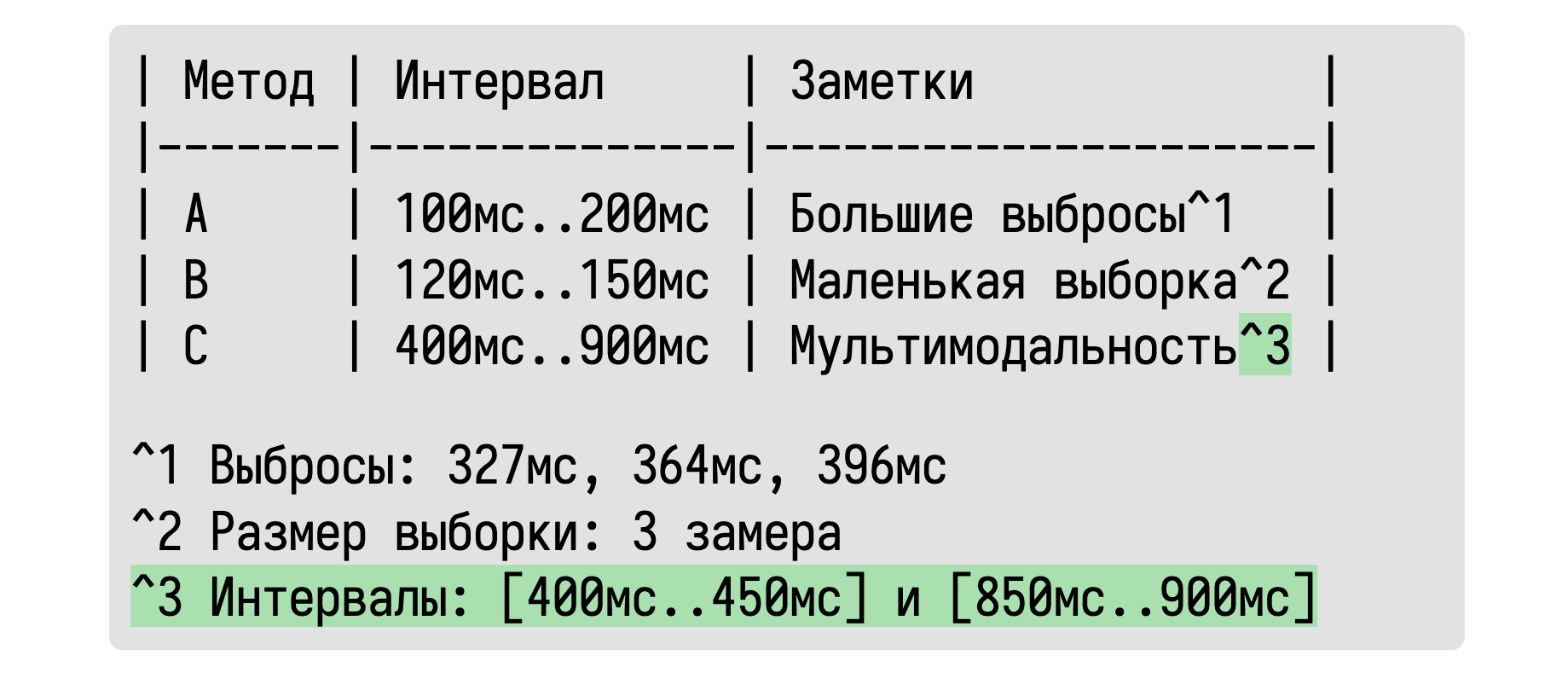
В классических статистических подходах мы должны угадывать подобные эффекты по непонятным для многих значениям дисперсии, стандартных ошибок, квантилей и прочих не особо легко интерпретируемых метрик. Вместо этого мы можем обнаружить все эти эффекты автоматически и вывести предупреждение о них только в тех случаях, когда это важно.
Источники шума и модальности
Необходимо также хорошо понимать, откуда берутся подобные распределения.
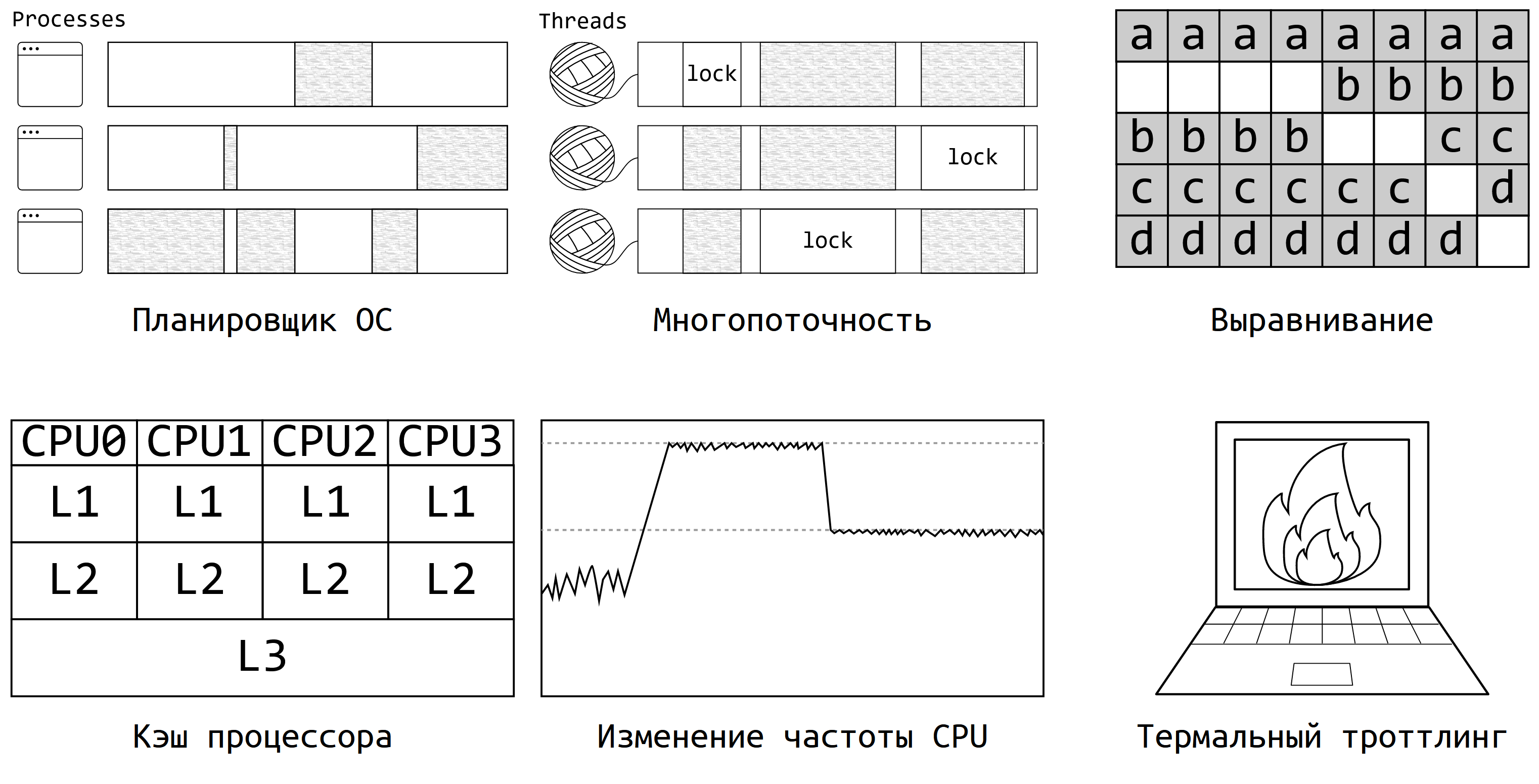
Программы исполняются в довольно сложных окружениях, где много разных факторов могут повлиять на ваши замеры. Вот основные источники:
Планировщик операционной системы: он сам решает, когда будет исполняться ваш бенчмарк и как будет делиться ресурсами с другими процессами.
Многопоточность: как только в программе появляется несколько потоков и хотя бы одна блокировка, программа вовсе становится недетерминированной. Из-за этого может появляться и мультимодальность, и очень большой разброс значений.
Выравнивание кода и данных: производительность может очень сильно зависеть от того, в какие области оперативной оперативной памяти вы попали.
Кэш процессора — ещё один заклятый враг любого перформанс-инженера. От его состояния производительность многих алгоритмов может скакать в несколько раз.
Изменение частоты процессора: современные компьютеры могут динамически менять частоту CPU по собственному усмотрению.
Термальный троттлинг — мой любимый пример на эту тему. Идея проста: если ваш любимый ноутбук перегрелся, то частота процессора может заметно упасть, чтобы вашим коленкам было не так горячо.
Я очень люблю рассказывать про то, как термальный троттлинг легко можно пронаблюдать в домашних условиях.
Давайте возьмём макбук и поместим его в два разных физических окружения. В первом случае он будет лежать в морозилке, а во втором будет завёрнут в одеялко вблизи керамического тепловентилятора. С помощью тепловизора можно убедиться в значительной разнице между температурами ноутбука в каждом из случаев. В морозилке мне удалось довольно легко удержать частоту на уровне 3,5 ГГц.
Запустив любой CPU-bound бенчмарк можно получить набор эталонных замеров. В одеялке же макбук быстро начинает перегреваться и скидывает частоту до базовых 2,5 ГГц.
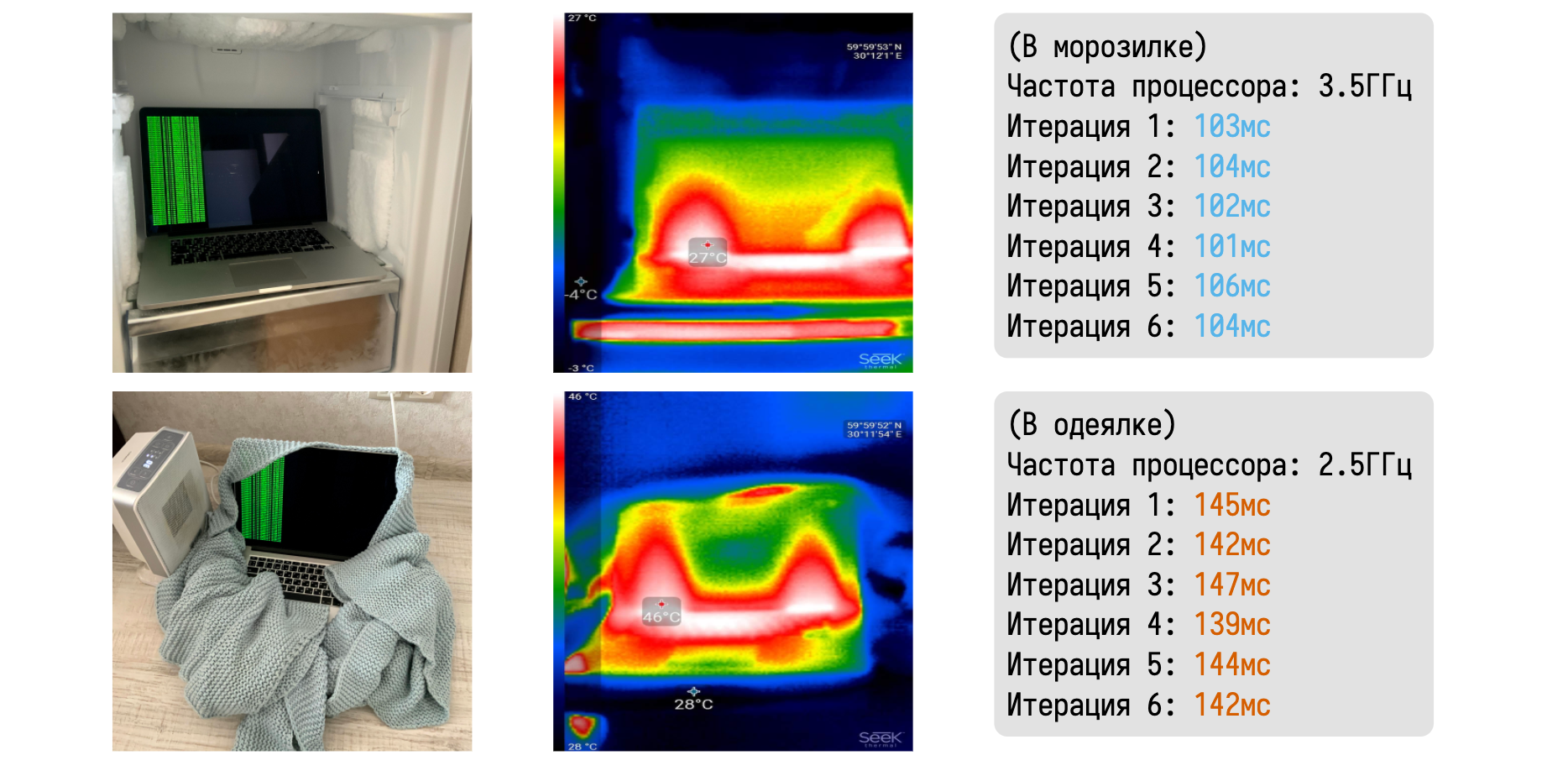
Результаты нашего бенчмарка сразу начинают драматически деградировать. Знание таких феноменов очень помогает при анализе значений замеров. На всех наших перформанс-агентах мы всегда записываем температуру процессора до и после бенчмарка. При возникновения троттлинга в логи пишется жирное предупреждение о недостоверности результатов. Подобные автоматические проверки хорошо дополняют дружелюбную сводную таблицу, показывая не только наличие странных феноменов в распределениях, но и их возможные причины.
Можно очень долго рассказывать о конкретных анализах и проверках, но мне хочется, чтобы вы запомнили основную идею: статистика может быть дружелюбной. Более того, она должна быть дружелюбной.
Вместо того, чтобы играть в угадайку при анализе обманчивых сводных метрик, можно сразу выводить те факты, которые мы хотим знать о наших замерах. С помощью этого мы легко можем решить нашу первую-перфоманс задачу по анализу распределений.
3. Применяем статистические тесты
Теперь можно перейти второй задаче по сравнению двух распределений. Скажем, есть у нас две версии алгоритма, нужно понять, есть ли между ними значительная разница в производительности.
Если вы погуглите на эту тему, то быстро наткнётесь на советы по использованию тестов на статистическую значимость. Ну что ж, давайте попробуем пойти этим путём, который довольно распространён в современном мире. Прежде всего, взглянем на типичную деградацию, которую нам хотелось бы уметь обнаруживать.
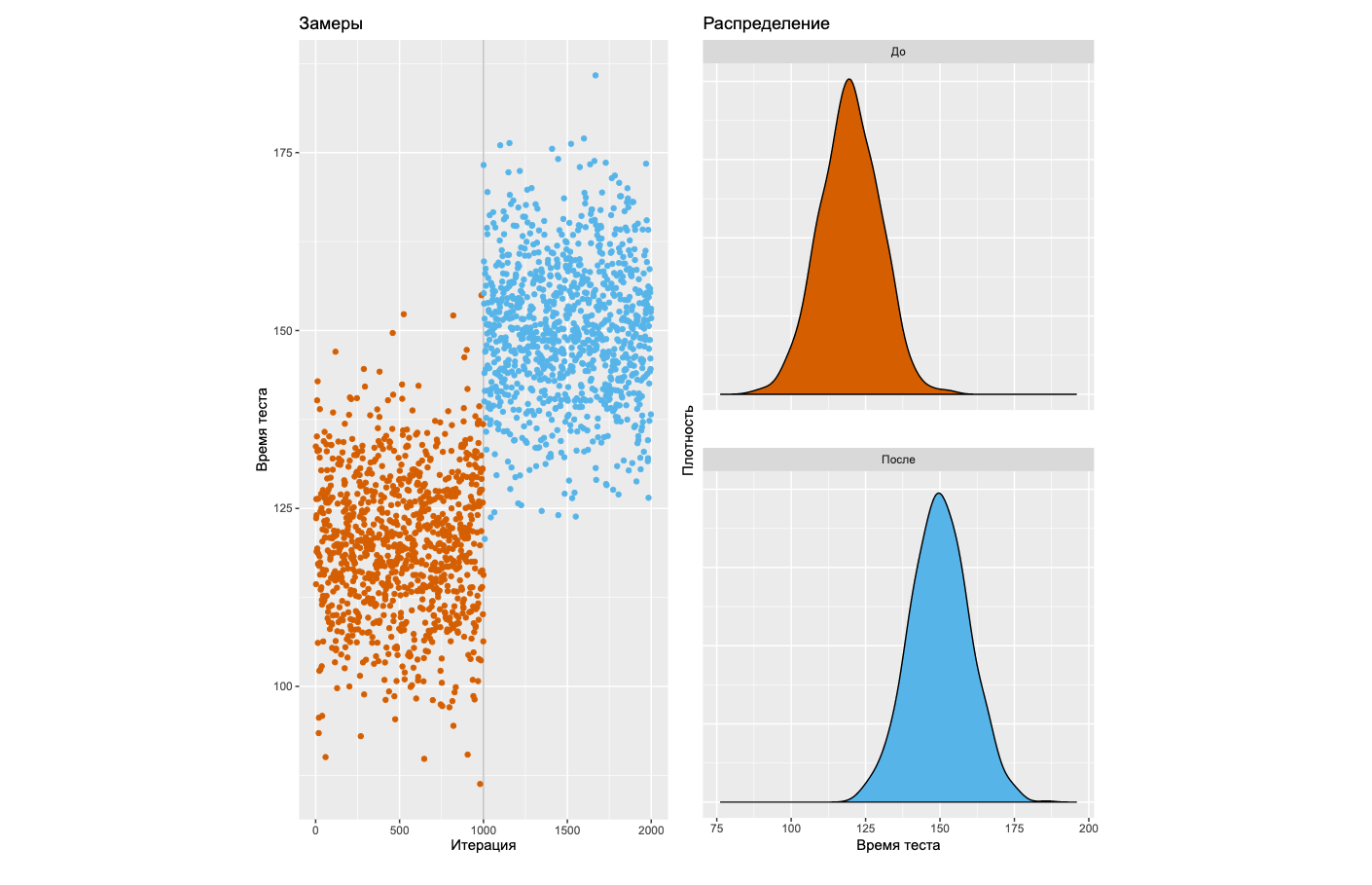
Слева вы видите график замеров некоторого бенчмарка на 2000 итераций. Детектор паттернов в вашем мозге мгновенно говорит, что после тысячной итерации произошла явная деградация. Справа можно посмотреть на плотности распределений до и после этого загадочного момента. Давайте научимся детектировать подобные ситуации с помощью статистических тестов!
Тут мы встречаем первую проблему: разных тестов очень много. Какой из них использовать — не очень понятно. Но давайте предположим, что мы выбрали какой-то тест. Неважно какой, они все работают примерно по одной схеме.
Прежде всего, нам нужно сформулировать так называемые статистические гипотезы. Обычно их две. Первая называется нулевой гипотезой: она будет нам говорить о том, что у нас нет деградации. Вторая называется альтернативной гипотезой: она говорит нам о том, что у нас есть деградация. Как по мне, термины ужасные — в современном мире такой нейминг никогда бы не прошёл code review.
Забавно, что термин «альтернативные гипотезы» придумали Нейман и Пирсон в 1933 году, но термин «нулевая гипотеза» им не особо нравился. Его придумал Фишер спустя два года, но идея использования альтернативных гипотез ему не очень нравилась.
В общем, имеющееся именование — это исторический курьёз, который магически распространился по научной литературе. И теперь это легаси с нами навсегда.
В результате применения статистических тестов обычно получается магическая метрика под названием p-value. Мало кто понимает, что она означает, но основная масса пользователей статистических тестов научились её использовать.
Если p-value оказалось меньше некоторой константы α, то мы говорим об отвергании нулевой гипотезы. Из такого утверждения хочется сделать вывод о том, что у нас есть деградация, но это далеко не всегда так.
Если же p-value оказалось больше магической константы α, то говорят, что «нельзя отвергнуть нулевую гипотезу». Тут начинаются большие сложности с интерпретацией, а смысл фразы остаётся для многих загадкой. Путём сложной цепочки логических выводов люди приходят к тому, что, наверное, это означает, что деградации всё-таки нет. Однако на самом деле это означает, что чёрт его знает, есть ли у нас деградация или нет — не совсем тот результат, который мы хотели бы получить. Но давайте продолжим вспоминать матчасть.
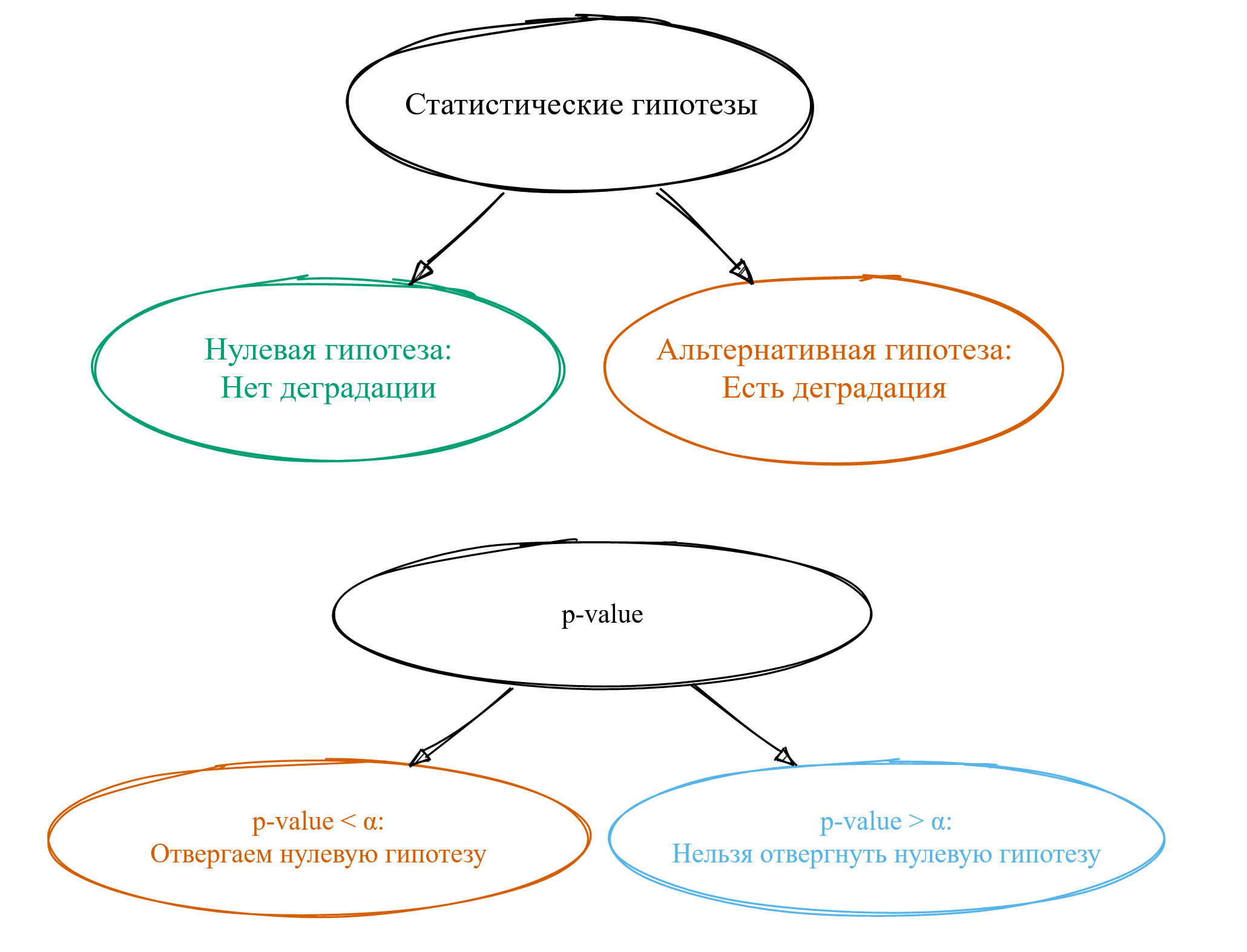
Статистические ошибки
Давайте взглянем на самые главные ошибки, которые можно допустить:
- Ошибка первого рода: деградации на самом деле нет, но мы думаем, что есть. Так называемый false positive.
- Ошибка второго рода: деградация есть, но мы думаем, что её нет. Это false negative.
- Ошибка третьего рода: ситуация, когда мы получили ответ не на тот вопрос, на который мы хотели ответить. На мой взгляд, это самая главная ошибка, но её анализом зачастую пренебрегают.
Теперь поговорим о вероятностях этих ошибок.
Вероятность ошибки первого рода обозначается буквой α. Магическое значение по умолчанию, которое все зачем-то используют, составляет 0,05.
Вероятность ошибки второго рода обозначается буквой β. Тут у нас появляется ещё одна магическая константа в качестве значения по умолчанию она равна 0,20.
Вероятность ошибки третьего рода никак не обозначается и её никто не считает, но в среднем по больнице она очень большая.
Давайте теперь поговорим про характеристики статистических тестов и приведённые магические числа.
Самая главная характеристика называется уровень статистической значимости, который совпадает с α.
Одно из первых упоминаний 0,05 в качестве дефолтного значения можно найти в работе Фишера 1935 года. Там всё написано на иностранном языке, поэтому я решил засунуть этот текст в Google Translate и перевести на понятный язык — на C#.
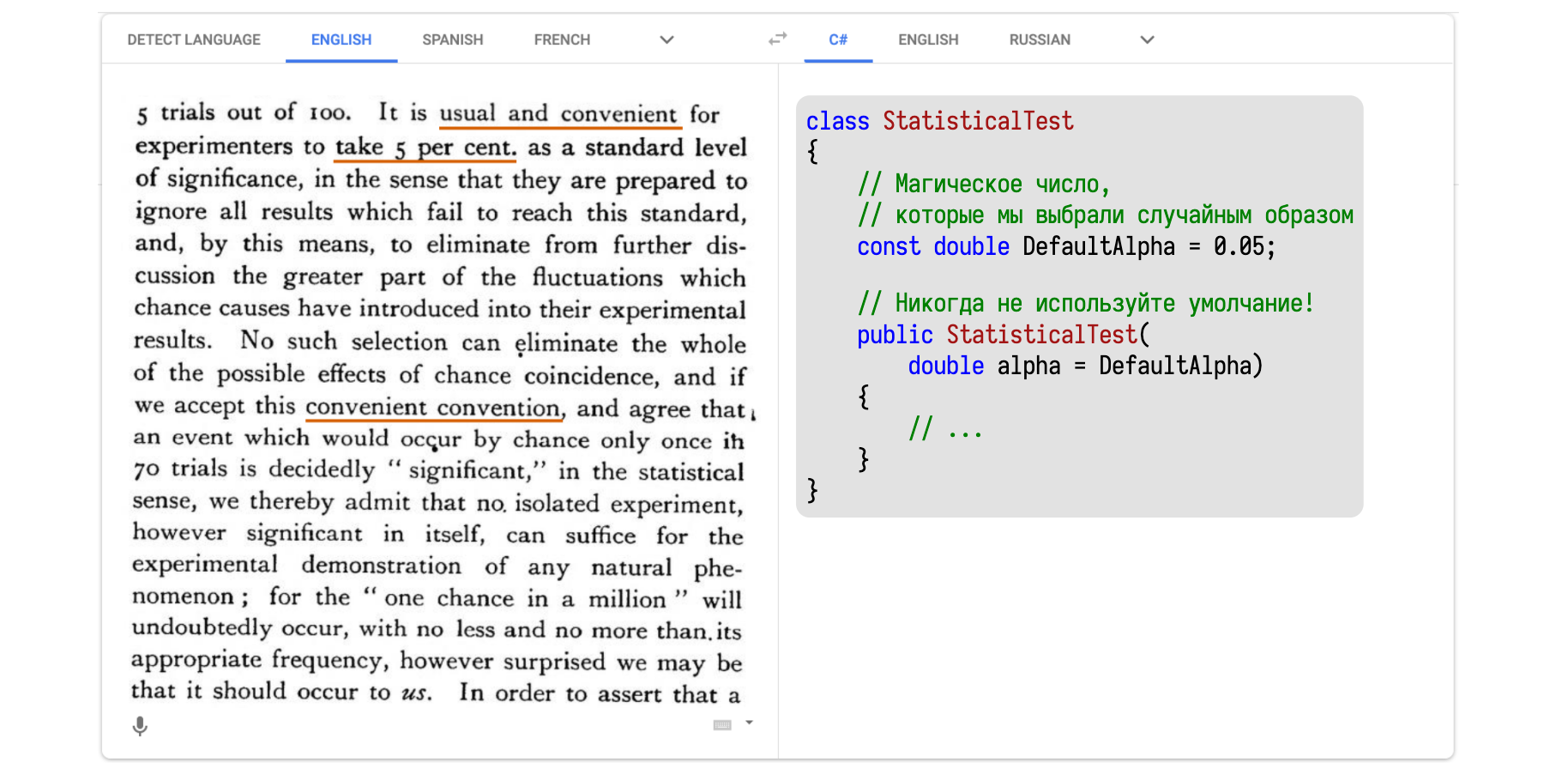
В тексте написано примерно следующее: мол, надо хорошенько подумать, что брать в качестве значения для α, но думать сложно и лень. Поэтому давайте придумаем удобное соглашение о значении по умолчанию, чтобы хоть что-то было, от чего можно отталкиваться. Мотивацию для выбора именно 0,05 можно найти в другой работе Фишера 1926 года в сельскохозяйственном журнале, где он пишет о том, как правильно оценивать эффективность удобрения полей навозом.
Перейдём ко второй характеристике статистических тестов, которая называется статистическая мощность. И равна она не β, как некоторые могли подумать, а 1 — β. Просто потому, что математики очень любят консистентность.
Волшебное число 0,20 можно найти в работе Коэна 1988 года. Тут тоже иностранный язык. Засовываем текст в Google Translate и получаем C#-версию.
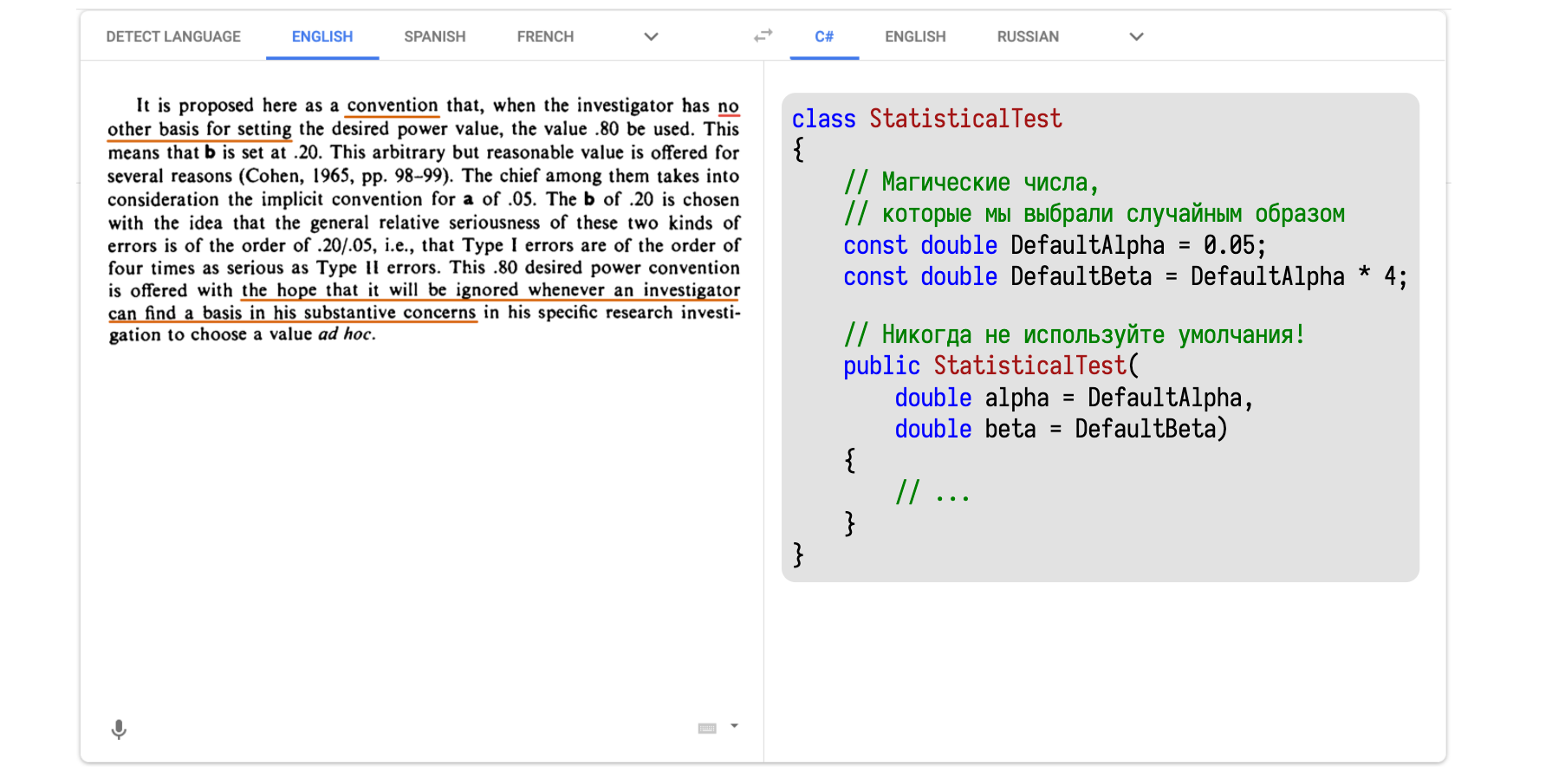
Тут написано, что нужно всегда тщательно думать о том, что взять в качестве β.
И только если у нас совсем нет никаких идей о том, что именно изучается, зачем изучается, то можно взять 0,2. А получилось это число благодаря умножению известных нам 0,05 на 4. Четвёрка тоже взята с потолка.
То есть Коэн умножил одно случайное магическое число на другое случайное магическое число, получил 0,2 и обрёк несколько поколений математиков на использование этого значения в качестве индустриального стандарта.
К счастью, заниматься анализом мощности довольно сложно, поэтому в подавляющем большинстве случаев столь важный этап проведения статистического теста благополучно игнорируется. Но вот с α приходится как-то работать, так как именно с ним сравнивается p-value.
Число очень неудобное и мешает работать, поэтому в случае слишком большого p-value математики придумывают эвфемизмы, чтобы обосновать значимость неудачных исследований: «почти значимый», «положительный тренд», «убедительный результат», «близкий к критическому уровню» и сотни других оправданий появляются в научных статьях каждый год. Особенно страшно становится, когда читаешь статьи по медицине, когда авторы пытаются как-то оправдать потраченные гранты. Но и в перформанс-анализе постоянно возникают проблемы. Просто система спроектирована так, что вызывает дикий соблазн сжульничать и использовать результаты статистического теста некорректным образом.
Использование статистических тестов
Давайте теперь попробуем использовать всё это на практике. Представим, что мы сделали 10000 итераций некоторого бенчмарка и стабильно получали значение около одной минуты.
Затем мы сделали некоторые изменения, выполнили одну итерацию и получили сразу 60 минут. Приходит менеджер и спрашивает, есть ли у нас тут перформанс-деградация.
Вменяемый инженер скажет, что скорее всего есть, но уверенности в этом нет.
Это мог быть единичный случай какого-то хитрого рейса, в результате которого всё зависло.
А статистический тест вообще ничего не скажет. Основная часть тестов считает дисперсию, которую нельзя подсчитать при наличии единственного замера.
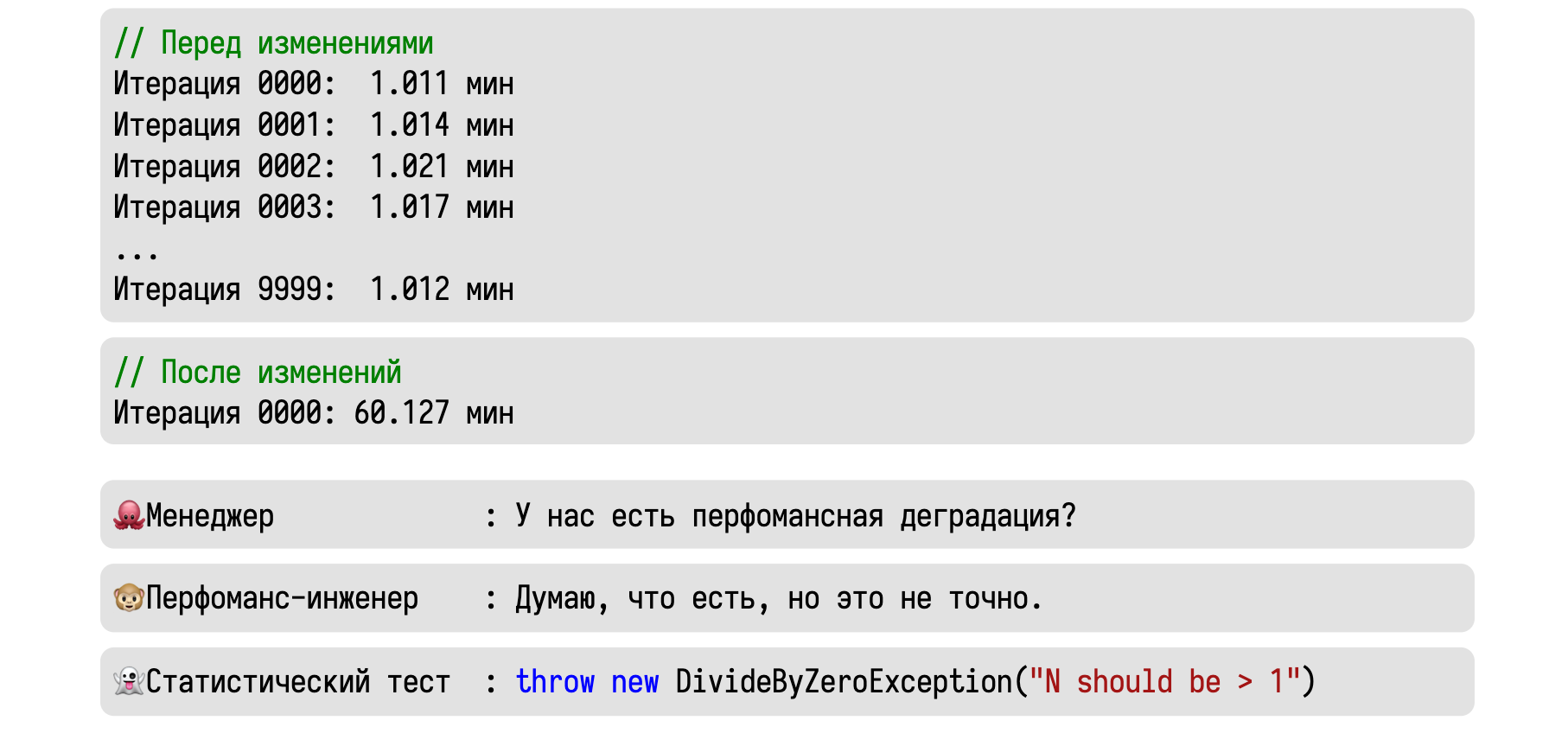
Давайте попробуем ещё раз. Начальные условия те же: 10000 итераций по одной минуте. После изменений в исходном коде мы выполнили три итерации, каждая из которых заняла час. Теперь, если менеджер спросит о том, есть ли у нас деградация, то хороший инженер ответит, что скорее всего есть.
Крайне маловероятно, что наш чудо-рейс не проявлял себя 10000 раз, а потом внезапно стрельнул три раза подряд. Стоит поизучать этот феномен и разобраться, куда же ушёл целый час. А статистический тест скажет нам, что нельзя отвергнуть нулевую гипотезу.
Многие думают, что этим он на самом деле хочет сказать, что деградации нет. Но в действительности он хочет сказать, что у нас недостаточно данных, чтобы обнаружить статистически значимую разницу. В статистике есть ещё одно магическое число: 30. Утверждается, что нам нужно сделать 30 итераций, чтобы чего-то значимое обнаружить. Но, согласитесь, глупо ждать 30 часов, чтобы убедиться в наличии проблемы. Да, в данной ситуации с тремя замерами мы не можем обнаружить статистически значимую разницу. Но мы можем обнаружить практически значимую разницу. А это намного важнее.
Ещё один пример: представьте, что вы добавили проверку на null в одном из методов.
Вы уверены, что null никогда не придёт, но на всякий случай решили это проверить.
Получаем стандартный вопрос от менеджера о том, есть ли у нас деградация. Нормальный инженер разумно рассудит, что мы добавили нового кода, а этот код занимает какое-то время. Значит, наш метод должен работать немного дольше.
А статистический тест опять нам скажет, что нельзя отвергнуть нулевую гипотезу.
На самом деле, в теории, если мы сделаем очень много итераций, то разницу можно будет и обнаружить. Но делать мы так, конечно, не будем.

В итоге получаем ситуацию, что вне зависимости от наличия или отсутствия маленькой деградации, статистический тест будет что-то бормотать про невозможность отвергания нулевой гипотезы. Бессмысленный результат, от которого довольно мало толка. А проблема в том, что мы совершили ошибку третьего рода: мы изначально задали неправильный вопрос.
Давайте попробуем ещё раз. Хороший менеджер должен был спросить, насколько велика деградация. Программисты каждый день пишут новый код и повсеместно вносят сотни деградаций в разные места. И это нормально. На практике мы не должны волноваться о всех деградациях, нас интересуют только самые большие деградации.
Хороший инженер скажет, что деградация очень маленькая, можно не волноваться.
Если бы мы сделали очень много итераций, то могли бы тут обнаружить статистически значимую разницу. Но вот только практически значимая разница бы всё равно не появилась. А вот статистические тесты на такой вопрос отвечать совсем не умеют, не эту задачу они решают.

В завершение этого раздела мне хотелось бы рассказать одну историю про использование p-value, за которую группа очень умных исследователей получила почётную награду по неврологии. Они занимались функциональной магнитно-резонансной томографией и решили провести следующий эксперимент. Подопытному показывали фотографии людей и спрашивали у него, какие по его мнению эмоции испытывают люди на фотографиях. Наборы фотографий показывались по 10 секунд, после чего подопытному давали 12 секунд на отдых. Общая продолжительность эксперимента составила почти 6 минут.
Полученные снимки фМРТ были проанализированы с помощью статистических тестов с пороговым значением для p-value 0,001, в результате чего были определены фотографии, которые вызывали определённые реакции в мозге. И это было бы абсолютно типичным исследованием, но вот только подопытным был… мёртвый атлантический лосось.
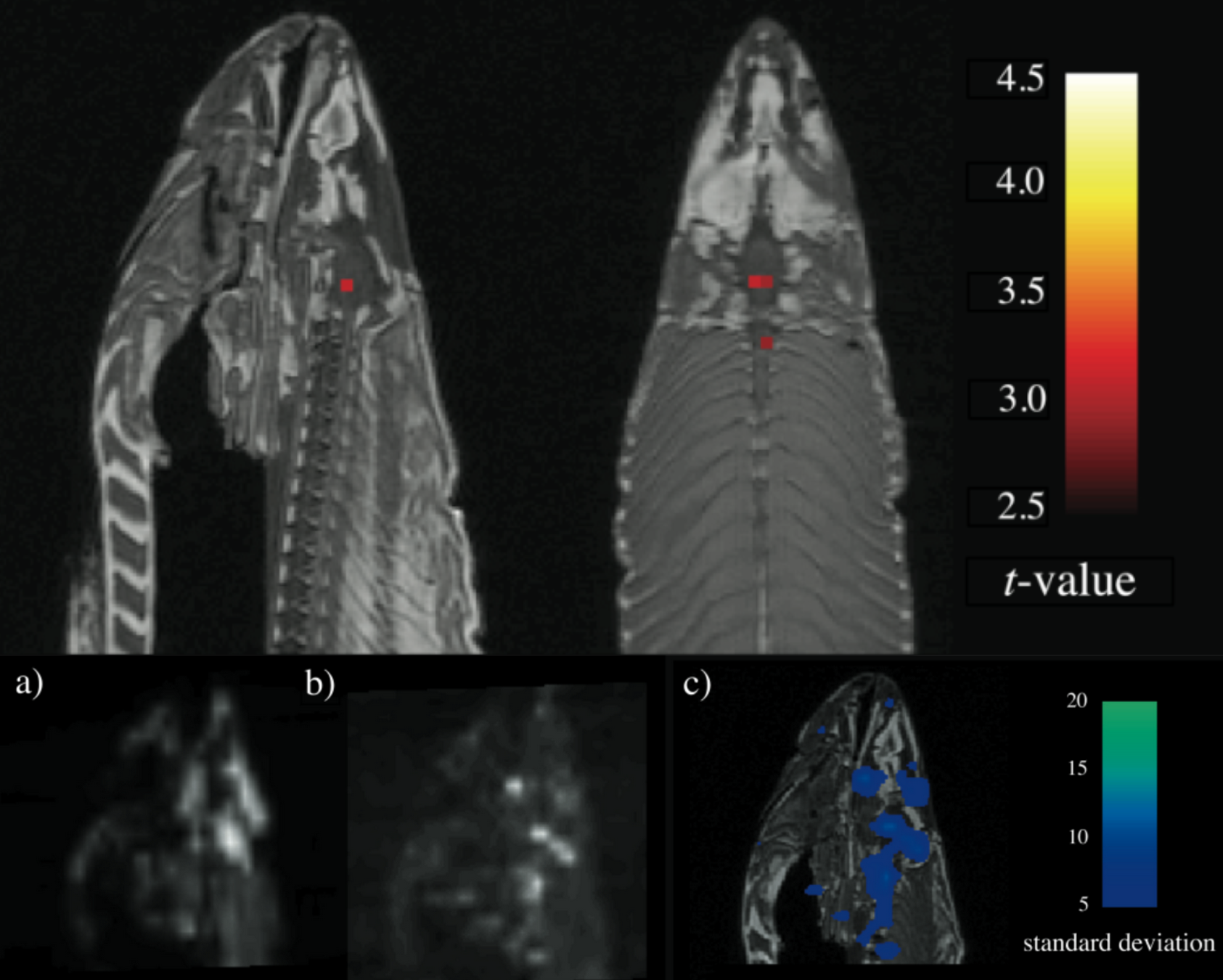
Всего за 6 минут учёные получили статистический значимый результат, который заключался в том, что у дохлой рыбы есть мозговая активность. А почётной наградой была Шнобелевская премия.
Резюмируем:
- Cтатистические тесты сложны для восприятия и использования.
- Они обладают множеством скрытых ограничений.
- У них всё очень плохо с воспроизводимостью.
- Они отвечают не на тот вопрос, на который мы хотим ответить.
Если вам неохота во всё это вникать, то можете просто запомнить, что статистические тесты просто не нужны в перформанс-анализе. Сразу хочу сказать, что это моё личное мнение, есть большое количество умных учёных, которые со мной не согласны.
Тут нужно понимать, что мы не говорим о том, что статистические тесты работают неправильно. Они хорошо решают ту задачу, для которой они создавались. Иногда они в каком-то виде могут решить вашу задачу и выдать более или менее вменяемые результаты. Но вот только в реальной жизни чаще всего можно использовать другие подходы, которые намного лучше справятся с вашими задачами.
Но довольно про
