Подсчёт с приблизительным распределением — чаще всего переизобретаемая сортировка

Количество более-менее отличающихся друг от друга сортировок гарантированно более сотни. Среди них есть подгруппы алгоритмов, минимально отличающиеся друг от друга, совпадая в какой-то общей главной идее. Фактически в разные годы разными людьми придумываются заново одни и те же сортировки, различающихся в не слишком принципиальных деталях.
Чаще прочих встречается вот такая алгоритмическая идея.
Каждый элемент заносится примерно в то место массива, где он должен находиться. Получается почти упорядоченный массив. К которому или применяется сортировка вставками (она самая эффективная для обработки почти упорядоченных массивов) или локальные неупорядоченные области обрабатываются рекурсивно этим же алгоритмом.
Статья написана при поддержке компании EDISON Software, разрабатывающая широкий спектр решений для разнообразных задач: от программ для онлайн-примерки одежды мультибрендовых магазинов до светодиодной системы передачи между речными и морскими судами.Мы очень любим теорию алгоритмов! ;-)
Чтобы оценить, примерно куда нужно поставить элемент, нужно выяснить, насколько он отличается от среднестатистического элемента массива. Для этого нужно знать значения минимального и максимального элементов, ну и размер массива.
Предполагается, что в сортируемом массиве действительно случайные данные. Все изобретатели данного метода приходят к одной и той же формуле:
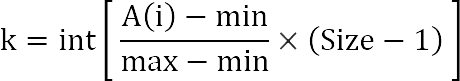
k — приблизительное место в массиве, где должен находиться элемент A(i)
min, max — значения минимального и максимального элементов в массиве A
Size — количество элементов в массиве A
Вот такая вот общая идея. Давайте поглядим, в каких вариациях этот алгоритм рождался снова и снова.
Сортировка царя Соломона :: Solomon sort

Этот способ (и его красивое название) предложил хабрапользователь V2008n лет 5 назад. Всему своё время, «время разбрасывать камни и время собирать камни» (слова царя Соломона из книги Екклесиаста) —, а в алгоритме, собственно так и происходит. Сначала с помощью формулы раскидываем элементы по нужным местам массива. Поскольку формула даёт не точное, а примерное место, то на некоторые позиции претендуют сразу несколько элементов, близких к друг другу по значению. Эти локальные группы элементов сортируются вставками и затем собираются в окончательном порядке.
Сортировка интерполяцией :: Interpolation sort
«Нет ничего нового под солнцем», если вновь процитировать того же автора. В Википедии описана сортировка интерполяцией, подозрительно напоминающая соломонову сортировку. Каждая «кучка камней» — это небольшой дополнительный динамический массив, где находятся близкие по значению элементы. Главное отличие — после «разбрасывания камней» эти локальные неотсортированные группы элементов сортируются не вставками, а самой же сортировкой интерполяцией (рекурсивно или в цикле).
Упорядоченный массив представляет из себя дискретный набор данных, который можно рассматривать как конечное множество известных значений некой неизвестной функции. Собственно, приблизительное распределение с точки зрения вычислительной математики — это интерполяция и есть.
Array.prototype.interpolationSort = function() {
var divideSize = new Array();
var end = this.length;
divideSize[0] = end;
while(divideSize.length > 0) {divide(this);}
function divide(A) {
var size = divideSize.pop();
var start = end - size;
var min = A[start];
var max = A[start];
var temp = 0;
for(var i = start + 1; i < end; i++) {
if(A[i] < min) {
min = A[i];
} else {
if(A[i] > max) {max = A[i];}
}
}
if(min == max) {
end = end - size;
} else {
var p = 0;
var bucket = new Array(size);
for(var i = 0; i < size; i++) {bucket[i] = new Array();}
for(var i = start; i < end; i++) {
p = Math.floor(((A[i] - min) / (max - min)) * (size - 1));
bucket[p].push(A[i]);
}
for(var i = 0; i < size; i++) {
if(bucket[i].length > 0) {
for(var j = 0; j < bucket[i].length; j++) {A[start++] = bucket[i][j];}
divideSize.push(bucket[i].length);
}
}
}
}
};Array.prototype.bucketSort = function() {
var start = 0;
var size = this.length;
var min = this[0];
var max = this[0];
for(var i = 1; i < size; i++) {
if (this[i] < min) {
min = this[i];
} else {
if(this[i] > max) {max = this[i];}
}
}
if(min != max) {
var bucket = new Array(size);
for(var i = 0; i < size; i++) {bucket[i] = new Array();}
var interpolation = 0;
for(var i = 0; i < size; i++){
interpolation = Math.floor(((this[i] - min) / (max - min)) * (size - 1));
bucket[interpolation].push(this[i]);
}
for(var i = 0; i < size; i++) {
if(bucket[i].length > 1) {bucket[i].bucketSort();} //Recursion
for(var j = 0; j < bucket[i].length; j++) {this[start++] = bucket[i][j];}
}
}
};Гистограмная сортировка :: Histogram sort
Это оптимизация сортировки интерполяцией, в которой подсчитывается количество элементов, принадлежащих к локальным неотсортированным группам. Этот подсчёт позволяет вставлять неотсортированные предметы непосредственно в итоговый массив (вместо группирования по отдельным небольшим массивам).
Array.prototype.histogramSort = function() {
var end = this.length;
var sortedArray = new Array(end);
var interpolation = new Array(end);
var hitCount = new Array(end);
var divideSize = new Array();
divideSize[0] = end;
while(divideSize.length > 0) {distribute(this);}
function distribute(A) {
var size = divideSize.pop();
var start = end - size;
var min = A[start];
var max = A[start];
for(var i = start + 1; i < end; i++) {
if (A[i] < min) {
min = A[i];
} else {
if (A[i] > max) {max = A[i];}
}
}
if (min == max) {
end = end - size;
} else {
for(var i = start; i < end; i++){hitCount[i] = 0;}
for(var i = start; i < end; i++) {
interpolation[i] = start + Math.floor(((A[i] - min) / (max - min)) * (size - 1));
hitCount[interpolation[i]]++;
}
for(var i = start; i < end; i++) {
if(hitCount[i] > 0){divideSize.push(hitCount[i]);}
}
hitCount[end - 1] = end - hitCount[end - 1];
for(var i = end - 1; i > start; i--) {
hitCount[i - 1] = hitCount[i] - hitCount[i - 1];
}
for(var i = start; i < end; i++) {
sortedArray[hitCount[interpolation[i]]] = A[i];
hitCount[interpolation[i]]++;
}
for(var i = start; i < end; i++) {A[i] = sortedArray[i];}
}
}
};Сортировка интерполяцией с метками
Чтобы ещё больше оптимизировать накладные расходы, тут предлагается запоминать не количество близких по значению элементов в неотсортированных группах, а просто помечать флажками True/False начало этих групп. True означает что подгруппа уже отсортирована, а False — что ещё нет.
Array.prototype.InterpolaionTagSort = function() {
var end = this.length;
if(end > 1) {
var start = 0 ;
var Tag = new Array(end); //Algorithm step-1
for(var i = 0; i < end; i++) {Tag[i] = false;}
Divide(this);
}
//Algorithm step-2
while(end > 1) {
while(Tag[--start] == false){} //Find the next bucket's start
Divide(this);
}
function Divide(A) {
var min = A[start];
var max = A[start];
for(var i = start + 1; i < end; i++) {
if(A[i] < min) {
min = A[i];
} else {
if(A[i] > max ) {max = A[i];}
}
}
if(min == max) {
end = start;
} else {
//Algorithm step-3 Start to be the next bucket's end
var interpolation = 0;
var size = end - start;
var Bucket = new Array(size);//Algorithm step-4
for(var i = 0; i < size; i++) {Bucket[i] = new Array();}
for(var i = start; i < end; i++) {
interpolation = Math.floor(((A[i] - min) / (max - min)) * (size - 1));
Bucket[interpolation].push(A[i]);
}
for(var i = 0; i < size; i++) {
if(Bucket[i].length > 0) {//Algorithm step-5
Tag[start] = true;
for(var j = 0; j < Bucket[i].length; j++) {A[start++] = Bucket[i][j];}
}
}
}
}//Algorithm step-6
};Сортировка интерполяцией с метками (на месте)
Если значения элементов в массиве не повторяются и равномерно распределены (грубо говоря — если данные в отсортированном виде представляют из себя что-то вроде арифметической прогрессии), то можно отсортировать в один проход, сортируя прямо на месте, не перемещая элементы в промежуточные массивы.
Array.prototype.InPlaceTagSort = function() {
var n = this.length;
var Tag = new Array(n);
for(i = 0; i < n; i++) {Tag[i] = false;}
var min = this[0];
var max = this[0];
for(i = 1; i < n; i++) {
if(this[i] < min) {
min = this[i];
} else {
if(this[i] > max) {max = this[i];}
}
}
var p = 0;
var temp = 0;
for(i = 0; i < n; i++) {
while(Tag[i] == false) {
p = Math.floor(((this[i] - min) / (max - min)) * (n - 1));
temp = this[i];
this[i] = this[p];
this[p] = temp;
Tag[p] = true;
}
}
};Флеш-сортировка :: Flashsort
Давным-давно я уже писал про сортировку, которую придумал профессор биофизики Нойберт в 1998 году.
Профессор предложил распределить элементы по нескольким отдельным классам (принадлежность к классу определяется размером элемента). С учётом этого формула выглядит так:
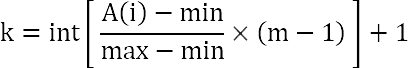
Вместо Size (размер массива) в формуле указано m — количество классов, по которым распределяем элементы массива. Формула вычисляет не ключ в массиве, куда надо перебросить элемент, а номер класса, к которому элемент относится.
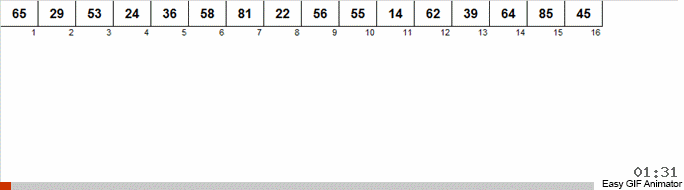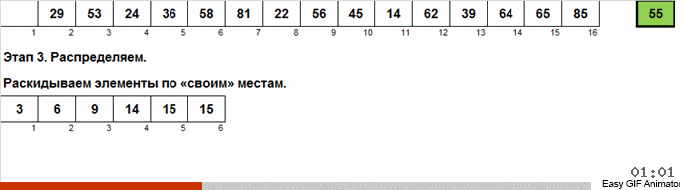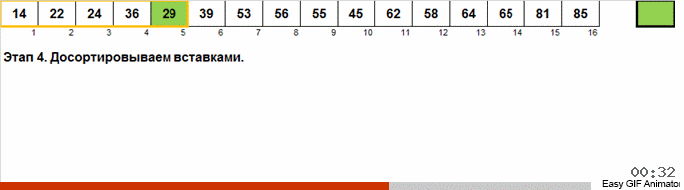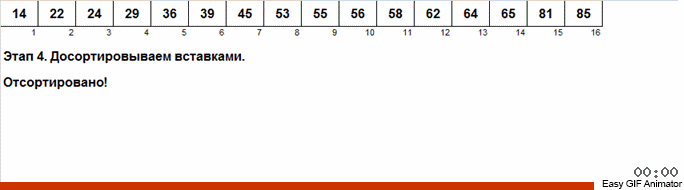
Эта сортировка неплоха тем, что более экономно относится к дополнительной памяти. Перераспределение элементов происходит на месте. Отдельно хранятся только локализации классов (ну, если посмотреть под другим ракурсом — отдельно хранятся количества элементов, принадлежащих к тому или иному классу).
Ну, а в остальном, — та же самая песня.
/**
* FlashSort.java - integer version
* Translation of Karl-Dietrich Neubert's algorithm into Java by
* Rosanne Zhang
*/
class FlashSort {
static int n;
static int m;
static int[] a;
static int[] l;
/* constructor
@param size of the array to be sorted */
public static void flashSort(int size) {
n = size;
generateRandomArray();
long start = System.currentTimeMillis();
partialFlashSort();
long mid = System.currentTimeMillis();
insertionSort();
long end = System.currentTimeMillis();
// print the time result
System.out.println("Partial flash sort time : " + (mid - start));
System.out.println("Straight insertion sort time: " + (end - mid));
}
/* Entry point */
public static void main(String[] args) {
int size = 0;
if (args.length == 0) {
usage();
System.exit(1);
}
try {
size = Integer.parseInt(args[0]);
}
catch (NumberFormatException nfe) {
usage();
System.exit(1);
}
FlashSort.flashSort(size);
}
/* Print usage */
private static void usage() {
System.out.println();
System.out.println("Usage: java FlashSort n ");
System.out.println(" n is size of array to sort");
}
/* Generate the random array */
private static void generateRandomArray() {
a = new int[n];
for(int i=0; i < n; i++) {
a[i] = (int)(Math.random() * 5 * n);
}
m = n / 20;
l = new int[m];
}
/* Partial flash sort */
private static void partialFlashSort() {
int i = 0, j = 0, k = 0;
int anmin = a[0];
int nmax = 0;
for(i=1; i < n; i++) {
if (a[i] < anmin) anmin=a[i];
if (a[i] > a[nmax]) nmax=i;
}
if(anmin == a[nmax]) return;
double c1 = ((double)m - 1) / (a[nmax] - anmin);
for(i=0; i < n; i++) {
k= (int) (c1 * (a[i] - anmin));
l[k]++;
}
for(k=1; k < m; k++) {
l[k] += l[k - 1];
}
int hold = a[nmax];
a[nmax] = a[0];
a[0] = hold;
int nmove = 0;
int flash;
j = 0;
k = m - 1;
while(nmove < n - 1) {
while(j > (l[k] - 1)) {
j++;
k = (int) (c1 * (a[j] - anmin));
}
flash = a[j];
while(!(j == l[k])) {
k = (int) (c1 * (flash - anmin));
hold = a[l[k] - 1];
a[l[k] - 1] = flash;
flash = hold;
l[k]--;
nmove++;
}
}
}
/* Straight insertion sort */
private static void insertionSort() {
int i, j, hold;
for(i = a.length - 3; i >= 0; i--) {
if(a[i + 1] < a[i]) {
hold = a[i];
j = i;
while (a[j + 1] < hold) {
a[j] = a[j + 1];
j++;
}
a[j] = hold;
}
}
}
/* For checking sorting result and the distribution */
private static void printArray(int[] ary) {
for(int i=0; i < ary.length; i++) {
if((i + 1) % 10 ==0) {
System.out.println(ary[i]);
} else {
System.out.print(ary[i] + " ");
}
System.out.println();
}
}
}Сортировка аппроксимацией :: Proxmap sort
Эта сортировка самая древняя из здесь упоминаемых, её в 1980 году представил профессор Томас Стендиш из Университета Калифорнии. С виду она вроде существенно отличается, однако если присмотреться, всё то же самое.
Алгоритм оперирует таким понятием как хит — некое число, близкое по значению к некоторым элементом массива.
Чтобы определить, относится ли элемент массива к хиту, к элементу применяется апроксимирующая функция.
У профессора Стендиша сортировались массивы, состоящие из вещественных чисел. Апроксимирующей функцией являлось округление вещественных чисел в меньшую сторону до целого числа.
То есть, к примеру, если в массиве есть элементы 2.8, 2, 2.1, 2.6 и т.п. то хитом именно для этих чисел будет двойка.

Общий порядок действий:
- Применяем аппроксимирующую функцию к каждому элементу, определяя, какому хиту соответствует очередной элемент.
- Таким образом для каждого хита можем подсчитать количество элементов, соответствующих данному хиту.
- Зная количества элементов для всех хитов, определяем локализации хитов (границы слева) в массиве.
- Зная локализации хитов, определяем локализацию каждого элемента.
- Определив локализацию элемента, пытаемся вставить его на своё место в массиве. Если место уже занято, то или сдвигаем соседей вправо (если элемент меньше их), чтобы освободить место для элемента. Или правее вставляем сам элемент (если он больше соседей).
В качестве аппроксимирующей функции можно назначить какую угодно, исходя из общего характера данных в массиве. В современных реализациях этой сортировки хиты обычно определяются не путём откусывания дробной части, а с помощью нашей любимой формулы.
Array.prototype.ProxmapSort = function() {
var start = 0;
var end = this.length;
var A2 = new Array(end);
var MapKey = new Array(end);
var hitCount = new Array(end);
for(var i = start; i < end; i++) {hitCount[i] = 0;}
var min = this[start];
var max = this[start];
for (var i = start+1; i < end; i++){
if (this[i] < min) {
min = this[i];
} else {
if(this[i] > max) {max = this[i];}
}
}
//Optimization 1.Save the MapKey[i].
for (var i = start; i < end; i++) {
MapKey[i] = Math.floor(((this[i] - min ) / (max - min)) * (end - 1));
hitCount[MapKey[i]]++;
}
//Optimization 2.ProxMaps store in the hitCount.
hitCount[end-1] = end - hitCount[end - 1];
for(var i = end-1; i > start; i--){
hitCount[i-1] = hitCount[i] - hitCount[i - 1];
}
//insert A[i]=this[i] to A2 correct position
var insertIndex = 0;
var insertStart = 0;
for(var i = start; i < end; i++){
insertIndex = hitCount[MapKey[i]];
insertStart = insertIndex;
while(A2[insertIndex] != null) {insertIndex++;}
while(insertIndex > insertStart && this[i] < A2[insertIndex - 1]) {
A2[insertIndex] = A2[insertIndex - 1];
insertIndex--;
}
A2[insertIndex] = this[i];
}
for(var i = start; i < end; i++) {this[i] = A2[i];}
};Сортировка вставкой в хеш-таблицу :: Hash sort
Ну и закончим наш обзор алгоритмом, который предложил хабраюзер bobbyKdas 6 лет тому. Это гибридный алгоритм, в который помимо распределения и вставок добавлено также слияние.
- Массив рекурсивно делится пополам, пока на каком-то шаге размеры половинок-подмассивов не достигнут минимального размера (у автора это не более 500 элементов).
- На самом нижнем уровне рекурсии к каждой половинке-подмассиву применяется знакомый алгоритм — с помощью всё той же формулы внутри подмассива происходит приблизительное распределение, с сортировкой вставками локальных неотсортированных участков.
- После упорядочивания двух половинок-подмассивов происходит их слияние.
- Пункт 3 (слияние отсортированных половинок-подмассивов) повторяется при подъёме по уровням рекурсии до самого верха, когда из двух половинок объединяется исходный массив.
import java.util.Arrays;
import java.util.Date;
import java.util.Random;
public class HashSort {
//Размер массива исходных данных
static int SOURCELEN = 1000000;
int source[] = new int[SOURCELEN];
//Копия исходных данных для сравнения с быстрой сортировкой
int quick[] = new int[SOURCELEN];
//Размер блока для хэширующей сортировки
static int SORTBLOCK = 500;
static int k = 3;
//Временный массив
static int TMPLEN = (SOURCELEN < SORTBLOCK * k) ? SORTBLOCK * k : SOURCELEN;
int tmp[] = new int[TMPLEN];
//Диапазон значений исходных данных
static int MIN_VAL = 10;
static int MAX_VAL = 1000000;
int minValue = 0;
int maxValue = 0;
double hashKoef = 0;
//Заполнение массива исходных данных случайными значениями
public void randomize() {
int i;
Random rnd = new Random();
for(i=0; i maxValue) {
maxValue = source[i];
}
if( source[i] < minValue) {
minValue = source[i];
}
}
hashKoef = ((double)(k-1)*0.9)*((double)(endIndex-startIndex)/((double)maxValue-(double)minValue));
}
//Склеивание (иначе говоря - слияние) двух смежных отсортированных частей массива
public void stickParts(int startIndex, int mediana, int endIndex) {
int i=startIndex;
int j=mediana+1;
int k=0;
//Пока есть элементы в обоих подмассивах - производим их слияние
while(i<=mediana && j<=endIndex) {
if(source[i]mediana ) {
while(j<=endIndex) {
tmp[k] = source[j];
j++;
k++;
}
}
//Если в правом остались элементы - переносим в конец общего подмассива
if(j>endIndex) {
while(i<=mediana) {
tmp[k] = source[i];
i++;
k++;
}
}
System.arraycopy(tmp, 0, source, startIndex, endIndex-startIndex+1);
}
//Сдвиг вправо во временном массиве для разрешения коллизий
//Передвигаем несколько подряд стоящих элементов чтобы слева осовободить ячейку
boolean shiftRight(int index) {
int endpos = index;
while( tmp[endpos] != 0) {
endpos++;
if(endpos == TMPLEN) return false;
}
while(endpos != index ) {
tmp[endpos] = tmp[endpos-1];
endpos--;
}
tmp[endpos] = 0;
return true;
}
//Хэш-функция для сортировки хэшированием
public int hash(int value) {
return (int)(((double)value - (double)minValue)*hashKoef);
}
//Вставка значений во временный массив с разрешением коллизий
public void insertValue(int index, int value) {
int _index = index;
//Если место занято, то ищем правее
//двигаемся пока заняты ячейки и вставляемый элемент больше тех что уже в хеш-массиве
while(tmp[_index] != 0 && tmp[_index] <= value) { _index++; }
//Если всё ещё занято и дошли до элемента, который больше вставляемого
if( tmp[_index] != 0) {
shiftRight(_index);//Сдвигаем подряд идущие бОльшие элементы вправо
}
tmp[_index] = value;//Место свободно - вставляем элемент
}
//Копирование отсортированных данных из временного массива в исходный
public void extract(int startIndex, int endIndex) {
int j=startIndex;
for(int i=0; i<(SORTBLOCK*k); i++) {
if(tmp[i] != 0) {
source[j] = tmp[i];
j++;
}
}
}
//Очистка временного массива
public void clearTMP() {
if( tmp.length < SORTBLOCK*k) {
Arrays.fill(tmp, 0);
} else {
Arrays.fill(tmp, 0, SORTBLOCK*k, 0);
}
}
//Хэширующая сортировка
public void hashingSort(int startIndex, int endIndex) {
//1. Поиск минимального и максимального значения с вычислением хэширующего коэффициента
findMinMax(startIndex, endIndex);
//2. Очистка временного массива
clearTMP();
//3. Вставка во временный массив с использованием хэш-функции
for(int i=startIndex; i<=endIndex; i++) {
insertValue(hash(source[i]), source[i]);
}
//4. Перемещение отсортированных данных из временного массива в исходный
extract(startIndex, endIndex);
}
//Рекурсивный спуск с дихотомией до уровня блока хэширующей сортировки
public void sortPart(int startIndex, int endIndex) {
//Если размер подмассива меньше 500, то непосредственно хэш-сортируем
if((endIndex - startIndex) <= SORTBLOCK ) {
hashingSort(startIndex, endIndex);
return;
}
//Если размер > 500 то делим пополам и рекурсия к каждой половинке
int mediana = startIndex + (endIndex - startIndex) / 2;
sortPart(startIndex, mediana);//Рекурсия к левой половинке
sortPart(mediana+1, endIndex);//Рекурсия к правой половинке
stickParts(startIndex, mediana, endIndex);//Половинки рекурсивно отсортированы - склеиваем их
}
//Сортируем весь массив как максимально возможный подмассив
public void sort() {
sortPart(0, SOURCELEN-1);
}
public static void main(String[] args) {
HashSort hs = new HashSort();
hs.randomize();
hs.sort();
}
}
Сама формула здесь называется хеш-функцией, а вспомогательный массив для приблизительного распределения — хеш-таблицей.
Ссылки
 Interpolation & Histogram, Flash, Proxmap
Interpolation & Histogram, Flash, Proxmap
 Соломон, Хеш-таблица, Флеш
Соломон, Хеш-таблица, Флеш
Статьи серии:
В Excel-приложение AlgoLab появилась сортировка аппроксимацией (при этом в начальном неотсортированном массиве к целым числам дописывается рандомная дробная часть). Соломон и Флеш там уже давно, а вот интерполяцию, хеш и гистограмму пока не реализовал.

