Почему умножение матриц такое30.11.2022 22:32

Наверное, каждый задавался вопросом, почему умножение матриц такое. В этой статье мы разберём из каких соображений оно вводится именно так.

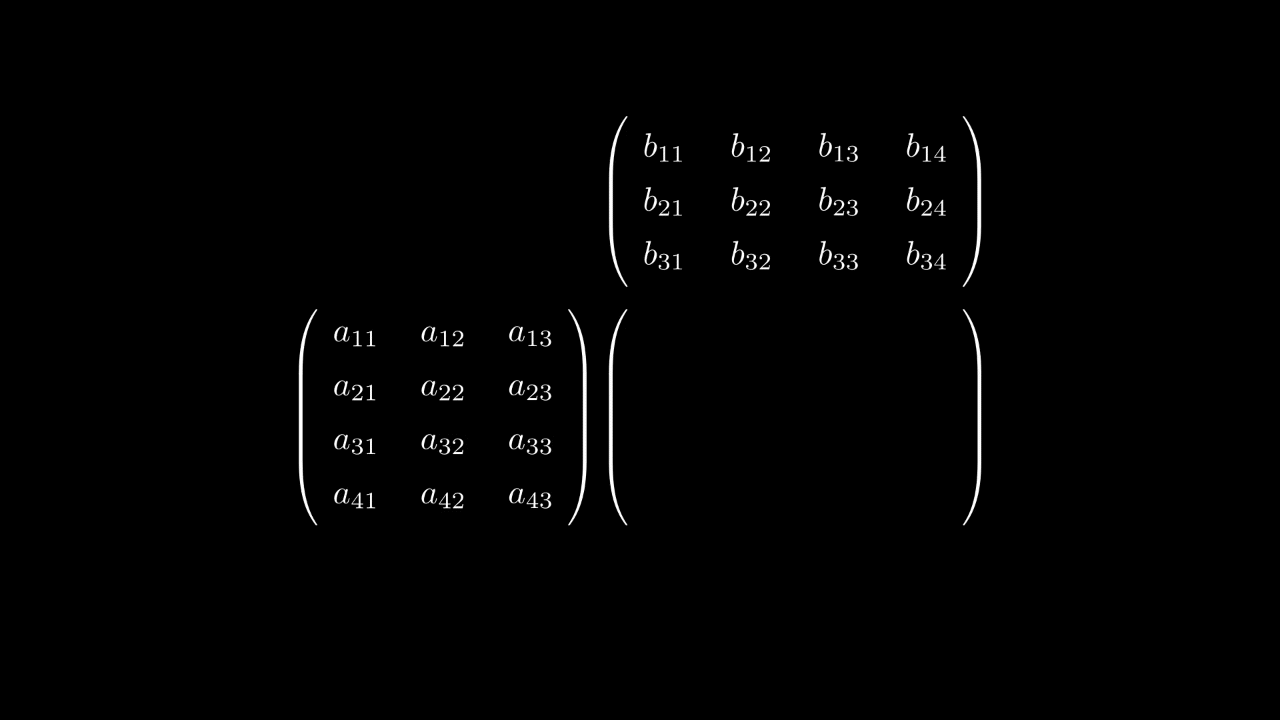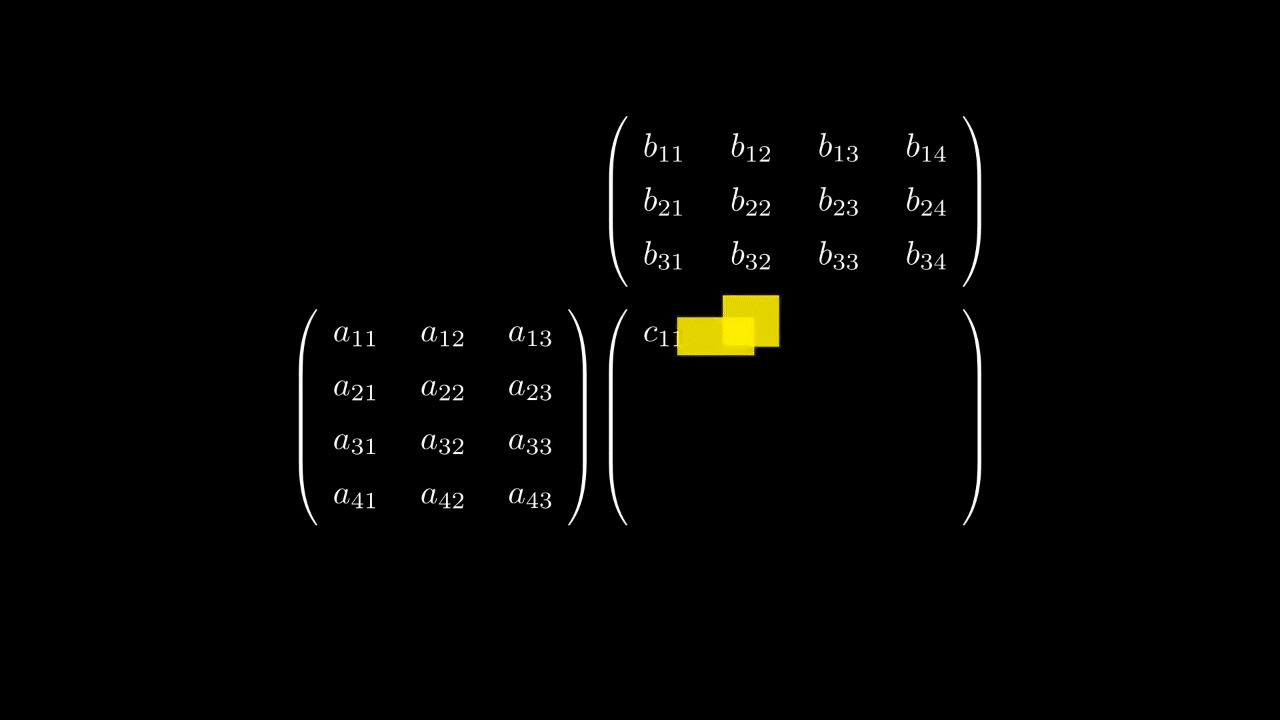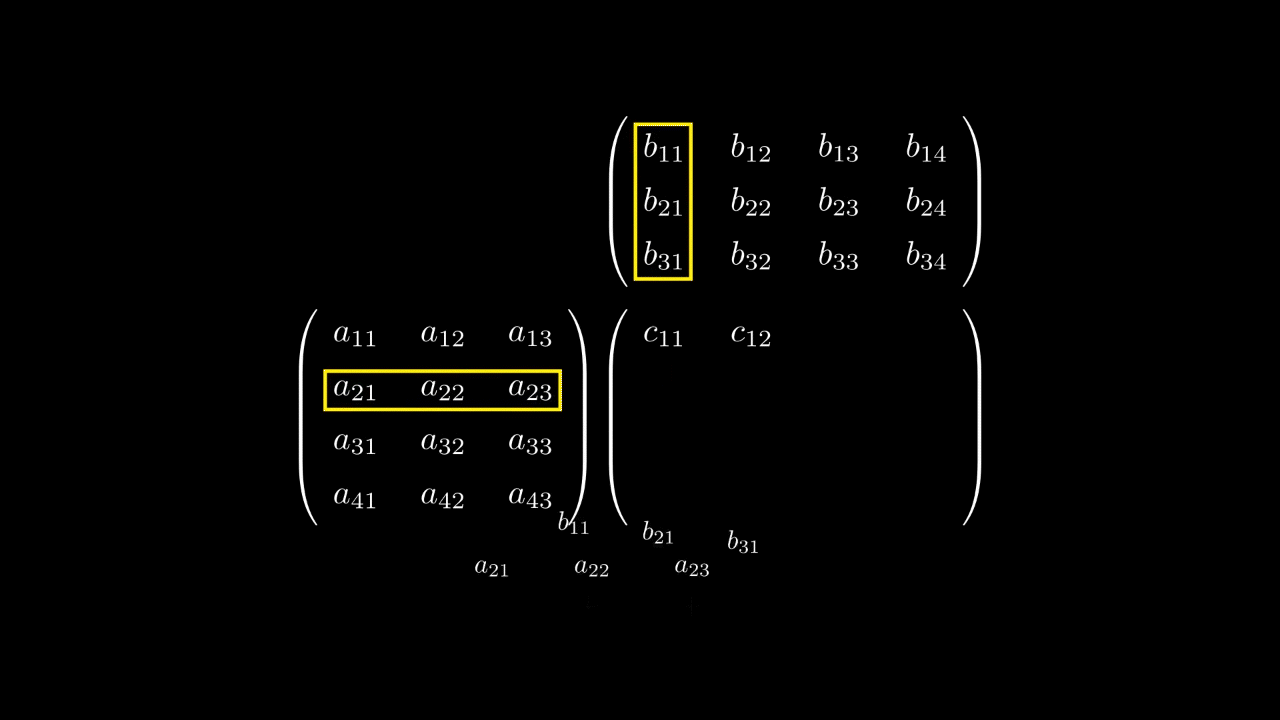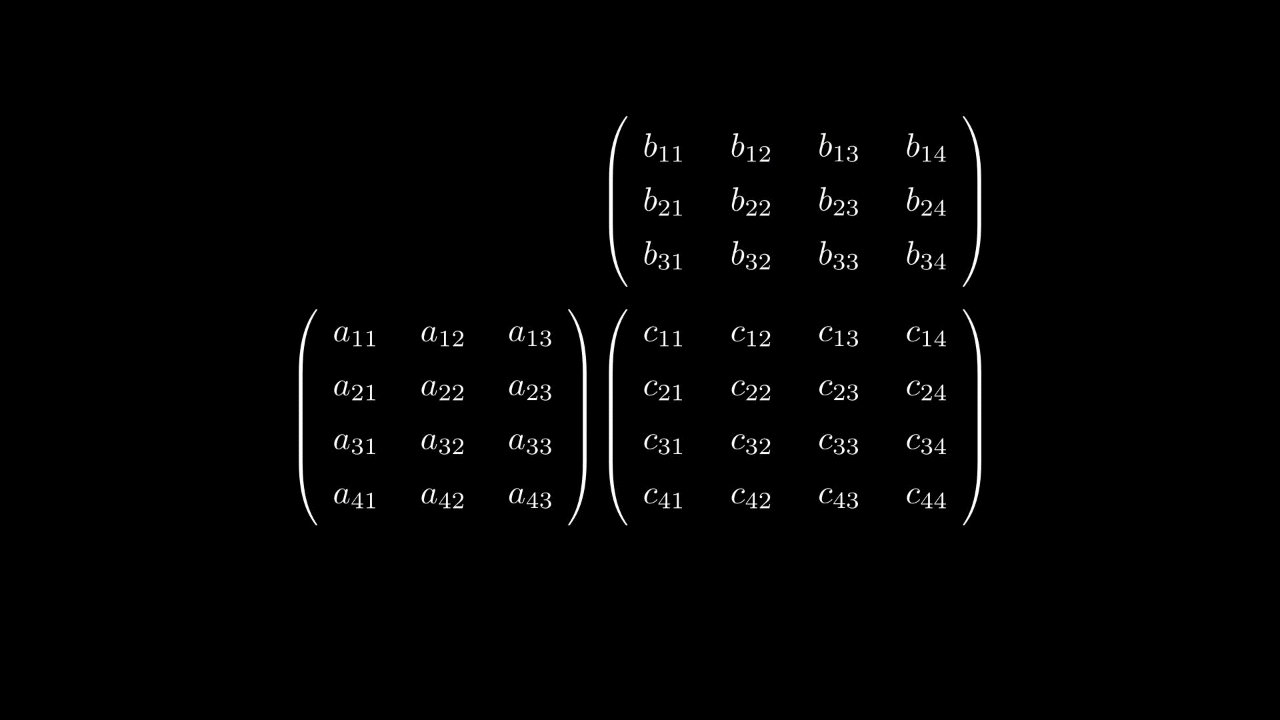
3122894fe15441ef8e81f74b1e8ffeb4.gif

Маленькое предисловие

В дальнейшем нам понадобится такая структура, как векторное пространство, а точнее его частный случай \mathbb{R}^n— пространство столбцов высотыnнад\mathbb{R}.Кратко напомню, чтопод этим понимается.

Во-первых, \mathbb{R}^n— это следующее множество

\mathbb{R}^n=\{[x_1,\ldots,x_n] \,|\,x_i\in\mathbb{R}\},

где таким образом [x_1,\ldots,x_n] обозначен вектор-столбец высотыn,то есть

[x_1,\ldots,x_n]=\left(\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right).

Во-вторых, для любых векторовx,y \in \mathbb{R}^nопределено сложение

x+y = [x_1,\ldots,x_n]+[y_1,\ldots,y_n]=[x_1+y_1,\ldots,x_n+y_n]

и для любого вектораx \in \mathbb{R}^nопределено умножение на скаляр\lambda \in \mathbb{R}

\lambda x = \lambda[x_1,\ldots,x_n] = [\lambda x_1,\ldots,\lambda x_n].

В-третьих, каждый векторx \in \mathbb{R}^nединственным образом представим в следующем виде

x=x_1e_1+\ldots+x_ne_n,

где x_1,\ldots,x_n— скаляры, а (e_1,\ldots,e_n) — следующая система векторов

e_1=[1,0,\ldots,0],\,e_2=[0,1,\ldots,0],\ldots,\,e_n=[0,0,\ldots,1].

Такая система векторов называется базис, а скаляры, участвующие в разложение вектора, называются координатами этого вектора в данном базисе. Стоит отметить, что в \mathbb{R}^nэто не единственный базис, но везде далее под «зафиксируем базис» можно понимать именно эту систему векторов.

Умножение матрицы на вектор

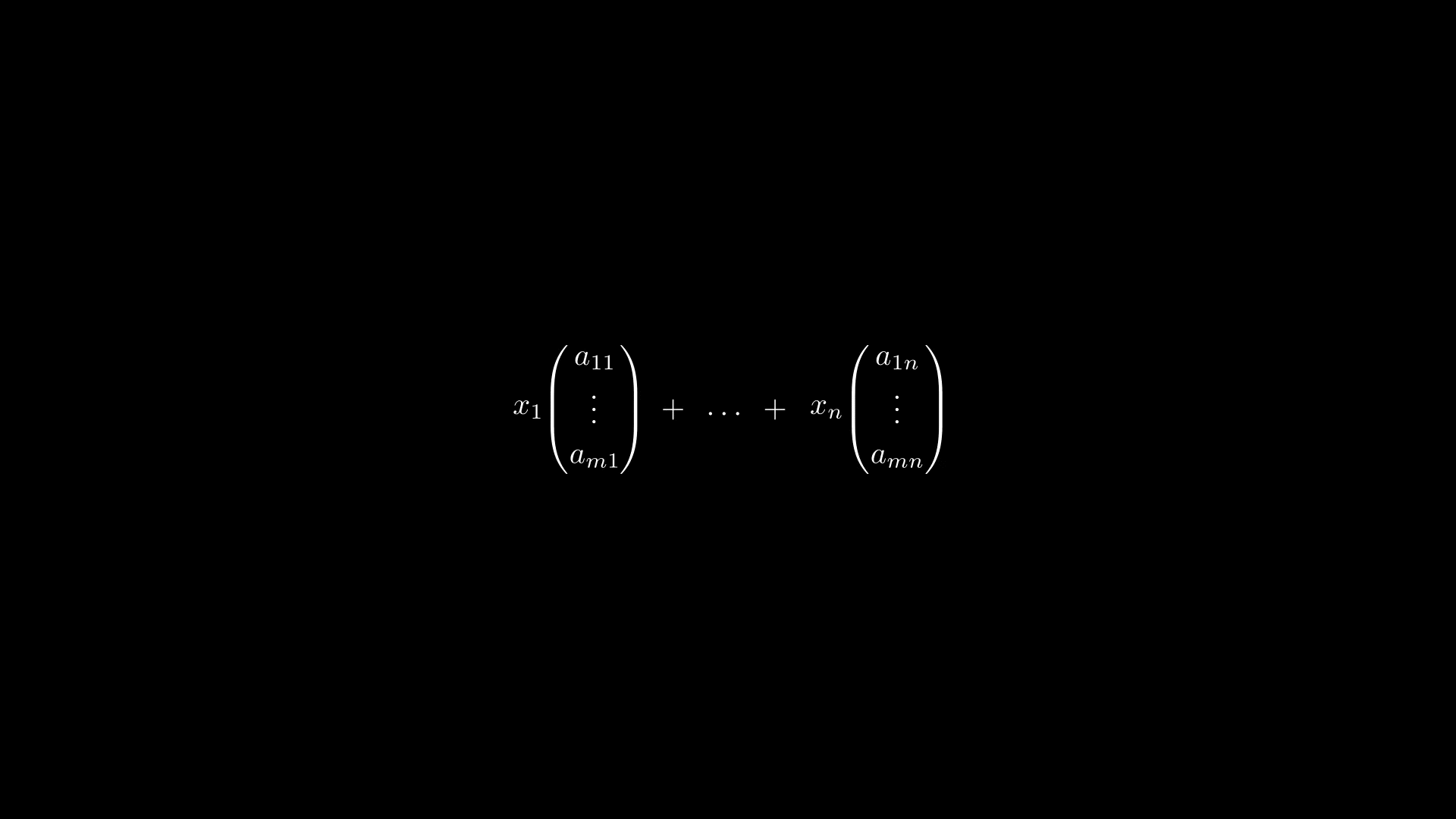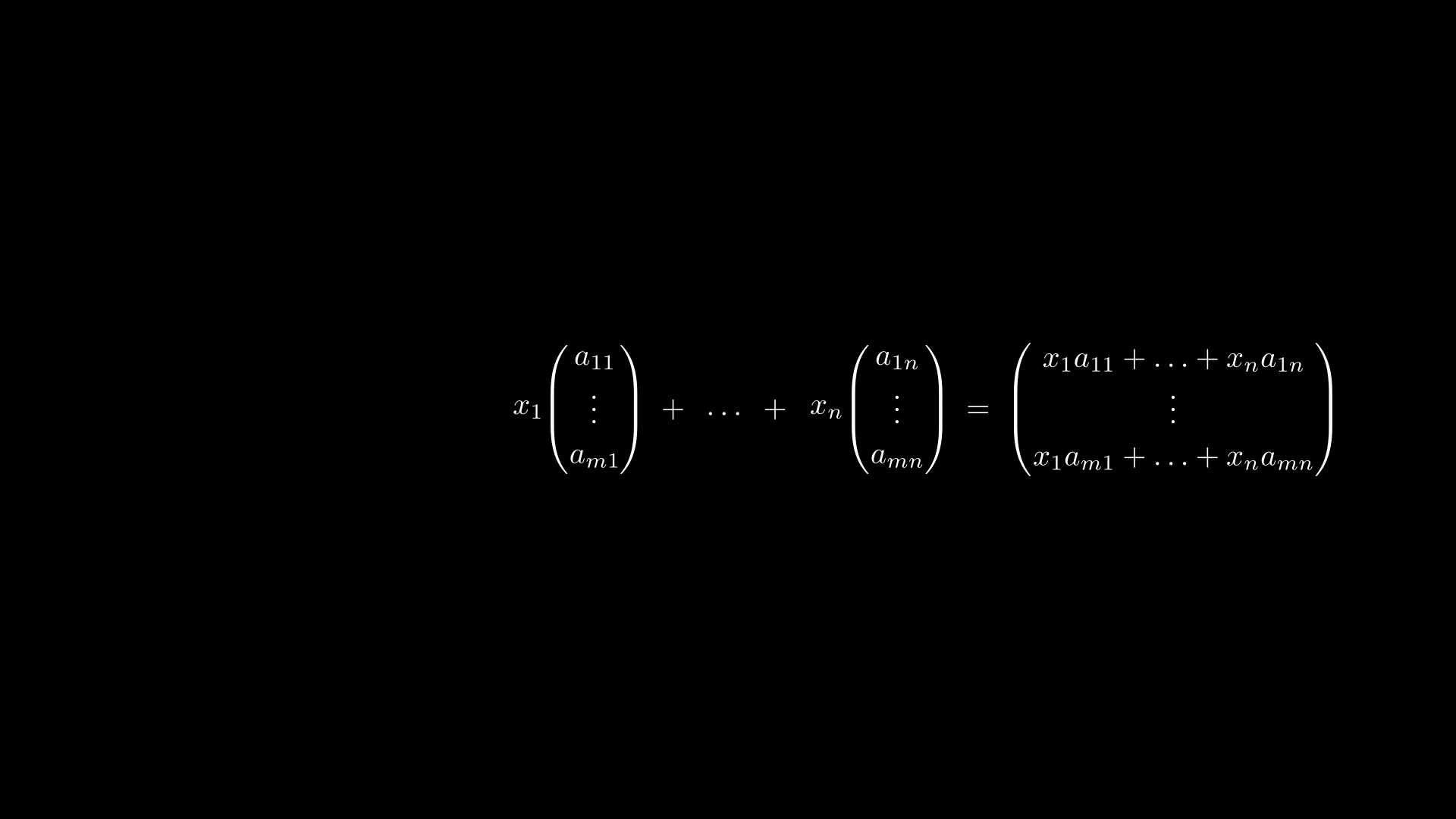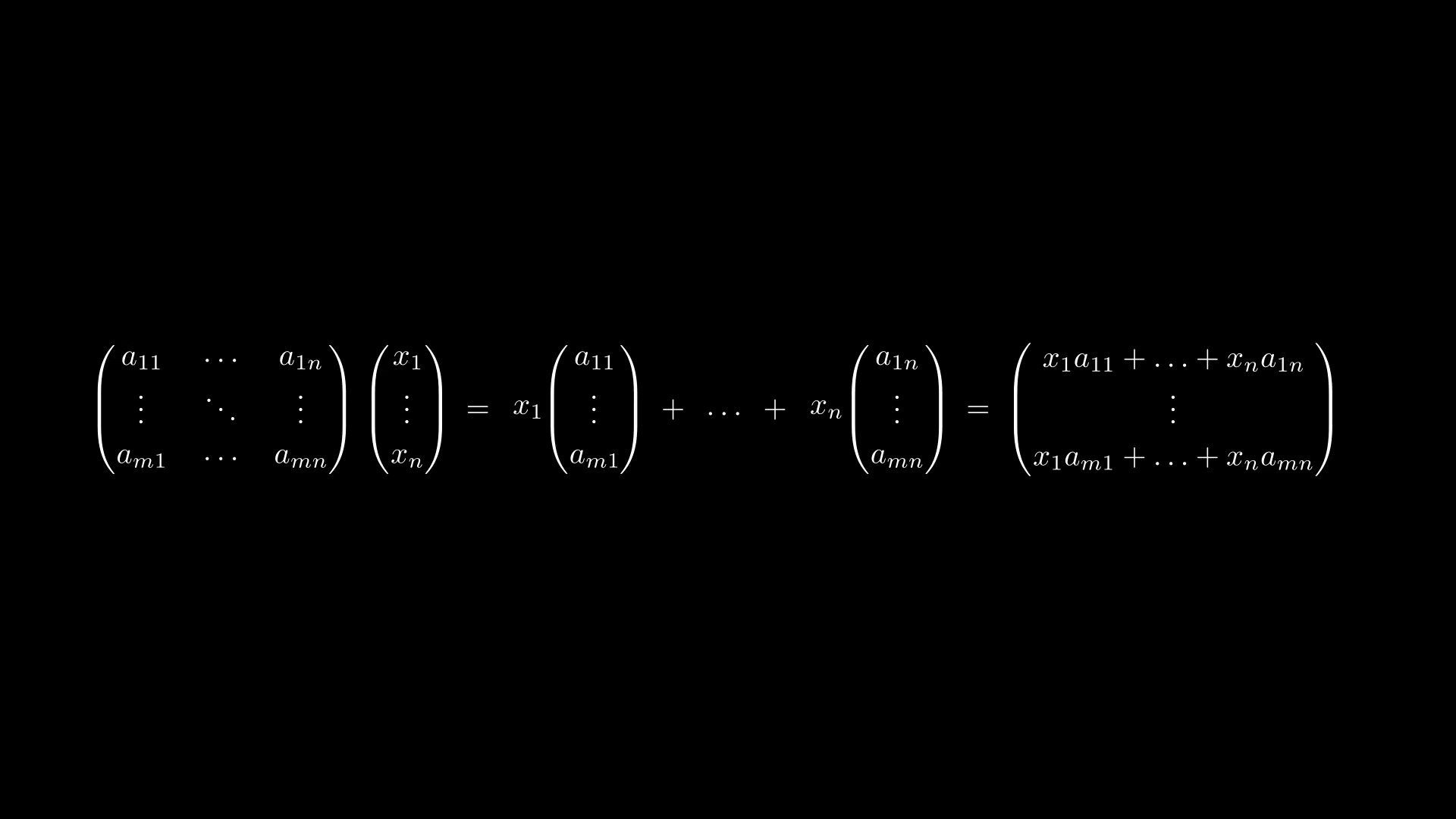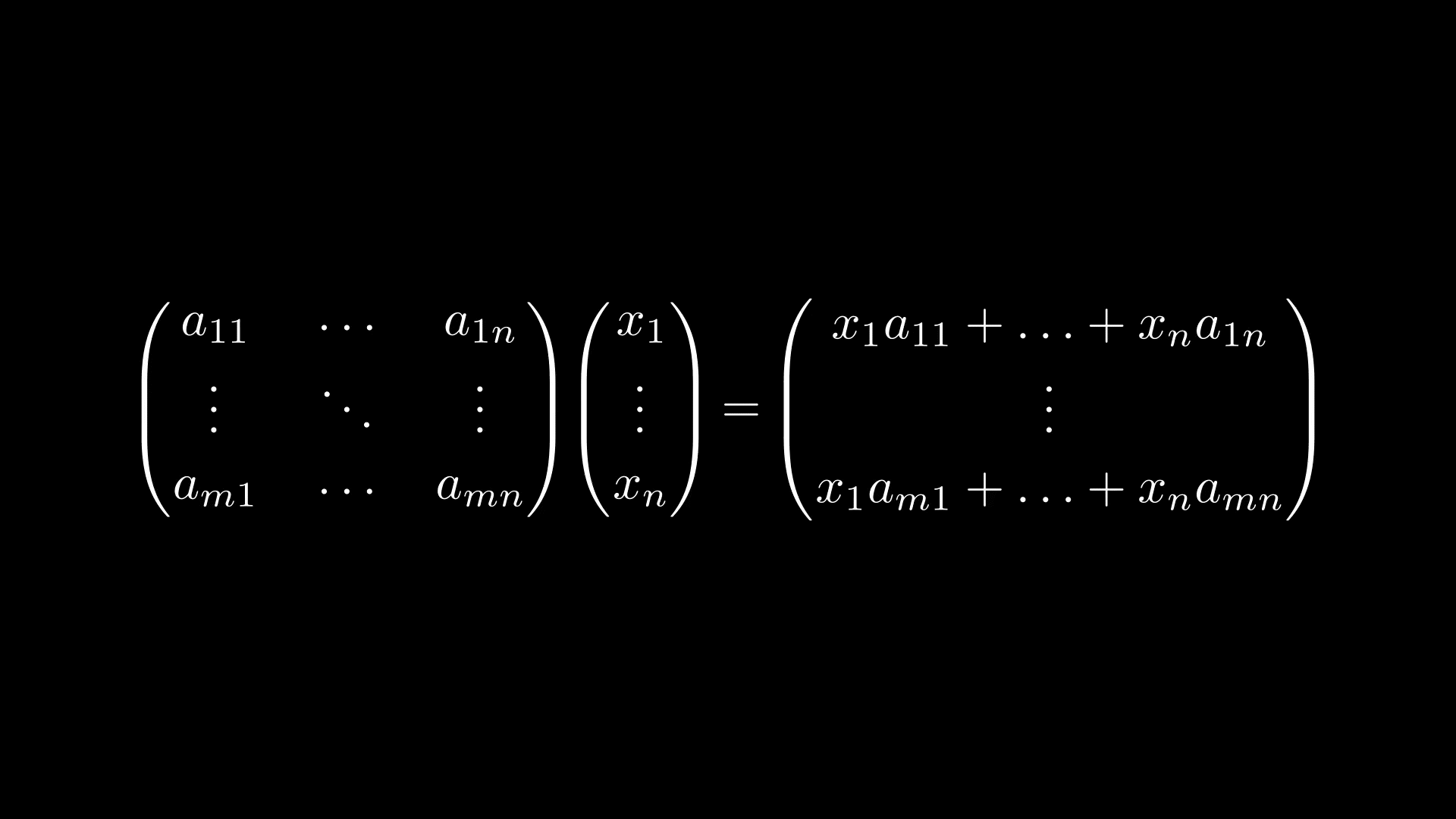
9374703e892b5d399a55122042f0163f.gif

Прежде чем переходить к умножению матриц, посмотрим, из каких соображений вводится умножение матрицы на вектор. Для этого рассмотрим линейное отображение\mathcal{A}

\mathcal{A}:\mathbb{R}^n \rightarrow \mathbb{R}^m.

То, что\mathcal{A}— линейное отображение, означает, что для любых векторовx,y \in \mathbb{R}^nи любого скаляра\lambda \in \mathbb{R}выполняются следующие два условия:

\begin{array}{l} \mathcal{A}(x+y)=\mathcal{A}x + \mathcal{A}y.\\ \mathcal{A}(\lambda x)=\lambda\mathcal{A}x. \end{array}

Или их можно объединить в одно

\mathcal{A}(\lambda_1 x + \lambda_2 y)=\lambda_1\mathcal{A} x + \lambda_2 \mathcal{A}y.

Нас интересует, как линейное отображение\mathcal{A}действует на произвольный векторx \in \mathbb{R}^n. Для этого зафиксируем в \mathbb{R}^nбазис (e_1,\ldots,e_n),а в \mathbb{R}^mбазис (f_1,\ldots,f_m).Теперь мы можем разложить векторxпо базису

x = x_1e_1+\ldots+x_ne_n

и представить\mathcal{A}xв следующем виде

\mathcal{A}x=\mathcal{A}(x_1e_1+\ldots+x_ne_n)=x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n.

Заметим, что \mathcal{A}e_1,\ldots,\mathcal{A}e_n \in \mathbb{R}^m,а поскольку в \mathbb{R}^mзафиксирован базис, то эти векторы также можно разложить по базису

\mathcal{A}e_1 = a_{11}f_1+a_{21}f_2+\ldots+a_{m1}f_m, \\ \mathcal{A}e_2 = a_{12}f_1+a_{22}f_2+\ldots+a_{m2}f_m, \\ \ldots \\ \mathcal{A}e_n = a_{1n}f_1+a_{2n}f_2+\ldots+a_{mn}f_m.

или тоже самое в векторной записи

\begin{array}{cccc} \mathcal{A}e_1 = \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right), & \mathcal{A}e_2 = \left( \begin{array}{c} a_{12}\\ \vdots \\ a_{m2} \end{array} \right), & \ldots &, & \mathcal{A}e_n = \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) \end{array}.

Подставляем в равенство выше и получаем

x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n= x_1 \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right) + \ldots + x_n \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) = \left( \begin{array}{c} x_1a_{11} + \ldots + x_na_{1n}\\ \vdots \\ x_1a_{m1} + \ldots + x_na_{mn} \end{array} \right)

Но правая часть равенства есть не что иное, как формула умножения матрицы на вектор-столбец

\left( \begin{array}{ccc} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array} \right) \left( \begin{array}{c} x_{1} \\ \vdots \\ x_n \end{array} \right),

где столбцы матрицы есть векторы \mathcal{A}e_1,\ldots,\mathcal{A}e_n

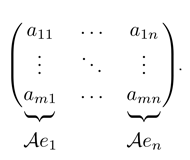
54e0656bd036eef1301be110570dd11a.png

Получается, можно ввести умножение матрицы на вектор по следующему правилу

\small \left( \begin{array}{ccc} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array} \right) \left( \begin{array}{c} x_{1} \\ \vdots \\ x_n \end{array} \right) = x_1 \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right) + \ldots + x_n \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) = \left( \begin{array}{c} x_1a_{11} + \ldots + x_na_{1n}\\ \vdots \\ x_1a_{m1} + \ldots + x_na_{mn} \end{array} \right).

И такое определение умножения будет согласовано с тем, как линейное отображение\mathcal{A}действует на векторx.

Если теперь обозначить y= \mathcal{A}x,то координаты вектора y выражаются через координаты вектора xследующим образом

y_i = \sum_{i=1}^{n}a_{ij}x_j,\quad i = 1,\ldots,m,

Кроме того, мы получили и другой важный результат, вернёмся к выражению для\mathcal{A}x

\mathcal{A}x=\mathcal{A}(x_1e_1+\ldots+x_ne_n)=x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n.

Из него следует, что линейное отображение\mathcal{A}полностью определяется своими значениями на базисных векторах, то есть, если нужно найти\mathcal{A}x,то достаточно знать\mathcal{A}e_1,\ldots,\mathcal{A}e_n.

Далее, мы поместили эти векторы в матрицу и определили умножение так, что\mathcal{A}xесть произведение соответствующей матрицыAнаx.Получается, что линейному отображению можно поставить в соответствие матрицу, которая полностью его определяет

\forall x \in \mathbb{R}^n: \mathcal{A}x = Ax.

Такая матрица называется матрицей линейного отображения\mathcal{A}в выбранных базисах пространств \mathbb{R}^nи \mathbb{R}^m.

Если говорить более строго, то существует взаимно однозначное соответствие между линейными отображениями из \mathbb{R}^nв \mathbb{R}^mи матрицами размера m \times n.

Теперь мы можем перейти к умножению матрицы на матрицу.

Умножение матрицы на матрицу

ed7b9f061229afced8347fab7cc3ea29.gif

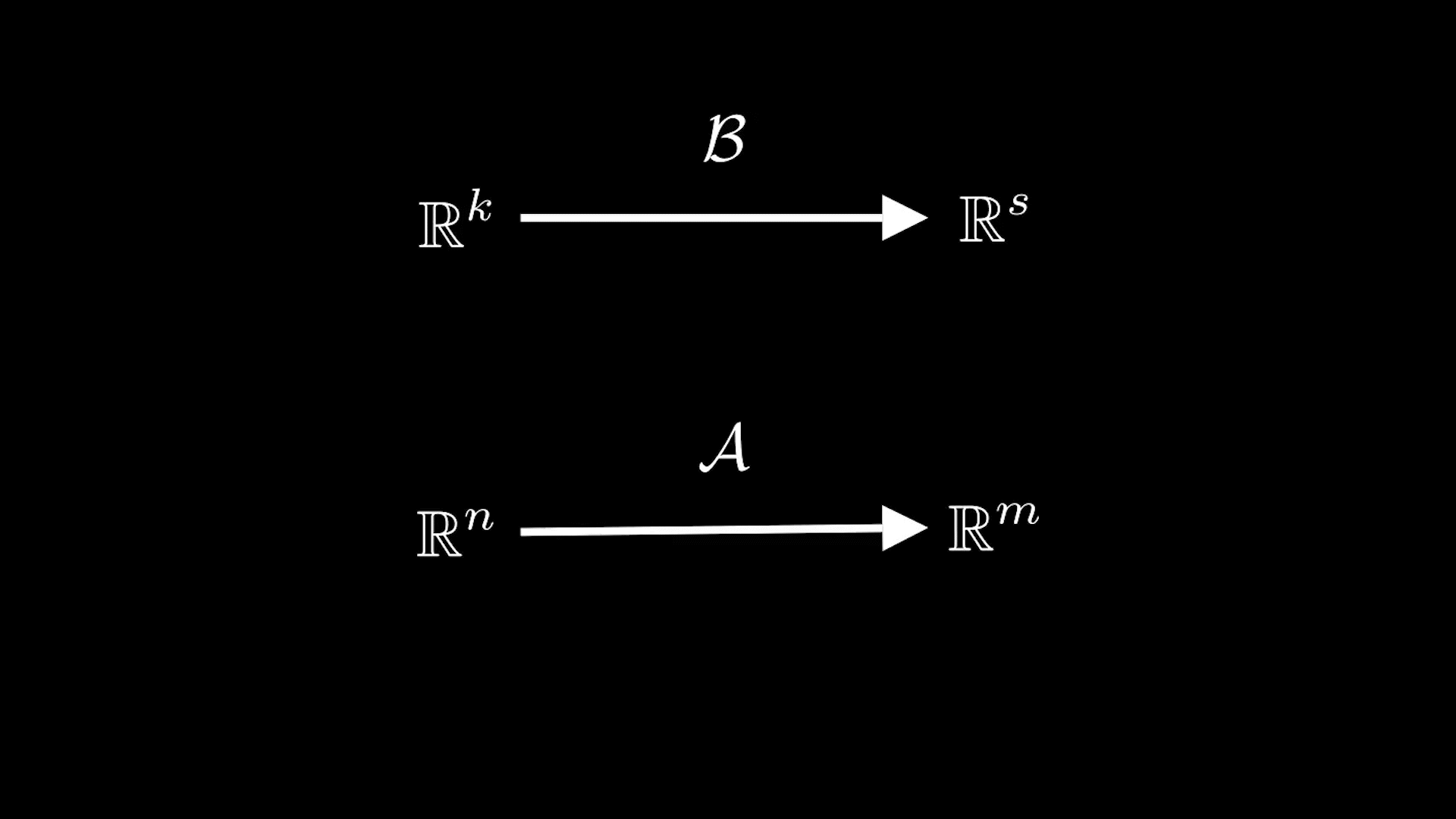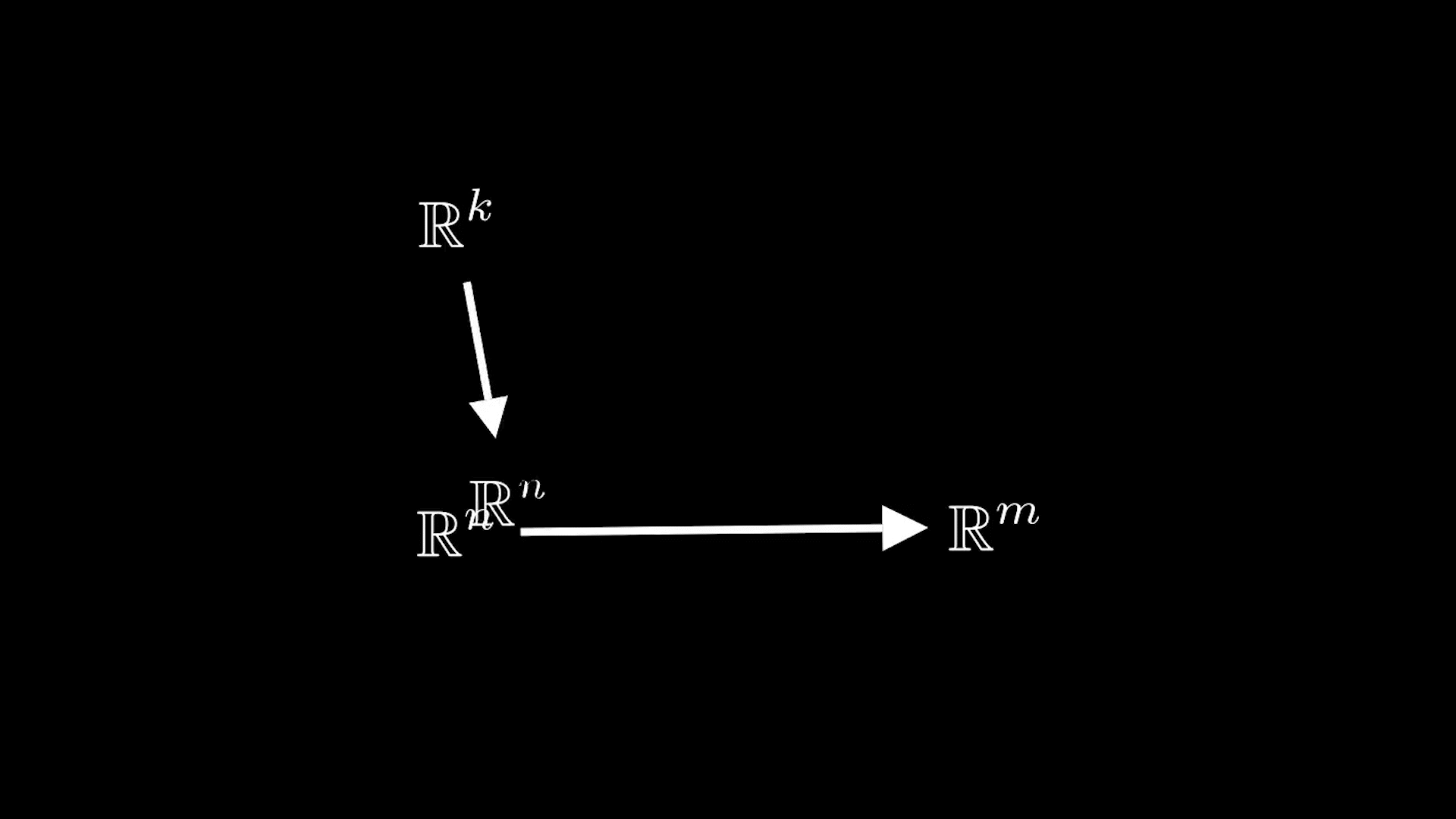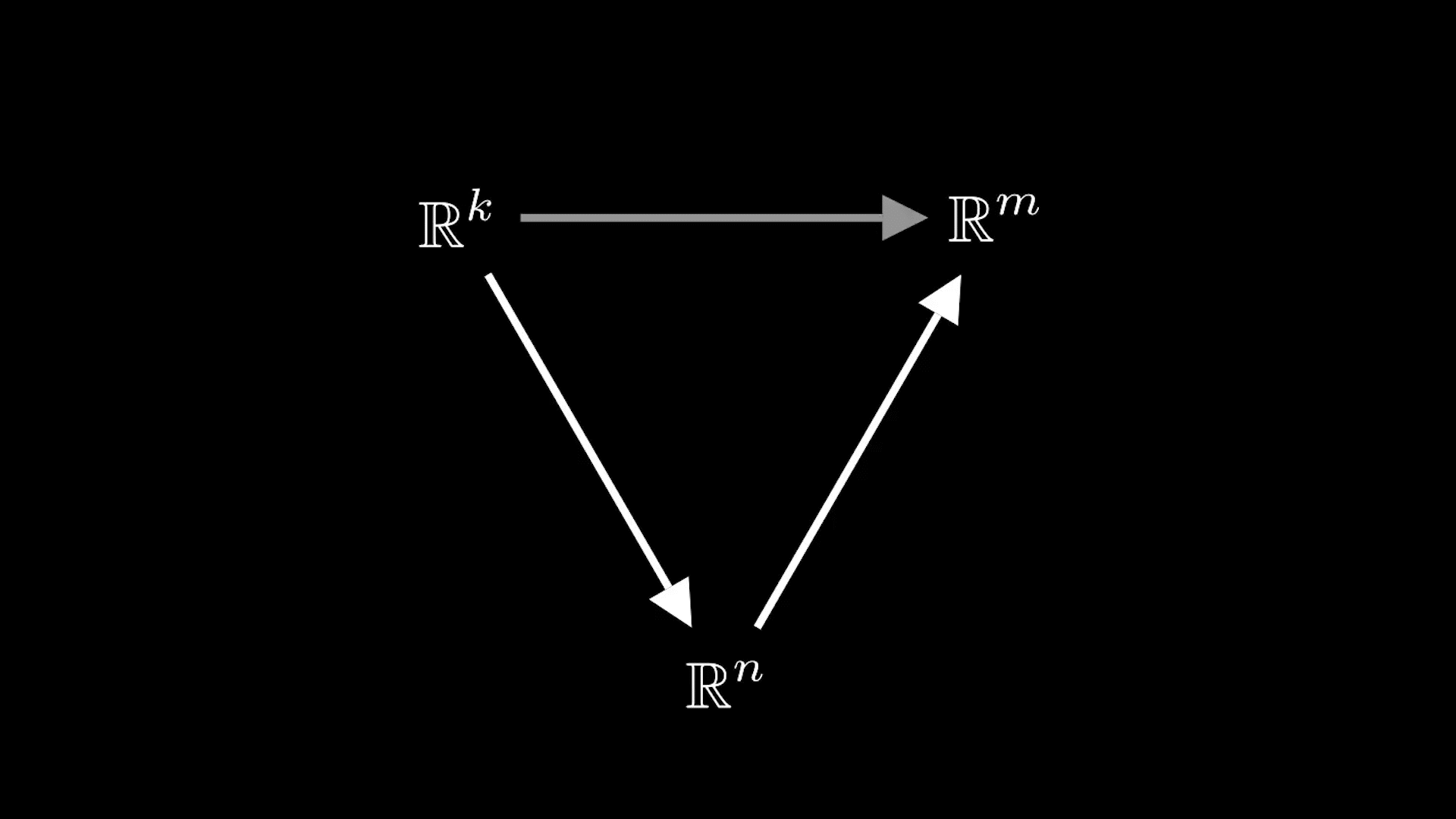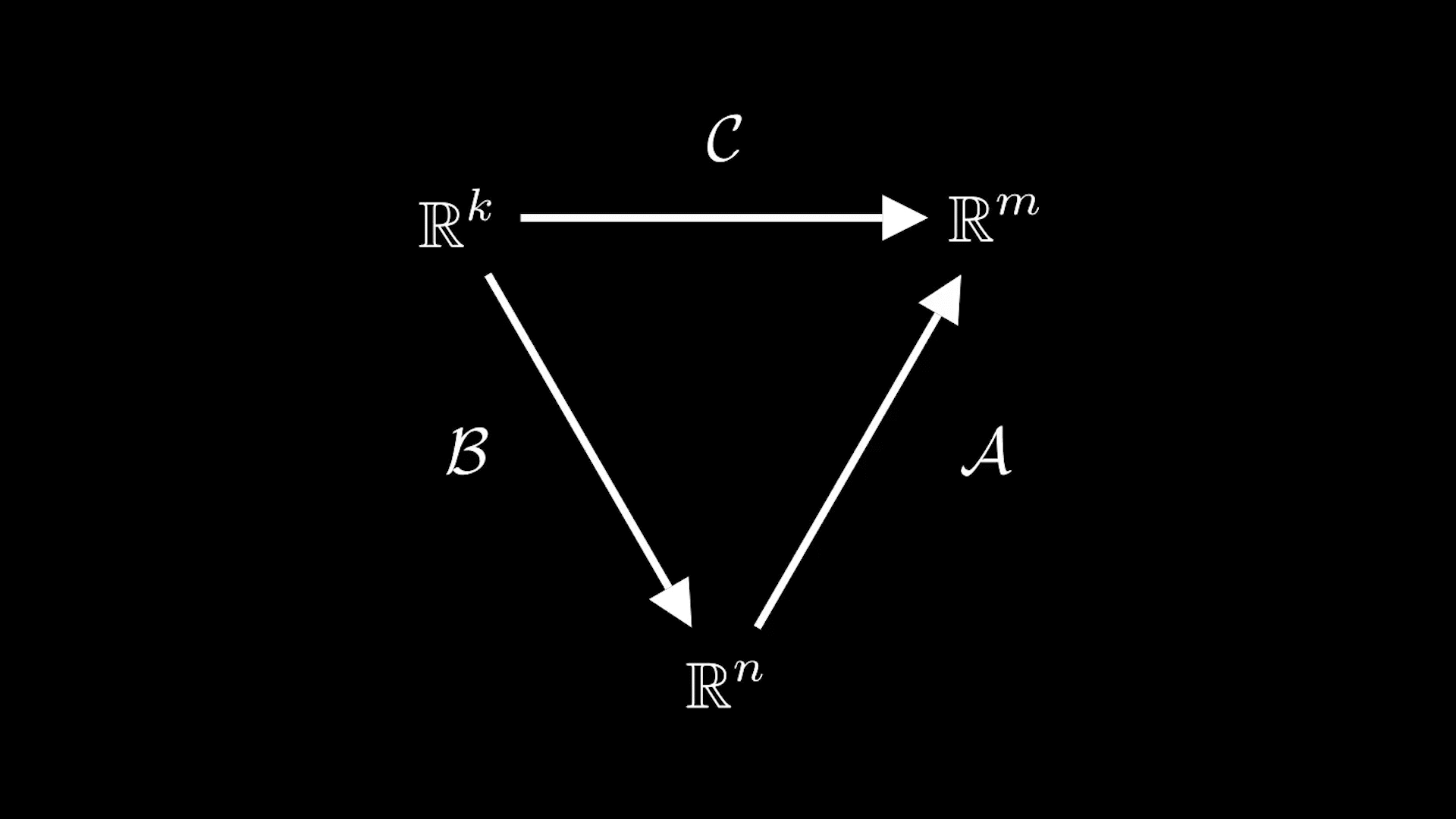
Рассмотрим линейные отображения\mathcal{A}и\mathcal{B}

\mathcal{A} : \mathbb{R}^m \rightarrow \mathbb{R}^s, \quad \mathcal{B} : \mathbb{R}^n \rightarrow \mathbb{R}^m,

и их композицию \mathcal{C}

\mathcal{C} = \mathcal{A} \circ \mathcal{B}.

Легко проверяется, что \mathcal{C} будет линейным отображением

\mathcal{C}(\lambda_1x+\lambda_2y)= (\mathcal{A} \circ \mathcal{B})(\lambda_1x+\lambda_2y)= \mathcal{A}(\mathcal{B}(\lambda_1x)+\mathcal{B}(\lambda_2y))=\mathcal{A}(\lambda_1\mathcal{B}x+\lambda_2\mathcal{B}y)= \\ = \lambda_1\mathcal{A}(\mathcal{B}x)+\lambda_2\mathcal{A}(\mathcal{B}y)=\lambda_1\mathcal{C}x+\lambda_2\mathcal{C}y.

Поэтому, если зафиксировать в \mathbb{R}^n, \mathbb{R}^mи \mathbb{R}^sбазисы, то каждому линейному отображению можно поставить в соответствие его матрицу

\mathcal{A} \mapsto A, \quad \mathcal{B} \mapsto B, \quad \mathcal{C} \mapsto C.

Нас теперь интересует, как между собой они связаны. Для этого рассмотрим следующее равенство

(\mathcal{A} \circ \mathcal{B})x =\mathcal{A}(\mathcal{B}(x)) = \mathcal{A}y = z

и найдём координаты вектораz через координаты вектора x.

Так как\mathcal{A}y=z,то

z_i=\sum_{k=1}^{m}a_{ik}y_k, \quad i =1,\ldots,s.

Но из равенстваy= \mathcal{B}xследует, что

y_k=\sum_{j=1}^{n}b_{kj}x_j, \quad k = 1,\ldots,m.

Подставляем в равенство выше и получаем

z_i=\sum_{k=1}^{m}a_{ik}y_k= \sum_{k=1}^{m}a_{ik}\sum_{j=1}^{n}b_{kj}x_j=\sum_{j=1}^{n}(\sum_{k=1}^{m}a_{ik}b_{kj})x_j, \quad i =1,\ldots,s.

С другой стороны, (\mathcal{A} \circ \mathcal{B})x = \mathcal{C}x=z,то есть

z_i= \sum_{j=1}^{n}c_{ij}x_j, \quad i = 1,\ldots,s.

Сравнивая первое и второе равенство для координатz,получаем такое соотношение

c_{ij}=\sum_{k=1}^{m}a_{ik}b_{kj} \quad (i=1,\ldots,s;\,j=1,\ldots,n),

которое является формулой умножения матрицы на матрицу.

Таким образом, умножение матрицы на матрицу вводится исходя из того, как действует композиция линейных отображений.

Другими словами, если линейным отображениям\mathcal{A}и\mathcal{B}поставить в соответствие их матрицыAиB,то композиции этих отображений\mathcal{A} \circ \mathcal{B}ставится в соответствие матрица, которая является произведением матрицAB.

Отсюда, кстати, следует, что матрицыAиBможно умножить только тогда, когда число столбцов матрицыAравно числу строк матрицыB.

343b6133d40b7552569a3a125c3295ce.gif

Пусть A— матрица размера m \times n,, а B— матрица размера s\times k.Тогда, если в пространствах \mathbb{R}^n,\mathbb{R}^m,\mathbb{R}^kи \mathbb{R}^sзафиксировать базисы, то этим матрицам ставятся в соответствие линейные отображения\mathcal{A}и\mathcal{B}

\mathcal{A}:\mathbb{R}^n \rightarrow \mathbb{R}^m,\quad \mathcal{B}: \mathbb{R}^k \rightarrow \mathbb{R}^{s}.

Но композиция \mathcal{A} \circ \mathcal{B}определена только тогда, когда s=n,то есть число столбцов матрицыAравно числу строк матрицыB.

Заключение

Таким образом, умножение матриц вводится исходя из того, как действуют линейные отображения. И это намекает на некую связь между ними.

Ниже оставлю различные учебники по алгебре, где можно про всё это прочитать более подробное, и другие различные источники.

Ссылки на литературу и различные источники

Основное:

[1] Введение в алгебру. В 3 частях. Часть 1. Основы алгебры. Кострикин А.И.

Дополнительное:

[1] Введение в алгебру. В 3 частях. Часть 2. Линейная алгебра. Кострикин А.И.

[2] Линейная алгебра и геометрия, Кострикин А.И., Манин Ю.И.

Прочее:

Для создания графики использовался manimCE:  https://github.com/manimCommunity/manim

Кому интересно, то вот видео к статье:

© Habrahabr.ru