Планирование экспедиции. Геодезия и отвага
Это продолжение истории Экваториальной Градусной экспедиции в XVIII веке отправившейся к, как следует из названия, экватору, чтобы уточнить форму Земли.
Нашу научную экспедицию к берегам Перу мы оставили в том месте, где морской министр Франции, выделивший государственный бюджет на проект, пришел в ужас от кадровой политики ученых и сам занялся подбором персонала, выделением кредитов и денег, а также дипломатической перепиской с испанским двором. Луи Годену, как идеологу, оставалось лишь позаботиться о плане работ и инструментах.
Планирование работ
Аллегория к предварительному планированию. «Геометрия», Корнелис Корт, 1565 (https://www.rijksmuseum.nl/)
Планирование работ происходило в публичном пространстве кофеен и трактиров, широко обсуждалось в уже упомянутом нами Градо и в личной переписке всей ученой братии. Над чашками и бокалами разворачивались карты (довольно устаревшие) и шли ожесточенные споры.
Луи Годен, руководитель, ослепленный легким успехом, заявляет о том, что лучше измерить длину не 1 градуса меридиана (около 111 км), а целых четырех. Определенный смысл в этом действительно есть: чем большее расстояние мы измеряем, тем больше мы в безопасности от влияния случайных погрешностей. Но четыре градуса! Почти четыре с половиной сотни километров в малоизученном высокогорье, на которое и карт-то толком нет!
Красным помечена предлагаемая к измерению дуга меридиана.
В чем заключалась задача экспедиции? Требовалось измерить длину дуги меридиана в 1 градус на экваторе и сравнить, на сколько туазов (это местная мера длины) она отличается от 1 градуса Парижского меридиана.
На злобу дня в Академию пришло едкое письмо из России, где в самом вежливом тоне Жозеф Делилль, создатель Санкт-Петербургской обсерватории, предложил коллеге не мелочиться и, чего уж, измерить дугу меридиана до самой Огненной Земли. Чтобы дважды не ходить. Впрочем, Делилль имел право быть сколько угодно резким: Годен был его учеником.
«Осип Николаевич» Делилль (отец российской астрономии), гравюра Конрада Вестрмайра, Википедия).
Маленькая историческая справка
В 1735 году, о котором мы говорим, в России царствовала Анна Иоановна, племянница Петра I: Екатерина I уже умерла, а ее дочь Елизавета еще не захватила престол. Кстати, если вы окажетесь в Москве, сходите поглядеть на Царь-колокол. Когда Луи Годен готовил свою экспедицию, Царь-колокол отливали в Кремле в специально подготовленной яме. А в Академии Наук Петербурга за астрономию отвечал Жозеф Николя Делилль, приглашенный из Парижа еще Петром I.
Делилль совершенно легендарный дядька. Учился он у Джованни Кассини, итальянца, стоявшего во главе первой обсерватории Парижа. Потом уехал в Россию делать обсерваторию в Петербурге. Тогда она размещалась в здании Кунсткамеры. Он закупил приборы, написал план обучения молодых астрономов, организовал регулярные метеоизмерения, предложил основать службу времени. Кстати, в Кунсткамере в экспозиции «Первая обсерватория» демонстируются те самые заказанные им инструменты. По предложению Делилля, при Академии Наук был создан Географический департамент для руководства картографированием. Страна большая, карты на эту огромную территорию надо создавать, а существующие — обновлять. Более того, Делилль придумал коническую проекцию, как раз для нашей территории подходящую.
Про проекции хочу немного пояснить
Помните старую шутку:
Никто не сделал больше для величия России, чем проекция Меркатора.
Судя по общественному резонансу, слишком многие приняли изящный юмор за чистую монету. Дело в том, что нельзя просто так взять и перенести (земной) шар (мы же еще про XVIII век) на плоскость.
Цилиндрическая проекция Меркатора из https://gisgeography.com/cylindrical-projection/
Выше картинка цилиндрической проекции Меркатора Проекция — это математический способ перенести изображение с земного шара на плоскую карту с контролируемым искажением углов и расстояний. Идея проста: земной шар мы оборачиваем бумажным цилиндром, и в месте соприкосновения (это может быть экватор, как на картинке, или меридиан) длина линии (например, дороги) на шаре будет равна длине линии на бумаге. Чем дальше от места касания — тем больше при переносе на бумагу будут искажены длины линий. Поперечная проекция Меркатора (когда цилиндр касается Земного шара по меридиану) — сегодня самая популярная из проекций.
Россия, однако, далеко от экватора и вытянута с востока на запад. Получаются сплошные искажения. Поэтому Делилль в своем XVIII веке придумал специальный подвид конической проекции.
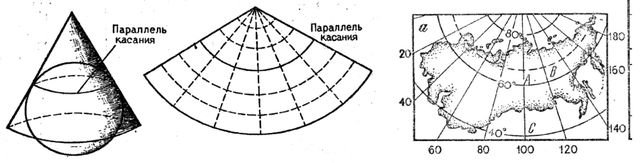Коническая проекция из «В.Н. Попов, С.И. Чекалин. Геодезия: Учебник для вузов.- М.: «Горная книга», 2007.»
Тут земной шар оборачивается конусом, а значит «соприкосновение» бумаги с шаром идет по параллели. Профит: меньше искажений на нашу большую территорию.
Почему Делилль молодец и про проекции надо помнить? Во-первых, до конца ХХ века по бумажным картам выполняли измерения: определяли длины и площади. И подготовка любого путешествия велась по картам. Не учел искажение — не заложил денег и провианта — погиб в пути. Сейчас проекции тоже существуют, хотя обычный пользователь редко сталкивается с ними напрямую. А вот косвенно — еще как. Дело в том, что координаты, которые измеряет GPS-приемник (при обмере приусадебного участка, для постановки на учет, например) — пространственные и относятся к тому самому Земному шару (на самом деле, эллипсоиду). А координаты, которые фигурируют в документах на собстенность — плоские. Относящиеся к поперечно цилиндрической проекции шара на плоскость. И, чтобы пересчитать одно в другое, надо не только помнить о том, что пересчет необходим, но и помнить, с какой точностью выведены те формулы, которые заложены в программу пересчета.
Кстати, Делилль тоже пытался заниматься градусными измерениями: года через два после Луи Годена. Но ему сократили финансирование, поскольку для нашей страны эта сугубо научная (как тогда казалось) задача не была первостепенной. Увы, карьера ученого в Петербурге завершилась бесславно. Он оказался замешан в шпионском скандале (то ли правда было за что, а то ли политическая борьба за место директора обсерватории) и вернулся в Париж к 1747 году. Зато в России весь XVIII век для измерения температуры использовали градусы Делилля. Но вернемся к основному повествованию.
Как измерить длину дуги меридиана?
Что именно собирались делать ученые, когда доберутся до тайного города Кито, что в Перу? Помните, мы уже говорили об Эратосфене и градусных измерениях? Градусные измерения — это когда между двумя точками, расположенными на одном меридиане, измеряют расстояние и разность широт.
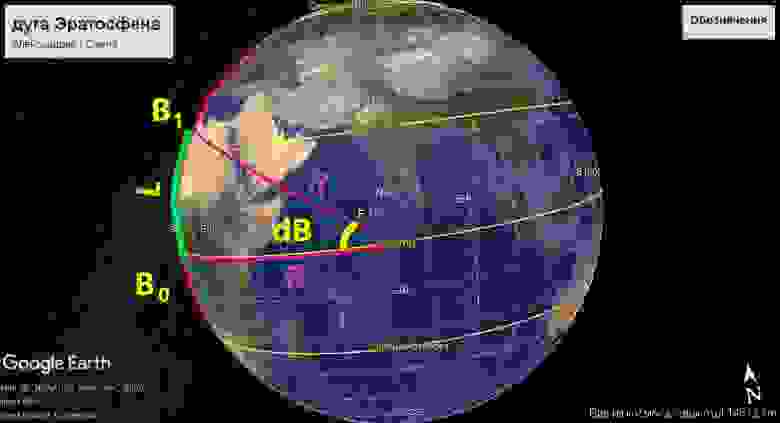Градусные измерения Эратосфена: известно расстояние L в линейной мере и градусной: разность широт между точками.
Про измерение расстояния: к XVIII веку (и, кстати, до конца века двадцатого) для этой цели применялся метод триангуляции. Как следует из названия — она имеет отношение к треугольникам.
Как триангуляция появилась в геодезии?
Был такой голландский ученый, живший в XVI веке, Эратосфен Батавский (в те времена было принято брать себе хвастливые прозвища, подражая ученым древности), он же Виллеборд Снелл. Именно он использовал и популяризировал известную из математики триангуляцию для геодезических работ.
Подобно Эратосфену, Снелл тоже выполнял градусные измерения для определения радиуса Земли. Ему тоже нужно было найти длину дуги меридиана в градусах и в линейной мере (милях, к примеру). Однако караванов с погонщиками в северной Европе не было, так что расстояние пришлось определять самостоятельно.
Как устроена триангуляция?
Предположим, мы хотим найти расстояние между весьма удаленными точками (допустим удаленных на 100 километров). Просто измерить это расстояние невозможно: нет прямой видимости, нет возможности хотя бы построить прямую линию между точками (ведь одна может находиться на холме, а другая на низменности, между ними могут быть реки, овраги и озера. На помощь приходит цепочка треугольников.
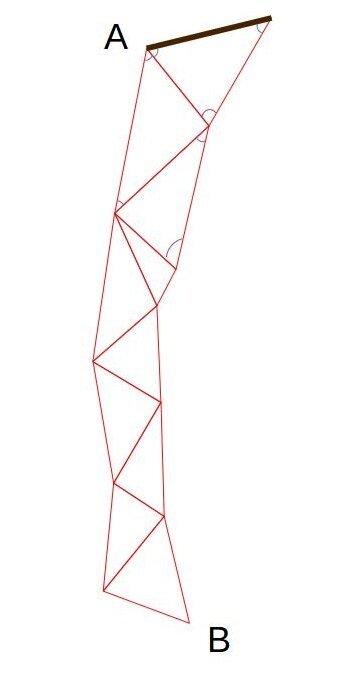Это звено триангуляции АВ
Допустим, нам нужно найти расстояние (АВ). Мы строим цепочку стыкующихся треугольников вокруг этой линии и измеряем небольшую (до 10 км) сторону треугольника A-1.
Фрагмент триангуляции. А-1 — измеренная сторона (базис).
Измеренная сторона на рисунке помечена коричневым. Дальше мы угломерным прибором (квадрантом, астролябией, тахеометром) измеряем все внутренние углы треугольника 1-А-2. Получается, нам известны одна сторона и углы в треугольнике. Значит мы можем вычислить оставшиеся стороны в треугольнике. Среди прочего — мы найдем сторону А-2. И, если мы измерим все углы в треугольнике А-2–3, то сможем найти все стороны и для него тоже. Таким образом, последовательно решая стыкующиеся треугольники, для которых известны внутренние углы, мы сможем отыскать длины сторон всех треугольников.
Тут возникает нестыковка: мы можем отыскать все элементы треугольника по стороне и всего лишь двум углам. Значит, измерять все углы нет необходимости, достаточно измерить только два из трех? Теоретически это так. Однако на практике измеряют третий угол, чтобы обеспечить избыточность измерений. Как минимум — это такой простейший контроль: если сумма всех углов не будет равна 180 градусам — где-то в измерения вкралась серьезная ошибка.
Существуют статистические методы (курс ТМОГИ), позволяющие оценить погрешность, с которой были выполнены измерения и вычисления окончательной величины (расстояния), но в первой трети XVIII века, о которой я рассказываю, про все это имелись скорее смутные догадки.
Примерно по такой схеме, как описана выше, строил свои рассуждения Снелл. Он измерил расстояние от своего дома до шпиля местной церкви, а затем построил цепочку стыкующихся треугольников (триангуляции), которая позволила ему определить расстояние между городами Алкмар и Берген-оп-Зом, которые лежат на одном меридиане. Далее, зная длину дуги меридиана в линейной мере (милях) и в градусной мере — он мог вычислить радиус Земли, подобно Эратосфену (настоящему Эратосфену, Киренскому).
Метод Снелла оказался удачным, выполнимым и был взят на вооружение. Разумеется, по мере применения он совершенствовался: измерения выйдут точнее, если треугольники будут, по возможности, равносторонние или хотя бы равнобедренные. Придумали также делать дополнительный базис (измерять еще одну сторону треугольника где-то в конце цепочки) — для контроля. Эта сторона треугольника будет известна из измерений и из вычислений. Разница поможет оценить погрешность, с которой проводились работы.
Кстати, триангуляция была основным методом высокоточных геодезических измерений до самого конца XX века, пока не появились спутниковые системы позиционирования, GPS/ГЛОНАСС. Но это уже — совсем другая история.
Современный (конец ХХ века) пункт триангуляции в Тульской области.
Вернемся к Экваториальной экспедиции 1735 года. Что именно предстояло сделать ученым?
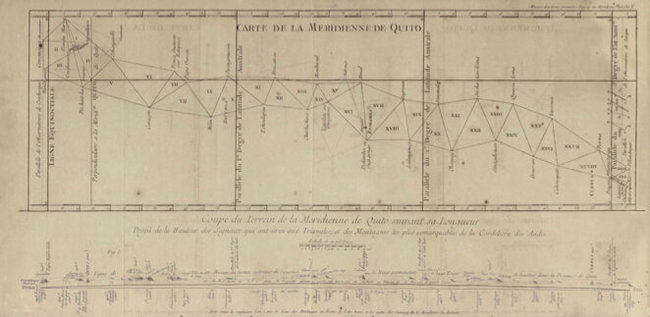Схема триангуляции из журнала Лакондамина.
Ученые решают разбить вдоль меридиана (с севера на юг) цепочку треугольников. Треугольники требуется делать по возможности равносторонними или хотя бы равнобедренными, на местности необходимо обеспечить видимость хотя бы на две соседние вершины. Учитывая расстояния и сложности местного рельефа, треугольников по плану двадцать семь. Длина стороны в них около 30–40 км.
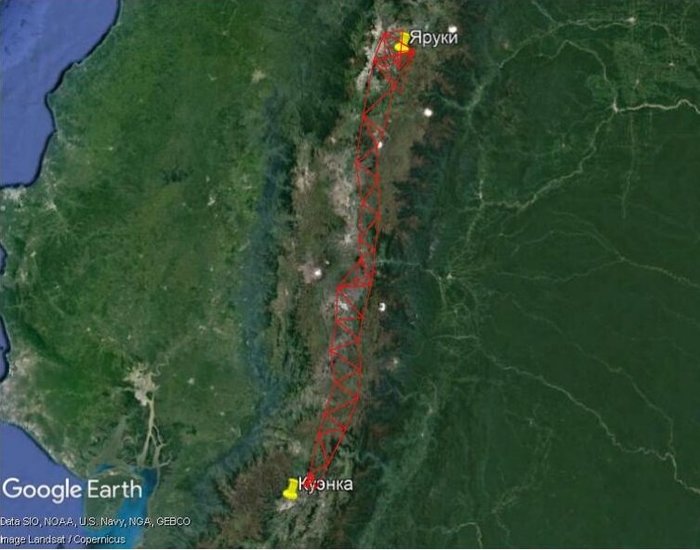На современную карту тут наложены треугольники перуанской экспедиции (примерный экскиз)
Измерена будет сторона одного из северных треугольников (базис в районе Яркуи) и еще одна сторона на юге (базис в Куэнке), для контроля результатов. К сожалению, ввиду того, что это горная цепь с ущельями, скалами, реками и провалами, удобное плато для базиса было найти трудно, поэтому его длина существенно меньше (раза в четыре), чем длины сторон основных треугольников. Базис составит около 12 км. Во всех прочих треугольниках будут измерены внутренние углы. После этого ученые последовательно вычислят длины сторон всех треугольников.
Казалось бы: как теперь из наклонных сторон треугольников получить длину меридиана? Ученые будут вычислять длину проекции каждой западной стороны треугольника на меридиан. В сумме они дадут длину дуги меридиана:
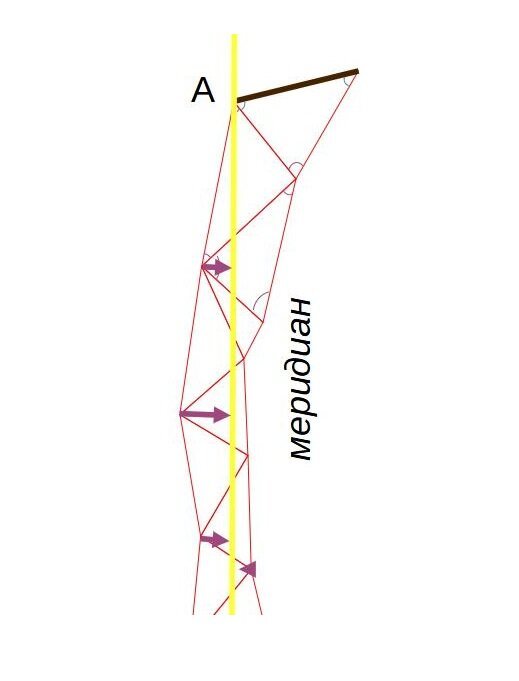Искомую длину меридиана вычисляли по сумме проекций сторон треугольника на меридиан
Кстати, вот любопытный факт про измеряемую сторону треугольника (базис, как он называется в триангуляции):
Деллиль в России (и еще кое-то из его коллег в Швеции) считал, что удобно будет измерять базис по замерзшему льду реки или залива, поскольку он образует ровную, поверхность с идеальной видимостью. Очень крутая и новаторская по тем временам мысль. Увы, замерзающих заливов в Перу не было.
Тот план, который Годен изначально представил в Академии, касался измерений в горной долине между западной и восточной цепью Анд. Это казалось разумным: горные вершины послужат отличным ориентиром для наблюдений, а города Кито (на севере) и Куэнка (на юге), упомянутые на карте, должны иметь хоть какие-то подъездные дороги. Однако потом Годен увлекся идеей измерять не меридиан, а параллель, его коллеги вообще хотели держаться ближе к побережью, так что планирование миссии застопорилось и окончательный ответ на вопрос «а что именно мы там будем делать?» не был дан до самого отплытия из Франции.
«Удобная для измерений» горная долина Кито, Википедия.
В защиту такого подхода руководителя миссии следует сказать, что предварительная подготовка работ велась по очень приблизительным картам, самой свежей из которых было лет двадцать. Последним французом, побывавшим в Перу был Амеде Франсуа Фрезье (торговец, инженер и шпион).
Картматериалы из «Описания путешествия» Фрезье, 1712 г.
Любопытно, что широко известен он совсем не разведдеятельностью, а клубничным десертом. Именно он привез чилийскую землянику в в королевскую оранжерею. И свое французское имя fraise, ананасная земляника, ее потомок, носит по его фамилии. В общем, планирование экспедиции, хотя и было занимательным, содержало слишком много белых пятен. Все станет понятно на местности. А пока следовало позаботиться об инструментах.
Предыдущие статьи этого цикла:
О форме Земли: тыква или дыня?
Как набрать команду к экватору?
