Пережевывая логистическую регрессию28.01.2020 14:54

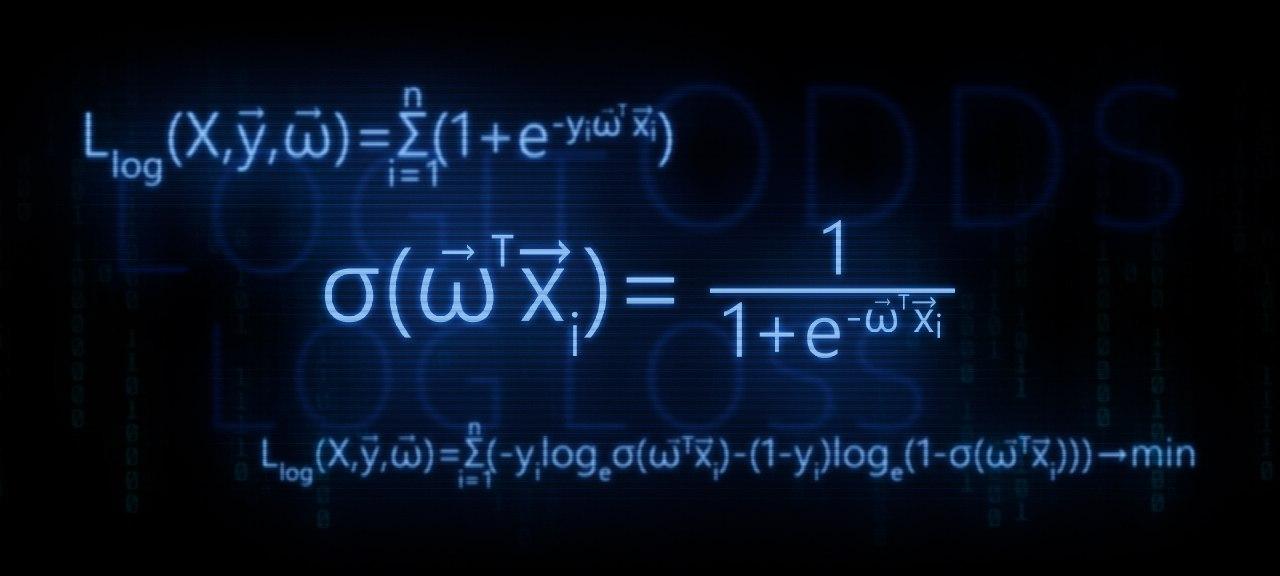
В этой статье, мы будем разбирать теоретические выкладки преобразования функции линейной регрессии в функцию обратного логит-преобразования (иначе говорят, функцию логистического отклика). Затем, воспользовавшись арсеналом метода максимального правдоподобия, в соответствии с моделью логистической регрессии, выведем функцию потерь Logistic Loss, или другими словами, мы определим функцию, с помощью которой в моделе логистической регрессии подбираются параметры вектора весов $\vec{w}$ .

План статьи:

1. Повторим о прямолинейной зависимости между двумя переменными
2. Выявим необходимость преобразования функции линейной регрессии $f(w,x_i) = \vec{w}^T \vec{x_i}$ в функцию логистического отклика $\sigma(\vec{w}^T \vec{x_i}) = \frac{1}{1+e^{-\vec{w}^T \vec{x_i}}}$
3. Проведем преобразования и выведем функцию логистического отклика
4. Попытаемся понять, чем плох метод наименьших квадратов при подборе параметров $\vec{w}$ функции Logistic Loss
5. Используем метод максимального правдоподобия для определения функции подбора параметров $\vec{w}$ :

5.1. Случай 1: функция Logistic Loss для объектов с обозначением классов 0 и 1:

$L_{log}(X,\vec{y},\vec{w}) = \sum\limits_{i=1}^n(-y_i \mkern 2mu log_e \mkern 5mu \sigma(\vec{w}^T \vec{x_i}) - (1-y_i) \mkern 2mu log_e \mkern 5mu (1 - \sigma(\vec{w}^T \vec{x_i})) ) \rightarrow min$

5.2. Случай 2: функция Logistic Loss для объектов с обозначением классов -1 и +1:

$L_{log}(X,\vec{y},\vec{w}) = \sum\limits_{i=1}^n \mkern 2mu log_e \mkern 5mu (1+e^{-y_i\vec{w}^T\vec{x_i}}) \rightarrow min$

Статья изобилует простыми примерами, в которых все расчеты легко произвести устно или на бумаге, в некоторых случаях может потребоваться калькулятор. Так что подготовьтесь :)

Данная статья в большей мере рассчитана на датасайнтистов с начальным уровнем познаний в основах машинного обучения.

В статье также будет приведен код для отрисовки графиков и расчетов. Весь код написан на языке python 2.7. Заранее поясню о «новизне» используемой версии — таково одно из условий прохождения известного курса от Яндекса на не менее известной интернет-площадке онлайн образования Coursera, и, как можно предположить, материал подготовлен по мотивам этого курса.

01. Прямолинейная зависимость

Вполне резонно задать вопрос — причем здесь прямолинейная зависимость и логистическая регрессия?
Все просто! Логистическая регрессия представляет собой одну из моделей, которые относятся к линейному классификатору. Простыми словами, задачей линейного классификатора является предсказание целевых значений $y$ от переменных (регрессоров) $X$ . При этом считается, что зависимость между признаками $X$ и целевыми значениями $y$ линейная. Отсюда собственно и название классификатора — линейный. Если очень грубо обобщить, то в основе модели логистической регрессии лежит предположение о наличии линейной зависимости между признаками $X$ и целевыми значениями $y$ . Вот она — связь.

В студии первый пример, и он, правильно, о прямолинейной зависимости исследуемых величин. В процессе подготовки статьи наткнулся на пример, набивший уже многим оскомину — зависимость силы тока от напряжения («Прикладной регрессионный анализ», Н.Дрейпер, Г.Смит). Здесь мы его тоже рассмотрим.

В соответствии с законом Ома:

$I = U/R$ , где $I$ — сила тока, $U$ — напряжение, $R$ — сопротивление.

Если бы мы не знали закон Ома, то могли бы найти зависимость эмпирически, изменяя $U$ и измеряя $I$ , поддерживая при этом $R$ фиксированным. Тогда мы бы увидели, что график зависимости $I$ от $U$ дает более или менее прямую линию, проходящую через начало координат. Мы сказали «более или менее», так как, хотя зависимость фактически точная, наши измерения могут содержать малые ошибки, и поэтому точки на графике, возможно не попадут строго на линию, а будут разбросаны вокруг нее случайным образом.

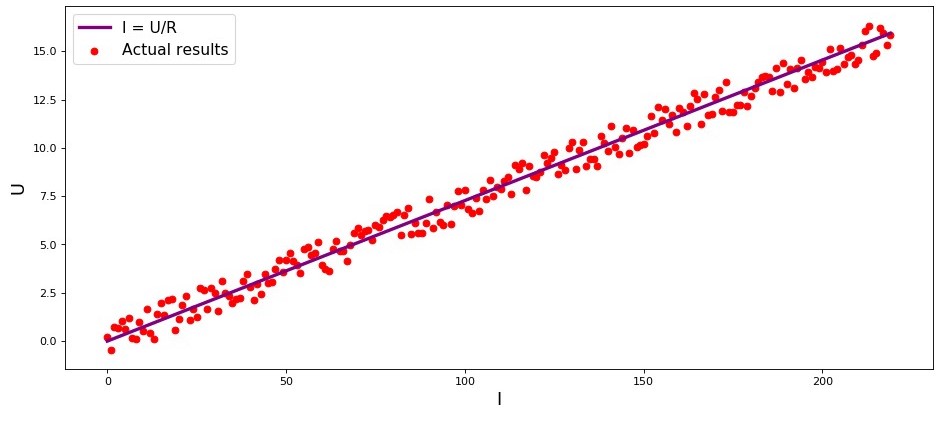
График 1 «Зависимость $I$ от $U$ »

Код отрисовки графика

import matplotlib.pyplot as plt
%matplotlib inline

import numpy as np

import random

R = 13.75

x_line = np.arange(0,220,1)
y_line = []
for i in x_line:
    y_line.append(i/R)
    
y_dot = []
for i in y_line:
    y_dot.append(i+random.uniform(-0.9,0.9))


fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R')
plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results')
plt.xlabel('I', size = 16)
plt.ylabel('U', size = 16)
plt.legend(prop = {'size': 14})
plt.show()

02. Необходимость преобразований уравнения линейной регрессии

Рассмотрим очередной пример. Представим, что мы работаем в банке и перед нами задача определить вероятность возврата кредита заемщиком в зависимости от некоторых факторов. Для упрощения задачи, рассмотрим только два фактора: месячная зарплата заемщика и месячный размер платежа на погашение кредита.

Задача очень условная, но на этом примере мы сможем понять, почему для ее решения недостаточно применения функции линейной регрессии, а также узнаем какие преобразования с функцией требуется провести.

Возвращаемся к примеру. Понято, что чем выше зарплата, тем больше заемщик сможет ежемесячно направлять на погашение кредита. При этом, для определенного диапазона зарплат эта зависимость будет вполне себе линейная. Например, возьмем диапазон зарплат от 60.000Р до 200.000Р и предположим, что в указанном диапазоне заработных плат, зависимость размера ежемесячного платежа от размера заработной платы — линейная. Допустим, для указанного диапазона размера заработных плат было выявлено, что соотношение зарплаты к платежу не может опускаться ниже 3 и еще у заемщика должно оставаться в запасе 5.000Р. И только в таком случае, мы будем считать, что заемщик вернет кредит банку. Тогда, уравнение линейной регрессии примет вид:

$f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2},$

где $w_0 = -5.000$ , $w_1 = 1$ , $w_2 = -3$ , $x_{i1}$ — зарплата $i$ -го заемщика, $x_{i2}$ — платеж по кредиту $i$ -го заемщика.

Подставляя в уравнение зарплату и платеж по кредиту с фиксированными параметрами $\vec{w}$ можно принять решение о выдаче или отказе кредита.

Забегая вперед, отметим, что, при заданных параметрах $\vec{w}$ функция линейной регрессии, применяемая в функции логистичиеского отклика будет выдавать большие значения, которые затруднят проведение расчетов по определению вероятностей погашения кредита. Поэтому, предлагается уменьшить наши коэффициенты, скажем так, в 25.000 раз. От этого преобразования в коэффициентах, решение о выдачи кредита не изменится. Запомним этот момент на будущее, а сейчас чтобы было еще понятнее, о чем речь, рассмотрим ситуация с тремя потенциальными заемщиками.

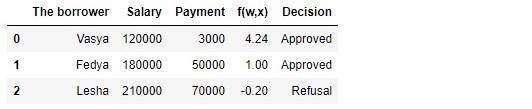
Таблица 1 «Потенциальные заемщики»

Код для формирования таблицы

import pandas as pd

r = 25000.0
w_0 = -5000.0/r
w_1 = 1.0/r
w_2 = -3.0/r

data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 
        'Salary':np.array([120000,180000,210000]),
       'Payment':np.array([3000,50000,70000])}

df = pd.DataFrame(data)

df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2

decision = []
for i in df['f(w,x)']:
    if i > 0:
        dec = 'Approved'
        decision.append(dec)
    else:
        dec = 'Refusal'
        decision.append(dec)
        
df['Decision'] = decision

df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]

В соответствии с данными таблицы, Вася при зарплате в 120.000Р хочет получить такой кредит, чтобы ежемесячного гасить его по 3.000Р. Нами было определено, что для одобрения кредита, размер заработной платы Васи должен превышать в три раза размер платежа, и чтобы еще оставалось 5.000Р. Этому требованию Вася удовлетворяет: $120.000-3 * 3.000-5.000 = 106.000$ . Остается даже 106.000Р. Несмотря на то, что при расчете $f(w,x_i)$ мы уменьшили коэффициенты $\vec{w}$ в 25.000 раз, результат получили тот же — кредит может быть одобрен. Федя тоже получит кредит, а вот Леше, несмотря на то, что он получает больше всех, придется поумерить свои аппетиты.

Нарисуем график по такому случаю.

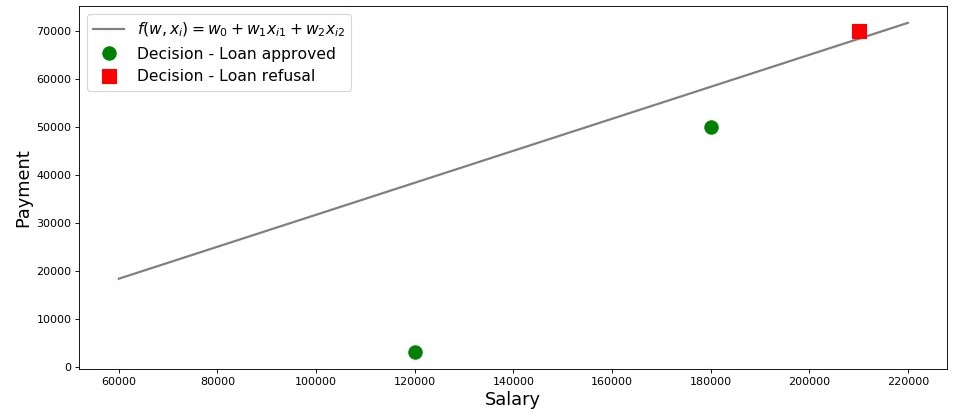
График 2 «Классификация заемщиков»

Код для отрисовки графика

salary = np.arange(60000,240000,20000)
payment = (-w_0-w_1*salary)/w_2


fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$')
plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 
         'o', color ='green', markersize = 12, label = 'Decision - Loan approved')
plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 
         's', color = 'red', markersize = 12, label = 'Decision - Loan refusal')
plt.xlabel('Salary', size = 16)
plt.ylabel('Payment', size = 16)
plt.legend(prop = {'size': 14})
plt.show()

Итак, наша прямая, построенная в соответствии с функцией $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ , отделяет «плохих» заемщиков от «хороших». Те заемщики, у кого желания не совпадают с возможностями находятся выше прямой (Леша), те же, кто способен согласно параметрам нашей модели, вернуть кредит, находятся под прямой (Вася и Федя). Иначе можно сказать так — наша прямая разделяет заемщиков на два класса. Обозначим их следующим образом: к классу $+1$ отнесем тех заемщиков, которые скорее всего вернут кредит, к классу $-1$ или $0$ отнесем тех заемщиков, которые скорее всего не смогут вернуть кредит.

Обобщим выводы из этого простенького примера. Возьмем точку $M(x_1,x_2)$ и, подставляя координаты точки в соответствующее уравнение прямой $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ , рассмотрим три варианта:

1. Если точка находится под прямой, и мы относим ее к классу $+1$ , то значение функции $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ будет положительным от $0$ до $+\infty$ . Значит мы можем считать, что вероятность погашения кредита, находится в пределах $(0.5,1]$ . Чем больше значение функции, тем выше вероятность.

2. Если точка находится над прямой и мы относим ее к классу $-1$ или $0$ , то значение функции будет отрицательным от $0$ до $-\infty$ . Тогда мы будем считать, что вероятность погашения задолженности находится в пределах $[0,0.5)$ и, чем больше по модулю значение функции, тем выше наша уверенность.

3. Точка находится на прямой, на границе между двумя классами. В таком случае значение функции $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ будет равно $0$ и вероятность погашения кредита равна $0.5$ .

Теперь, представим, что у нас не два фактора, а десятки, заемщиков не три, а тысячи. Тогда вместо прямой у нас будет m-мерная плоскость и коэффициенты $w$ у нас будут взяты не с потолка, а выведены по всем правилам, да на основе накопленных данных о заемщиках, вернувших или не вернувших кредит. И действительно, заметьте, мы сейчас отбираем заемщиков при уже известных коэффициентах $w$ . На самом же деле, задача модели логистической регрессии как раз и состоит в том, чтобы определить параметры $w$ , при которых значение функции потерь Logistic Loss будет стремиться к минимальному. Но о том, как рассчитывается вектор $\vec{w}$ , мы еще узнаем в 5-м разделе статьи. А пока возвращаемся на землю обетованную — к нашему банкиру и трем его клиентам.

Благодаря функции $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ мы знаем кому можно дать кредит, а кому нужно отказать. Но с такой информацией к директору идти нельзя, ведь от нас хотели получить вероятность возврата кредита каждым заемщиком. Что делать? Ответ простой — нам нужно как-то преобразовать функцию $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ , значения которой лежат в диапазоне $(-\infty,+\infty)$ на функцию, значения которой будут лежать в диапазоне $[0,1]$ . И такая функция существует, ее называют функцией логистического отклика или обратного-логит преобразования. Знакомьтесь:

$\sigma(\vec{w}^T \vec{x_i}) = \frac{1}{1+e^{-\vec{w}^T \vec{x_i}}}$

Посмотрим по шагам как получается функция логистического отклика. Отметим, что шагать мы будем в обратную сторону, т.е. мы предположим, что нам известно значение вероятности, которое лежит в пределах от $0$ до $1$ и далее мы будем «раскручивать» это значение на всю область чисел от $-\infty$ до $+\infty$ .

03. Выводим функцию логистического отклика

Шаг 1. Переведем значения вероятности в диапазон $[0,+\infty)$

На время трансформации функции $f(w,x_i) = w_0 + w_1x_{i1} + w_2x_{i2}$ в функцию логистического отклика $\sigma(\vec{w}^T \vec{x_i}) = \frac{1}{1+e^{\vec{w}^T \vec{x_i}}}$ мы оставим в покое нашего кредитного аналитика, а вместо этого пройдемся по букмекерским конторам. Нет, конечно, ставки делать мы не будем, все что нас там интересует, так это смысл выражения, например, шанс 4 к 1. Шансы, знакомые всем делающим ставки игрокам, являются соотношением «успехов» к «неуспехам». С точки зрения вероятностей, шансы — это вероятность наступления события, деленная на вероятность того, что событие не произойдет. Запишем формулу шанса наступления события $(odds_+)$ :

$odds_+ = \frac{p_+}{1-p_+}$

, где $p_+$ — вероятность наступления события, $(1-p_+)$ — вероятность НЕ наступления события

Например, если вероятность того, что молодой, сильный и резвый конь по прозвищу «Ветерок» обойдет на скачках старую и дряблую старушку по кличке «Матильда» равняется $0.8$ , то шансы на успех «Ветерка» составят $4$ к $1$ $(0.8/(1-0.8))$ и наоборот, зная шансы, нам не составит труда вычислить вероятность $p_+$ :

$\frac{p_+}{1-p_+} = 4 \mkern 15mu \Longrightarrow \mkern 15mu p_+=4(1-p_+) \mkern 15mu \Longrightarrow \mkern 15mu 5p_+=4 \mkern 15mu \Longrightarrow \mkern 15mu p_+=0.8$

Таким образом, мы научились «переводить» вероятность в шансы, которые принимают значения от $0$ до $+\infty$ . Сделаем еще один шаг и научимся «переводить» вероятность на всю числовую прямую от $-\infty$ до $+\infty$ .

Шаг 2. Переведем значения вероятности в диапазон $(-\infty,+\infty)$

Шаг этот очень простой — прологарифмируем шансы по основанию числа Эйлера $e$ и получим:

$f(w,x_i)=\vec{w}^T\vec{x}=ln(odds_+)$

Теперь мы знаем, что если $p_+=0.8$ , то вычислить значение $f(w,x_i)$ будет очень просто и, более того, оно должно быть положительным: $f(w,x_i)=ln(odds_+)=ln(0.8/0.2)=ln(4) \approx +1.38629$ . Так и есть.

Ради любопытства проверим, что если $p_+=0.2$ , тогда мы ожидаем увидеть отрицательное значение $f(w,x_i)$ . Проверяем: $f(w,x_i)=ln(0.2/0.8)=ln(0.25) \approx -1.38629$ . Все верно.

Теперь мы знаем как перевести значение вероятности от $0$ до $1$ на всю числовую прямую от $-\infty$ до $+\infty$ . В следующем шаге сделаем все наоборот.

А пока, отметим, что в соответствии с правилами логарифмирования, зная значение функции $f(w,x_i)$ , можно вычислить шансы:

$odds_+ = e^{f(w,x_i)} = e^{\vec{w}^T\vec{x}}$

Этот способ определения шансов нам пригодится на следующем шаге.

Шаг 3. Выведем формулу для определения

Итак, мы научились, зная $p_+$ , находить значения функции $f(w,x_i)$ . Однако, на самом деле нам нужно все с точностью до наоборот — зная значение находить $p_+$ . Для этого обратимся к такому понятию как обратная функция шансов, в соответствии с которой:

$p_+ = \frac{odds_+}{1+odds_+}$

В статье мы не будем выводить вышеобозначенную формулу, но проверим на цифрах из примера выше. Мы знаем, что при шансах равными 4 к 1 ( $odds_+=4$ ), вероятность наступления события равна 0.8 ( $p_+=0.8$ ). Сделаем подстановку: $p_+=\frac{4}{1+4}=0.8$ . Это совпадает с нашими вычислениями, проведенными ранее. Двигаемся далее.

На прошлом шаге мы вывели, что $odds_+ = e^{\vec{w}^T\vec{x}}$ , а значит можно сделать замену в обратной функции шансов. Получим:

$p_+ = \frac{e^{\vec{w}^T\vec{x}}}{1+e^{\vec{w}^T\vec{x}}}$

Разделим и числитель и знаменатель на $e^{\vec{w}^T\vec{x}}$ , тогда:

$p_+ = \frac{1}{1+e^{-\vec{w}^T\vec{x}}} = \sigma(\vec{w}^T\vec{x})$

На всякий пожарный, дабы убедиться, что мы нигде не ошиблись, сделаем еще одну небольшую проверку. На шаге 2, мы для $p_+=0.8$ определили, что $f(w,x_i) \approx +1.38629$ . Тогда, подставив значение $f(w,x_i)$ в функцию логистического отклика, мы ожидаем получить . Подставляем и получаем: $p_+=\frac{1}{1+e^{-1.38629}}=0.8$

Поздравляю вас, уважаемый читатель, мы только что вывели и протестировали функцию логистического отклика. Давайте посмотрим на график функции.

График 3 «Функция логистического отклика»

Код для отрисовки графика

import math

def logit (f):
    return 1/(1+math.exp(-f))

f = np.arange(-7,7,0.05)
p = []

for i in f:
    p.append(logit(i))

fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$')
plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16)
plt.ylabel('$p_{i+}$', size = 16)
plt.legend(prop = {'size': 14})
plt.show()

В литературе также можно встретить название данной функции как сигмойд-функция. По графику хорошо заметно, что основное изменение вероятности принадлежности объекта к классу происходит на относительно небольшом диапазоне $f(w,x_i)$ , где-то от $-4$ до $+4$ .

Предлагаю вернуться к нашему кредитному аналитику и помочь ему с вычислением вероятности погашения кредитов, иначе он рискует остаться без премии :)

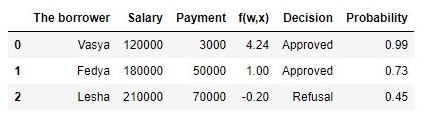
Таблица 2 «Потенциальные заемщики»

Код для формирования таблицы

proba = []
for i in df['f(w,x)']:
    proba.append(round(logit(i),2))
    
df['Probability'] = proba

df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]

Итак, вероятность возврата кредита мы определили. В целом, это похоже на правду. Действительно, вероятность того что Вася при зарплате в 120.000Р сможет ежемесячно отдавать в банк 3.000Р близка к 100%. Кстати, мы должны понимать, что банк может выдать кредит и Леше в том случае, если политикой банка предусмотрено, например, кредитовать клиентов с вероятностью возврата кредита более, ну скажем, 0.3. Просто в таком случае банк сформирует больший резерв под возможные потери.

Также следует отметить, что соотношение зарплаты к платежу не менее 3 и с запасом в 5.000Р было взято с потолка. Поэтому нам нельзя было использовать в первоначальном виде вектор весов $\vec w = (-5000,1,-3)$ . Нам требовалось сильно уменьшить коэффициенты и в таком случае мы разделили каждый коэффициент на 25.000, то есть по сути мы подогнали результат. Но это сделано было специально, чтобы упростить понимание материала на начальном этапе. В жизни, же нам потребуется не выдумывать и подгонять коэффициенты, а находить их. Как раз в следующих разделах статьи мы выведем уравнения, с помощью которых подбираются параметры $\vec{w}$ .

04. Метод наименьших квадратов при определении вектора весов $\vec{w}$ в функции логистического отклика

Нам уже известен такой метод подбора вектора весов $\vec{w}$ , как метод наименьших квадратов (МНК) и собственно, почему бы нам тогда не использовать его в задачах бинарной классификации? Действительно, ничто не мешает использовать МНК, только вот данный способ в задачах классификации дает результаты менее точные, нежели Logistic Loss. Этому есть теоретическое обоснование. Давайте для начала посмотрим на один простой пример.

Предположим, что наши модели (использующие MSE и Logistic Loss) уже начали подбор вектора весов $\vec{w}$ и мы остановили расчет на каком-то шаге. Неважно, в середине, в конце или в начале, главное, что у нас уже есть какие-то значения вектора весов и допустим, что на этом шаге, вектора весов $\vec{w}$ для обеих моделей не имеют различий. Тогда возьмем полученные веса и подставим их в функцию логистического отклика ( $\frac{1}{1+e^{-\vec{w}^T\vec{x}}}$ ) для какого-нибудь объекта, который относится к классу $+1$ . Исследуем два случая, когда в соответствии с подобранным вектором весов наша модель сильно ошибается и наоборот — модель сильно уверена в том, что объект относится к классу $+1$ . Посмотрим какие штрафы будут «выписаны» при использовании МНК и Logistic Loss.

Код для расчета штрафов в зависимости от используемой функции потерь

# класс объекта
y = 1
# вероятность отнесения объекта к классу в соответствии с параметрами w
proba_1 = 0.01

MSE_1 = (y - proba_1)**2
print 'Штраф MSE при грубой ошибке =', MSE_1

# напишем функцию для вычисления f(w,x) при известной вероятности отнесения объекта к классу +1 (f(w,x)=ln(odds+))
def f_w_x(proba):
    return math.log(proba/(1-proba)) 

LogLoss_1 = math.log(1+math.exp(-y*f_w_x(proba_1)))
print 'Штраф Log Loss при грубой ошибке =', LogLoss_1

proba_2 = 0.99

MSE_2 = (y - proba_2)**2
LogLoss_2 = math.log(1+math.exp(-y*f_w_x(proba_2)))

print '**************************************************************'
print 'Штраф MSE при сильной уверенности =', MSE_2
print 'Штраф Log Loss при сильной уверенности =', LogLoss_2

Случай с грубой ошибкой — модель относит объект к классу $+1$ с вероятностью в 0,01

Штраф при использовании МНК составит:
$MSE = (y - p_+) = (1-0.01)^2 = 0.9801$

Штраф при использовании Logistic Loss составит:
$Log Loss = log_e(1+e^{-yf(w,x)}) = log_e(1+e^{-1(-4.595...)}) \approx 4.605$

Случай с сильной уверенностью — модель относит объект к классу $+1$ с вероятностью в 0,99

Штраф при использовании МНК составит:
$MSE = (1-0.99)^2 = 0.0001$

Штраф при использовании Logistic Loss составит:
$Log Loss = log_e(1+e^{-4.595...}) \approx 0.01$

Этот пример хорошо иллюстрирует, что при грубой ошибке функция потерь Log Loss штрафует модель значительно сильнее, чем MSE. Давайте теперь разберемся, каковы теоретические предпосылки использования функции потерь Log Loss в задачах классификации.

05. Метод максимального правдоподобия и логистическая регрессия

Как и было обещано в начале, статья изобилует простыми примерами. В студии очередной пример и старые гости — заемщики банка: Вася, Федя и Леша.

На всякий пожарный, перед тем как развивать пример, напомню, что в жизни мы имеем дело с обучающей выборкой из тысяч или миллионов объектов с десятками или сотнями признаков. Однако здесь цифры взяты так, чтобы они легко укладывались в голове начинающего датасайнтеста.

Возвращаемся к примеру. Представим, что директор банка решил выдать кредит всем нуждающимся, несмотря на то, что алгоритм подсказывал не выдавать его Леше. И вот прошло достаточно времени и нам стало известно кто из трех героев погасил кредит, а кто нет. Что и следовало ожидать: Вася и Федя погасили кредит, а Леша — нет. Теперь давайте представим, что этот результат будет для нас новой обучающей выборкой и, при этом у нас как будто исчезли все данные о факторах, влияющих на вероятность погашения кредита (зарплата заемщика, размер ежемесячного платежа). Тогда интуитивно мы можем полагать, что каждый третий заемщик не возвращает банку кредит или другими словами вероятность возврата кредита следующим заемщиком $p=\frac{2}{3}$ . Этому интуитивному предположению есть теоретическое подтверждение и основывается оно на методе максимального правдоподобия, часто в литературе его называют принципом максимального правдоподобия.

Для начала познакомимся с понятийным аппаратом.

Правдоподобие выборки — это вероятность получения именно такой выборки, получения именно таких наблюдений / результатов, т.е. произведение вероятностей получения каждого из результатов выборки (например, погашен или не погашен кредит Васей, Федей и Лешей одновременно).

Функция правдоподобия связывает правдоподобие выборки со значениями параметров распределения.

В нашем случае, обучающая выборка представляет собой обобщённую схему Бернулли, в которой случайная величина принимает всего два значения: $1$ или $0$ . Следовательно, правдоподобие выборки можно записать как функцию правдоподобия от параметра $p$ следующим образом:

$P(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p) = \prod\limits_{i=1}^3 p^{y_i} (1-p)^{(1-y_i)} \mkern 5mu = \mkern 5mu p^1(1-p)^{1-1} \centerdot p^1(1-p)^{1-1} \centerdot p^0(1-p)^{1-0} \mkern 5mu =$
$= \mkern 5mu p \centerdot p \centerdot (1-p) \mkern 5mu = \mkern 5mu p^2(1-p)$

Вышеуказанную запись можно интерпретировать так. Совместная вероятность того, что Вася и Федя погасят кредит равна $p \centerdot p = p^2$ , вероятность того что Леша НЕ погасит кредит равна $1-p$ (так как имело место именно НЕ погашение кредита), следовательно совместная вероятность всех трех событий равна $p^2(1-p)$ .

Метод максимального правдоподобия — это метод оценки неизвестного параметра путём максимизации функции правдоподобия. В нашем случае требуется найти такое значение $p$ , при котором $P(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p) = p^2(1-p)$ достигает максимума.

Откуда собственно идея — искать значение неизвестного параметра, при котором функция правдоподобия достигает максимума? Истоки идеи проистекают из представления о том, что выборка — это единственный, доступный нам, источник знания о генеральной совокупности. Все, что нам известно о генеральной совокупности, представлено в выборке. Поэтому, все, что мы можем сказать, так это то, что выборка — это наиболее точное отражение генеральной совокупности, доступное нам. Следовательно, нам требуется найти такой параметр, при котором имеющаяся выборка становится наиболее вероятной.

Очевидно, мы имеем дело с оптимизационной задачей, в которой требуется найти точку экстремума функции. Для нахождения точки экстремума необходимо рассмотреть условие первого порядка, то есть приравнять производную функции к нулю и решить уравнение относительно искомого параметра. Однако поиски производной произведения большого количества множителей могут оказаться делом затяжным, чтобы этого избежать существует специальный прием — переход к логарифму функции правдоподобия. Почему возможен такой переход? Обратим внимание на то, что мы ищем не сам экстремум функции $P(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p)$ , а точку экстремума, то есть то значение неизвестного параметра $p$ , при котором $P(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p)$ достигает максимума. При переходе к логарифму точка экстремума не меняется (хотя сам экстремум будет отличаться), так как логарифм — монотонная функция.

Давайте, в соответствии с вышеизложенным, продолжим развивать наш пример с кредитами у Васи, Феди и Леши. Для начала перейдем к логарифму функции правдоподобия:

$logP(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p) \mkern 5mu = \mkern 5mu logp^2(1-p) \mkern 5mu = \mkern 5mu 2logp + log(1-p)$

Теперь мы можем с легкостью продифференцировать выражение по $p$ :

$\frac{\partial logP(\mkern 5mu \vec{y} \mkern 5mu |\mkern 5mu p)}{\partial p} \mkern 5mu = \mkern 5mu \frac{\partial}{\partial p} (2logp + log(1-p)) \mkern 5mu = \mkern 5mu \frac{2}{p} - \frac{1}{1-p}$

И наконец, рассмотрим условие перв