Отрицательный отбор кадров в иерархической структуре предприятия
Вступление
Все мы прекрасно знаем, как важен подбор персонала в организации. Но зачастую у нас достаточно смутные представления о том, как именно структура организации влияет на эффективность работы этого персонала. Или, например, как распределение сотрудников с различными параметрами в штатном расписании влияет на эффективность работы.
Когда этот вопрос поднимается, это обычно какие-то общие слова, эвристики из скучных учебников с качественными описаниями, вроде того, что иерархическая структура выдвигает вперед и мотивирует нарциссов, которые больше заинтересованы в собственном продвижении, а не благоденствии предприятия.
Оказывается, некоторые аспекты этого вопроса достаточно легко математически промоделировать, что может открывать возможности к новым вариантам управления компаниями. В условиях достаточно простых предположений о свойствах персонала огромное количество важных и интересных свойств вылезают наружу сами по себе, просто при задании структуры организации. А дальше вопрос может ставиться так — А есть ли возможность использовать это на благо организации?

Описание модели
Пошагово моделируется, как развивается большая организация , в которой каждый работающий человек на каждом уровне иерархии описывается двумя переменными и двумя подмножествами:
Где — множество,
— множество всех начальников данного человека,
— множество всех подчиненных данного человека.
— степень личной эффективности (производительности) того, как человек выполняет свои задачи на
-м уровне. На каждом уровне
, где
— равномерное распределение. Таким образом средняя личная производительность всех вместе равна 1. Тут уместно вспомнить принцип Питера, который в случае данного задания эффективностей начинает звучать так: «В иерархической системе каждый индивидуум имеет тенденцию подниматься до нижнего из уровней своей некомпетентности.» Т.е. не факт, что человек не эффективен еще выше. Просто поднимается только до того, где у него провал в эффективности. Наиболее эффективный председатель колхоза не всегда хотя бы даже сносная доярка, как мы знаем. Однако, как мы увидим дальше, что и этот принцип описывает абсолютно идеалистическую ситуацию (тем более он был справедливо раскритикован).
— степень эгоизма человека. Под эгоизмом здесь подразумевается исключительно некоторая «дистиллированная» способность делать вещи, которые не имеют отношения к производительности или выполнению рабочих функций, но по мнению человека должны способствовать его продвижению в карьере.
В модели организации генерируется человек с характеристиками описанными выше, которые изначально случайно распределяются по
уровням. Вместимость каждого уровня задается из следующих соображений:
Нам всем известен анекдот про математиков, которые заказывают пиво в баре, прося каждый раз половину от того, что просил предыдущий:
Таким образом, для -го уровня количество людей на уровне может рассчитываться по следующей формуле:
где — округление вниз (floor).
— нормировочная сумма, чтобы в финале получилось ровно
человек.
Соответственно, полностью организация задается как вектор размерности
, где
-й уровень задается множеством сотрудников
Каждый человек имеет набор начальников (кроме верхнего уровня) и набор подчиненных (кроме нижнего уровня) — . Чтобы задать для каждого человека этот список, мы пользуемся таким алгоритмом:
Пусть задана организация . Тогда для каждого человека
, также принадлежащего
, список
из
подчиненных задается так:
H.D=[]
if H.i != 0:
H.D = random.shuffle(O[i-1])[:K]
for dependant in H.D:
dependant.C.append(H)
Получается граф, расширяющейся с верха иерархии в духе дерева, но не дерево, потому что между двумя вершинами может быть более одного пути.
На каждой итерации производительность каждого человека считается по следующей формуле:
где — множество производительностей всех подчиненных. Суть этой формулы, что эгоизм отдельных подчиненных нивелируется их количеством
, при этом общая производительность системы без учета эгоизма это производительность самого слабого звена в подчинения
.
Далее на каждой итерации считается производительность у всех людей:
В качестве основной меры эффективности структуры используется производительность нормированная на количество людей: . Этот показатель показывает, насколько полученный результат меньше, чем то, что должно бы было получиться в случае, если бы никто не был эгоистом и производительность каждого была бы равна 1.
В конце каждой итерации происходит этап продвижения кадров. На каждом ходу случайных человек увольняются, (уходят на пенсию или еще что-то), после чего за освободившиеся места конкурируют их прямые подчиненные, а самый низ пирамиды добавляются
уволенных с иерархией опущенной до нижнего уровня. Так делается, чтобы не вводить новые сущности и избежать дополнительных случайных блужданий результата.
Рассматривалось три модификации конкуренции:
- Сценарий с эгоистическим продвижением, когда продвижение зависит только от эгоизма сотрудника,
- Сценарий с идеалистическим продвижением, когда продвижение зависит только от производительности сотрудника на уровне смещенного начальника,
- Сценарий со смешанным продвижением, более сложная модель продвижения, описанная далее.
Сценарий с эгоистическим продвижением
Конкуренция заключается в том, что каждый прямой подчиненный уволенного имеет возможность с какой-то вероятностью участвовать в борьбе за продвижение. Победитель считается в соответствии с такой формулой:
где — вектор всех эгоизмов у подчиненных
бывшего начальника
, * — поэлементное умножение,
— вектор случайных значений из
размерности
.
Сценарий с идеалистическим продвижением
Победитель считается в соответствии с такой формулой:
где — вектор всех потенциальных производительностей у подчиненных
для
-го уровня бывшего начальника
.
Сценарий со смешанным продвижением
Было предложено взять модель конкуренции принятую в одной из развитых стран. «Пирамида делится на две половины. Снизу продвижение коррелирует с производительностью. Сверху продвижение определяется произведением эгоизма и суммарной производительности по всей цепочке вниз. Переход из нижней половины в верхнюю — чистый эгоизм.»
Реализовано это может быть так:
prob = []
center = round(L/2)
for D in H.D:
if D.i
Функция Col (D), это рекуррентная функция, которая суммирует производительности всех подлежащих подчиненных:
def Col(H):
result = 0
for D in H.D:
result += D.P + Col(D)
return result
Что получается при симуляции?
Сценарий с эгоистическим продвижением
Рассмотрим результат расчета по сценарию с эгоистическим продвижением, где «проживается» 60 итераций для популяции 10000 человек. Первый график, это то, как меняется с годами производительность. Тут стоит отметить, что значение 1 нем было бы только если бы все сотрудники имели идеальную эффективность на всех уровнях. А второй, это то, как с годами меняется распределение эгоистов (можно заметить, что изначально всего эгоистов на уровне 20% от всей популяции уровня, что как бы достаточно оптимистично).

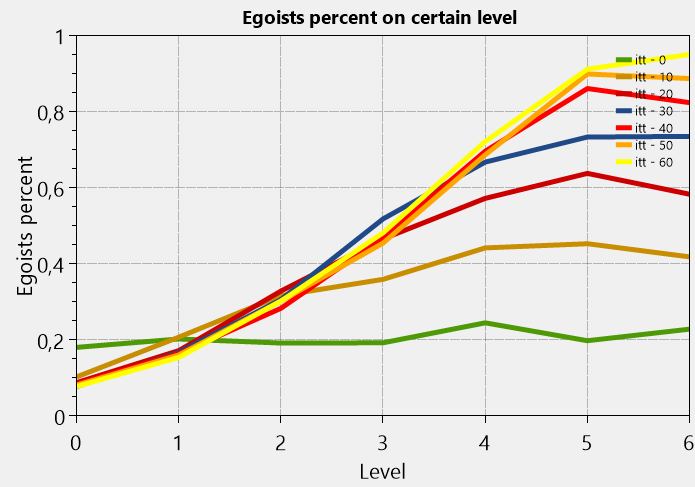
Продуктивность падает более чем в два раза. Количество эгоистов на верхних уровнях растет, экспоненциально стремясь к полному заполнению верхних уровней.
Ну и очевидный вывод — количество эгоистов на верхних уровнях растет, а производительность падает, потому что эгоизм не всегда сочетается с хорошей производительностью. Кто бы сомневался.
Сценарий с идеалистическим продвижением
Все те же параметры. 10000 человек, 60 итераций, 20% эгоистов на любом уровне в начале. В коде изменена одна строка. Критерий по которому производится конкуренция за места. Вместо эгоизма теперь уровень потенциальной производительности на уровне смещенного начальника. В частном случае получается вот так.
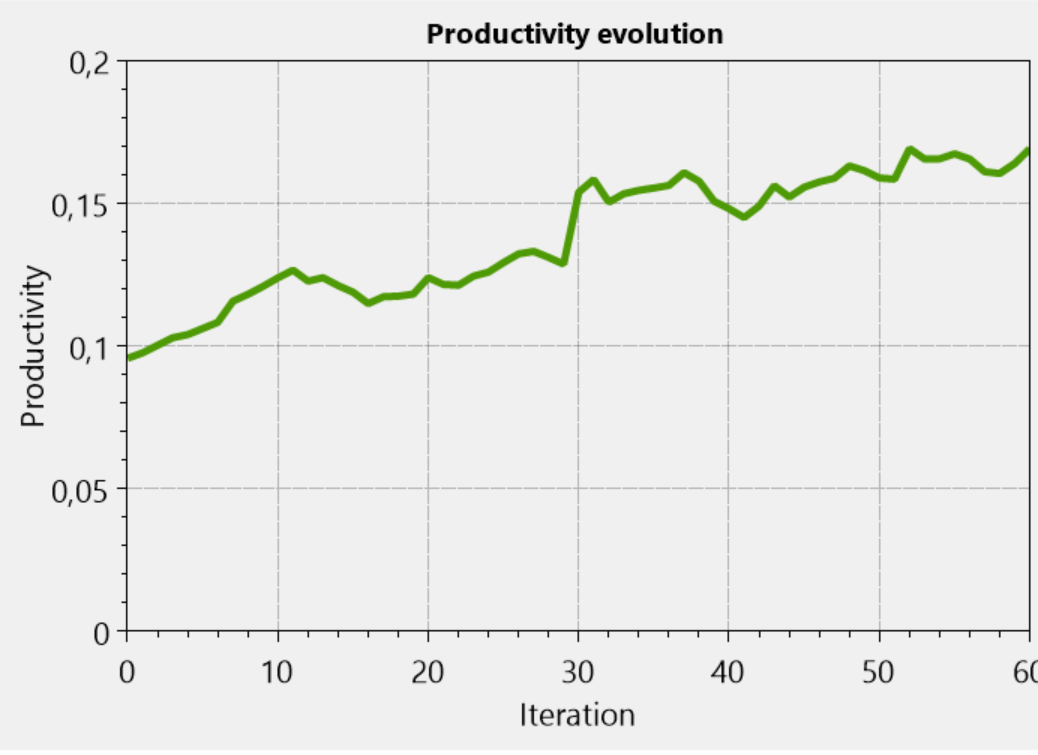

Так как уровень эгоизма не коррелирован никак с уровнем производительности, то перераспределение производительных людей в верхние уровни никак на эгоизме этого уровня не сказывается. Но при этом производительность всех растет за счет продвижения талантливых.
Сценарий со смешанным продвижением
Параметры те же. Только другое правило. Сложная схема разделения оценки разных уровней иерархии.

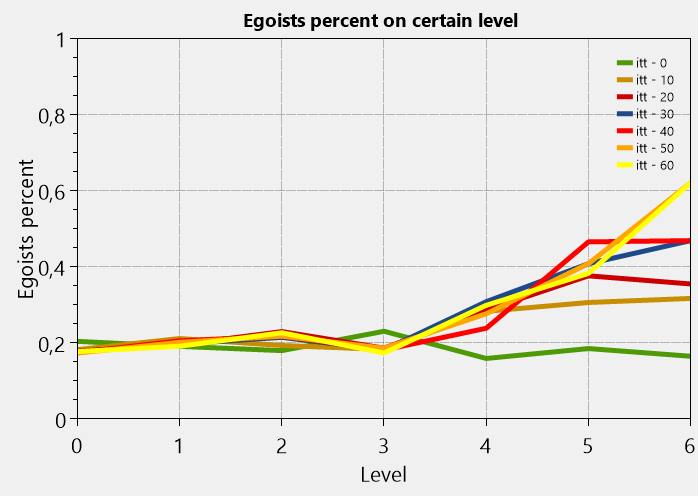
Как видно, в такой организации количество эгоистов в правлении тоже растет, но не до таких вопиющих значений как в эгоистичном сценарии. Более того, процесс сходится не к 1 на высшем уровне. Соответственно, падение производительности от засилья эгоизма существенно ниже. До 0.06, а не до 0.04, как в эгоистичном варианте.
Обобщения и доверительные интервалы
Может возникнуть некоторое количество вопросов о том, как именно эти графики могут варьироваться, в зависимости от разных реализаций случайного процесса. Может и нет никакой такой большой разницы между эгоизмом и смешанным вариантом? Просто две максимально различные реализации.
Для этого каждый из сценариев был прогнан 20 раз с одними и теми же параметрами. После этого построены графики с доверительными интервалами для среднего каждого процесса. Результаты на графике.
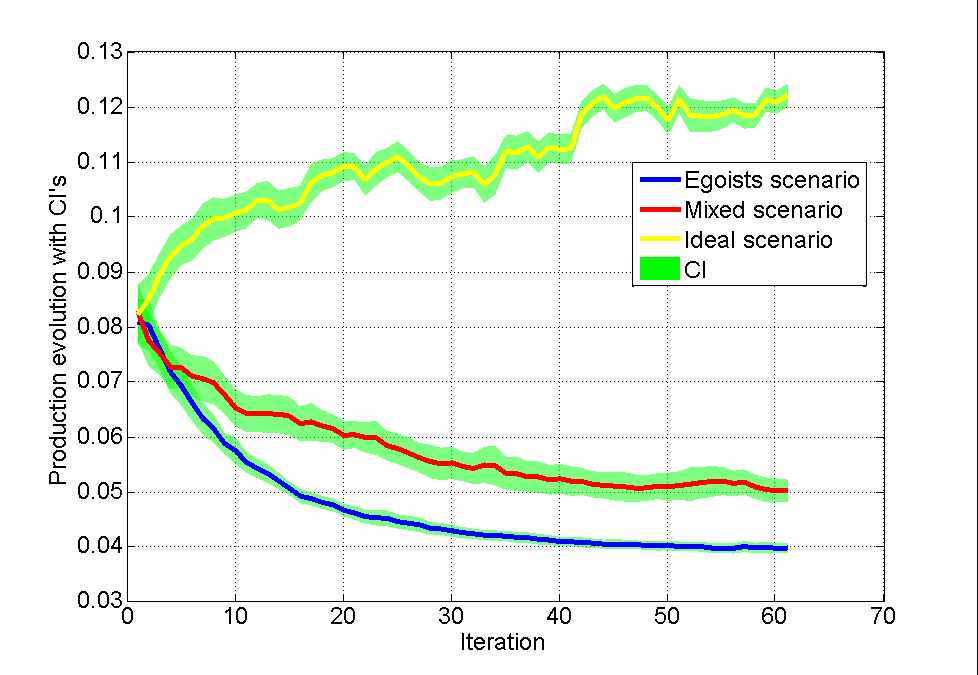
Можно отметить некоторое количество интересных особенностей этих зависимостей.
Доверительные интервалы для эгоистичного сценария уже, чем в остальных случаях. Так происходит потому, что процесс после второй итерации получается достаточно гомогенный. Некоторое значительное число людей со случайными характеристиками производительности попадут на более высокий уровень, чем будут обеспечивать снижение производительности всем своим подчиненным. Это происходит потому, что они с одной стороны достаточно эгоистичны, чтобы пробиться еще выше, чем они были. С другой, в графе достаточно широкая разветвленность и связность сетки подчинения, которая будет создавать ситуацию, когда эгоисты будут иметь большую вероятность попасть в какой-то из «конкурсов» на новое место выше в иерархии. И с каждым уровнем эта вероятность все больше и больше, пока верхний уровень не заполнится самыми отчаянными эгоистами. В этот момент процесс начнет сходиться.
Причина широкого доверительного интервала смешанного варианта объясняется (по большей части) тем, что для этой структуры ротация кадров на высших уровнях достаточно быстро «скидывает» эгоистов, которые порождают неэффективные цепочки производства. Человек эгоистично дошел до верхнего уровня и ничто ему не мешало, а там вдруг (после очередного повышения) его решения делают неэффективным работу огромного количества подчиненных. И на следующей же итерации этот человек не выигрывает продвижение относительно более продуктивного соперника. А когда это происходит, улучшение происходит достаточно скачкообразно, что можно видеть на графике с частным случаем (впрочем, иногда и понижение происходит так же). В принципе, сама схема не прям идеальна, но существенную разницу с эгоизмом мы видим.
Выводы
Неконтролируемое продвижение сотрудников может наносить предприятию существенный вред и способствовать деградации и снижению эффективности. Как показано выше, алгоритм, выбранный предприятием для ротации кадров, существенно влияет на работу всей организации.
В данной статье мы постарались дать возможность читателям посмотреть и увидеть проблему там, где ее возможно никто раньше не замечал, а также сформулировать ее в виде прикладной задачи, которая, возможно, имеет ряд адекватных решений.
Но очевидно, что идеалистическая модель с продвижением только эффективных на новом уровне сотрудников не слишком реалистична. Проблемы начинаются уже с вопроса, как понять — будет ли сотрудник эффективен на новой должности? Какие у него в ней таланты? Поэтому на данном этапе мы не вправе кидаться советами, как оптимизировать ситуацию. Перенос модельных реализаций на конкретную реальную структуру это всегда вещь крайне деликатная и требующая изрядного количества практических проверок и доказательств эффективности такого переноса.
Однако, напоследок уместно будет вспомнить, что в 2010 году шнобелевскую премию дали исследователям из Италии, которые, воспользовавшись принципом Питера, доказали, что наиболее эффективным алгоритмом продвижения (в случае, если этот принцип адекватен реальности) было бы продвижение случайного сотрудника, выбранного генератором случайных чисел. Уж совсем случайного, наверное, не стоит, но, возможно, было бы всем полезнее выбирать случайного из шорт-листа. Но это не точно.
Автор статьи: Александр Беспалов, Data scientist, Maxilect
P.S. Мы публикуем наши статьи на нескольких площадках рунета. Подписывайтесь на наши страницы в VK, FB или Telegram-канал, чтобы узнавать о всех наших публикациях и других новостях компании Maxilect.
