Основы моделирования в openEMS
В прошлой части было рассказано как установить и настроить open-source электромагнитный симулятор openEMS. Теперь можно переходить к моделированию. Как производить моделирование ЭМВ при помощи openEMS и Octave будет рассказано в этой статье.Мы будем моделировать процесс распространения электромагнитной волны (ЭМВ) между двумя параллельными металлическим пластинами.
Конфигурация объекта показана на рисунке. Предполагается прямоугольный источник ЭМВ, от которого ЭМВ распространяется в обе стороны.
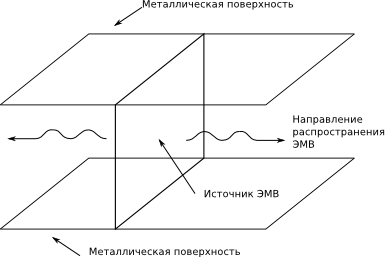
Под катом приведён построчный разбор скрипта для моделирования такого объекта.Как было сказано в предыдущей части, все симуляции в openEMS являются скриптами Octave/Matlab. Запускаем Octave/Matlab и вводим следующие команды. Сначала инициализируем пространство. Мы создаём специальный объект FDTD, который описывает пространство конечной разности во временной области:
FDTD = InitFDTD ('NrTS',100,'EndCriteria',0,'OverSampling',50); Параметры функции — это 100 точек расчёта по времени от нуля. Шаг расчёта по времени выбирается автоматически на основе частоты Найквиста и частоты источника ЭМВ. Попробуйте задать другое количество точек, например 1000.
Теперь устанавливаем источник ЭМВ частотой 10 МГц. Здесь параметры функции понятны из названия.
FDTD = SetSinusExcite (FDTD,10e6); Для любого моделирования ЭМВ нужны граничные условия. Граничные условия описывают свойства материала, которым ограничено пространств в направлении каждой из трёх осей координат X, Y, Z. Порядок следования граничных условий в параметрах функции следующий X+, X-, Y+, Y-, Z+, Z- У нас пространство по оси Y в положительном направлении ограничено идеально проводящей поверхностью (PEC — Perfect Electric Conductor), в отрицательном направлении по Y — также проводящей поверхностью. PMC — это идеальныймагнитопроводник. MUR — это абсолютно поглощающий диэлектрик. Он приблизительно соответствует материалу стенок безэховой камеры.
FDTD = SetBoundaryCond (FDTD,{'PMC' 'PMC' 'PEC' 'PEC' 'MUR' 'MUR'}); Ещё доступен специальный многослойный материал (PML_x) для граничных условий. Он может иметь от 6 до 20 слоёв (например PML_8, PML_10). Этот материал тоже действует как поглощающий диэлектрик.
После того как заданы граничные условия инициализируем пространство CSX, в котором будет задана геометрия нашей системы.
CSX = InitCSX (); Теперь нужно создать сетку. Расчёт распространения ЭМВ будет выполняться внутри пространства, ограниченного сеткой. Сначала задаём размерность сетки по координатам (X*Y*Z=20×20*40 метров).
mesh.x = -10:10; mesh.y = -10:10; mesh.z = -10:30; Теперь создаём собственно сетку в прямоугольных координатах при помощи функцииDefineRectGrid () и применяем её к геометрии (шаг сетки равен 1 метру):
CSX = DefineRectGrid (CSX,1, mesh); Далее создаём источник ЭМВ. Задаём амплитуду ЭМВ и направление вектора ЭМВ. Для этого служит функция AddExcitation.octave:16> CSX = AddExcitation (CSX,'excitation',0,[0 1 0]);
Первый и второй параметры функции — это имя CSX-пространства и имя источника ЭМВ соответственно. Третий параметр функции — это тип поля. Доступны следующие типы:
0 — электрическое поле (Е), жёсткое возбуждение 1 — электрическое поле (Е), жёсткое возбуждение 2 — магнитное поле (Н), мягкое возбуждение 3 — магнитное поле (Р), жёсткое возбуждение 10 — плоская ЭМВ Отличие жёсткого и мягкого возбуждения состоит в том, что при жёстком возбуждении амплитуда ЭМВ в данной точке пространства устанавливается принудительно заданному значению, а при мягком возбуждении рассчитывается суперпозиция полей, то есть ЭМВ накладывается на имеющиеся в данной точке пространства поля.Четвёртый параметр — это вектор, компоненты которого задают амплитуду ЭМВ по трём направлениям X, Y, Z.
Таким образом мы задали возбуждение электрическим полем амплитудой 1 В/м в направлении оси Y.
Теперь создаём площадку (AddBox) с которой будем распространяться ЭМВ. Эта площадка и является собственно источником ЭМВ.
CSX = AddBox (CSX,'excitation',0,[-10 -10 0],[10 10 0]); На этом описание геометрии завершено. После того как мы описали геометрию, нужно создать сечение, в котором мы будем наблюдать распространение ЭМВ. Это делается при помощи функций AddDump () и AddBox ().
CSX = AddDump (CSX,'Et'); CSX = AddBox (CSX,'Et',0,[-10 0 -10],[10 0 30]); Теперь подготавливаем временный каталог для хранения результатов расчётов и просматриваем геометрию при помощи CSXCAD.
mkdir ('tmp'); WriteOpenEMS ('/tmp/tmp.xml', FDTD, CSX); CSXGeomPlot ('/tmp/tmp.xml'); invoking AppCSXCAD, exit to continue script… QCSXCAD — disabling editing Всё, модель нашей структуры готова. Можно запускать симулятор. Если всё нормально, то мы увидим следующий отчёт:
RunOpenEMS ('tmp','/tmp/tmp.xml','');
----------------------------------------------------------------------
| openEMS 64bit — version v0.0.32–14-g63adb58
| © 2010–2013 Thorsten Liebig
Create FDTD operator (compressed SSE + multi-threading) FDTD simulation size: 21×21x41 --> 18081 FDTD cells FDTD timestep is: 1.92583e-09 s; Nyquist rate: 25 timesteps @1.03851e+07 Hz Excitation signal length is: 100 timesteps (1.92583e-07s) Max. number of timesteps: 100 (--> 1 * Excitation signal length) Create FDTD engine (compressed SSE + multi-threading) Running FDTD engine… this may take a while… grab a cup of coffee??! Time for 100 iterations with 18081 cells: 0.1624 sec Speed: 11.1336 MCells/s Симуляция завершена, и можно просмотреть результат. Запускаем Paraview. Затем выбираем File→Open и идём во временный каталог, где хранятся результаты симуляции. Там открываем файл Et_.vtr. Этот файл содержит информацию о результате расчёта процесса распространения ЭМВ во времени. Вот, что нужно открывать, путь к файлу у вас будет другой:
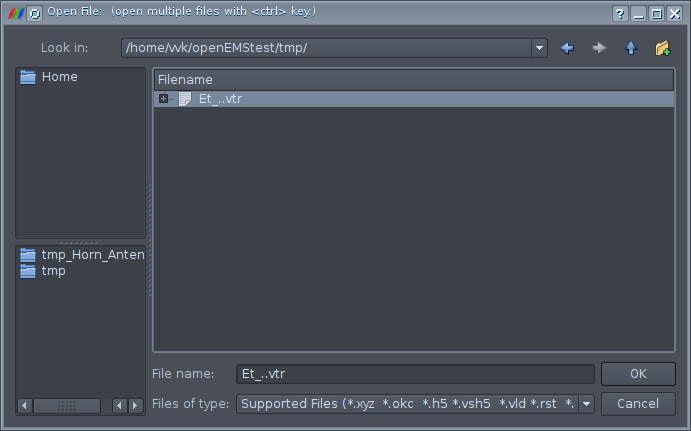
Теперь видим в окне Paraview плоскость, которая является сечением в котором мы смотрим амплитуду ЭМВ.

Чтобы визуализировать амплитуду ЭМВ, нужно в выпадающем списке Coloring выбрать E-field (по умолчанию там стоит SolidColor) и затем отобразить цветовую легенду (нажать Show). Теперь мы видим амплитуду ЭМВ в момент времени t=0. В начальный момент времени амплитуда ЭМВ тоже равна нулю во всём пространстве, поэтому вся плоскость будет закрашена в один цвет. Чтобы посмотреть распределение ЭМВ нужно установить время отличное от нуля и нажать кнопку Rescale. Теперь на плоскости отобразится распределение амплитуды ЭМВ.
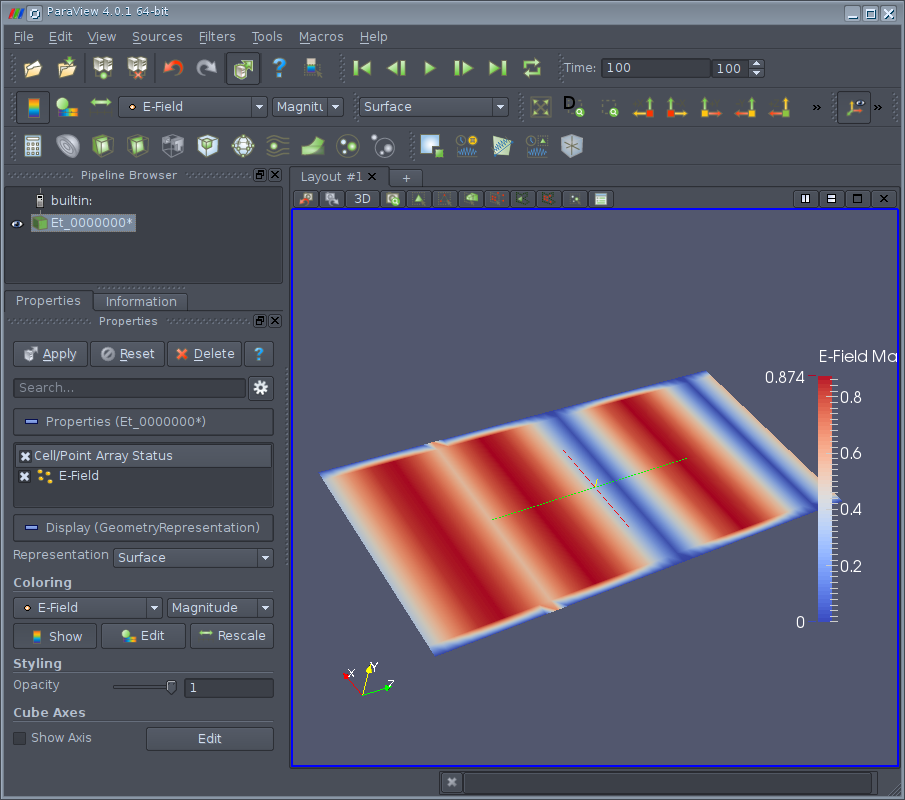
Можно также запустить анимацию и просмотреть процесс распространения ЭМВ во времени. Как и следовало ожидать ЭМВ распространяется в обоих направлениях от плоскости-источника.
В результате мы смоделировали во временной области процесс распространения ЭМВ в некоторой области пространства. В заключении скрипт Octave/Matlab целиком:
FDTD = InitFDTD ('NrTS',1000,'EndCriteria',0,'OverSampling',1); FDTD = SetSinusExcite (FDTD,10e6); FDTD = SetBoundaryCond (FDTD,{'PMC' 'PMC' 'PEC' 'PEC' 'MUR' 'MUR'}); CSX = InitCSX (); mesh.x = -10:10; mesh.y = -10:10; mesh.z = -10:30; CSX = DefineRectGrid (CSX,1, mesh); CSX = AddExcitation (CSX,'excitation',0,[0 1 0]); CSX = AddBox (CSX,'excitation',0,[-10 -10 0],[10 10 0]); CSX = AddDump (CSX,'Et'); CSX = AddBox (CSX,'Et',0,[-10 0 -10],[10 0 30]); mkdir ('tmp'); WriteOpenEMS ('/tmp/tmp.xml', FDTD, CSX); CSXGeomPlot ('/tmp/tmp.xml'); RunOpenEMS ('tmp','/tmp/tmp.xml',''); Ссылка на предыдущую статью по openEMS: habrahabr.ru/post/255317
Сайт проекта openEMS: openems.de
