Оптимизационные задачи в ритейле31.08.2022 20:31

Привет, Habr! На связи отдел аналитики данных X5 Tech.

Сегодня мы поговорим об очень интересном разделе прикладной математики — оптимизации.

Цели данной статьи:

рассказать про задачи в ритейле, которые могут решаться методами оптимизации,
продемонстрировать, как модельная задача ценообразования решается пакетами Pyomo и SciPy,
сравнить производительность солверов* Pyomo и SciPy на примере поставленной задачи.

Прим. Солвер (от англ. Solver) — программа, скомпилированная под выбранную платформу, для решения математической задачи.

Так как данная тема достаточно обширна, то помимо данной статьи (статья 1) мы планируем написать ещё две:

Статья 2: Обзор open-source солверов на примере задачи ритейла.
Статья 3: Решение модельной задачи ценообразования оптимизаторами в различных постановках.

Примеры задач

Практически каждый человек ежедневно решает оптимизационные задачи даже не задумываясь об этом. Пара примеров:

Закупка. Как правило, мы хотим минимизировать наши расходы для приобретения необходимых товаров, но при условии, чтобы эти товары были максимально полезны. Полезность здесь у каждого своя: для одних она определяется количеством растительных жиров, для других — минимальной суммарной стоимостью корзины, для третьих — наличием привычных товаров, и тд.

Отпуск. Во время ограниченного отпуска мы хотим распределить свой маршрут так, чтобы посетить всё, что запланировали с минимальными временными затратами на дорогу, и при этом не забыть позагорать на пляже.

Бизнес-требования часто приводят к задаче многокритериальной оптимизации и задаче оптимального управления. В таких постановках решения, найденные методами оптимизации, чрезвычайно полезны для принятия решений. Для иллюстрации приведём несколько задач из области ритейла, которые могут быть сформулированы в виде задачи оптимизации.

Ценообразование. Поиск оптимальной конфигурации цен с учетом ценового позиционирования, допустимых ценовых диапазонов для каждого товара и набора бизнес-ограничений. Цены должны максимизировать суммарный доход, а прибыль быть не ниже заданного уровня.

Оптимальное распределение маркетингового бюджета. Реализовать максимально эффективно выделенный на маркетинговые активности бюджет. Есть несколько каналов для рекламных акций, цель — инвестировать бюджет так, чтобы суммарный доход со всех коммуникаций был максимален. Необходимо учесть ограничения на предельную нагрузку на канал, допустимое количество коммуникаций для каждого клиента и пр.

Планирование ассортимента. Подобрать полочный ассортимент товаров так, чтобы максимизировать оборот с учетом полочного пространства и других характеристик магазина.

Закупка товаров. Задача — распределить бюджет, выделенный на закупки так, чтобы поддерживать товарооборот, заданный уровень доступности товаров и при этом достигнуть определенных финансовых показателей.

Логистика. Задача — найти оптимальный график доставки продуктов с учётом вместимости грузовиков, затрат на логистику и тд.

Общая постановка задачи и её разновидности

Прежде всего рассмотрим постановку задачи в общем виде:

— вектор размерности $x \in X$ — допустимое множество значений этих переменных.

$f(x)→\min(\max),$ $f(\cdot)$ — целевая функция;

$g_{i}(x) \leqslant 0,\ i=1..m$ — ограничения вида неравенств;

$h_i(x) = 0,\ j=1..k$ — ограничения вида равенств;

Исходя из практики можно разложить данную постановку на несколько классов в зависимости от вида целевой функции, ограничений и :

Безусловная оптимизация — отсутствуют, $X = \mathbb{R}^n$
LP (linear programming) — линейное программирование. — линейные функции, $X = \mathbb{R}_+^n$
MILP (mixed integer linear programming) — смешанное целочисленное линейное программирование, это задача LP в которой только часть переменных являются целочисленными;
NLP (nonlinear programming) — нелинейное программирование, возникает когда хотя бы одна из функций $f(x),\ g_i(x),\ h_j(x)$ нелинейна;
MINLP (mixed integer nonlinear programming) — смешанное целочисленное нелинейное программирование, возникает как и в MILP, когда часть переменных принимает целочисленные значения;

NLP в свою очередь можно подробить еще на множество разных классов в зависимости от вида нелинейности и выпуклости.

Подробнее о том, как получаются различные виды задачи ценообразования исходя из бизнес-формулировки, мы будем говорить в статье 3.

Оптимизация модельной задачи ценообразования

Рассмотрев основные классы оптимизационных задач, перейдём к построению модели ценообразования.

Предположим, что для товара известно значение эластичности E_i , а спрос задаётся следующей зависимостью:

$\begin{equation} Q_{i}(P_{i}) = Q_{0, i} \exp\bigg(E_{i} \cdot \bigg(\frac{P_{i}}{P_{0, i}} - 1\bigg)\bigg). \end{equation}$

Введём обозначения:

В качестве иллюстративного примера рассмотрим задачу с одним ограничением сложного вида и ограничения на переменные.

Задача — найти такой набор новых цен, чтобы:

максимизировать оборот со всех товаров,
общая прибыль осталась на прежнем уровне,
цены лежали в заданных границах (индекс l и u — для нижней и верхней, соответственно).

Тогда оптимизационную задачу можно записать следующей системой:

$\begin{cases} \sum_{i=1}^{n} P_i(x_i) \cdot Q_i(x_i) \to \max_{x},\\ \\ \sum_{i=1}^{n} (P_i(x_i) - C_i) \cdot Q_i(x_i) \geqslant \sum_{i=1}^{n} (P_{0, i} - C_i) \cdot Q_ {0, i},\\ \\ x_i \in [x_i^l, x_i^u], \ i=1..n\\ \end{cases}$

Данная модель принадлежит к классу NLP, как нетрудно заметить из данных выше определений.

Реализация модели в Pyomo и SciPy

Для демонстрации решения необходимы данные.

Реальные данные мы использовать не можем из-за NDA, поэтому будем генерировать их из случайных распределений (функция generate_data), исходя из наших представлений о возможных значениях величин в фуд-ритейле.

Пример данных для NLP постановки:

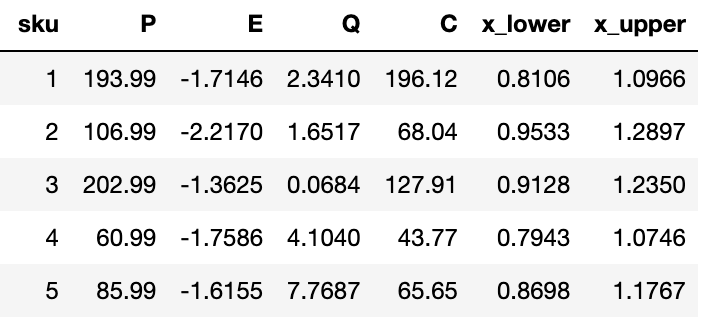
SciPy и Pyomo имеют разные интерфейсы, чтобы как-то унифицировать работу с ними, будем наследоваться от базового класса, код класса.

Методы, которые необходимо реализовать для каждого солвера:

init_objective — задание целевой функции,
init_constraints — добавление ограничений,
solve — поиск оптимального решения.

Опишем далее отличия в реализации этих методов в SciPy и Pyomo.

Другие примеры из официальной документации можно найти здесь, для Pyomo и здесь, для SciPy.

Задание целевой функции

В SciPy оптимизатор работает в режиме минимизации, поэтому суммарный оборот берём со знаком »-».

В Pyomo функцию пересчёта суммарного оборота необходимо передать в переменную expr объекта pyo.Objective.

# SciPy
def objective(x):
    return -sum(self.P * x * self.Q * self._el(self.E, x))

# Pyomo
objective = sum(self.P[i] * self.model.x[i] * self.Q[i] * self._el(i) for i in range(self.N))
self.model.obj = pyo.Objective(expr=objective, sense=pyo.maximize)

Задание ограничений

Ограничение на суммарную прибыль задаётся в методе init_constraints.

Для SciPy ограничения передаются через NonlinearConstraint или LinearConstraint ().

Для Pyomo ограничения передаются через pyo.Constraint ().

# SciPy
A = np.eye(self.N, self.N, dtype=float)
bounds = LinearConstraint(A, self.x_lower, self.x_upper)
self.constraints.append(bounds)

def con_mrg(x):
    m = sum((self.P * x - self.C) * self.Q * self._el(self.E, x))
    return m
constr = NonlinearConstraint(con_mrg, self.m_min, np.inf)
self.constraints.append(constr)

# Pyomo
self.model.x = pyo.Var(range(self.N), domain=pyo.Reals, bounds=bounds_fun, initialize=init_fun)
con_mrg_expr = sum((self.P[i] * self.model.x[i] - self.C[i]) * self.Q[i] * self._el(i)
                   for i in range(self.N)) >= self.m_min
self.model.con_mrg = pyo.Constraint(rule=con_mrg_expr)

Поиск решения

В SciPy задача оптимизации запускается через метод minimize, а в Pyomo через проинициализированный объект SolverFactory методом solve.

# SciPy
result = minimize(self.obj, self.x_init,  method='cobyla', constraints=self.constraints)

# Pyomo
solver = pyo.SolverFactory(solver, tee=False)
result = solver.solve(self.model)

Расчёт и результаты

Так как оптимизаторы устанавливаются отдельно от python, то для получения аналогичных результатов можно воспользоваться Dockerfile, настроив контейнер, как описано в README проекта.

Для сравнения расчётов достаточно выполнить команду (осторожно, в режиме compare расчёт на макбуке 2019 года занимает > 3 часов, для ускорения можно уменьшить GRID_SIZE):

python runner.py -m compare --GRID_SIZE 255

Зависимость длительности поиска оптимального решения от количества переменных представлена на графике ниже.

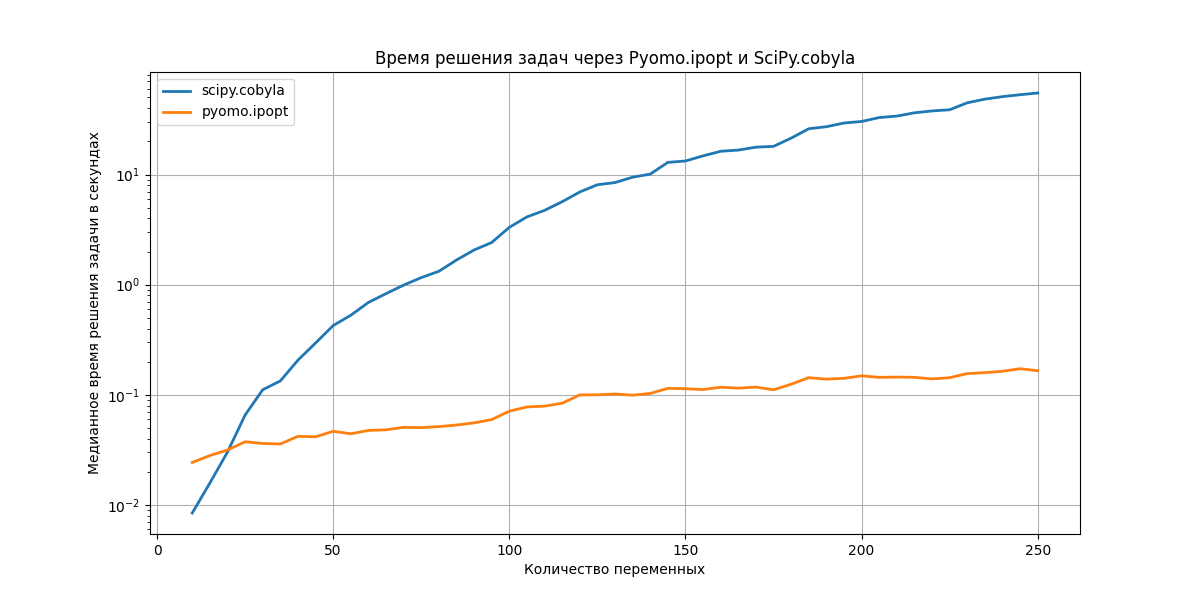
Из графика можно сделать вывод, что Pyomo с солвером ipopt значительно превосходит SciPy с cobyla при N > 20.

Отметим, что Pyomo затрачивает больше времени на подготовку данных во внутренний формат, что при небольших значениях N занимает больше времени, чем поиск решения. Более детально об этом поговорим в следующих статьях. Также затронем вопрос зависимости времени поиска решения от числа ограничений.

Заключение

В данной статье мы:

Привели типичные примеры постановок задач оптимизации в области ритейла.
Показали, как можно решать задачу ценообразования с помощью Pyomo (код для статьи).
Сравнили производительность солверов Pyomo.ipopt и Scipy.cobyla.
- Можно заметить существенную разницу во времени работы солверов и в результатах, о чем не следует забывать на практике.

В следующих статьях более детально обсудим другие open-source солверы для python, их различия в реализации и производительности.

Над статьей работали Антон Денисов, Михаил Будылин.